剑指offer——JZ68 二叉搜索树的最近公共祖先 解题思路与具体代码【C++】
一、题目描述与要求
二叉搜索树的最近公共祖先_牛客题霸_牛客网 (nowcoder.com)
题目描述
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
1.对于该题的最近的公共祖先定义:对于有根树T的两个节点p、q,最近公共祖先LCA(T,p,q)表示一个节点x,满足x是p和q的祖先且x的深度尽可能大。在这里,一个节点也可以是它自己的祖先.
2.二叉搜索树是若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值
3.所有节点的值都是唯一的。
4.p、q 为不同节点且均存在于给定的二叉搜索树中。
数据范围:
3<=节点总数<=10000
0<=节点值<=10000
如果给定以下搜索二叉树: {7,1,12,0,4,11,14,#,#,3,5},如下图:
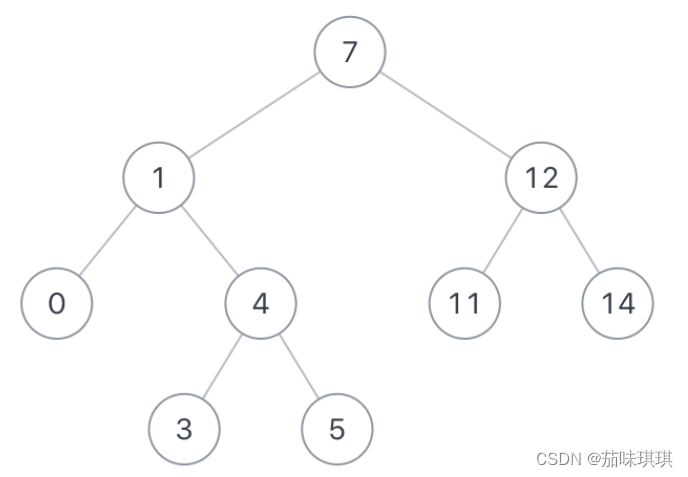
示例
示例1:
输入:{7,1,12,0,4,11,14,#,#,3,5},1,12
返回值:7
说明:节点1 和 节点12的最近公共祖先是7
示例2:
输入:{7,1,12,0,4,11,14,#,#,3,5},12,11
返回值:12
说明:因为一个节点也可以是它自己的祖先.所以输出12
二、解题思路
根据题目要求,需要我们在给定的二叉树中,找到所给出的两个结点的最近公共祖先。
思路很简单,就是我们从根节点开始分别去找到所给出的两个结点,并且记录根结点分别到两个结点的路径,然后比较这两条路径,路径中最后一个相同的结点就是两个结点最近的公共结点。其中路径的查找则可以利用二叉搜索树的性质,左子树都比根结点小,右子树都比根结点大,将所给定结点的值与根结点比较从而找到所给结点即可,路径则记录在vector中。
题目说了节点数量>=3,因此我们不需要判断树是否为空。
首先求出根结点到对应两个结点的路径;
利用for循环遍历两个路径,找到最后一个相同的结点,最后返回即可。
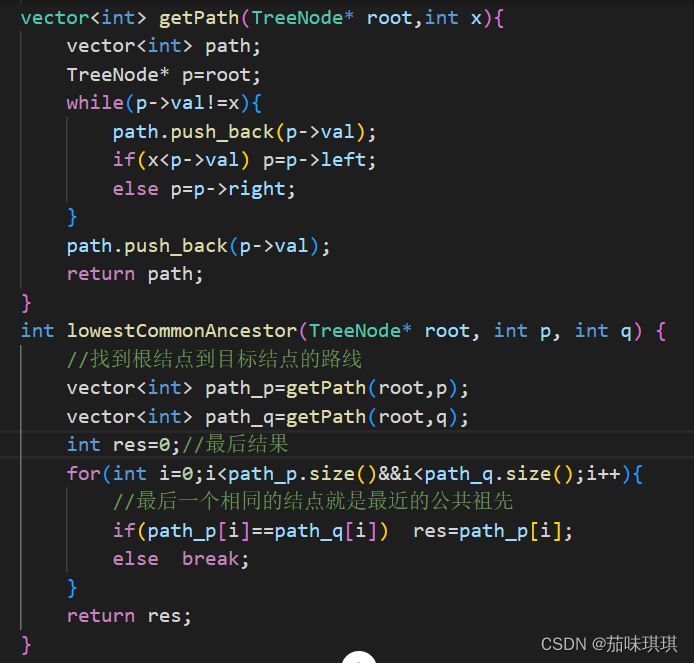
三、具体代码
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param root TreeNode类 * @param p int整型 * @param q int整型 * @return int整型*/vector<int> getPath(TreeNode* root,int x){vector<int> path;TreeNode* p=root;while(p->val!=x){path.push_back(p->val);if(x<p->val) p=p->left;else p=p->right;}path.push_back(p->val);return path;}int lowestCommonAncestor(TreeNode* root, int p, int q) {//找到根结点到目标结点的路线vector<int> path_p=getPath(root,p);vector<int> path_q=getPath(root,q);int res=0;//最后结果for(int i=0;i<path_p.size()&&i<path_q.size();i++){//最后一个相同的结点就是最近的公共祖先if(path_p[i]==path_q[i]) res=path_p[i];else break;}return res;}
};相关文章:

剑指offer——JZ68 二叉搜索树的最近公共祖先 解题思路与具体代码【C++】
一、题目描述与要求 二叉搜索树的最近公共祖先_牛客题霸_牛客网 (nowcoder.com) 题目描述 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 1.对于该题的最近的公共祖先定义:对于有根树T的两个节点p、q,最近公共祖先LCA(T,p,q)表示一个节点x&#…...

[Spring] @Bean 修饰方法时如何注入参数
目录 一、Bean 的简单使用 1、正常情况 2、问题提出 二、解决方案 1、Qualifier 2、直接写方法名 三、特殊情况 1、DataSource 一、Bean 的简单使用 在开发中,基于 XML 文件配置 Bean 对象的做法非常繁琐且不好维护,因此绝大部分情况下都是使用…...

docker拉取镜像错误 missing signature key
您正在尝试使用 yum 在 CentOS 或 RHEL 系统上安装 docker-ce,但您遇到了一些问题。根据您提供的输出,这里有几个需要注意的点: 系统未注册: "This system is not registered with an entitlement server" 指示您的系统未注册。对于…...

基于可解释性特征矩阵与稀疏采样全局特征组合的人体行为识别
论文还未发表,不细说,欢迎讨论。 Title: A New Solution to Skeleton-Based Human Action Recognition via the combination usage of explainable feature extraction and sparse sampling global features. Abstract: With the development of deep …...

OpenCV4(C++)—— 仿射变换、透射变换和极坐标变换
文章目录 一、仿射变换1. getRotationMatrix2D()2. warpAffine() 二、透射变换三、极坐标变换 一、仿射变换 在OpenCV中没有专门用于图像旋转的函数,而是通过图像的仿射变换实现图像的旋转。实现图像的旋转首先需要确定旋转角度和旋转中心,之后确定旋转…...
与Add()区别;)
http.header.Set()与Add()区别;
在Go语言中进行HTTP请求时,http.Header对象表示HTTP请求或响应的头部信息。http.Header是一个map[string][]string类型的结构,用于存储键值对,其中键表示HTTP头字段的名称,值是一个字符串切片,可以存储多个相同名称的头…...

vue-7-vuex
一、Vuex 概述 目标:明确Vuex是什么,应用场景以及优势 1.是什么 Vuex 是一个 Vue 的 状态管理工具,状态就是数据。 大白话:Vuex 是一个插件,可以帮我们管理 Vue 通用的数据 (多组件共享的数据)。例如:购…...
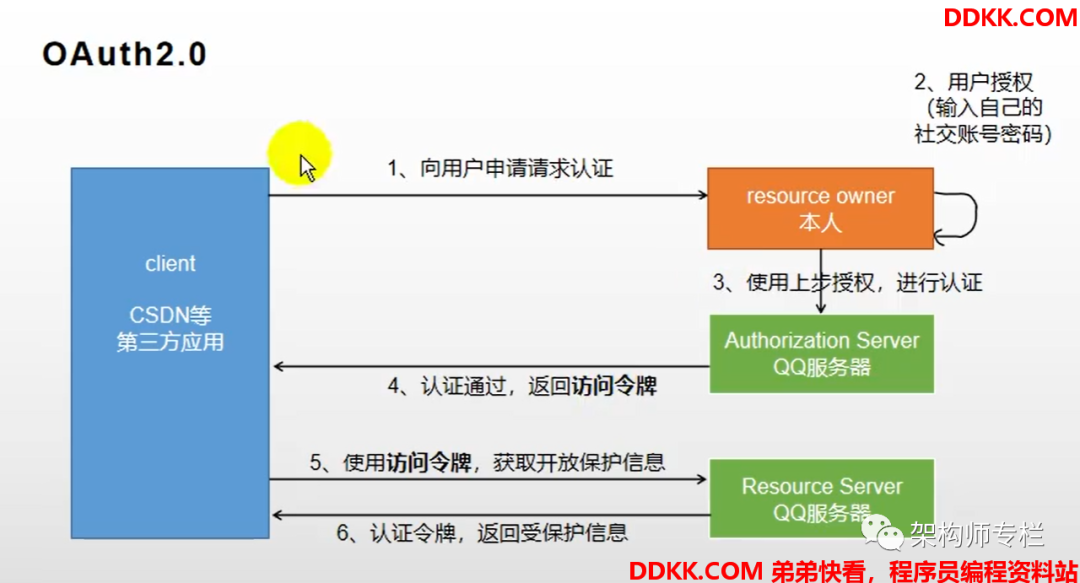
SSO单点登录和OAuth2.0区别
一、概述 SSO是Single Sign On的缩写,OAuth是Open Authority的缩写,这两者都是使用令牌的方式来代替用户密码访问应用。流程上来说他们非常相似,但概念上又十分不同。SSO大家应该比较熟悉,它将登录认证和业务系统分离,…...

【轻松玩转MacOS】基本操作篇
引言 本文是系列的开篇,我将为大家介绍MacOS的基本操作。对于初次接触MacOS的用户来说,掌握这些基本操作是必不可少的。无论是启动和关机,还是使用键盘和鼠标,或者是快捷键的使用,这些基本操作都是你开始使用MacOS的第…...

华为ICT——第三章图像处理基本任务
目录 1:数字图像处理的层次:(处理-分析-理解)顺序不能错: 2:图像处理(图像处理过程): 3:图像分析(特征提取): 4&#x…...
引用的用法总结)
(C++)引用的用法总结
引用(reference)是C极为重要的一部分,本文对其用法进行简单总结。 1. 引用的基本用法 引用的关键字为&,表示取地址的意思,引用变量定义如下: int m 1; int &n m; //定义 cout<<"n:…...

Charles:移动端抓包 / windows客户端 iOS手机 / 手机访问PC本地项目做调试
一、背景描述 1.1、本文需求:移动端进行抓包调试 1.2、理解Charles可以做什么 Charles是一款跨平台的网络代理软件,可以用于捕获和分析网络流量,对HTTP、HTTPS、HTTP/2等协议进行调试和监控。使用Charles可以帮助开发人员进行Web开发、调试…...
【AI】深度学习——人工智能、深度学习与神经网络
文章目录 0.1 如何开发一个AI系统0.2 表示学习(特征处理)0.2.1 传统特征学习特征选择过滤式包裹式 L 1 L_1 L1 正则化 特征抽取监督的特征学习无监督的特征学习 特征工程作用 0.2.2 语义鸿沟0.2.3 表示方式关联 0.2.4 表示学习对比 0.3 深度学习0.3.1 表示学习与深度学习0.3.…...
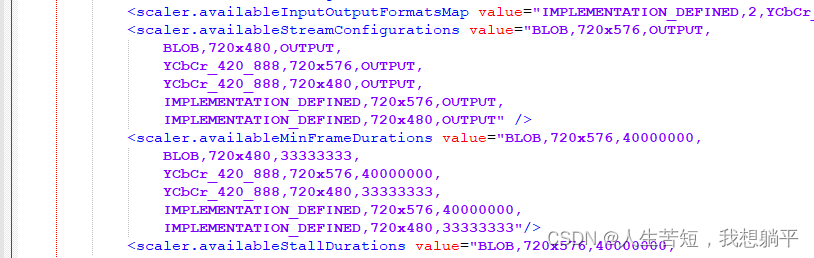
RK3288:BT656 RN6752调试
这篇文章主要想介绍一下再RK3288平台上面调试BT656 video in的注意事项。以RN6752转接芯片,android10平台为例进行介绍。 目录 1. RK3288 VIDEO INPUT 并口 2. 驱动调试 2.1 RN6752 驱动实现 ①rn6752_g_mbus_config总线相关配置 ②rn6752_querystd配置制式 …...

LLMs 蒸馏, 量化精度, 剪枝 模型优化以用于部署 Model optimizations for deployment
现在,您已经了解了如何调整和对齐大型语言模型以适应您的任务,让我们讨论一下将模型集成到应用程序中需要考虑的事项。 在这个阶段有许多重要的问题需要问。第一组问题与您的LLM在部署中的功能有关。您需要模型生成完成的速度有多快?您有多…...

Milvus踩坑笔记
本文用于记录在学习 Milvus文档时所遇到的一些Bug或报错及解决方法 参考文章: 官方demo:在Dynamic Schema的集合中插入数据 报错1:auto id enabled, id shouldnt in entities[0] 问题描述 此报错出现在Milvus官方在介绍 Dynamic Schema …...

什么是轴电流?轴电流对轴承有什么危害?
根据同步发电机结构及工作原理,由于定子铁芯组合缝、定子硅钢片接缝,定子与转子空气间隙不均匀,轴中心与磁场中心不一致等,机组的主轴不可避免地要在一个不完全对称的磁场中旋转。这样,在轴两端就会产生一个交流电压。…...
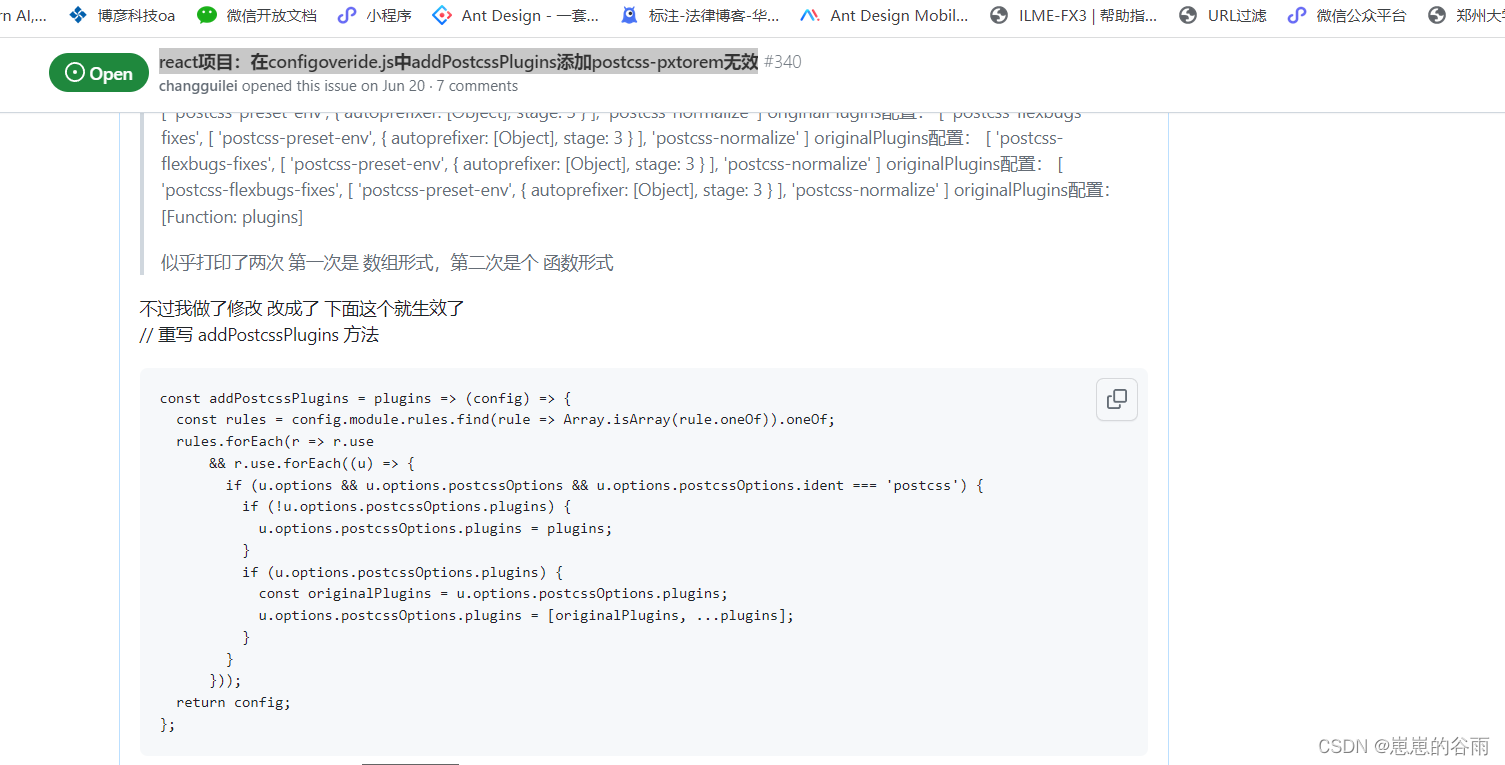
react create-react-app v5配置 px2rem (不暴露 eject方式)
环境信息: create-react-app v5 “react”: “^18.2.0” “postcss-plugin-px2rem”: “^0.8.1” 配置步骤: 不暴露 eject 配置自己的webpack: 1.下载react-app-rewired 和 customize-cra-5 npm install react-app-rewired customize-cra…...

.net中用标志位解决socket粘包问题
以下为wpf中, 用标志位"q" 解决粘包问题 using MyFrameWorkWpf.Entities; using System.Collections.ObjectModel; using System.Net; using System.Net.Sockets; using System.Text; using System.Threading; using System.Threading.Tasks; using System.Windows.…...

【Ubuntu】Systemctl 管理 MinIO 服务器的启动和停止
要使用 systemctl 来管理 MinIO 服务器的启动和停止,您需要创建一个 systemd 服务单元文件,以便 systemd 能够启动和停止 MinIO 服务器。下面是一般的步骤: 创建 systemd 服务单元文件: 打开终端并使用文本编辑器创建一个新的 sys…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
