从零开始的力扣刷题记录-第八十七天
力扣每日四题
- 129. 求根节点到叶节点数字之和-中等
- 130. 被围绕的区域-中等
- 437. 路径总和 III-中等
- 376. 摆动序列-中等
- 总结
129. 求根节点到叶节点数字之和-中等
题目描述:
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
题解:
简单的深度优先搜索就可以解决
代码(Go):
func sumNumbers(root *TreeNode) int {return dfs(root,0)
}func dfs(root *TreeNode,sum int) int {if root == nil {return sum}sum = sum * 10 + root.ValNewSum := 0if root.Left == nil && root.Right == nil{return sum}if root.Left != nil{NewSum += dfs(root.Left,sum)}if root.Right != nil{NewSum += dfs(root.Right,sum)}return NewSum
}
130. 被围绕的区域-中等
题目描述:
给你一个 m x n 的矩阵 board ,由若干字符 ‘X’ 和 ‘O’ ,找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。
题解:
没有被包围的O一定与边界上的O相连,所以可以反过来从边界上的O开始找到所有相连的O并标记,最后遍历矩阵,被标记的O变回O,没有被标记的O改为X
代码(Go):
func solve(board [][]byte) {for i := 0;i < len(board);i++{for j := 0;j < len(board[0]);j++{if (i == 0 || j == 0 || i == len(board) - 1 || j == len(board[0]) - 1) && board[i][j] == 'O'{checkout(board,i,j)board[i][j] = '1'}}}for i := 0;i < len(board);i++{for j := 0;j < len(board[0]);j++{if board[i][j] == '1'{board[i][j] = 'O'}else{board[i][j] = 'X'}}}return
}func checkout(board [][]byte,x int,y int) {if x - 1 >= 0 && board[x - 1][y] == 'O'{board[x - 1][y] = '1'checkout(board,x - 1,y)}if y - 1 >= 0 &&board[x][y - 1] == 'O'{board[x][y - 1] = '1'checkout(board,x,y - 1)}if x + 1 < len(board) && board[x + 1][y] == 'O'{board[x + 1][y] = '1'checkout(board,x + 1,y)}if y + 1 < len(board[0]) && board[x][y + 1] == 'O'{board[x][y + 1] = '1'checkout(board,x,y + 1)}return
}
437. 路径总和 III-中等
题目描述:
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
题解:
代码写麻烦了,官方题解更容易懂。我的思路是用一个flag变量标记此节点是否必选,如果此节点的父节点已经被选中到路径中则该节点必须被选择,然后就是常规的深度优先搜索统计即可
代码(Go):
func pathSum(root *TreeNode, targetSum int) int {return search(root,targetSum,0)
}func search(root *TreeNode,targetSum int,flag int) int {if root == nil{return 0}if root.Val == targetSum && flag == 0{return 1 + search(root.Left,0,1) + search(root.Right,0,1) + search(root.Left,targetSum,0) + search(root.Right,targetSum,0)}else if root.Val == targetSum && flag == 1{return 1 + search(root.Left,0,1) + search(root.Right,0,1)}else if flag == 0{return search(root.Left,targetSum,0) + search(root.Right,targetSum,0) + search(root.Left,targetSum - root.Val,1) + search(root.Right,targetSum - root.Val,1)}else{return search(root.Left,targetSum - root.Val,1) + search(root.Right,targetSum - root.Val,1)}
}
376. 摆动序列-中等
题目描述:
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如, [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ,因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
相反,[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
题解:
子序列问题直接想到动态规划,整体思路和最长递增子序列问题基本一致,但是因为每次判断dp[i]时都需要和前面所有的位置依次对比,所以时间复杂度是O(n²),官方题解使用了两个dp数组分别表示最后一个元素是上升状态的上升数组和最后一个元素是下降状态的下降数组,两个数组的第n个状态都可以通过两个数组的n-1个状态共同得出,这样既使时间复杂度降到了O(n),也使空间复杂度降到了O(1),具体可以看下官方题解
代码(Go):
func wiggleMaxLength(nums []int) int {dp := make([]int,len(nums))sign := make([]int,len(nums))for i := 0;i < len(nums);i++{if i == 0{dp[i] = 1sign[i] = 0}else if i == 1{if nums[i] > nums[0]{sign[i] = 1dp[i] = 2}else if nums[i] < nums[0]{sign[i] = -1dp[i] = 2}else{sign[i] = 0dp[i] = 1}}else{max := 0for j := 0;j < i;j++{if sign[j] == 1 && nums[i] < nums[j]{if dp[j] + 1 > max{max = dp[j] + 1sign[i] = -1}}else if sign[j] == -1 && nums[i] > nums[j]{if dp[j] + 1 > max{max = dp[j] + 1sign[i] = 1}}else if sign[j] == 0{if dp[j] + 1 > max && nums[i] > nums[j]{max = dp[j] + 1sign[i] = 1}else if dp[j] + 1 > max && nums[i] < nums[j]{max = dp[j] + 1sign[i] = -1}}}dp[i] = max}}max := 0for i := 0;i < len(nums);i++{if dp[i] > max{max = dp[i]}}return max
}
总结
终于忙完了一个大阶段,正式回归!但是因为现在还要上课而且两道简单两道中等现在变成了四道中等,所以不一定能保证每天全靠自己做完四道题了,只能说尽量完成,如果时间不够的话就只能把没解出来看了题解的题也搬上来了
相关文章:

从零开始的力扣刷题记录-第八十七天
力扣每日四题 129. 求根节点到叶节点数字之和-中等130. 被围绕的区域-中等437. 路径总和 III-中等376. 摆动序列-中等总结 129. 求根节点到叶节点数字之和-中等 题目描述: 给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 …...

【1】c++设计模式——>UML类图的画法
UML介绍 UML:unified modeling language 统一建模语言 面向对象设计主要就是使用UML类图,类图用于描述系统中所包含的类以及他们之间的相互关系,帮助人们简化对系统的理解,他是系统分析和设计阶段的重要产物,也是系统编码和测试的…...

SAP UI5 指定 / 变更版本
SAP UI5 指定 / 变更版本 Currently, SAP Fiori tools support SAP Fiori elements and SAPUI5 freestyle projects with minimum SAPUI5 versions 1.65 or higher. In case there’s a need to test an existing projects with a lower SAPUI5 version, the following worka…...

SpringMVC中异常处理详解
单个控制器异常处理 // 添加ExceptionHandler,表示该方法是处理异常的方法,属性为处理的异常类ExceptionHandler({java.lang.NullPointerException.class,java.lang.ArithmeticException.class})public String exceptionHandle1(Exception ex, Model mo…...
PPT课件培训视频生成系统实现全自动化
前言 困扰全动自化的重要环节,AI语音合成功能,终于可以实现自动化流程,在此要感谢团队不懈的努力和韧性的精神! 实现原理 请参照我的文章《Craneoffice云PPT课件培训视频生成系统》 基本流程 演示视频 PPT全自动 总结 过去实…...
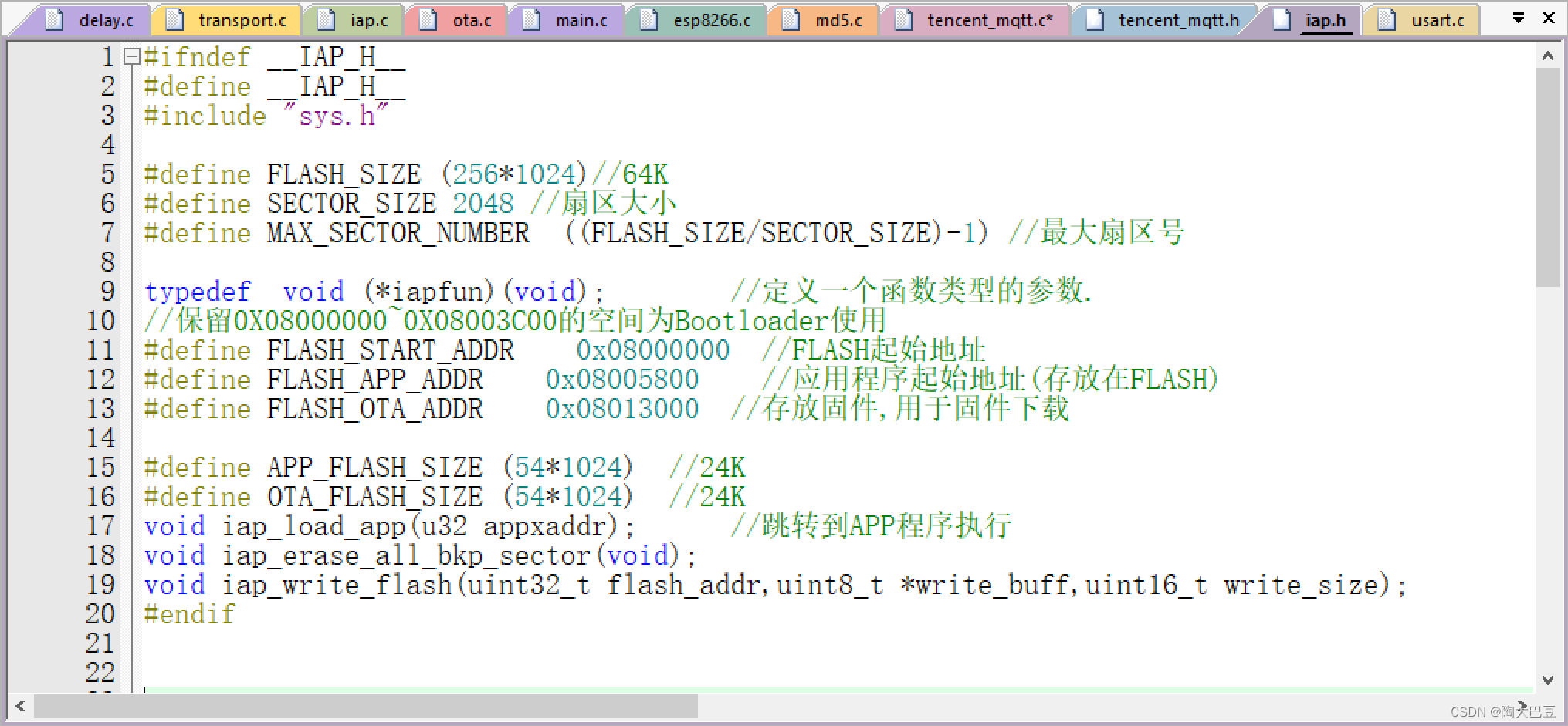
基于腾讯云的OTA远程升级
一、OTA OTA即over the air,是一种远程固件升级技术,它允许在设备已经部署在现场运行时通过网络远程更新其固件或软件。OTA技术有许多优点,比如我们手机系统有个地方做了优化,使用OTA技术我们就不用召回每部手机,直接通过云端就可…...
如何在VS2022中进行调试bug,调试的快捷键,debug与release之间有什么区别
什么是bug 在学习编程的过程中,应该都听说过bug吧,那么bug这个词究竟是怎么来的呢? 其实Bug的本意是“虫子”或者“昆虫”,在1947年9月9日,格蕾丝赫柏,一位为美国海军工作的电脑专家,也是最早…...

初识jmeter及简单使用
目录 1、打开页面: 2、添加线程组: 3、线程组中设置参数: 4、添加请求 5、添加一个http请求后,设置请求内容 6、添加察看结果树 7、执行,查看结果 一般步骤是:在测试计划下面新建一个线程组…...
Spring 在多线程环境下如何确保事务一致性
问题在现 如何解决异步执行 多线程环境下如何确保事务一致性 事务王国回顾 事务实现方式回顾 编程式事务 利用编程式事务解决问题 问题分析完了,那么如何解决问题呢? 小结 问题在现 我先把问题抛出来,大家就明白本文目的在于解决什…...

[Machine Learning] Learning with Noisy Data
文章目录 Probabilistic Perspective of NoiseBias and VarianceRobustness among Surrogate Loss FunctionsNMF Probabilistic Perspective of Noise 假设数据来源于一个确定的函数,叠加了高斯噪声。我们有: y h ( x ) ϵ y h(x) \epsilon yh(x)ϵ…...

C++中有哪些常用的标准库?
C中有许多常用的标准库,这些库提供了丰富的功能和工具,方便开发人员进行各种任务。以下是一些常见的C标准库: iostream:用于输入和输出操作,包括cin、cout和cerr等类和函数。algorithm:提供了许多常用的算…...

软考-信息安全工程师概述
本文为作者学习文章,按作者习惯写成,如有错误或需要追加内容请留言(不喜勿喷) 本文为追加文章,后期慢慢追加 2023年10月 信息考试大纲 通过本考试的合格人员能够掌握网络信息安全的基础知识和技术原理,…...

2023-2024年华为ICT网络赛道模拟题库
2023-2024年网络赛道模拟题库上线啦,全面覆盖网络,安全,vlan考点,都是带有解析 参赛对象及要求: 参赛对象:现有华为ICT学院及未来有意愿成为华为ICT学院的本科及高职院校在校学生。 参赛要求:…...

英特尔参与 CentOS Stream 项目
导读红帽官方发布公告欢迎英特尔参与进 CentOS Stream 项目,并表示 “这一举措不仅进一步深化了我们长期的合作关系,也构建在英特尔已经在 Fedora 项目中积极贡献的基础之上。” 目前,CentOS Stream 共包括以下特别兴趣小组(SIG&a…...

Centos 服务器 MySQL 8.0 快速开启远程访问
环境: MySQL 8.0(低版本会有些不同), Rocky Linux 9.0(CentOS) 直接上干货,相信大家看到这个文章的时候都已经安装完了。 1. 先从服务器上使用 root 进行登录(刚安装完默认只能本地…...
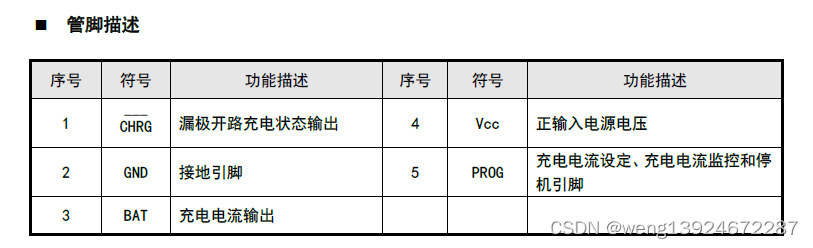
充电保护芯片TP4054国产替代完全兼容DP4054DP4054H 锂电充电芯片
■产品概述 DP4054H是-款完整的采用恒定电流/恒定电压单节锂离子电池充电管理芯片。其SOT小封装和较少的外部元件数目使其成为便携式应用的理想器件,DP4054H可 以适合USB电源和适配器电源工作。 由于采用了内部PMOSFET架构,加上防倒充电路,所以不需要外…...

Java Spring Boot中的爬虫防护机制
随着互联网的发展,爬虫技术也日益成熟和普及。然而,对于某些网站来说,爬虫可能会成为一个问题,导致资源浪费和安全隐患。本文将介绍如何使用Java Spring Boot框架来防止爬虫的入侵,并提供一些常用的防护机制。 引言&a…...

状态模式 行为型模式之六
1.定义 允许一个对象在其对象内部状态改变时改变它的行为。 2.组成结构 Context:定义客户感兴趣的接口;维护一个ConcreteState子类的实例,这个实例定义当前的状态。State:定义一个接口来封装Context的与特定状态相关的行为。Co…...
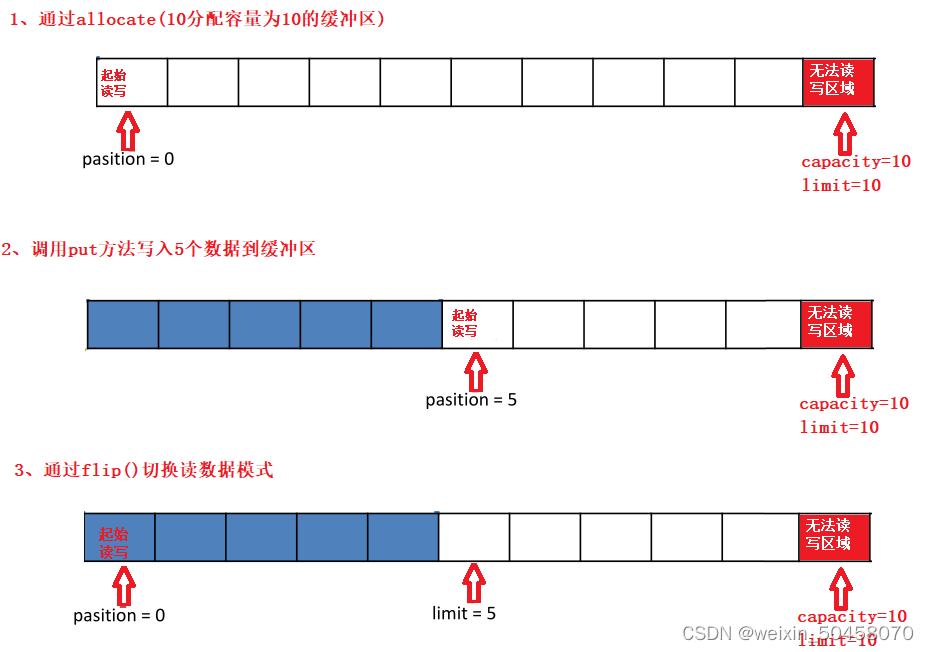
JAVA NIO深入剖析
4.1 Java NIO 基本介绍 Java NIO(New IO)也有人称之为 java non-blocking IO是从Java 1.4版本开始引入的一个新的IO API,可以替代标准的Java IO API。NIO与原来的IO有同样的作用和目的,但是使用的方式完全不同,NIO支持面向缓冲区的、基于通道的IO操作。NIO将以更加高效的方…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...
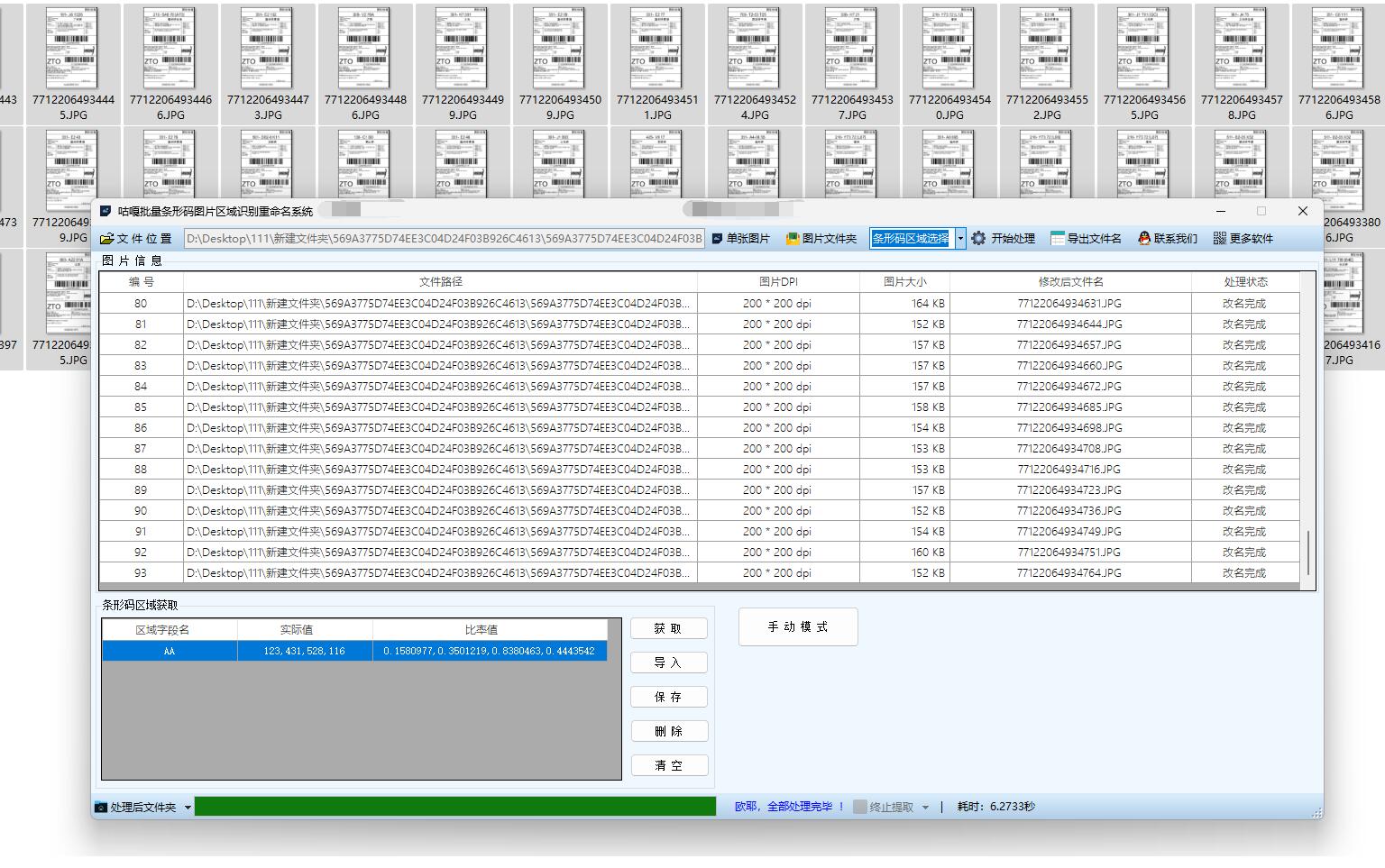
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解
在我的上一篇博客:基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目,该项目展示了一个强大的框架,旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人,更是一个集…...