hive数据表定义
分隔符
CREATE TABLE emp(
userid bigint,
emp_name array<string>,
emp_date map<string,date>,
other_info struct<deptname:string, gender:string>)
ROW FORMAT DELIMITED
FIELDS TERMINATED BY '\t'
COLLECTION ITEMS TERMINATED BY ','
MAP KEYS TERMINATED BY ':';FIELDS TERMINATED BY '\t' --字段之间的分隔符为制表符('\t')
COLLECTION ITEMS TERMINATED BY ',' --集合项之间的分隔符为逗号(',')
MAP KEYS TERMINATED BY ':' --MAP中每个键值对由冒号分隔
如:birth date:1953-11-07,from date:1990-01-22
分区表
create table dept_partition(
deptno int, dname string, loc string)
partitioned by (day string)
row format delimited fields terminated by '\t'; 查询分区表中数据
select * from dept_partition where day='20200401'; 增加分区
alter table dept_partition add partition(day='20200404');alter table dept_partition add partition(day='20200405') partition(day='20200406'); 删除分区
alter table dept_partition drop partition (day='20200406'); alter table dept_partition drop partition (day='20200404'), partition(day='20200405'); 二级分区
create table dept_partition2(
deptno int, dname string, loc string )
partitioned by (day string, hour string)
row format delimited fields terminated by '\t'; 相关文章:

hive数据表定义
分隔符 CREATE TABLE emp( userid bigint, emp_name array<string>, emp_date map<string,date>, other_info struct<deptname:string, gender:string>) ROW FORMAT DELIMITED FIELDS TERMINATED BY \t COLLECTION ITEMS TERMINATED BY , MAP KEYS TERMINAT…...

OpenMesh 网格简化之顶点聚类
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 顶点聚类方法将落在给定大小体素中的所有顶点集中到单个顶点之上,其过程有点类似于点云体素下采样,之后再基于聚类之后的顶点重新连接面片,以达到网格简化的目的。 二、实现代码 #define _USE_MATH_DEFINES #in…...

C++ 类和对象篇(八) const成员函数和取地址运算符重载
目录 一、const成员函数 1. const成员函数是什么? 2. 为什么有const成员函数? 3. 什么时候需要使用const修饰成员函数? 二、取地址运算符重载 1. 为什么需要重载取地址运算符? 2. 默认取地址运算符重载函数 3. 默认const取地址运…...

k8s 集群安装(vagrant + virtualbox + CentOS8)
主机环境:windows 11 k8s版本:v1.25 dashboard版本:v2.7.0 calico版本: v3.26.1 CentOS8版本:4.18.0-348.7.1.el8_5.x86_64 用到的脚本: https://gitcode.net/sundongsdu/k8s_cluster 1. Vagrant创建…...
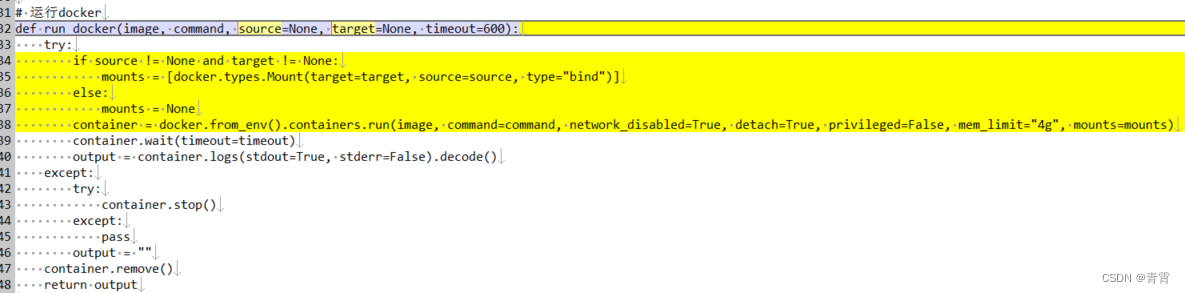
8、Docker数据卷与数据卷容器
一、数据卷(Data Volumes) 为了很好的实现数据保存和数据共享,Docker提出了Volume这个概念,简单的说就是绕过默认的联合文件系统,而以正常的文件或者目录的形式存在于宿主机上。又被称作数据卷。 数据卷 是一个可供一个或多个容器使用的特殊目…...
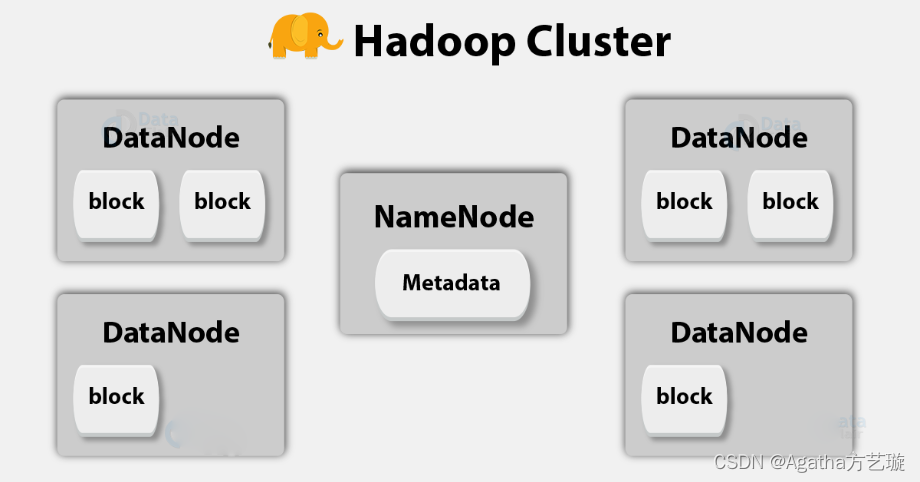
大数据与Hadoop入门理论
一、大数据的3种数据类型 1、结构化数据 可定义,有类型、格式、结构的强制约束 如:RDBMS(关系型数据库管理系统) 2、非结构化数据 没有规律没有数据约束可言,很复杂难以解析 如:文本文件,视…...

持续集成部署-k8s-深入了解 Pod:探针
持续集成部署-k8s-深入了解 Pod:探针 1. 探针分类2. 探针探测方式3. 探针参数配置4. 启动探针的应用5. Liveness 探针的应用6. Readiness 探针的应用1. 探针分类 Kubernetes 中的探针是指容器内的进程用于告知 Kubernetes 组件其自身状态的机制; Readiness Probe:就绪探针用…...
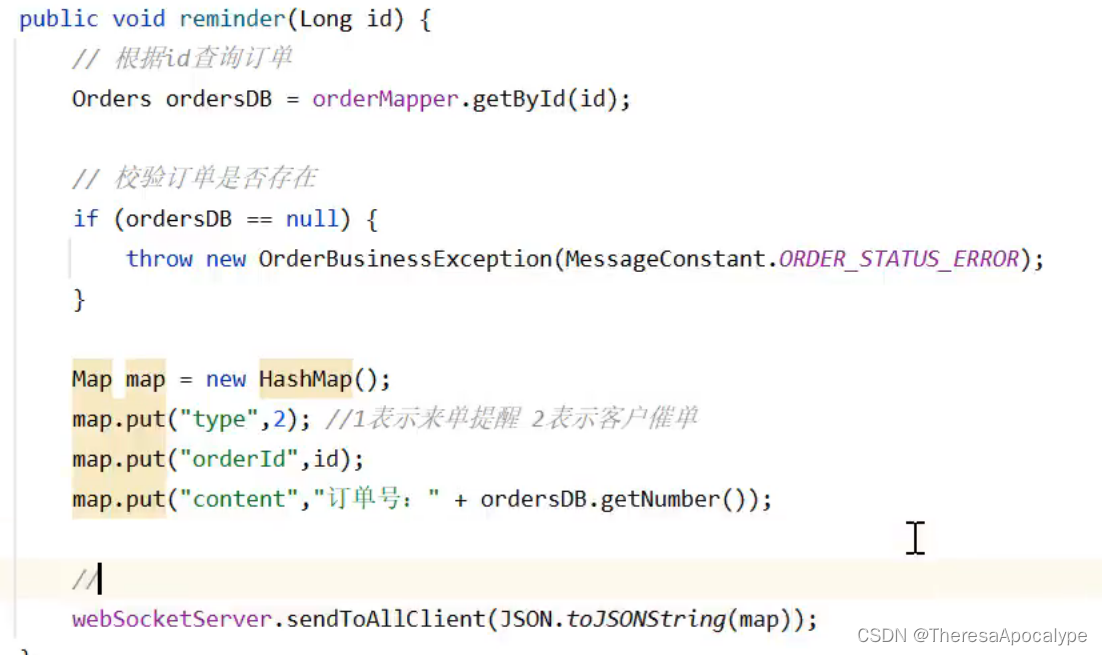
来单提醒/客户催单 ----苍穹外卖day9
来单提醒 需求分析 代码开发 注意:前端请求的并不是8080端口;而是先请求Nginx,Nginx进行反向代理以后转发到8080端口 这段代码首先创建了一个orders类用于更新订单状态 并且在更新状态后使用websocket发送给后端提醒 将信息放在map后,使用json的string化方式传给一个接收对象,…...
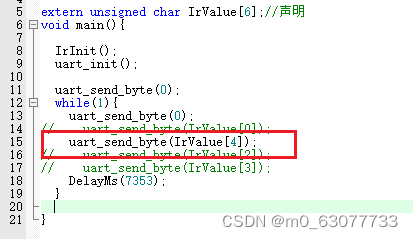
【单片机】18-红外线遥控
一、红外遥控背景知识 1.人机界面 (1)当面操作:按键,旋转/触摸按键,触摸屏 (2)遥控操作:红外遥控,433M/2.4G无线通信【穿墙能力强】,蓝牙-WIFI-Zigbee-LoRa等…...

【Node.js】module 模块化
认识 node.js Node.js 是一个独立的 JavaScript 运行环境,能独立执行 JS 代码,可以用来编写服务器后端的应用程序。基于Chrome V8 引擎封装,但是没有 DOM 和 BOM。Node.js 没有图形化界面。node -v 检查是否安装成功。node index.js 执行该文…...

Vue中如何进行分布式日志收集与日志分析(如ELK Stack)
在Vue中实现分布式日志收集与日志分析(使用ELK Stack) 日志收集和分析在现代应用程序中是至关重要的,它们可以帮助开发人员监视和诊断应用程序的行为,从而提高应用程序的稳定性和性能。ELK Stack(Elasticsearch、Logs…...
)
java学习--day23(线程池)
1.线程池Pool 线程池一个容纳了多个线程的容器,其中的线程可以反复的使用。省去了频繁创建线程的对象的操作,无需反复创建线程而消耗更多的资源 在 Java 语言中,并发编程都是通过创建线程池来实现的,而线程池的创建方式也有很多种…...

Unity Golang教程-Shader编写一个流动的云效果
创建目录 一个友好的项目,项目目录结构是很重要的。我们先导入一个登录界面模型资源。 我们先创建Art表示是美术类的资源,资源是模型创建Model文件夹,由于是在登录界面所以创建Login文件夹,下面依次是模型对应的资源,…...

Python数据攻略-Pandas与地理空间数据分析
地理空间数据分析已经成为数据分析不可或缺的一部分。无论是在城市规划、交通分析,还是在环境科学中,地理空间数据都发挥着关键作用。 本文将为初学者和新手提供一个详细的指南,通过使用Python的Pandas库和Geopandas库,来进行地理空间数据分析。 文章目录 用Pandas处理地理…...

sourceTree无法启动
前几天win10系统自动更新后,sourceTree就无法打开了,双击只是图标闪一下,电脑重启后还是无法打开。找到了网上几种方法进行尝试: 方法一:修改配置信息 在自己的电脑路径下: C:\Users\你的用户名\AppData…...

【ARM Coresight 系列文章19 -- Performance Monitoring Unit(性能监测单元)
文章目录 1.1 PMU 介绍1.2 PMU 寄存器1.2.1 PMU 管理寄存器1.2.2 PMU 外设识别寄存器1.2.3 PMU 组件识别寄存器1.3 性能监控事件1.3.1 Cortex-A9 特定事件1.1 PMU 介绍 许多体系结构都包含 PMU(Performance Monitoring Unit)硬件,用于跟踪、计数系统内部的一些底层硬件事件…...
前端学习| 第二章
CSS学习|第一章 前言一、概述1. 语法规定2. 代码风格 二、选择器1. 基础选择器标签选择器类选择器id选择器通配符选择器 2. 复合选择器后代选择器子元素选择器并集选择器伪类选择器链接伪类选择器focus 伪类选择器 三、引入方式四、显示模式1. 块元素2. 行内元素3. 行内块元素4…...
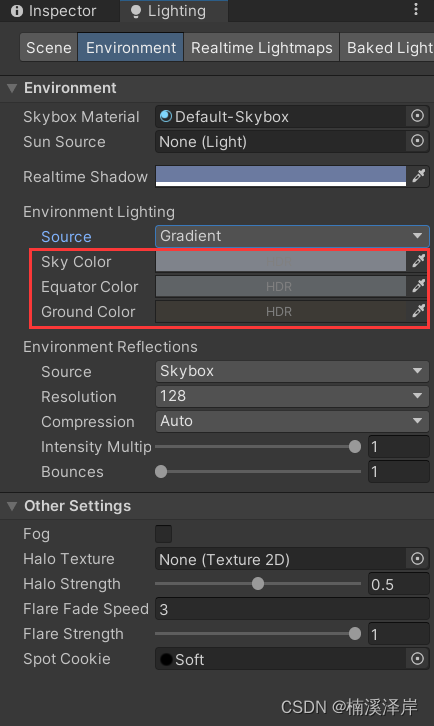
Unity中Shader光强与环境色
文章目录 前言一、实现下图中的小球接受环境光照实现思路:1、在Pass中使用前向渲染模式2、使用系统变量 _LightColor0 获取场景中的主平行灯 二、返回环境中主环境光的rgb固定a(亮度),小球亮度还随之改变的原因三、获取Unity中的环境光的颜色1、Color模式…...

Android9 查看连接多个蓝牙耳机查看使用中的蓝牙耳机
#Android9 查看连接多个蓝牙耳机查看使用中的蓝牙耳机 文章目录 一、主要api:二、BluetoothA2dp 对象的获取三、获取 BluetoothDevice 对象,四、其他: Android 9.0之后,支持一台手机可以同时连接多个蓝牙设备。 但是判断那个蓝牙…...
)
【EF Core】如何忽略影响导航属性(级联)
文章目录 EF更新和插入时如何忽略更新导航属性级联删除删除主体/父实体断开关系配置级联行为 来源 EF更新和插入时如何忽略更新导航属性 使用Ignore方法: modelBuilder.Entity<Blog>().Ignore(b > b.Posts);使用HasNoKey方法: modelBuilder.…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
