COCI 2021-2022 #1 - Set 题解
思路
我们将原题中的数的每一位减一,此时问题等价。
下面的异或都是在三进制下的异或。(相当于不进位的加法)
我们考虑原题中的条件,对于每一位,如果相同,则异或值为 0 0 0,如果为 1 1 1, 2 2 2, 3 3 3 的排列,则异或值也为 0 0 0。
于是我们设 C k C_k Ck 表示有没有 k k k 这个数, a n s = ∑ i ⊕ j ⊕ k = 0 c i ⋅ c j ⋅ c k ans=\sum_{i\oplus j\oplus k = 0} c_i\cdot c_j\cdot c_k ans=∑i⊕j⊕k=0ci⋅cj⋅ck,则答案为 a n s − n 6 \frac{ans - n}{6} 6ans−n。
其中 a n s ans ans 可以用 FWT 求,具体实现可以看我的博客。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n, k, len = 1;
LL ans;
complex <double> a[1000005];
const complex <double> w = {-0.5, 0.5 * sqrt(3)}, w2 = {-0.5, -0.5 * sqrt(3)};
int in() {char ch = getchar();int s = 0;while (ch < '0' || ch > '9')ch = getchar();while (ch <= '9' && ch >= '0')s = s * 3 + ch - '1', ch = getchar();return s;
}
void FWT(complex <double> *f, int flag) {for (int mid = 1; mid < len; mid = mid * 3) {for (int i = 0; i < len; i = i + mid * 3) {for (int j = i; j < i + mid; j++) {complex <double> t0 = f[j], t1 = f[j + mid], t2 = f[j + mid * 2];if (flag == 1) {f[j] = t0 + t1 + t2;f[j + mid] = t0 + t1 * w + t2 * w2;f[j + mid * 2] = t0 + t1 * w2 + t2 * w;}else {f[j] = t0 + t1 + t2;f[j + mid] = t0 + t1 * w2 + t2 * w;f[j + mid * 2] = t0 + t1 * w + t2 * w2;double t;t = f[j].real(), f[j].real(t / 3);t = f[j + mid].real(), f[j + mid].real(t / 3);t = f[j + mid * 2].real(), f[j + mid * 2].real(t / 3);t = f[j].imag(), f[j].imag(t / 3);t = f[j + mid].imag(), f[j + mid].imag(t / 3);t = f[j + mid * 2].imag(), f[j + mid * 2].imag(t / 3);}}}}
}
int main() {scanf("%d%d", &n, &k);for (int t = 0; t < k; t++)len = len * 3;for (int i = 0; i < n; i++)a[in()].real(1);FWT(a, 1);for (int i = 0; i < len; i++)a[i] = a[i] * a[i] * a[i];FWT(a, -1);ans = a[0].real() + 0.5;printf("%lld\n", (ans - n) / 6);return 0;
}
相关文章:

COCI 2021-2022 #1 - Set 题解
思路 我们将原题中的数的每一位减一,此时问题等价。 下面的异或都是在三进制下的异或。(相当于不进位的加法) 我们考虑原题中的条件,对于每一位,如果相同,则异或值为 0 0 0,如果为 1 1 1&a…...

分享40个极具商业价值的chatGPT提问prompt
原文:分享40个极具商业价值的chatGPT提问prompt | 秋天的童话博客 1、分析并改善定价策略 提示: "分析我当前的[插入产品或服务]定价策略。提出改进建议,并帮助我制定新的定价策略,以最大化利润和客户满意度。" Analyze and Imp…...

一文搞懂到底什么是元宇宙
一、背景 2021年,“元宇宙”是科技界的开端。 2021”元宇宙”这个词在Facebook更名后被点燃了,无疑是21世纪科技界最爆的起点。各式各样的定义、解读都出现了,有人说它是炒作,甚至是骗局,但也有人说它就是互联网的未…...

【重拾C语言】六、批量数据组织(四)线性表—栈和队列
目录 前言 六、批量数据组织——数组 6.1~3 数组基础知识 6.4 线性表——分类与检索 6.5~7 数组初值;字符串、字符数组、字符串数组;类型定义 typedef 6.8 线性表—栈和队列 6.8.1 栈(Stack) 全局变量 isEmpty() isFull…...

力扣刷题-哈希表-一个字符串是否能够由另一个字符串中的字符组成
383 赎金信 给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。 如果可以,返回 true ;否则返回 false 。 magazine 中的每个字符只能在 ransomNote 中使用一次。ransomNote 和 magazin…...

Android使用AOP切面编程
在Android应用程序中,AOP可以被用于许多不同的场景,例如日志记录、权限控制、性能分析等。下面是一个简单的例子,说明如何在Android应用程序中使用AOP切面编程。 首先,我们需要在应用程序中引入AspectJ库。我们可以使用Gradle来完…...

Flutter学习笔记
此篇文章用来记录学习Flutter 和 Dart 相关知识 零.Dart基本数据类型 Dart 是一种静态类型的编程语言,它提供了一系列基本数据类型,用于存储和操作不同种类的数据。以下是 Dart 中的一些基本数据类型以及它们的详细介绍: 1. 整数类型&#…...

软件生命周期中的概念设计和详细设计的主要任务是什么
基础概念 在软件生命周期中,概念设计和详细设计是软件设计阶段中的两个重要环节。 概念设计阶段的主要任务是从业务需求出发,将系统的基本概念、主要功能和关键特性进行抽象和定义。概念设计旨在确定系统的整体架构和关键模块,包括以下主要…...
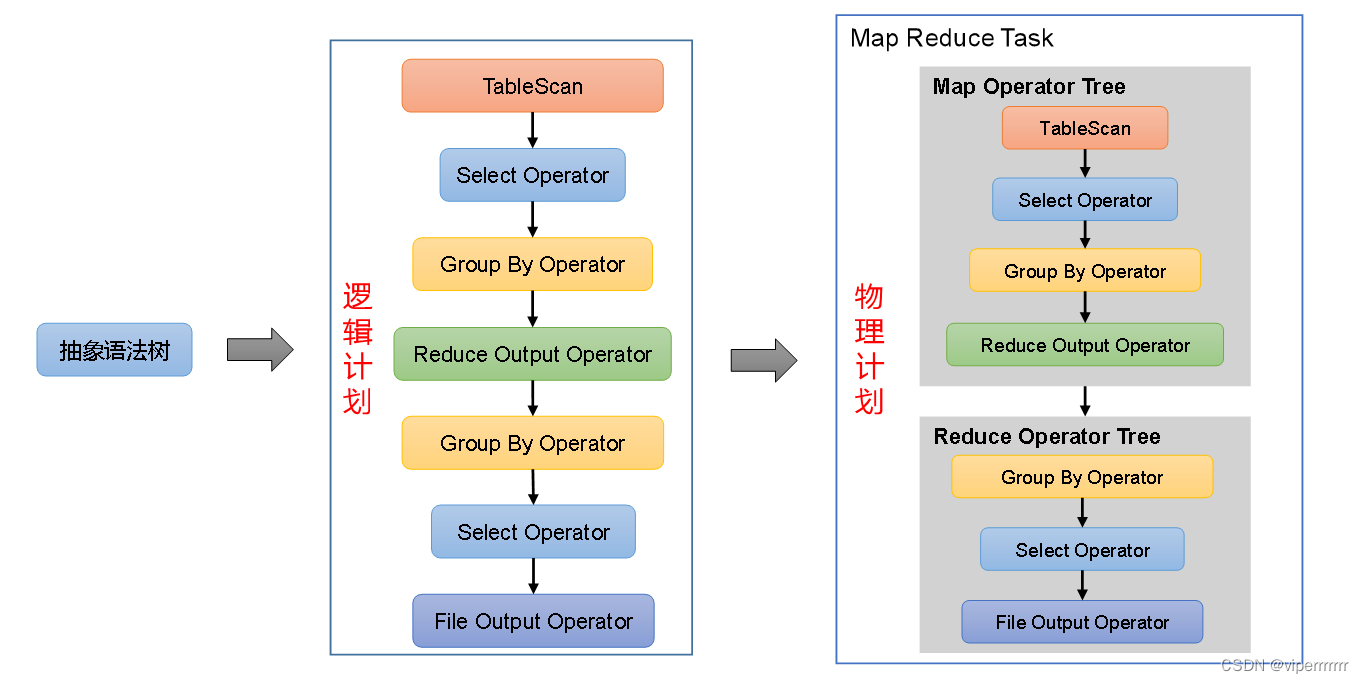
大数据学习(2)Hadoop-分布式资源计算hive(1)
&&大数据学习&& 🔥系列专栏: 👑哲学语录: 承认自己的无知,乃是开启智慧的大门 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一下博>主哦&#x…...

深入探究HTML表单与JavaScript的关系
深入探究HTML表单与JavaScript的关系 引言 HTML表单是网页中数据收集的重要工具,而JavaScript则充当着这些数据的处理者和控制者的角色。二者之间的关系非常紧密,共同构成了现代Web应用中用户交互的基础。在这篇博客中,我们将详细地解析HTM…...
关于Jupyter notebook 创建python3 时进去不能重命名问题及不能编程问题
首先写这篇博客时,已经被这个问题折磨了三天,看了很多博客,其实解决这个问题的关键就是要么没有下pyzmq或者等级太高,要么等级太低,首先我会按照我思路来。 问题如图: 1.自动换行 2.不能重命名 我的解决办…...

一些可以用代码绘制流程图的工具
代码绘制流程图的工具有很多,以下是一些常用的工具: Mermaid:Mermaid 是一个基于 Markdown 的图表语言,可以生成各种类型的图表,包括流程图、时序图、甘特图等。Mermaid 可以使用 JavaScript 或 TypeScript 进行编写,可以通过 Node.js 运行。Graphviz:Graphviz 是一个开…...
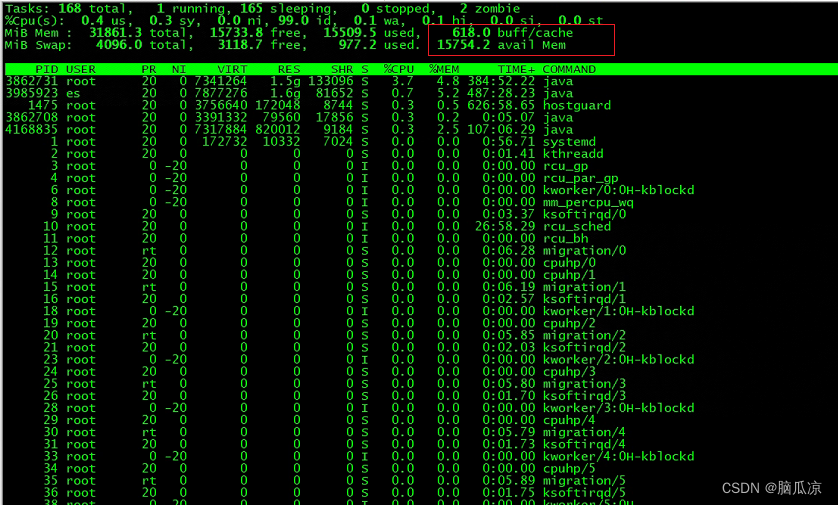
Centos中清除因程序异常终止,导致的残留的Cache/buff_drop_caches命令---linux工作笔记063
我这里因为nifi程序背压设置的不合理,导致,内存和CPU消耗过高,系统崩溃,但是重启NIFI以后,发现 对应的执行top命令,看到,系统的buff/cache 依然没有减少,说明内存被浪费了,残留在这里没有被回收. 用这个办法执行这个命令; linux会自动触发清理,但是只有在内存不够用的时候才会…...
)
Element-UI的使用——表格el-table组件去除边框、滚动条设置、隔行变色、去除鼠标悬停变色效果(基于less)
// Element-ui table表格去掉所有边框,如下: // 备注:若去掉所有边框,可自行将头部边框注释掉即可 // 该样式写在style scoped外面在el-table 中添加class"customer-table"类名 //去掉每行的下边框/deep/ .el-table td.el-table__c…...

python的一些知识点
之前自学过python,学了一些基本语法,但忘得厉害。最近,在努力地写代码,在学代码,写代码中学习python,为此记录一些关于python的知识点。...
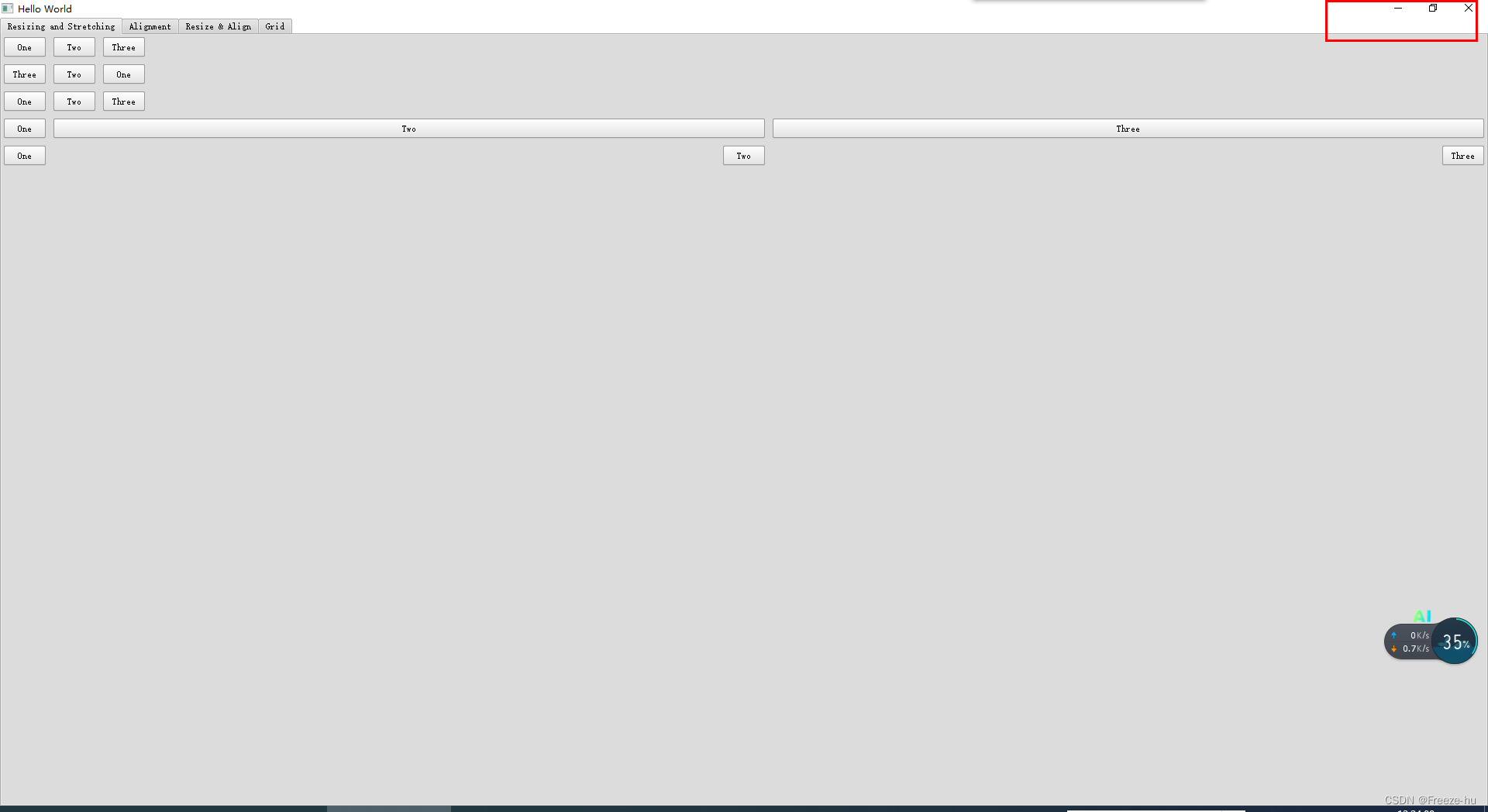
QML 带框最大化显示方法
1.QML窗口最大化很多会给出如下方法: visibility: "FullScreen" 此方法不好的方面是没有最大化,最小化,关闭按钮 2.通过showMaximized() 方法可以满足我们需求:在onCompleted 方法中执行 实现的效果如下:...

conda命令大全
conda list 查看环境中已经安装了的软件包 conda list --name your_env_name(虚拟环境名) 查看某个环境下的包 conda config --show 查看现有源 conda env list 或者 conda info -e 查看当前存在那些虚拟环境 conda update conda 更新至最新的conda版本 conda update [pac…...

国庆要闻回顾 | OpenAI 拟研发 AI 手机;9月以太坊上NFT销售量创2021年2月以来最低记录...
国庆期间区块链行业要闻回顾:产业方面,全国区块链行业产教融合共同体在雄安新区成立,巴西推出基于区块链的数字身份证,瑞银集团在以太坊上推出代币化货币市场基金试点,NASA拟在月球设立区块链数据中心以保存国家机密资…...
国家开放大学 模拟试题 训练
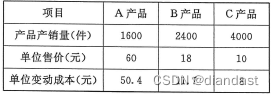
试卷代号:2136 管理会计 参考 试题 一、单项选择题(每小题1分,共20分) 1.管理会计依靠各种功能来助力企业战略,下列哪项是管理会计的核心功能( )。 A.评价功能 B.预测功能 C.决策功能…...

【GIT版本控制】--常见问题与解决方案
一、修复损坏的仓库 修复损坏的Git仓库可能是面临的一种问题,这通常是由于文件损坏、存储介质问题或不正确的操作等原因引起的。以下是一些修复损坏的Git仓库的常见问题和解决方案: 常见问题: 无法执行Git命令:当尝试运行Git命令…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
