LeetCode动态规划经典题目(九):子序列、子数组问题
目录
31. LeetCode674. 最长连续递增序列
32. LeetCode18. 最长重复子数组
33. LeetCode1143. 最长公共子序列
34. LeetCode1035. 不相交的线
35. LeetCode53. 最大子数组和
36. LeetCode392.判断子序列
37. LeetCode115. 不同的子序列
38. LeetCode583. 两个字符串的删除操作
39. LeetCode72. 编辑距离
思路:
1.dp含义:
dp[i]:集合nums从下标0到下标i并且以nums[i]结尾的最长递增子序列长度
(1)为什么能够以nums[i]结尾?因为每个递增子序列必定是以集合nums中的其中一个元素结尾。
(2)为什么一定要以nums[i]结尾?因为在递推时,我们需要与前一个递增子序列作比较,而只有知道尾元素大小才能有效地比较。
2.转移方程:
if(nums[j]<nums[i])dp[i]=max(dp[i],dp[j]+1);//j:0~(i-1)
3.初始化dp:
dp[0]=1;方法一:动态规划
class Solution {
public:int lengthOfLIS(vector<int>& nums) {if(nums.size()<=1)return nums.size();//dp[i]:集合nums从下标0到下标i并且以nums[i]结尾的最长递增子序列长度vector<int>dp(nums.size(),1);//基础长度是1int res=0;//完善dpfor(int i=1;i<nums.size();i++){for(int j=0;j<i;j++){if(nums[j]<nums[i])dp[i]=max(dp[i],dp[j]+1);//保留以nums[i]结尾最大长度}res=max(dp[i],res);//保留整体集合最长递增子序列长度}return res;}
};
时间复杂度:O(n^2)
空间复杂度:O(n)方法二:贪心+动态规划
ends[i]:所有长度为i+1的递增子序列的尾元素最小值,且ends[i]必定小于ends[i+1]
为什么ends[i]<ends[i+1]?设以ends[i]、ends[i+1]结尾的递增子序列分别为subSequence1(长度为i+1),subSequence2(长度为i+2),
假设ends[i]>ends[i+1],即subSequence1[i]>subSequence2[i+1],由于递增,
所以subSequence1[i]>subSequence2[i+1]>subSequence2[i] => subSequence1[i]>subSequence2[i]
则 ends[i]=subSequence2[i],有矛盾,所以假设不成立。class Solution {
public:int lengthOfLIS(vector<int>& nums) {if(nums.size()<=1)return nums.size();//ends[i]:所有长度为i+1的递增子序列的尾元素最小值,且ends[i]必定小于ends[i+1]vector<int>ends(nums.size());ends[0]=nums[0];int right=0;for(int i=1;i<nums.size();i++){//长度最长的递增子序列尾元素小于nums[i],有效区域右移,并记录最小尾元素if(ends[right]<nums[i]){ends[++right]=nums[i];}else{int l=0;while(l<right&&ends[l]<nums[i]){//找到ends最左边比nums[i]大的尾元素l++;}//退出循环有两种情况,只有第二种情况才能赋值if(ends[l]>nums[i])ends[l]=nums[i];}}//ends[right]是"长度为right+1"的递增子序列的最小尾元素return right+1;}
};
时间复杂度:O(n*logn)
空间复杂度:O(n)31. LeetCode674. 最长连续递增序列
1.dp[i]:以nums[i]结尾的连续递增序列长度
2.if(nums[i]>nums[i-1])dp[i]=dp[i-1]+1:因为是连续的,所以只需要考虑nums[i]是否比nums[i-1]大就行了(贪心)
3.初始化dp:全都初始化成1,因为至少包含nums[i]动态规划:
class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {if(nums.size()<=1)return nums.size();//dp[i]:以nums[i]结尾的连续递增序列长度vector<int>dp(nums.size(),1);int res=INT_MIN;//完善dpfor(int i=1;i<nums.size();i++){if(nums[i]>nums[i-1])dp[i]=dp[i-1]+1;res=max(res,dp[i]);//记录最长连续递增序列长度}return res;}
};贪心:
class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {if(nums.size()<=1)return nums.size();int count=1;//记录过程中个递增序列长度int res=INT_MIN;//记录最长递增序列长度for(int i=1;i<nums.size();i++){if(nums[i]>nums[i-1])count++;else count=1;//重新取递增序列头元素res=max(res,count);}return res;}
};与前一题的区别是:
本题dp[i]状态之和dp[i-1]有关,因为是连续的。
而前一题因为是不连续的,所以dp[i]状态和dp[0]/dp[1]/.../dp[i-1]都有关系32. LeetCode18. 最长重复子数组
1.dp[i][j]:以nums1[i]结尾的nums1和以nums2[j]结尾的nums2的重复子数组长度
2.if(nums1[i]==nums[j])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=0;
3.初始化dp普通动态规划二维表:
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {//长度是1,看唯一元素是否相同if(nums1.size()==1&&nums2.size()==1)return nums1[0]==nums2[0]?1:0;//dp[i][j]:以nums1[i]结尾的nums1和以nums2[j]结尾的nums2的重复子数组长度vector<vector<int>>dp(nums1.size(),vector<int>(nums2.size()));//记录最长重复子数组长度int res=0;//初始化dpfor(int i=0;i<nums1.size();i++){if(nums1[i]==nums2[0])dp[i][0]=1;res=max(res,dp[i][0]);}for(int j=0;j<nums2.size();j++){if(nums2[j]==nums1[0])dp[0][j]=1;res=max(res,dp[0][j]);}//完善dpfor(int i=1;i<nums1.size();i++){for(int j=1;j<nums2.size();j++){if(nums1[i]==nums2[j]){dp[i][j]=dp[i-1][j-1]+1;}else{//如果nums1[i]!=nums2[j],那必不可能重复,因为子数组一定要包含nums1[i]和nums2[j]dp[i][j]=0;}res=max(res,dp[i][j]);}}return res;}
};观察上方代码,发现不仅要额外判断数组长度为1时的情况,还要在初始化dp时更新res,代码略显臃肿。
再看转移方程,我们可以多一行一列,基础值为0,但也因此有额外空间开销
1.dp[i][j]:以nums1[i-1]结尾的nums1和以nums2[j-1]结尾的nums2的重复子数组长度
2.if(nums1[i]==nums[j])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=0;
3.初始化dp
改良动态规划二维表(代码行数更少):
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {//dp[i][j]:以nums1[i-1]结尾的nums1和以nums2[j-1]结尾的nums2的重复子数组长度vector<vector<int>>dp(nums1.size()+1,vector<int>(nums2.size()+1));//记录最长重复子数组长度int res=0;//完善dpfor(int i=1;i<nums1.size()+1;i++){for(int j=1;j<nums2.size()+1;j++){if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=0;res=max(res,dp[i][j]);}}return res;}
};滚动数组:
观察转移方程,dp是一行一行更新,并且是从左到右
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<int>dp(nums2.size()+1);int res=0;for(int i=1;i<nums1.size()+1;i++){for(int j=nums2.size();j>=1;j--){//滚动数组应当优先更新那些不用来递推其他dp值的if(nums1[i-1]==nums2[j-1])dp[j]=dp[j-1]+1;else dp[j]=0;res=max(res,dp[j]);}}return res;}
};总结:
实现出动态规划二维表后,观察转移方程,看是否能够利用滚动数组实现,一般来说一行一行遍历的都可以转成一维数组。33. LeetCode1143. 最长公共子序列
1.dp[i][j]:text1[0,i-1]和text2[0,j-1]的最长公共子序列长度
2.if(text[i]==text[j])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);class Solution {
public:int longestCommonSubsequence(string text1, string text2) {//dp[i][j]:text1[0,i-1]和text2[0,j-1]的最长公共子序列长度vector<vector<int>>dp(text1.length()+1,vector<int>(text2.length()+1));//完善dpfor(int i=1;i<text1.length()+1;i++){for(int j=1;j<text2.length()+1;j++){if(text1[i-1]==text2[j-1]){dp[i][j]=dp[i-1][j-1]+1;}else{//text1[i-1]!=text2[j-1]//1.text1[i-2]和text[j-1]比较//2.text1[i-1]和text[j-2]比较//上述两种情况已经涵盖了所有可能性:text1[i-2]子序列涵盖了text1[i-3]所有子序列//text1[i-1]和text2[j-1]是新出现的字符,所以必须带着dp[i][j]=max(dp[i-1][j],dp[i][j-1]);//记忆化搜索}}}return dp[text1.length()][text2.length()];}
};34. LeetCode1035. 不相交的线
思路:
线只要在连接nums1和nums2的元素时按照相对同样的顺序就不会相交,所以本质上是求nums1和nums2最长公共子序列长度。1.dp[i][j]:nums1[0,i-1]和nums2[0,j-1]的公共子序列长度
2.if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {//dp[i][j]:nums1[0,i-1]和nums2[0,j-1]的公共子序列长度vector<vector<int>>dp(nums1.size()+1,vector<int>(nums2.size()+1));//完善dpfor(int i=1;i<nums1.size()+1;i++){for(int j=1;j<nums2.size()+1;j++){if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i][j-1],dp[i-1][j]);}}return dp[nums1.size()][nums2.size()];}
};35. LeetCode53. 最大子数组和
1.dp[i]:以nums[i-1]结尾的最大子数组和
2.if(dp[i-1]>0)dp[i]=dp[i-1]+nums[i];else dp[i]=nums[i-1];class Solution {
public:int maxSubArray(vector<int>& nums) {//dp[i]:以nums[i]结尾的最大子数组和vector<int>dp(nums.size()+1);int res=INT_MIN;//完善dpfor(int i=1;i<nums.size()+1;i++){//只有前面子数组和为正,才对自己有帮助,才能够获取最大子数组和if(dp[i-1]>0)dp[i]=dp[i-1]+nums[i-1];else dp[i]=nums[i-1];res=max(res,dp[i]);}return res;}
};dp[i]只与dp[i-1]有关,与dp[i-1]前的元素都无关,所以我们只需一个值即可
class Solution {
public:int maxSubArray(vector<int>& nums) {int cur=0;int res=INT_MIN;for(int i=0;i<nums.size();i++){if(cur>=0){cur=cur+nums[i];}else{//cur<0,只会减少后续子数组和cur=nums[i];}res=max(res,cur);}return res;}
};36. LeetCode392.判断子序列
1.dp含义:
dp[i][j]:以s[i-1]结尾的字符串s,和以t[j-1]结尾的字符串t,相同子序列长度
注意:是判断s是否为t的子序列,所以t.length()>=s.length();s一定要包含s[i-1],t不一定要包含t[j-1]2.转移方程:
只需要考虑删除字符串t的元素即可
if(s[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1]+1;//t中新出现的字符能够和s[i-1]匹配
else dp[i][j]=dp[i][j-1];//无法匹配,t删除元素,继续匹配,然前一个字符去处理3.初始化dp:
//初始化二维数组dp时就已经完成了
dp[0][j]=0;
dp[i][0]=0;4.遍历顺序:
dp值从左上角递推而得
i:从上到下
j:从左至右class Solution {
public:bool isSubsequence(string s, string t) {//dp[i][j]:以s[i-1]结尾的字符串s,和以t[j-1]结尾的字符串t,相同子序列长度vector<vector<int>>dp(s.length()+1,vector<int>(t.length()+1));//完善dpfor(int i=1;i<s.length()+1;i++){for(int j=i;j<t.length()+1;j++){if(s[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=dp[i][j-1];}}return dp[s.length()][t.length()]==s.length();}
};双指针法:
创建两个索引指针sIndex、tIndex分别指向s和t,如果t[tIndex]==s[sIndex],那么两根指针同时后移;否则tIndex后移,直到sIndex扫完s
,恰好也符合子序列顺序。
class Solution {
public:bool isSubsequence(string s, string t) {int sIndex=0;//指向s字符的指针int tIndex=0;//指向t字符的指针while(sIndex<s.length()&&tIndex<t.length()){if(s[sIndex]==t[tIndex]){sIndex++;tIndex++;}else{tIndex++;}}//sIndex扫过的区域都是在t中以同样的顺序出现过的return sIndex==s.length();}
};37. LeetCode115. 不同的子序列
解读题意:从s中可以找出几个子序列恰好和t相同。s如何删除元素可以变成t
1.dp含义:
dp[i][j]:以s[i-1]结尾的字符串s中,以t[j-1]结尾的字符串t个数2.转移方程:
只有出现新字符时(下一轮循环)才会有未考虑的情况,对于新出现字符只有两种考虑(使用或不使用)
if(s[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1]+dp[i-1][j];//s[i-1]可使用也可不使用(模拟删除),两种情况总和。t无法删除元素
else dp[i][j]=dp[i-1][j];//不匹配,不用考虑s[i-1]3.初始化dp:
dp[0][j]=0;
dp[i][0]=1;
dp[0][0]=1;4.遍历顺序:
i:从上到下
j:从左到右class Solution {
public:int numDistinct(string s, string t) {//dp[i][j]:以s[i-1]结尾的字符串s中,以j[i-1]结尾的字符串t个数vector<vector<uint64_t>>dp(s.length()+1,vector<uint64_t>(t.length()+1));//初始化dpfor(int i=0;i<s.length()+1;i++){dp[i][0]=1;}for(int j=1;j<t.length()+1;j++){dp[0][j]=0;}//完善dpfor(int i=1;i<s.length()+1;i++){for(int j=1;j<t.length()+1;j++){if(s[i-1]==t[j-1])dp[i][j]=dp[i-1][j-1]+dp[i-1][j];else dp[i][j]=dp[i-1][j];}}return dp[s.length()][t.length()];}
};38. LeetCode583. 两个字符串的删除操作
思路:
二维数组,因为需要操作两个字符串1.dp含义:
dp[i][j]:让以word1[i-1]结尾的字符串word1和以word2[j-1]结尾的字符串word2相同的最少操作数
2.转移方程:
对于新字符word1[i-1]和word2[j-1]只有相同和不相同两种情况
if(word1[i-1]==word[j-1])dp[i][j]=dp[i-1][j-1];//保留这两字符可以减少两步删除操作
else dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+2);//二者选一个删除或都删除,取最小操作数
3.遍历顺序:
i:从上到下
j:从左到右
4.初始化dp:
dp[0][j]=j;//word1是空字符,word2必须删掉所有字符才能相同
dp[i][0]=i;class Solution {
public:int minDistance(string word1, string word2) {//dp[i][j]:让以word1[i-1]结尾的字符串word1和以word2[j-1]结尾的字符串word2相同的最少操作数vector<vector<int>>dp(word1.length()+1,vector<int>(word2.length()+1));//初始化dpfor(int i=0;i<=word1.length();i++){dp[i][0]=i;}for(int j=0;j<=word2.length();j++){dp[0][j]=j;}//完善dpfor(int i=1;i<=word1.length();i++){for(int j=1;j<=word2.length();j++){if(word1[i-1]==word2[j-1])dp[i][j]=dp[i-1][j-1];else dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+2));}}return dp[word1.length()][word2.length()];}
};也可以求最长公共子序列长度,然后经过计算得出结果。39. LeetCode72. 编辑距离
思路:
虽然题目说让word1变成word2,但也可以让word2变成word1。因为删除word1的字符,等效于在word2中添加字符,所以删除操作包含了添加操作1.dp含义:
dp[i][j]:让以word1[i-1]结尾的字符串word1和以word2[j-1]结尾的字符串word2相同的最少操作数
2.转移方程:
if(word1[i-1]==word2[j-1])dp[i][j]=dp[i-1][j-1];
else{dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);//删除,这二者已经包含了dp[i-1][j-1]+2dp[i][j]=min(dp[i][j],dp[i-1][j-1]+1);//替换
}
3.遍历顺序:
i:从上到下
j:从左到右
4.初始化dp:
dp[0][j]=j;
dp[i][0]=i;class Solution {
public:int minDistance(string word1, string word2) {//dp[i][j]:让以word1[i-1]结尾的字符串word1和以word2[j-1]结尾的字符串word2相同的最少操作数vector<vector<int>>dp(word1.length()+1,vector<int>(word2.length()+1));//初始化dpfor(int i=0;i<=word1.length();i++){dp[i][0]=i;}for(int j=0;j<=word2.length();j++){dp[0][j]=j;}//完善dpfor(int i=1;i<=word1.length();i++){for(int j=1;j<=word2.length();j++){if(word1[i-1]==word2[j-1])dp[i][j]=dp[i-1][j-1];else{dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);//删除,这二者已经包含了dp[i-1][j-1]+2dp[i][j]=min(dp[i][j],dp[i-1][j-1]+1);//替换}}}return dp[word1.length()][word2.length()];}
};相关文章:
:子序列、子数组问题)
LeetCode动态规划经典题目(九):子序列、子数组问题
目录 31. LeetCode674. 最长连续递增序列 32. LeetCode18. 最长重复子数组 33. LeetCode1143. 最长公共子序列 34. LeetCode1035. 不相交的线 35. LeetCode53. 最大子数组和 36. LeetCode392.判断子序列 37. LeetCode115. 不同的子序列 38. LeetCode583. 两个字符串的删…...

如何利用有限的数据发表更多的SCI论文?——利用ArcGIS探究环境和生态因子对水体、土壤和大气污染物的影响
SCI的写作和发表是科研人提升自身实力和实现自己价值的必要途径。“如何利用有限的数据发表更多的SCI论文?”是我们需要解决的关键问题。软件应用只是过程和手段,理解事件之间的内在逻辑和寻找事物之间的内在规律才是目的。如何利用有限的数据发表更多的…...
六【 SpringMVC框架】
一 SpringMVC框架 目录一 SpringMVC框架1.什么是MVC2.SpringMVC概述3.SpringMVC常见开发方式4.SpringMVC执行流程5.SpringMVC核心组件介绍6.快速构建Spring MVC程序✅作者简介:Java-小白后端开发者 🥭公认外号:球场上的黑曼巴 🍎个…...
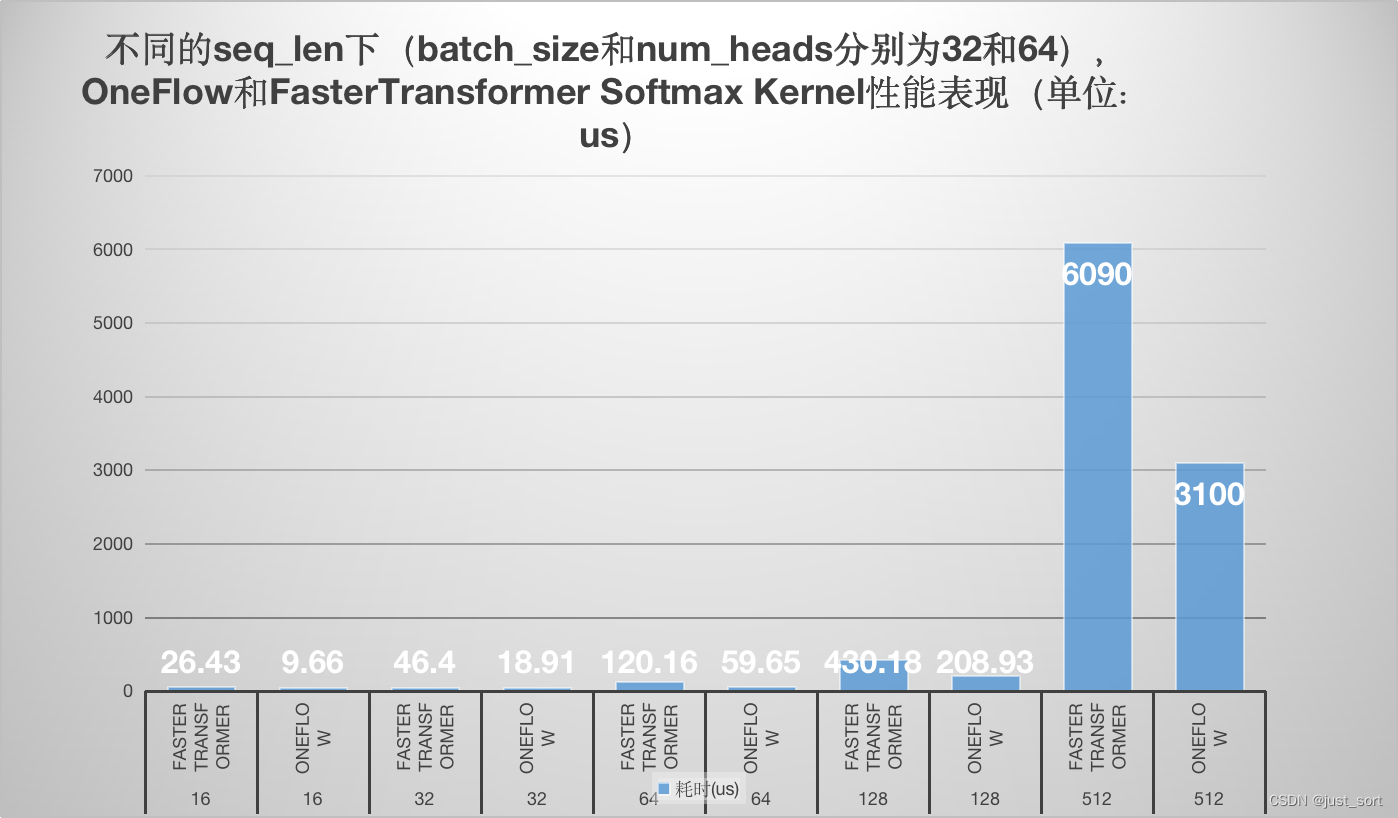
【BBuf的CUDA笔记】八,对比学习OneFlow 和 FasterTransformer 的 Softmax Cuda实现
0x1. OneFlow/FasterTransformer SoftMax CUDA Kernel 实现学习 这篇文章主要学习了oneflow的softmax kernel实现以及Faster Transformer softmax kernel的实现,并以个人的角度分别解析了原理和代码实现,最后对性能做一个对比方便大家直观的感受到onefl…...

python 类对象的析构释放代码演示
文章目录一、类的构造函数与析构函数二、代码演示1. 引用的更迭2. 只在函数内部的类对象三、函数内部返回的类对象1. 使用全局变量 引用 函数内部的类对象一、类的构造函数与析构函数 init 函数是python 类的构造函数,在创建一个类对象的时候,就会自动调…...
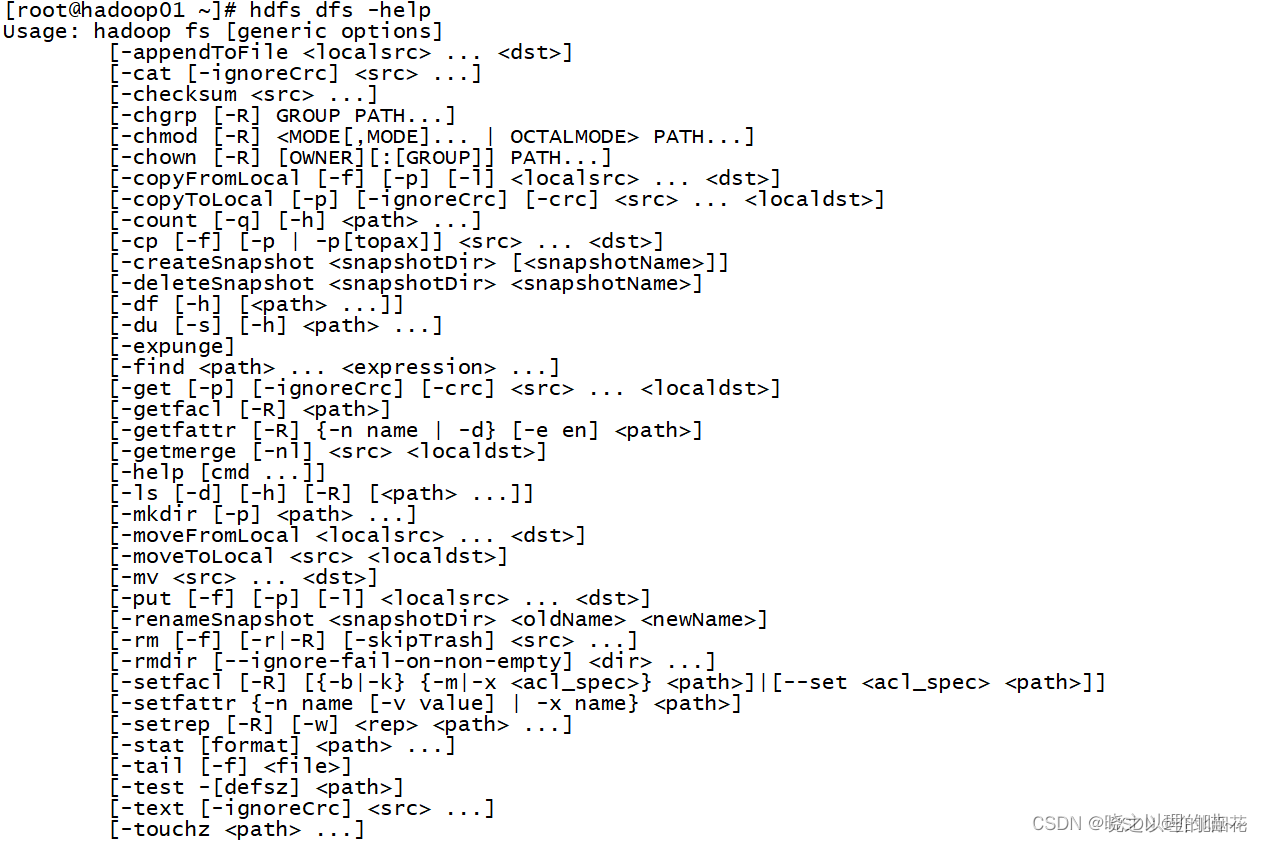
Hadoop Shell常用命令
Hadoop Shell命令在管理HDFS的时候还是比较常用的,Hadoop Shell命令与shell命令极为相似,但是方便查询,在这里总结分享,大家enjoy~~ 1,cat 语法格式:hadoop fs -cat URI [URI …] 含义:将路径…...

Android中级——色彩处理和图像处理
色彩处理 通过色彩矩阵处理 色彩矩阵介绍 图像的RGBA可拆分为一个4行5列的矩阵和5行1列矩阵相乘 其中4行5列矩阵即为ColorMatrix,可通过调整ColorMatrix间接调整RGBA 第一行 abcde 决定新的 R第二行 fghij 决定新的 G第三行 klmno 决定新的 G第四行 pqrst 决定新…...
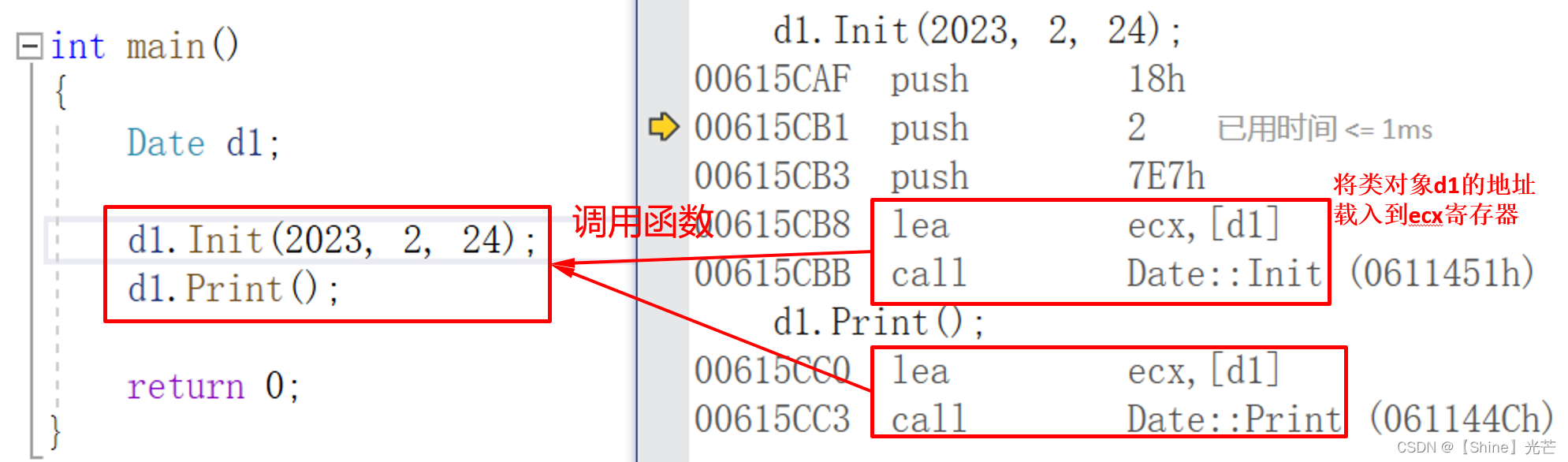
C++类和对象:类的定义、类对象的存储、this指针
目录 一. 对于面向过程和面向对象的认识 二. 类 2.1 struct关键字定义类 2.1.1 C语言中的struct关键字 2.1.2 C中的struct关键字 2.2 class关键字 2.1 使用class关键字定义类 三. 类的访问限定及封装 3.1 类的访问权限及访问限定符 3.1.1 访问权限 3.1.2 访问限定…...
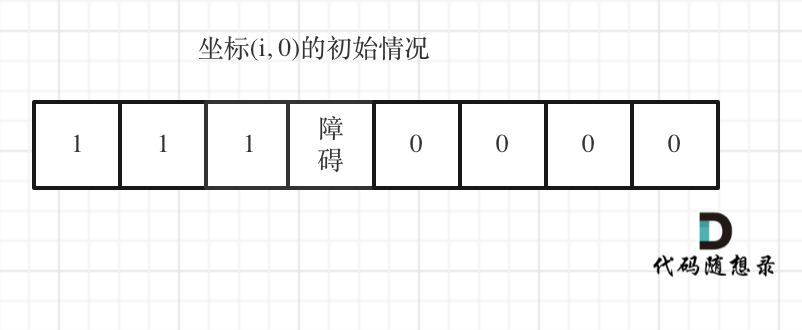
代码随想录算法训练营第三十九天 | 62.不同路径,63. 不同路径 II
一、参考资料不同路径https://programmercarl.com/0062.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84.html 视频讲解:https://www.bilibili.com/video/BV1ve4y1x7Eu不同路径 IIhttps://programmercarl.com/0063.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84II.htmlhttps://progr…...

数据库复习3
一. 简答题(共1题,100分) 1. (简答题) 存在数据库test,数据库中有如下表: 1.学生表 Student(Sno,Sname,Sage,Ssex) --Sno 学号,Sname 学生姓名,Sage 出生年月,Ssex 学生性别 主键Sno 2.教师表 Teacher(Tno,Tname) --T…...

顺序表的增删查改
数据结构 是数据存储的方式,对于不同的数据我们要采用不同的数据结构。就像交通运输,选用什么交通工具取决于你要运输的是人还是货物,以及它们的数量。 顺序存储结构 包括顺序表、链表、栈和队列等。 例如腾讯QQ中的好友列表,…...

jupyter matplotlib中文乱码解决
中文乱码可能有两种情况 1. matplotlib里面有中文字体 2. 没有中文字体 查看是否有中文字体: # 查询当前系统所有字体 from matplotlib.font_manager import FontManager import subprocessmpl_fonts = set(f.name for f in FontManager().ttflist)print(all font list get f…...
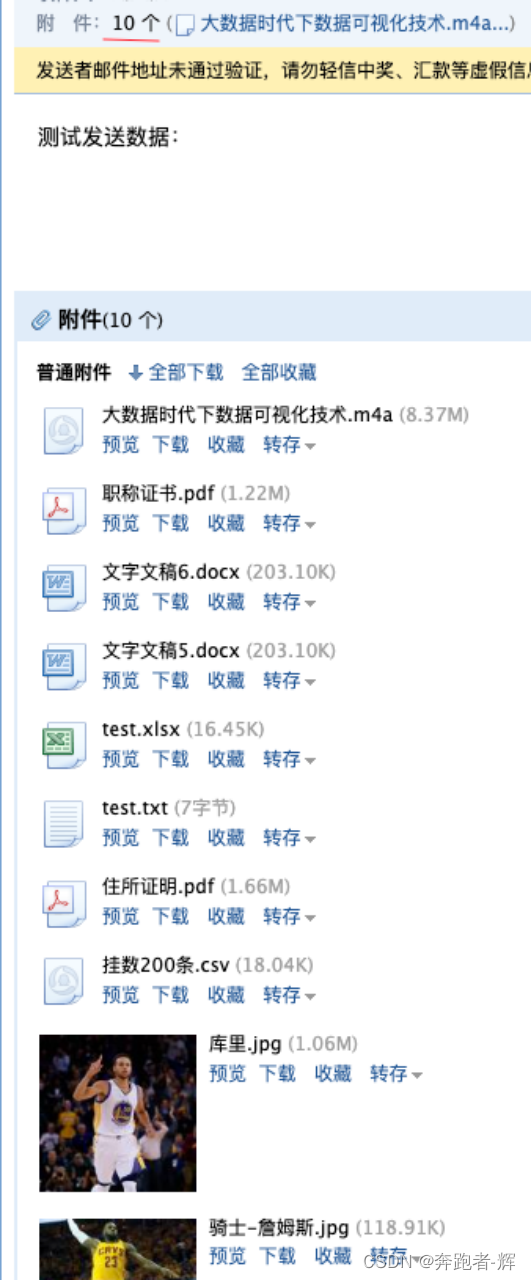
Smtplib之发邮件模块
目录 创建Smtp对象 Smtp类中的方法 MIME MIMEBase MIMEBase MIMEMultipart MIMEApplication MIMEAudio MIMEImage MIMEText 实例 texthtml格式 发送带图片附件的邮件 发送带附件的邮件 含多种格式 SMTP模块 SMTP 简单传输协议,它是一组用于由源…...

Android 适配手机和平板
一、屏幕适配限定符Android 系统加载应用资源时 , 会根据当前运行应用的设备的相关属性 , 如 : 屏幕尺寸 / 屏幕像素密度 / 宽高比 / 屏幕方向 等属性 , 加载不同的屏幕适配限定符目录下的资源 ;如 : 横竖屏切换时 , res/layout-land 目录中 , 存放的是横屏布局 , res/layout-p…...

时序预测 | MATLAB实现LSTM-SVR(长短期记忆神经网络-支持向量机)时间序列预测
时序预测 | MATLAB实现LSTM-SVR(长短期记忆神经网络-支持向量机)时间序列预测 目录时序预测 | MATLAB实现LSTM-SVR(长短期记忆神经网络-支持向量机)时间序列预测效果一览基本介绍模型介绍LSTM模型SVR模型LSTM-SVR模型程序设计参考资料致谢效果一览 基本介绍 本次运行测试环境MA…...
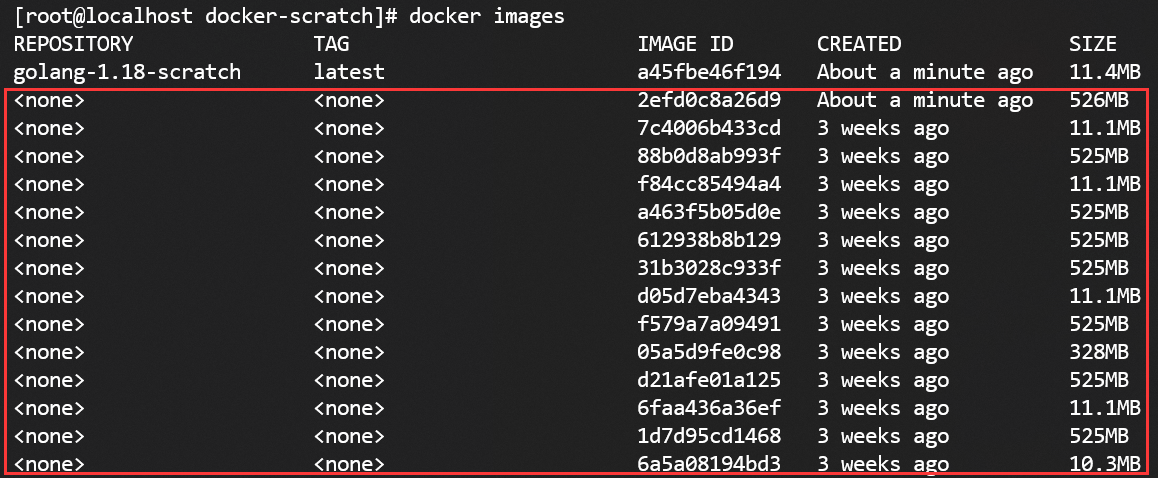
分阶段构建golang运行环境Dockerfile镜像
在开始这项工作之前大家可以先去看一下docker官方给出关于空镜像scratch的说明,采用官方简单的一句话就是:scratch是一个明确的空图像,特别是对于“从头开始”构建图像。分阶段构建镜像就会用到scratch这个空镜像,这样的好处是可以…...
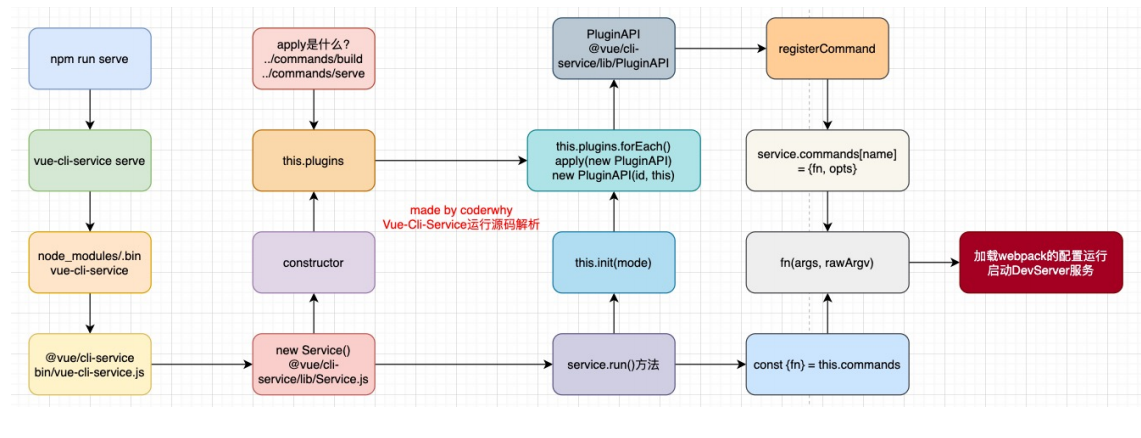
Vue-cli脚手架在做些什么(源码角度分析)
什么是Vue脚手架?在学习初期,我们的项目往往需要借助webpack、vite等打包工具配置Vue的开发环境,但是在真实开发中我们不可能每个项目从头来完成所有的webpack配置,这样显得开发的效率会大大的降低;所有的真实开发中&a…...
【Nginx】|入门连续剧——安装
作者:狮子也疯狂 专栏:《Nginx从入门到超神》 坚持做好每一步,幸运之神自然会降临在你的身上 目录一. 🦁 前言Ⅰ. 🐇 为啥我们要使用Nginx?二. 🦁 搭建流程Ⅰ. 🐇 环境准备Ⅱ. &…...

从0开始学python -38
Python3 面向对象-1 Python从设计之初就已经是一门面向对象的语言,正因为如此,在Python中创建一个类和对象是很容易的。本章节我们将详细介绍Python的面向对象编程。 如果你以前没有接触过面向对象的编程语言,那你可能需要先了解一些面向对…...
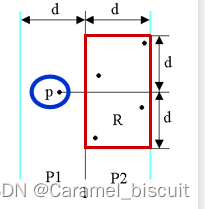
算法设计与分析期末考试复习(二)
分治法 将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。最好使子问题的规模大致相同。 分解(Divide):将一个难以直接解决的大问题,分割成一些规模较小的子…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...
