线性代数中涉及到的matlab命令-第一章:行列式
目录
1,逆序数
2,行列式定义和性质
2.1,常用特性及命令
2.2,求行列式
2.3,行列式的性质
2,行列式按行(列)展开
3,范德蒙德行列式
在学习线性代数过程中,发现同步使用MATLAB进行计算验证可以加深对概念的理解,并能掌握MATLAB的命令和使用方法;
使用的线性代数教材为同济大学出版的。
1,逆序数
没有找到对应的Matlab命令,但可以通过简单编程来进行求解;
2,行列式定义和性质
需要注意的是,在MATLAB中运算时直接使用矩阵表示行列式;

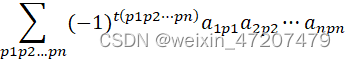
2.1,常用特性及命令
转置 B = A'

上三角、下三角行列式:
使用的Matlab命令,tril和triu

2.2,求行列式
det(A)
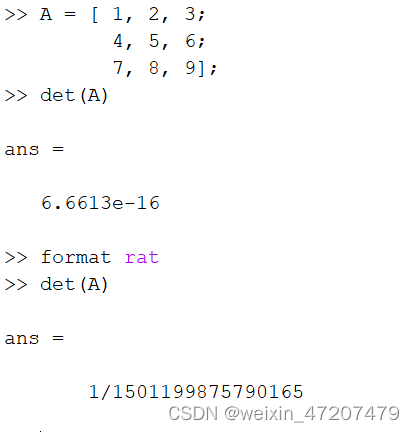
2.3,行列式的性质
以下为利用matlab的det命令对行列式的几种性质进行计算:
上三角矩阵的行列式为对角线元素的乘积:

对角矩阵行列式为对角线元素的乘积:

性质1,行列式和它转置后的行列式相等:

性质2,交换矩阵的两行(列),行列式变号:

推论,矩阵中存在相同的行或列,则行列式等于0(可以用上一条进行推倒):

性质3,矩阵的一行或列所有元素乘以k,其行列式也乘以k:

性质4,行列式中如果有两行(列)元素成比例,则行列式等于0:

性质5,

clc;A=[2 4 6 7;1 3 2 1;1 5 7 3;1 2 1 5];B=[2 4 2 7;1 3 2 1;1 5 3 3;1 2 0 5];C=[2 4 4 7;1 3 0 1;1 5 4 3;1 2 1 5];D_A = det(A)D_B = det(B)D_C = det(C)运行结果:
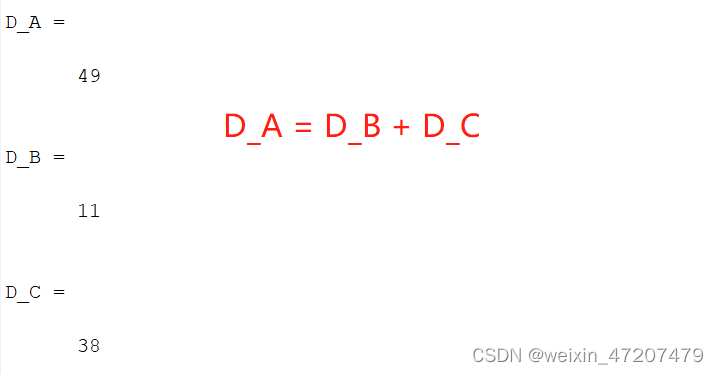
性质6,矩阵的一行或列加上另一行或列的k倍,行列式的值不变:

行列式性质例10证明,具体的证明请查阅教材:
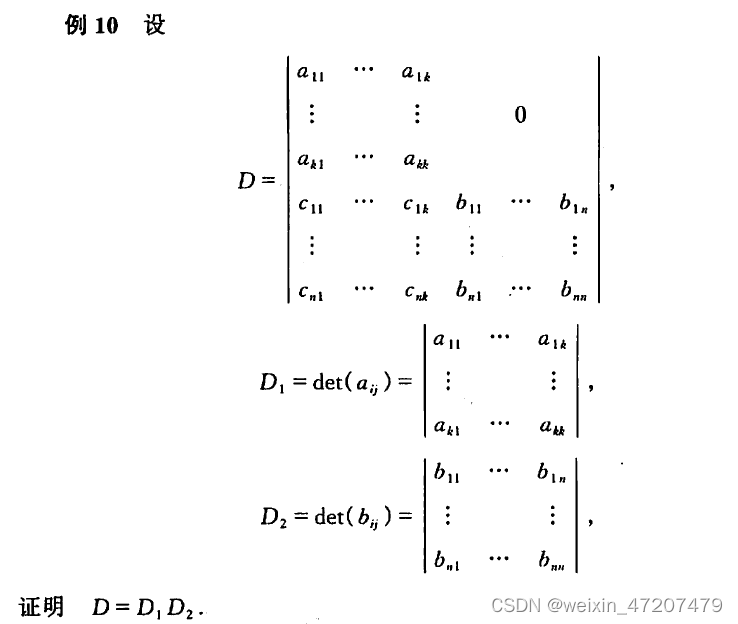
使用Matlab计算一个这样的实例:
clc;
a = [ 1 2;3 4];
b = [0 0 0;0 0 0];
c = [6 7;4 5;2 7];
d = [3 6 2;8 5 3;4 6 2];e = [a,b];
f = [c,d];A = [e;f]D_A = det(A)D_a = det(a)D_b = det(d)运行结果:
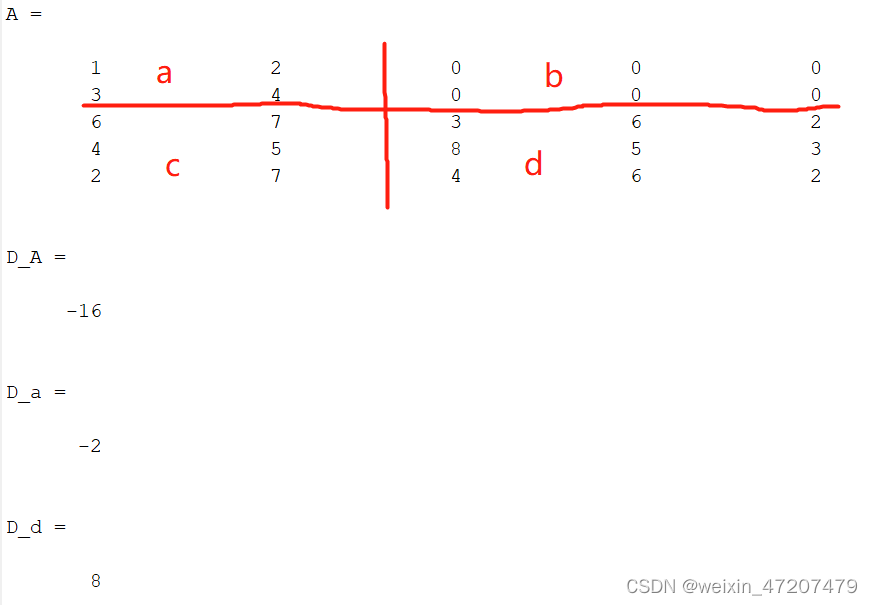
可见D(A) = D(a)*D(d)。
2,行列式按行(列)展开
余子式和代数余子式:

%求N(2,1)的余子式和代数余子式
clc;N = [3 6 2 5;8 5 3 7;4 6 2 9;5 7 4 1];N(2,:) = []; %把第二行划去
N(:,1) = []; %把第一列划去NM_21 = det(N) %余子式A_21 = (-1)^(2+1)*det(N) %代数余子式
运行结果:

 对上边引理计算一个对应的Matlab程序:
对上边引理计算一个对应的Matlab程序:
clc;A=[2 4 6 7;0 3 0 0;1 5 7 3;1 0 1 0]; %A的第二行除A(2,2)外全为0B = A;B(2,:) = [];
B(:,2) = []; %A的第二行第二列的余子式D_A = det(A)%D_B = det(B)
D_B = (-1)^(2+2) * det(B) %A的第二行第二列的代数余子式运行结果与引理相符:
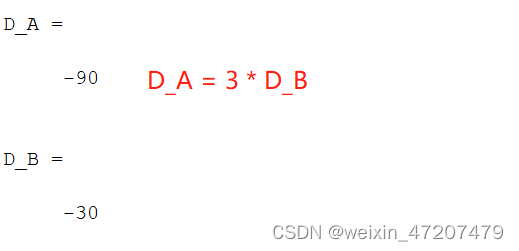

对上边定理计算一个对应的Matlab程序:
clc;A=[2 4 6 7;1 3 2 1;1 5 7 3;1 0 1 0];B = A;
C = A;
D = A;
E = A;B(2,:) = [];
B(:,1) = []; %A的第二行第一列的余子式C(2,:) = [];
C(:,2) = []; %A的第二行第二列的余子式D(2,:) = [];
D(:,3) = []; %A的第二行第三列的余子式E(2,:) = [];
E(:,4) = []; %A的第二行第四列的余子式D_A = det(A)D_B21 = (-1)^(2+1) * det(B) * A(2,1) %A的第二行第一列的代数余子式 * 第二行第一列元素D_C22 = (-1)^(2+2) * det(C) * A(2,2) %A的第二行第二列的代数余子式 * 第二行第二列元素D_D23 = (-1)^(2+3) * det(D) * A(2,3) %A的第二行第三列的代数余子式 * 第二行第三列元素D_E24 = (-1)^(2+4) * det(E) * A(2,4) %A的第二行第四列的代数余子式 * 第二行第四列元素运行结果与定理相符:

3,范德蒙德行列式
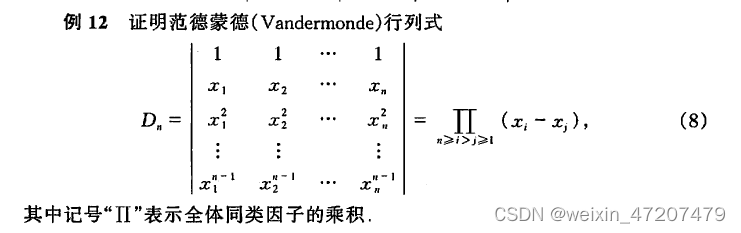 以下程序产生一个范德蒙德行列式并分别用det和
以下程序产生一个范德蒙德行列式并分别用det和![]() 的方式计算行列式的值:
的方式计算行列式的值:
clc;v = 2:0.5:4;A = vander(v);A = fliplr(A);A = A'D_A = det(A)tot =(A(2,5)-A(2,4)) * (A(2,5)-A(2,3)) * (A(2,5)-A(2,2)) * (A(2,5)-A(2,1)) * (A(2,4)-A(2,3)) * (A(2,4)-A(2,2)) * (A(2,4)-A(2,1)) *...(A(2,3)-A(2,2)) * (A(2,3)-A(2,1)) * (A(2,2)-A(2,1))运行结果:

上图中第二个计算结果是通过![]() 方式计算。
方式计算。
相关文章:
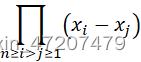
线性代数中涉及到的matlab命令-第一章:行列式
目录 1,逆序数 2,行列式定义和性质 2.1,常用特性及命令 2.2,求行列式 2.3,行列式的性质 2,行列式按行(列)展开 3,范德蒙德行列式 在学习线性代数过程中&#…...

QT编程,QT内存管理、信号与槽、
目录 一、QT工具 二、QT内存管理 三、信号与槽 1、信号与槽特点 2、信号 3、槽函数 4、连接 5、发送信号 6、取消连接 一、QT工具 1、Qt Designer:界面设计编辑工具 2、Qt Assistant: Qt技术文档浏览器 3、Qt Linguist: 国际化语言翻译工具 4、…...
springcloud之项目实战环境准备
写在前面 为了更好的学习springcloud,我们来一起开发一个实战项目,加深理解。 1:项目介绍 在开始项目实战之前先来做一个整体的项目介绍,从而能够让对项目的整体架构和模板有一个比较清晰的认知。 大家都知道双11,…...
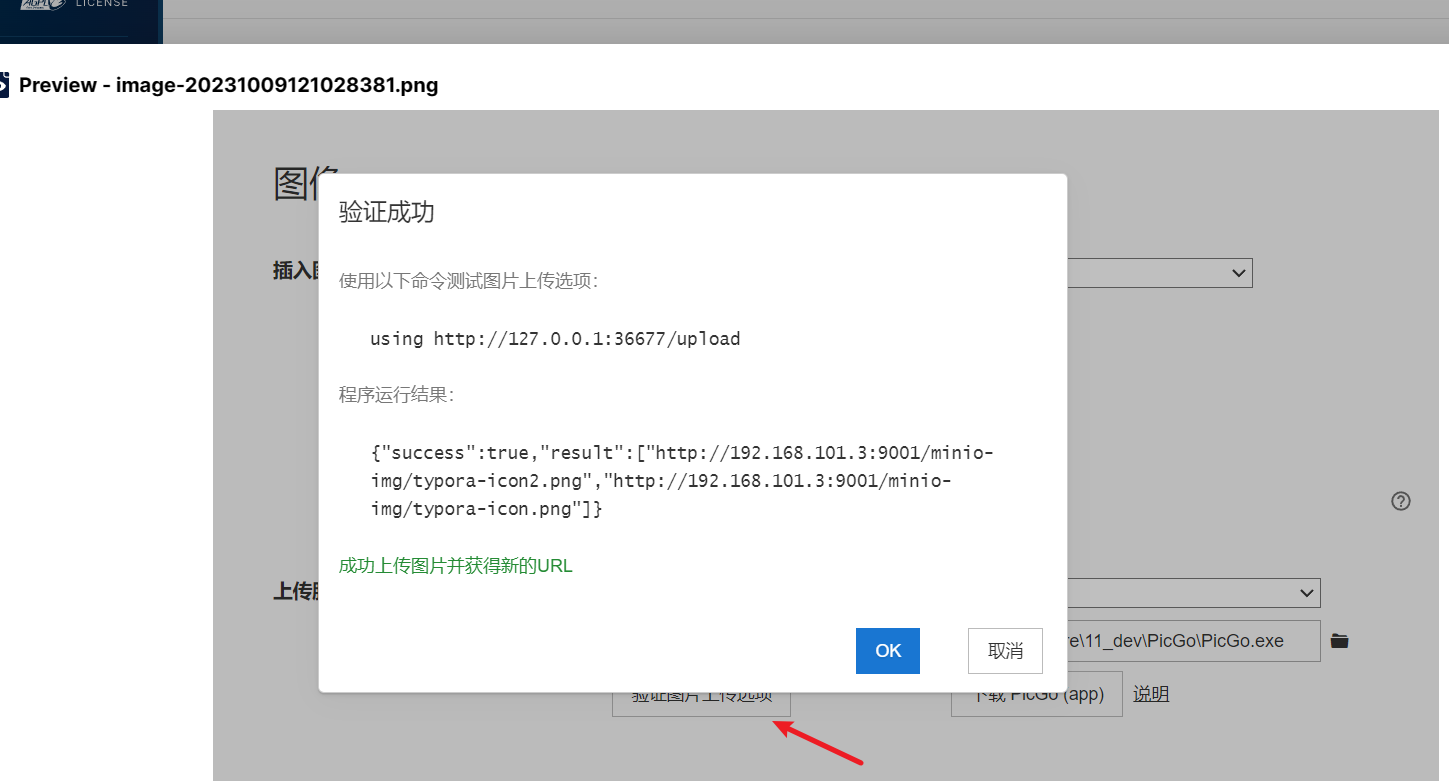
Linux 部署 MinIO 分布式对象存储 配置为 typora 图床
前言 MinIO 是一款高性能的对象存储系统,它可以用于大规模的 AI/ML、数据湖和数据库工作负载。它的 API 与Amazon S3 云存储服务完全兼容,可以在任何云或本地基础设施上运行。MinIO 是开源软件,也提供商业许可和支持 MinIO 的特点有&#x…...
)
JVM Optimization Learning(四)
目录 一、调优 1、基础概念 2、什么是调优? 3、调优,从规划开始 4、调优案例 一、调优 1、基础概念 吞吐量:用户代码执行时间 /(用户代码执行时间 垃圾回收时间) 响应时间:STW越短,响应…...

新华三辅导笔记 2023/10/9-2023/10/13
新华三辅导笔记 一、需要用到的软件二、计算机网络概述1、计算机网络的定义和基本功能(1)什么是计算机网络(2)计算机网络的基本功能 2、(1)局域网、城域网和广域网(范围划分)&#x…...

边坡安全监测系统的功能优势
随着科技的进步,边坡安全监测系统在各种工程项目中发挥着越来越重要的作用。这款系统通过实时监测垂直、水平位移数据,以折线图的方式显示在监控平台中,为工程人员提供了直观、便捷的监控工具,从而能够及时掌握边坡稳定状况&#…...

【架构】研发高可用架构和系统设计经验
研发高可用架构和系统设计经验 从研发规范层面、应用服务层面、存储层面、产品层面、运维部署层面、异常应急层面这六大层面去剖析一个高可用的系统需要有哪些关键的设计和考虑。 一、高可用架构和系统设计思想 1.可用性和高可用概念 可用性是一个可以量化的指标,计算的公…...
Linux线程安全
线程安全 Linux线程互斥进程线程间的互斥相关背景概念互斥量mutex互斥量的接口互斥量实现原理探究 可重入VS线程安全概念常见的线程不安全的情况常见的线程安全的情况常见的不可重入的情况常见的可重入的情况可重入与线程安全联系可重入与线程安全区别 常见锁概念死锁死锁的四个…...

Windows安装Node.js
1、Node.js介绍 ①、Node.js简介 Node.js是一个开源的、跨平台的JavaScript运行环境,它允许开发者使用JavaScript语言来构建高性能的网络应用程序和服务器端应用。Node.js的核心特点包括: 1. 事件驱动: Node.js采用了事件驱动的编程模型,通…...

想要开发一款游戏, 需要注意什么?
开发一款游戏是一个复杂而令人兴奋的过程。游戏开发是指创建、设计、制作和发布电子游戏的过程。它涵盖了从最初的概念和创意阶段到最终的游戏发布和维护阶段的各个方面。 以下是一些需要注意的关键事项: 游戏概念和目标: 确定游戏开发的核心概念和目标…...
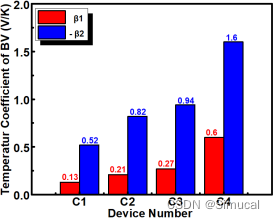
横向AlGaN/GaN基SBD结构及物理模型数据库的开发
GaN基功率器件凭借其临界电场高、电子饱和漂移速度大、热导率高等优良性能在大功率快充、充电桩、新能源汽车等领域具备广泛应用空间。为进一步助推半导体高频、高功率微电子器件的发展进程,天津赛米卡尔科技有限公司技术团队依托先进的半导体TCAD仿真平台成功开发出…...

使用安卓Termux+Hexo,手机也能轻松搭建个人博客网站
文章目录 前言1.安装 Hexo2.安装cpolar3.远程访问4.固定公网地址5.结语 前言 Hexo 是一个用 Nodejs 编写的快速、简洁且高效的博客框架。Hexo 使用 Markdown 解析文章,在几秒内,即可利用靓丽的主题生成静态网页。 下面介绍在Termux中安装个人hexo博客并…...

Spring在业务中常见的使用方式
目录 通过IOC实现策略模式 通过AOP实现拦截 通过Event异步解耦 通过Spring管理事务 通过IOC实现策略模式 很多时候,我们需要对不同的场景进行不同的业务逻辑处理举个例子,譬如不同的场景需要不同支付方式,普通的逻辑是使用if-else&#x…...

PyTorch 深度学习实战
文章目录 前言1. 环境安装1.Anaconda2.pytorch cuda 环境3.测试 前言 1. 环境安装 1.Anaconda 可以参考这里:Anaconda学习 2.pytorch cuda 环境 我是按照下面的博客一步步完成,亲测有效 Pytorch安装教程(最全最详细版) 我的…...
学生用RockyLinux9.2模板虚拟机说明
“RockyLinux9.2”模板虚拟机下载地址 链接:https://pan.baidu.com/s/1xcakszIQ7Kp9Nw_NA9Znlg?pwdqzmm 提取码:qzmm 1.模板机是基于“Rocky-9.2-x86_64-minimal.iso”安装 2.模板机是2023.10.10执行dnf update && dnf upgrade更新和升级软件…...

BUUCTF reverse3 1
先运行下 看来是输入正确的flag 使用DIE查看文件 看起来没有壳,直接IDA打开 shift F12查找字符串 一路跟踪 到汇编窗口后F5 这里对Destination和Str2进行比较,Str2有值那么Str2就是经过上面一系列处理之后得到的内容了 继续分析上面的代码 根据…...

关于webWorker未解问题
今天尝试学习webworker,尝试在vue3项目里面使用 使用的就是常规方法,使用worker-loader,加上在vue.config.js内部添加配置 使用完发现问题 如图所见,该worker仅仅配置点击后传输字符串"1",并在worker内部打印,发现打印不出来 但是仅仅只是将引入的文件换个名字 …...
自然语言处理(NLP)的开发框架
自然语言处理(NLP)领域有许多开源的框架和库,用于处理文本数据和构建NLP应用程序。以下是一些常见的NLP开源框架及其特点,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合…...

Spring Boot与Kubernetes结合:构建高可靠、高性能的微服务架构
Spring Boot和Kubernetes(K8s)是当今非常热门的技术,它们的结合可以帮助开发者更高效地构建、部署和管理应用程序。本文将详细介绍Spring Boot和Kubernetes的主要特点,以及它们结合使用的优势。 一、Spring Boot的特点 Spring B…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
