【完整】UR机械臂逆运动学求解过程及c++代码实现
有任何问题请在评论区留言,我尽可能的回复大家
一. 逆运动学的求解需要以下数学运算
- 利用DH参数得到每个关节的变换矩阵;
- 利用变换矩阵求出机械臂整个链的变换矩阵;
- 求出末端位姿;
- 利用已知末端位姿和整个链的变换矩阵,通过逆运动学方程来求解关节角度;
- 根据需求选解。
二. 代码实现过程
- 利用DH参数得到每个关节的变换矩阵:
Eigen::Matrix4d DH(double a, double d, double alpha, double theta) {Eigen::Matrix4d T;T << cos(theta), -sin(theta)*cos(alpha), sin(theta)*sin(alpha), a*cos(theta),sin(theta), cos(theta)*cos(alpha), -cos(theta)*sin(alpha), a*sin(theta),0, sin(alpha), cos(alpha), d,0, 0, 0, 1;return T;
}
- 利用变换矩阵求出机械臂整个链的变换矩阵:
Eigen::Matrix4d T_0e = Eigen::Matrix4d::Identity(4,4);
for (int i = 0; i < n; i++) {T_0e = T_0e * DH(a[i], d[i], alpha[i], theta[i]);
}
- 求出末端位姿:
Eigen::Matrix4d T_ee;
T_ee << 0.5938, -0.7381, 0.3254, 0.4494,0.8038, 0.5531, 0.2194, -0.1957,-0.0332, 0.3868, 0.9214, 0.6733,0, 0, 0, 1;
- 然后利用已知末端位姿和整个链的变换矩阵,通过逆运动学方程来求解关节角度。
三. 逆运动学方程求解关节角度
逆运动学方程求解关节角度是一个非线性方程组,有多种方法求解,如解析解、数值解等。这里以数值解的方法为例,介绍如何用c++代码实现逆运动学方程的求解。
- 实现齐次变换矩阵的逆变换:
Eigen::Matrix4d invT(const Eigen::Matrix4d& T) {Eigen::Matrix4d invT;invT.block<3,3>(0,0) = T.block<3,3>(0,0).transpose();invT.block<3,1>(0,3) = -invT.block<3,3>(0,0)*T.block<3,1>(0,3);invT.block<1,4>(3,0) << 0, 0, 0, 1;return invT;
}
- 实现逆运动学方程:
Eigen::Matrix<double,6,1> inverseKinematics(const Eigen::Matrix4d& T_ee, const Eigen::Matrix4d T_0e, const Eigen::Vector3d& p_e,const Eigen::Vector3d& o_x,const Eigen::Vector3d& o_y,const Eigen::Vector3d& o_z) {Eigen::Matrix<double,6,1> theta;Eigen::Matrix4d T_0e_inv = invT(T_0e);Eigen::Matrix4d T_ee_0 = T_ee * T_0e_inv;Eigen::Vector3d p_0 = T_ee_0.block<3,1>(0,3);Eigen::Vector3d o_z_0 = T_0e_inv.block<3,3>(0,0) * o_z;Eigen::Vector3d o_y_0 = T_0e_inv.block<3,3>(0,0) * o_y;Eigen::Vector3d o_x_0 = T_0e_inv.block<3,3>(0,0) * o_x;// 具体实现逆运动学方程,这里省略return theta;
}
其中逆运动学方程的计算的详细过程如下:
● 求解末端位置p和姿态R的关于机器人的参考坐标系的坐标。
● 根据UR10机械臂的末端位置和姿态,计算关节角度。
实现逆运动学方程的代码,它计算出的结果是一个长度为6的Eigen向量,代表6个关节的角度:
#include <Eigen/Dense>
#include <cmath>Eigen::Matrix<double, 6, 1> inverseKinematics(const Eigen::Matrix4d& T_ee, const Eigen::Matrix4d T_0e, const Eigen::Vector3d& p_e,const Eigen::Vector3d& o_x,const Eigen::Vector3d& o_y,const Eigen::Vector3d& o_z)
{Eigen::Matrix<double, 6, 1> joint_angles;Eigen::Vector3d p_0e = T_0e.block<3,3>(0,0).transpose() * (p_e - T_0e.col(3).head<3>());double c5 = T_ee(2,2);double s5 = sqrt(1 - c5*c5);joint_angles(4) = atan2(s5, c5);joint_angles(5) = atan2(-T_ee(0,2), T_ee(1,2));joint_angles(3) = atan2(T_ee(2,1)/s5, T_ee(2,0)/s5);double s3 = sin(joint_angles(3));double c3 = cos(joint_angles(3));joint_angles(0) = atan2((p_0e(1)*s3 - p_0e(2)*c3) / s5, p_0e(0) - (p_0e(1)*c3 + p_0e(2)*s3) * c5);joint_angles(2) = atan2((p_0e(1)*c3 + p_0e(2)*s3) / c5, p_0e(0) - p_0e(1)*s3 + p_0e(2)*c3);joint_angles(1) = atan2(o_y(0), o_x(0));return joint_angles;
}
根据这个计算流程,将步骤 2 中省略的逆运动学方程具体实现的代码补充上:
Eigen::Matrix<double,6,1> inverseKinematics(const Eigen::Matrix4d& T_ee, const Eigen::Matrix4d T_0e, const Eigen::Vector3d& p_e,const Eigen::Vector3d& o_x,const Eigen::Vector3d& o_y,const Eigen::Vector3d& o_z) {Eigen::Matrix<double,6,1> theta;Eigen::Matrix4d T_0e_inv = invT(T_0e);Eigen::Matrix4d T_ee_0 = T_ee * T_0e_inv;Eigen::Vector3d p_0 = T_ee_0.block<3,1>(0,3);Eigen::Vector3d o_z_0 = T_0e_inv.block<3,3>(0,0) * o_z;Eigen::Vector3d o_y_0 = T_0e_inv.block<3,3>(0,0) * o_y;Eigen::Vector3d o_x_0 = T_0e_inv.block<3,3>(0,0) * o_x;
// 逆运动学方程的具体实现double q1, q2, q3, q4, q5, q6;double d = p_e(2) - p_0(2);q1 = atan2(p_0(1), p_0(0));double c2 = (pow(p_0(0), 2) + pow(p_0(1), 2) - pow(d, 2) - pow(o_x_0(2), 2)) / (2 * o_x_0(2) * sqrt(pow(p_0(0), 2) + pow(p_0(1), 2) - pow(d, 2)));q2 = atan2(sqrt(1-pow(c2, 2)), c2);q3 = atan2(o_z_0(2), -o_x_0(0) * sin(q2) + o_x_0(2) * cos(q2));double s4 = -o_y_0(2) * cos(q2) - o_y_0(0) * sin(q2) * sin(q3) + o_y_0(1) * sin(q2) * cos(q3);double c4 = o_x_0(0) * cos(q3) + o_x_0(1) * sin(q3) + o_x_0(2) * sin(q2);q4 = atan2(s4, c4);double s5 = o_x_0(0) * cos(q3) * sin(q4) + o_x_0(1) * sin(q3) * sin(q4) + o_x_0(2) * cos(q4);double c5 = o_y_0(0) * cos(q3) * cos(q4) + o_y_0(1) * sin(q3) * cos(q4) - o_y_0(2) * sin(q4);q5 = atan2(-s5, c5);double s6 = -o_x_0(0) * sin(q3) + o_x_0(1) * cos(q3);double c6 = o_y_0(0) * cos(q3) * cos(q5) + o_y_0(1) * sin(q3) * cos(q5) - o_y_0(2) * sin(q5);q6 = atan2(s6, c6);theta << q1, q2, q3, q4, q5, q6;return theta;
}
上面代码中的逆运动学方程的返回值 theta 可能会有多组解(UR机械臂通常为8组解),但是通常情况下仅返回一组最合适的解,因为它对应的正运动学方程只能够求出一组解。如果机器人的关节范围限制了某些解的取值范围,则需要在代码中加入关节范围限制的判断,以保证返回的解在关节范围内。
在当前代码中并没有对多组解进行选取的部分,所以该代码中直接返回的是求得的一组解。因为选取某一组解的方式取决于你所实现的逆运动学算法以及实际的应用需求,对于不同的需求,还需要对代码进行进一步的修改以实现选取一组合法的解的功能。
对于选解我在这里举一个例子:机械臂六个关节角度均有最大和最小的限制。
那么选解的代码可以写为:
if (q1 < q1_min) {q1 = q1 + 2 * M_PI;}if (q1 > q1_max) {q1 = q1 - 2 * M_PI;}// 根据需求,确定q2的取值范围if (q2 < q2_min) {q2 = q2_min;}if (q2 > q2_max) {q2 = q2_max;}// 根据需求,确定q3的取值范围if (q3 < q3_min) {q3 = q3_min;}if (q3 > q3_max) {q3 = q3_max;}// 根据需求,确定q4的取值范围if (q4 < q4_min) {q4 = q4_min;}if (q4 > q4_max) {q4 = q4_max;}// 根据需求,确定q5的取值范围if (q5 < q5_min) {q5 = q5_min;}if (q5 > q5_max) {q5 = q5_max;}// 根据需求,确定q6的取值范围if (q6 < q6_min) {q6 = q6_min;}if (q6 > q6_max) {q6 = q6_max;}theta << q1, q2, q3, q4, q5, q6;return theta;
相关文章:

【完整】UR机械臂逆运动学求解过程及c++代码实现
有任何问题请在评论区留言,我尽可能的回复大家 一. 逆运动学的求解需要以下数学运算 利用DH参数得到每个关节的变换矩阵;利用变换矩阵求出机械臂整个链的变换矩阵;求出末端位姿;利用已知末端位姿和整个链的变换矩阵,…...

68. Python的相对路径
68. Python的相对路径 文章目录68. Python的相对路径1. 知识回顾2. 什么是相对路径3. 相对路径的语法4. 查看相对路径的方法5. 写出所有txt文件的相对路径5.1 同目录5.2 上级目录6. 用相对路径读取txt文件6.1 读取旅游.txt6.2 读取旅游经费.txt6.3 读取笔记.txt和new.txt6.4 读…...
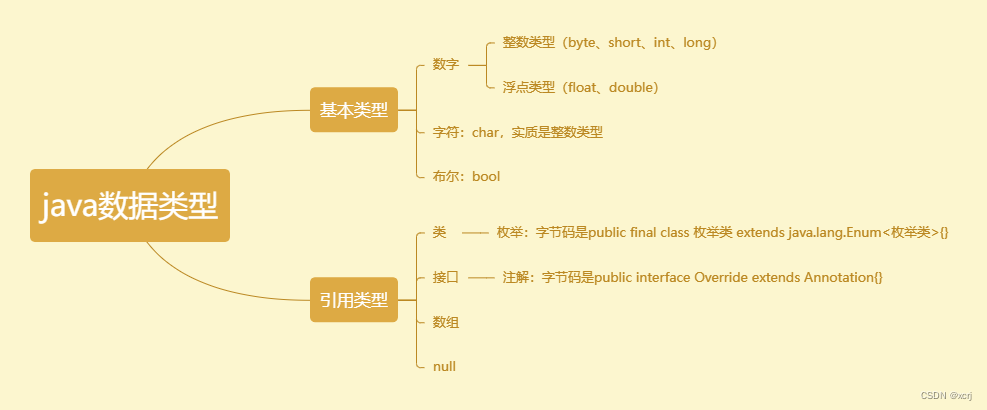
java数据类型
数据类型 类型分类,存储范围,字面量,默认值,类型转换 类型分类 存储范围 数据类型字节数表示范围byte1-128~127short2-32768~32767,正负3万左右int4-2147483648~2147483647,正负21亿左右long8-922337203…...

Kotlin 替换非空断言的几种方式
Kotlin 出现断言的两种情形 IDE java 与 kotlin 自动转换时,自动添加非空断言的代码Smart Cast 失效 代码展示: class JavaConvertExample {private var name: String? nullfun init() {name ""}fun foo() {name null;}fun test() {if (…...
2023年了,来试试前端格式化工具
在大前端时代,前端的各种工具链穷出不断,有eslint, prettier, husky, commitlint 等, 东西太多有的时候也是trouble😂😂😂,怎么正确的使用这个是每一个前端开发者都需要掌握的内容,请上车🚗&…...

spring cloud 企业工程项目管理系统源码+项目模块功能清单
工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和查看用户角色 4、菜单管理:实现对系统菜单的增删改查操…...

TCP分片解析
本文目录什么是IP分片为什么会产生IP分片为什么要避免IP分片如何避免IP分片什么是IP分片 IP协议栈将TCP/UDP传输层要求它发送的,但长度大于发送端口MTU的一个数据包,分割成多个IP报文后分多次发送。这些分成多次发送的多个IP报文就是IP分片。 为什么会…...
开发了一款基于 Flask 框架的在线电影网站系统(附 Python 源码)
文章目录前言项目介绍源码获取运行环境安装依赖库项目截图首页展示图视频展示页视频播放页后台管理页整体架构设计图项目目录结构图前台功能模块图后台功能模块图本地运行图前言 今天我给大家分享的是基于 Python 的 Flask 框架开发的在线电影网站系统,大家平时需要…...

如何获得CSM--敏捷教练证书
1、什么是CSM?CSM即Certified Scrum Master,Scrum Master负责确保所有人都能正确地理解并实施Scrum,确保Scrum团队遵循Scrum的理论、实践和规则。Scrum Master是Scrum团队中的服务型领导,帮助Scrum团队外的人员了解他们如何与Scrum团队交互是…...
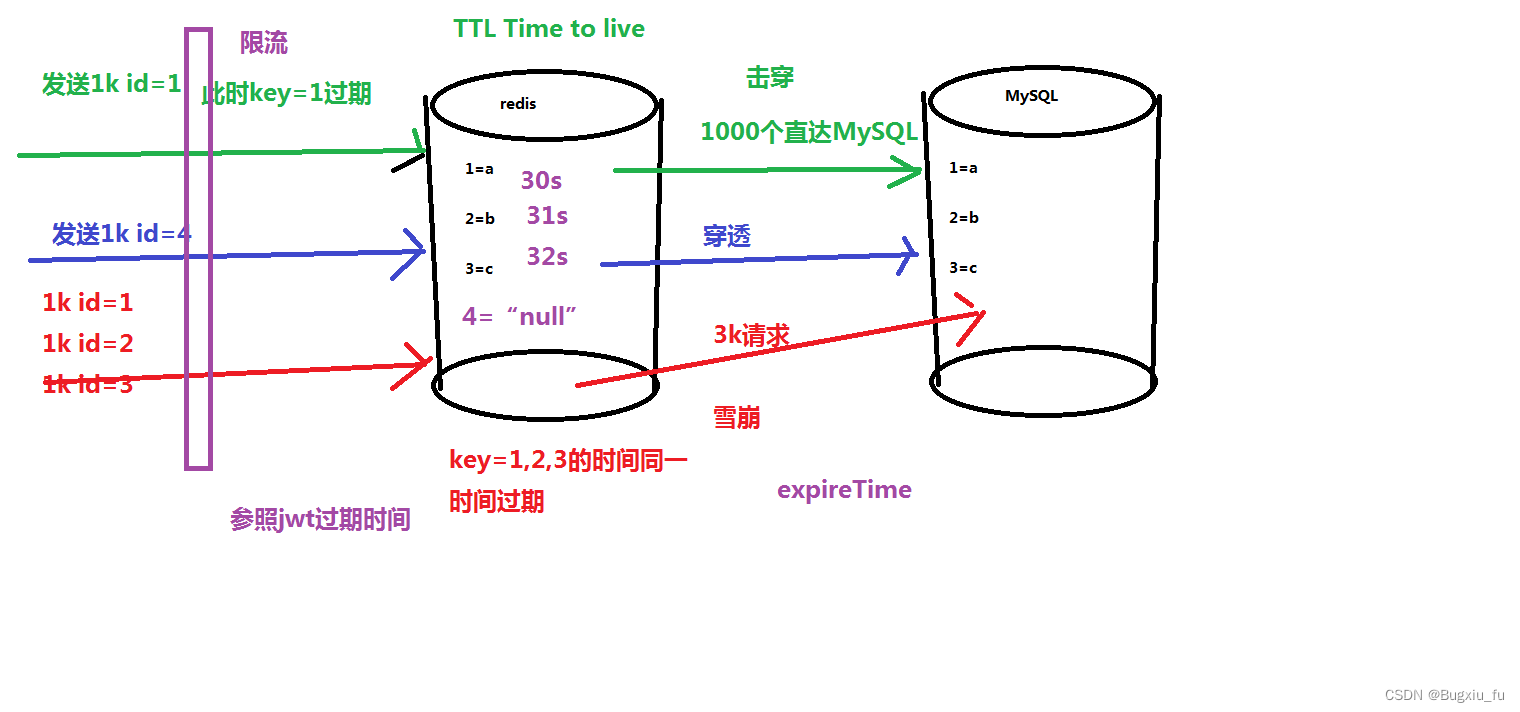
Java面试数据库
目录 一、关系型数据库 数据库权限 表设计及创建 表数据相关 数据库架构优化 二、非关系型数据库 redis 今天给大家稍微整理了一下,内容有数据表设计的三大范式原则、sql查询如何优化、redis数据的击穿、穿透、雪崩等...,以及相关的面试题࿰…...

关于进行vue-cli过程中的解决错误的问题
好久没发文章了,直到今天终于开始更新了,最近想进军全端,准备学习下vue,但是这东西真的太难了,我用了一天的时间来解决在配置中遇到的问题!主要问题:cnpm文件夹和vue-cli文件夹的位置不对并且vu…...

Rockchip Linux USB Gadget
一:概述 USB Gadget 是运行在 USB Peripheral 上配置 USB 功能的子系统,正常可被枚举的 USB 设备至少有 3 层逻辑层,有些功能还会在用户空间多跑一层逻辑代码。Gadget API 就是具体功能和硬件底层交互的中间层。从上到下,逻辑层分布为: USB Controller: USB上最底层的软…...
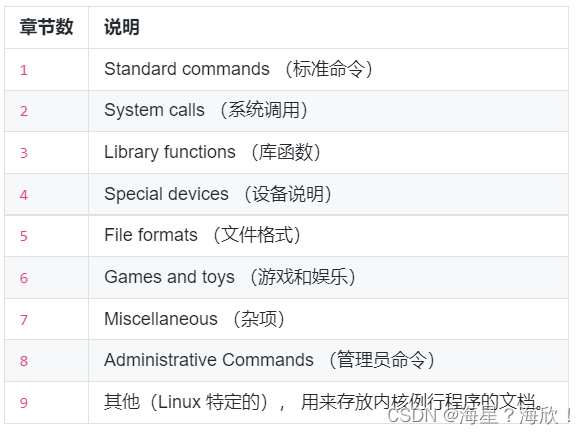
Linux -文件系统操作与帮助命令
1、Linux -文件系统操作 df — 查看磁盘的容量 df -h —以人类可以看懂的方式显示磁盘的容量,易读 du 命令查看目录的容量 # 默认同样以块的大小展示 du # 加上 -h 参数,以更易读的方式展示 du -h-d 参数指定查看目录的深度: # 只查看 1…...

UMI 创建react目录介绍及配置
UMI 生成react项目目录介绍及配置 react项目目录介绍umi多种配置方案运行时配置app.ts 的使用 1、umi创建的项目目录大致如下 ├─package.json 配置依赖以及启动打包所需的命令 ├─.umirc.ts 配置文件,包含 umi 内置功能和插件的配置 ├── dist 打包后生成的…...
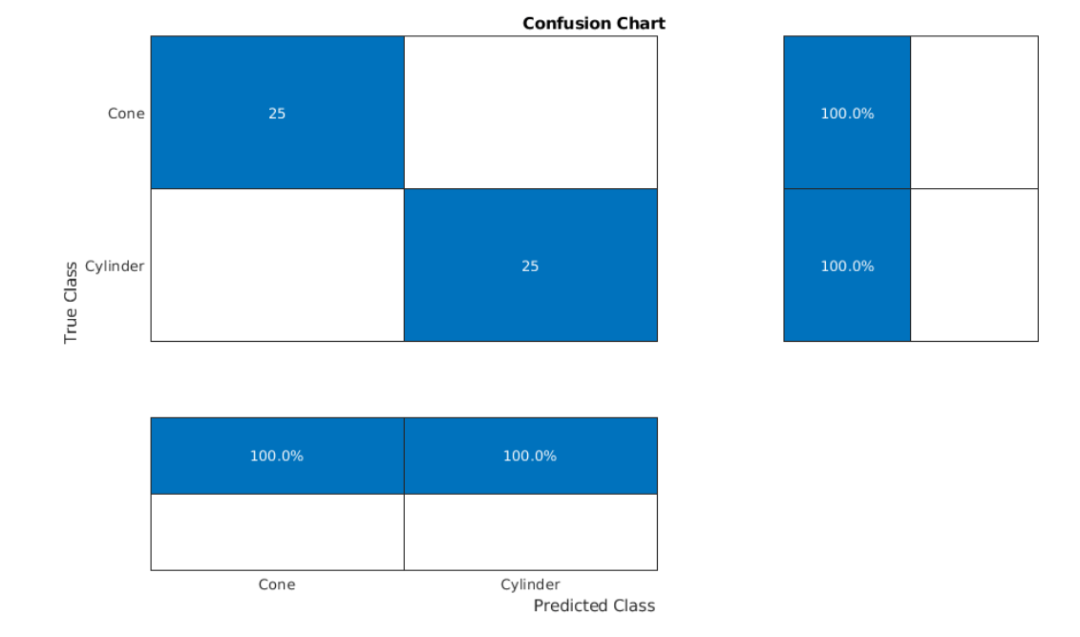
基于matlab使用机器学习和深度学习进行雷达目标分类
一、前言此示例展示了如何使用机器学习和深度学习方法对雷达回波进行分类。机器学习方法使用小波散射特征提取与支持向量机相结合。此外,还说明了两种深度学习方法:使用SqueezeNet的迁移学习和长短期记忆(LSTM)递归神经网络。请注…...
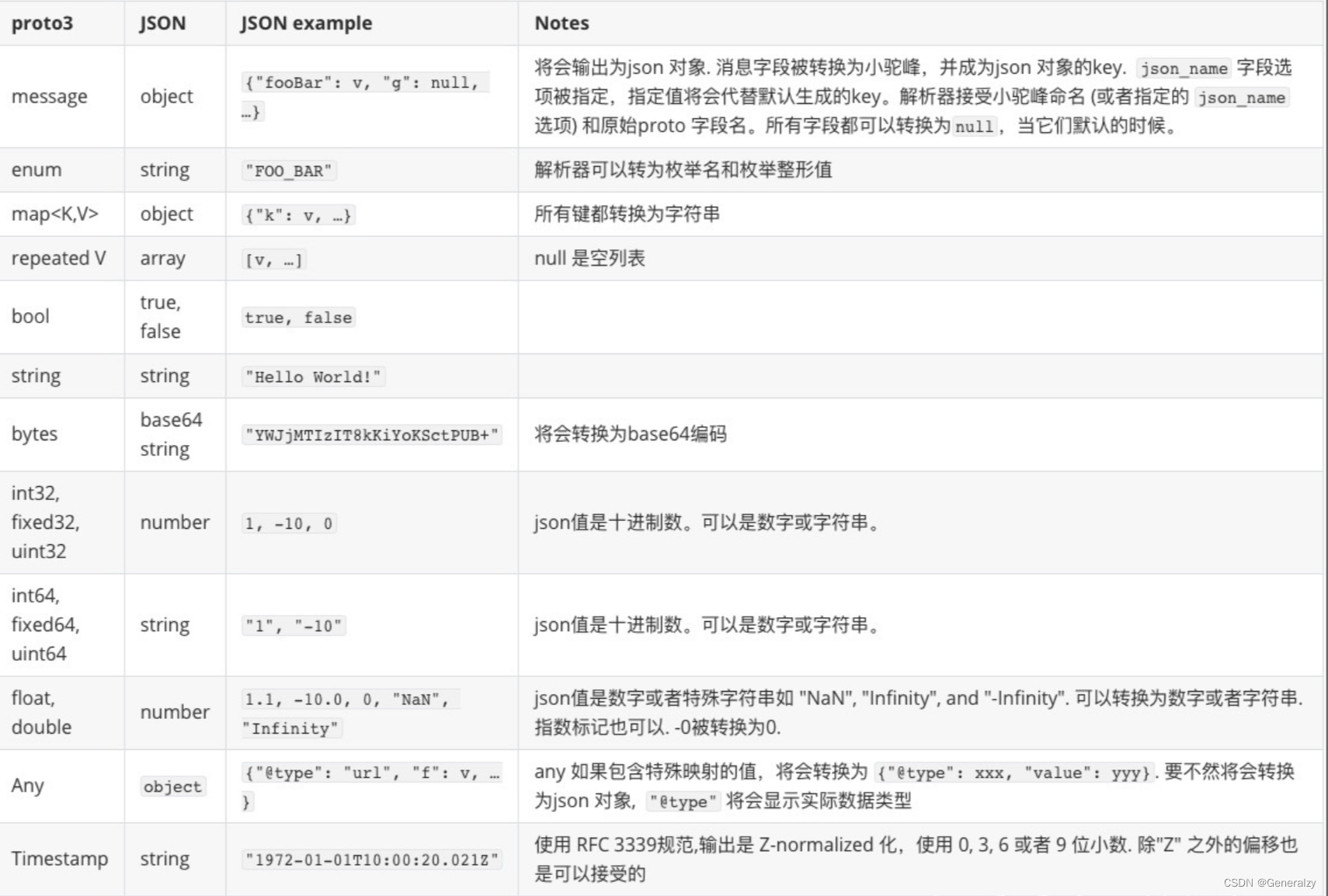
Protocol Buffers V3语法全解
目录protobuf介绍protobuf使用protoc命令语法定义消息类型指定字段类型分配字段编号指定字段规则添加更多消息类型注释保留字段从.proto文件生成了什么?值类型默认值枚举使用其他消息类型导入定义嵌套类型更新消息类型未知字段any任意类型oneofoneof 特性兼容性问题…...

MediaPipe之人体关键点检测>>>BlazePose论文精度
BlazePose: On-device Real-time Body Pose tracking BlazePose:设备上实时人体姿态跟踪 论文地址:[2006.10204] BlazePose: On-device Real-time Body Pose tracking (arxiv.org) 主要贡献: (1)提出一个新颖的身体姿态跟踪解决…...
CSS从入门到精通专栏简介
先让我们来欣赏几个精美的网站: Matt Brett - Freelance Web Designer and WordPress Expert 2022 Year in Review • Letterboxd NIO蔚来汽车官方网站 小米官网 Silk – Interactive Generative Art 大屏数据可视化 你是否也有过这样的“烦恼”: * …...

day01常用DOS命令
day01课堂笔记(第一章 Java开发环境的搭建) 1、常用的DOS命令 1.1、怎么打开DOS命令窗口 win键 r (组合键):可以打开“运行”窗口 在运行窗口文本框中输入: cmd 然后回车 1.2、什么是DOS命令呢? 在DOS命令…...
)
Java设计模式-生成器模式(建造模式)
1.1定义 维基百科定义 生成器模式(英:Builder Pattern)是一种设计模式,又名:建造模式,是一种对象构建模式。 它可以将复杂对象的建造过程抽象出来(抽象类别),使这个抽象…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
