Multi-Grade Deep Learning for Partial Differential Equations
论文阅读:Multi-Grade Deep Learning for Partial Differential Equations with Applications to the Burgers Equation
- Multi-Grade Deep Learning for Partial Differential Equations with Applications to the Burgers Equation
- 符号定义
- 偏微分方程定义
- FNN定义
- PINN定义
- 多级学习
- 两阶段模型
- 实验结果
- 1D Burgers
- 总结
Multi-Grade Deep Learning for Partial Differential Equations with Applications to the Burgers Equation
符号定义
偏微分方程定义
一个偏微分方程可以定义如下:
F ( u ( t , x ) ) = 0 , x ∈ Ω , t ∈ ( 0 , T ] , I ( u ( 0 , x ) ) = 0 , x ∈ Ω , t = 0 , B ( u ( t , x ) ) = 0 , x ∈ Γ , t ∈ ( 0 , T ] , \begin{aligned}\mathcal{F}(u(t,x))&=0,&x\in\Omega,&t\in(0,T],\\\mathcal{I}(u(0,x))&=0,&x\in\Omega,&t=0,\\\mathcal{B}(u(t,x))&=0,&x\in\Gamma,&t\in(0,T],\end{aligned} F(u(t,x))I(u(0,x))B(u(t,x))=0,=0,=0,x∈Ω,x∈Ω,x∈Γ,t∈(0,T],t=0,t∈(0,T],
其中 Ω ⊂ R d \Omega\subset\mathbb{R}^d Ω⊂Rd , d d d 为计算域的维度, Γ \varGamma Γ 为 Ω \Omega Ω 的边界,$ \mathcal{F}$ 为非线性微分算子, I , B \mathcal{I},\mathcal{B} I,B 分别表示初始条件和边界条件的(非线性)算子, u u u 是要学习的未知解。并且其中 T > 0 T > 0 T>0,初始状态 u ( 0 , x ) u(0, x) u(0,x) 和 u u u 在 Γ \varGamma Γ 上的数据已知。
FNN定义
令 s , t s,t s,t 为两个正整数。 FNN 是将 s s s 维度的输入向量映射到 t t t 维度的输出向量的函数。深度为 D D D 的 FNN 是由输入层、 D − 1 D − 1 D−1 个隐藏层和输出层组成的神经网络。令 d i d_i di 表示第 i i i 个隐藏层中的神经元数量,令 W i ∈ R d i × d i − 1 W_i\in\mathbb{R}^{d_i\times d_{i-1}} Wi∈Rdi×di−1 和 b i ∈ R d i b_i \in \mathbb{R}^{d_i} bi∈Rdi 分别表示第 i i i 层的权重矩阵和偏置向量。设 σ : R → R \sigma:\mathbb{R}\to\mathbb{R} σ:R→R 表示激活函数, x : = [ x 1 , x 2 , … , x s ] T ∈ R s \mathbf{x}:=\left.[x_1,x_2,\ldots,x_s]^T\right.\in\mathbb{R}^s x:=[x1,x2,…,xs]T∈Rs 是输入向量。第一个隐藏层的输出表示为 H 1 ( x ) \mathcal{H}_1(\mathbf{x}) H1(x),通过使用 W 1 W_1 W1 和 b 1 b_1 b1 将激活函数应用于输入的仿射变换来定义。具体来说,我们有
H 1 ( x ) = σ ( W 1 x + b 1 ) , x ∈ R s \mathcal{H}_1(\mathbf{x})=\sigma(W_1\mathbf{x}+b_1),\quad\mathbf{x}\in\mathbb{R}^s H1(x)=σ(W1x+b1),x∈Rs
其中 W 1 ∈ R d 1 × s W_1\in\mathbb{R}^{d_1\times s} W1∈Rd1×s, b 1 ∈ R d 1 b_1 \in \mathbb{R}^{d_1} b1∈Rd1 。对于深度 D ≥ 3 D \ge 3 D≥3 的神经网络,第 ( i + 1 ) (i+1) (i+1) 个隐藏层的输出可以被识别为第 i i i 个隐藏层输出的递归函数,定义为
H i + 1 ( x ) : = σ ( W i + 1 H i ( x ) + b i + 1 ) , i = 1 , 2 , … , D − 2 \mathcal{H}_{i+1}(\mathrm{x}):=\sigma(W_{i+1}\mathcal{H}_i(\mathrm{x})+b_{i+1}),\quad i=1,2,\ldots,D-2 Hi+1(x):=σ(Wi+1Hi(x)+bi+1),i=1,2,…,D−2
最后,深度为 D 的神经网络的输出定义为
N D ( x ) : = W D H D − 1 ( x ) + b D \mathcal{N}_D(\mathbf{x}):=W_D\mathcal{H}_{D-1}(\mathbf{x})+b_D ND(x):=WDHD−1(x)+bD
可训练网络参数集表示为 Θ : = { W i , b i } i = 1 D \Theta:=\{W_i,b_i\}_{i=1}^D Θ:={Wi,bi}i=1D,它由所有层的所有权重矩阵和偏差向量组成。
PINN定义
PINN 的损失函数由三个部分组成:PDE 损失、初始条件损失和边界条件损失。假设 N D \mathcal N_D ND 是一个要学习的深度神经网络,PINN的损失函数的三个分量定义如下:
-
PDE 的损失:
L o s s P D E ( N D ) : = 1 N f ∑ i = 1 N f ∣ F ( N D ( t f i , x f i ) ) ∣ 2 , ( t f i , x f i ) ∈ ( 0 , T ] × Ω , Loss_{PDE}(\mathcal{N}_D):=\frac1{N_f}\sum_{i=1}^{N_f}|\mathcal{F}(\mathcal{N}_D(t_f^i,x_f^i))|^2,\quad(t_f^i,x_f^i)\in(0,T]\times\Omega, LossPDE(ND):=Nf1i=1∑Nf∣F(ND(tfi,xfi))∣2,(tfi,xfi)∈(0,T]×Ω,其中, ( t f i , x f i ) (t_f^i,x_f^i) (tfi,xfi) 是从计算域中随机生成的采样点。
-
初始条件损失:
L o s s I ( N D ) : = 1 N 0 ∑ i = 1 N 0 ∣ L ( N D ( 0 , x 0 i ) ) ∣ 2 , x 0 i ∈ Ω Loss_I(\mathcal{N}_D):=\frac1{N_0}\sum_{i=1}^{N_0}|\mathcal{L}(\mathcal{N}_D(0,x_0^i))|^2,\quad x_0^i\in\Omega LossI(ND):=N01i=1∑N0∣L(ND(0,x0i))∣2,x0i∈Ω
其中, x 0 i x_0^i x0i 是在初始条件上随机生成的采样点。 -
边界条件损失:
L o s s B ( N D ) : = 1 N b ∑ i = 1 N b ∣ B ( N D ( t b i , x b i ) ) ∣ 2 , ( t b i , x b i ) ∈ ( 0 , T ] × Γ Loss_B(\mathcal{N}_D):=\frac1{N_b}\sum_{i=1}^{N_b}\left|\mathcal{B}(\mathcal{N}_D(t_b^i,x_b^i))\right|^2,\quad(t_b^i,x_b^i)\in(0,T]\times\Gamma LossB(ND):=Nb1i=1∑Nb B(ND(tbi,xbi)) 2,(tbi,xbi)∈(0,T]×Γ
其中, ( t b i , x b i ) (t_b^i,x_b^i) (tbi,xbi) 是从边界上随机生成的采样点。
于是,总的PINN损失如下:
L o s s ( N D ) : = L o s s P D E ( N D ) + L o s s I ( N D ) + L o s s B ( N D ) . Loss(\mathcal{N}_D):=Loss_{PDE}(\mathcal{N}_D)+Loss_I(\mathcal{N}_D)+Loss_B(\mathcal{N}_D). Loss(ND):=LossPDE(ND)+LossI(ND)+LossB(ND).
PINN 的主要思想是利用神经网络通过最小化损失函数(残差)来学习 PDE 的近似解。令 N D ( ∙ ) : = N D ( Θ ; ∙ ) \mathcal{N}_D(\bullet):= \mathcal{N}_D(\Theta;\bullet) ND(∙):=ND(Θ;∙) 为具有深度 D D D 和网络参数 Θ \Theta Θ 的神经网络。为了获得PDE的近似解,PINN相对于网络参数 Θ \Theta Θ 最小化上式定义的损失函数,即
min Θ L o s s ( N D ( Θ ; ∙ ) ) \min_\Theta Loss(\mathcal{N}_D(\Theta;\bullet)) ΘminLoss(ND(Θ;∙))
多级学习
可以通过定义一个深度为 k 1 k_1 k1 的神经网络 N k 1 \mathcal N_{k_1} Nk1 开始,其参数为 Θ 1 : = { W i 1 , b i 1 } i = 1 k 1 \Theta_1:=\{W^1_i,b^1_i\}_{i=1}^{k_1} Θ1:={Wi1,bi1}i=1k1。于是可以设置 u 1 = u 1 ( Θ 1 ; ∙ ) : = N k 1 ( Θ 1 ; ∙ ) u_1=u_1(\Theta_1;\bullet):=\mathcal{N}_{k_1}(\Theta_1;\bullet) u1=u1(Θ1;∙):=Nk1(Θ1;∙) 为 1 级神经网络。为了学习 1 级参数,可以对如下最小化问题求解:
min Θ 1 L o s s ( u 1 ( Θ 1 ; ∙ ) ) \min_{\Theta_1}Loss(u_1(\Theta_1;\bullet)) Θ1minLoss(u1(Θ1;∙))
对上述最小化问题求解后,就得到了 1 级的近似解,表示为 u 1 ∗ = N k 1 ∗ : = N k 1 ( Θ 1 ∗ ; ∙ ) u_1^*=\mathcal{N}_{k_1}^*:=\mathcal{N}_{k_1}(\Theta_1^*;\bullet) u1∗=Nk1∗:=Nk1(Θ1∗;∙),其中 Θ 1 ∗ : = { W i 1 ∗ , b i 1 ∗ } i = 1 k 1 \Theta_1^*:=\{W_i^{1*},b_i^{1*}\}_{i=1}^{k_1} Θ1∗:={Wi1∗,bi1∗}i=1k1 是学习到的参数。于是近似解 u 1 u_1 u1 可以表示为:
u 1 ∗ ( x ) = W k 1 1 ∗ H k 1 − 1 1 ∗ ( x ) + b k 1 1 ∗ u_1^*(\mathbf{x})=W_{k_1}^{1*}\mathcal{H}_{k_1-1}^{1*}(\mathbf{x})+b_{k_1}^{1*} u1∗(x)=Wk11∗Hk1−11∗(x)+bk11∗
其中 H k 1 − 1 1 ∗ \mathcal{H}_{k_1-1}^{1*} Hk1−11∗ 是没有输出层的网络 N k 1 1 ∗ \mathcal{N}_{k_1}^{1*} Nk11∗, W k 1 1 ∗ W_{k_1}^{1*} Wk11∗ 表示连接最后一个隐藏层和输出层的权重矩阵, b k 1 1 ∗ b_{k_1}^{1*} bk11∗ 表示相应的偏差向量。
接下来,就可以构建 2 级神经网络,用 u 2 u_2 u2 表示,它建立在 1 级神经网络之上,使用网络 N k 2 : = N k 2 ( Θ 2 ; ∙ ) \mathcal{N}_{k_2}:=\mathcal{N}_{k_2}(\Theta_2;\bullet) Nk2:=Nk2(Θ2;∙) ,参数 Θ 2 : = { W j 2 , b j 2 } j = 1 k 2 \Theta_2:=\{W^2_j,b^2_j\}_{j=1}^{k_2} Θ2:={Wj2,bj2}j=1k2。具体来说,就是首先删除 1 级的输出层,并将网络 N k 2 \mathcal{N}_{k_2} Nk2 堆叠在 1 级的最后一个隐藏层之上,以定义 2 级的神经网络。即,
u 2 = u 2 ( Θ 1 ; ∙ ) : = N k 2 ( Θ 2 ; ∙ ) ∘ H k 1 − 1 1 ∗ u_2=u_2(\Theta_1;\bullet):=\mathcal{N}_{k_2}(\Theta_2;\bullet)\circ\mathcal{H}_{k_1-1}^{1*} u2=u2(Θ1;∙):=Nk2(Θ2;∙)∘Hk1−11∗
其中“ ∘ \circ ∘”表示复合算子, H k 1 − 1 1 ∗ \mathcal{H}_{k_1-1}^{1*} Hk1−11∗ 是没有输出层的网络 N k 1 1 ∗ \mathcal{N}_{k_1}^{1*} Nk11∗。

2级神经网络的参数可以通过解决如下最小化问题来进行学习:
min Θ 2 L o s s ( u 1 ∗ ( ∙ ) + u 2 ( Θ 2 ; ∙ ) ) \min_{\Theta_2}Loss(u_1^*(\bullet)+u_2(\Theta_2;\bullet)) Θ2minLoss(u1∗(∙)+u2(Θ2;∙))
得到最优参数 Θ 2 ∗ : = { W j 2 ∗ , b j 2 ∗ } j = 1 k 2 \Theta_2^*:=\{W_j^{2*},b_j^{2*}\}_{j=1}^{k_2} Θ2∗:={Wj2∗,bj2∗}j=1k2 并定义:
u 2 ∗ : = u 2 ( Θ 2 ∗ ; ∙ ) = N k 2 ( Θ 2 ∗ ; ∙ ) ∘ H k 1 − 1 1 ∗ u_2^*:=u_2(\Theta_2^*;\bullet)=\mathcal{N}_{k_2}(\Theta_2^*;\bullet)\circ\mathcal{H}_{k_1-1}^{1*} u2∗:=u2(Θ2∗;∙)=Nk2(Θ2∗;∙)∘Hk1−11∗
值得注意的是, H k 1 − 1 1 ∗ \mathcal{H}_{k_1-1}^{1*} Hk1−11∗ 在训练过程中是固定的,于是从上式中可以看出, u 2 ∗ u_2^* u2∗ 学习了 1 级解 u 1 ∗ u_1^* u1∗ 的残差,以更好地逼近偏微分方程的解。
于是可以通过重复上述过程来构造一个 ℓ + 1 \ell+1 ℓ+1 级的神经网络。假设对于 1 ≤ i ≤ ℓ 1 \le i \le \ell 1≤i≤ℓ,已经学习了 i i i 级的神经网络 u i u_i ui,可以使用参数为 Θ ℓ + 1 : = { W j ℓ + 1 , b j ℓ + 1 } j = 1 k ℓ + 1 \Theta_{\ell+1}:=\{W_j^{\ell+1},b_j^{\ell+1}\}_{j=1}^{k_{\ell+1}} Θℓ+1:={Wjℓ+1,bjℓ+1}j=1kℓ+1 的神经网络 N k ℓ + 1 ( Θ ℓ + 1 ; ∙ ) \mathcal{N}_{k_{\ell+1}}(\Theta_{\ell+1};\bullet) Nkℓ+1(Θℓ+1;∙) 定义 ℓ + 1 \ell+1 ℓ+1级神经网络 u ℓ + 1 u_{\ell+1} uℓ+1,即
u ℓ + 1 ( Θ ℓ + 1 ; x ) : = ( N k ℓ + 1 ( Θ ℓ + 1 ; ∙ ) ∘ H k ℓ − 1 ℓ ∗ ∘ ⋯ ∘ H k 2 − 1 2 ∗ ∘ H k 1 − 1 1 ∗ ) ( x ) u_{\ell+1}(\Theta_{\ell+1};\mathbf{x}):=(\mathcal{N}_{k_{\ell+1}}(\Theta_{\ell+1};\bullet)\circ\mathcal{H}_{k_{\ell}-1}^{\ell*}\circ\cdots\circ\mathcal{H}_{k_2-1}^{2*}\circ\mathcal{H}_{k_1-1}^{1*})(\mathbf{x}) uℓ+1(Θℓ+1;x):=(Nkℓ+1(Θℓ+1;∙)∘Hkℓ−1ℓ∗∘⋯∘Hk2−12∗∘Hk1−11∗)(x)
其中 H k i − 1 i ∗ \mathcal{H}_{k_i-1}^{i*} Hki−1i∗ 表示没有输出层的神经网络 N k i ∗ : = N k i ( Θ i ∗ ; ∙ ) \mathcal{N}_{k_i}^*:=\mathcal{N}_{k_i}(\Theta_i^*;\bullet) Nki∗:=Nki(Θi∗;∙),学习参数为 { W j i ∗ , b j i ∗ } j = 1 k i − 1 , i = 1 , 2 , … , ℓ . \{W_j^{\boldsymbol{i}*},b_j^{\boldsymbol{i}*}\}_{j=1}^{\boldsymbol{k}_i-1},i=1,2,\ldots,\ell. {Wji∗,bji∗}j=1ki−1,i=1,2,…,ℓ. 通过求解如下最小化问题可以得到 ℓ + 1 \ell+1 ℓ+1 级最优参数 Θ ℓ + 1 ∗ = { W j ℓ + 1 ∗ , b j ℓ + 1 ∗ } j = 1 k ℓ + 1 \Theta_{\ell+1}^*=\left.\{W_j^{\ell+1*},b_j^{\ell+1*}\}_{j=1}^{k_{\ell+1}}\right. Θℓ+1∗={Wjℓ+1∗,bjℓ+1∗}j=1kℓ+1
min Θ ℓ + 1 L o s s ( ∑ i = 1 ℓ u i ∗ ( ∙ ) + u ℓ + 1 ( Θ ℓ + 1 ; ∙ ) ) \min_{\Theta_{\ell+1}}Loss\left(\sum_{i=1}^{\ell}u_i^*(\bullet)+u_{\ell+1}(\Theta_{\ell+1};\bullet)\right) Θℓ+1minLoss(i=1∑ℓui∗(∙)+uℓ+1(Θℓ+1;∙))
然后可以令 u ℓ + 1 ∗ : = u ℓ + 1 ( Θ ℓ + 1 ∗ ; ∙ ) u_{\ell+1}^*:=u_{\ell+1}(\Theta_{\ell+1}^*;\bullet) uℓ+1∗:=uℓ+1(Θℓ+1∗;∙)。最后,通过对所有 ℓ + 1 \ell + 1 ℓ+1 个等级的近似值求和,可以得到神经网络
u ˉ ℓ + 1 ∗ : = ∑ i = 1 ℓ + 1 u i ∗ \bar{u}_{\ell+1}^*:=\sum_{i=1}^{\ell+1}u_i^* uˉℓ+1∗:=i=1∑ℓ+1ui∗
两阶段模型
前文中描述的学习策略涉及逐级学习的方法。随着级数的增加,需要学习的残差振荡变得更加明显。然而,由于每个等级的神经网络的层数相对较少(在稍后介绍的实验中通常少于 6 层),网络可能难以捕获底层残差振荡中包含的更复杂的模式。此外,MGDL 模型可能会陷入局部最小化器而错过全局最小化器。解决这些问题需要扩大优化器的搜索区域。为此,作者解冻了先前级和以前的一些训练过的网络的一些层并对它们进行重新训练,以提高生成的 DNN 解决方案的准确性。这个过程被称为训练的第二阶段。
下面描述第二阶段的训练。假设经过第一阶段的训练,已经构建了神经网络 u ˉ L ∗ : = ∑ i = 1 L u i ∗ \bar{u}_L^*:=\sum_{i=1}^Lu_i^* uˉL∗:=∑i=1Lui∗,其具有 L L L 级。其近似解 u L ∗ u^*_L uL∗ 具有如下表达式:
u L ∗ ( x ) : = ( N k L ∗ ∘ H k L − 1 L − 1 ∗ ∘ ⋯ ∘ H k 2 − 1 2 ∗ ∘ H k 1 − 1 1 ∗ ) ( x ) u_L^*(\mathbf{x}):=(\mathcal{N}_{k_L}^*\circ\mathcal{H}_{k_L-1}^{L-1*}\circ\cdots\circ\mathcal{H}_{k_2-1}^{2*}\circ\mathcal{H}_{k_1-1}^{1*})(\mathbf{x}) uL∗(x):=(NkL∗∘HkL−1L−1∗∘⋯∘Hk2−12∗∘Hk1−11∗)(x)
其中 N k L ∗ \mathcal{N}^*_{k_L} NkL∗ 在 L L L 级进行训练,其参数为 Θ L ∗ \Theta^*_L ΘL∗。可以解冻 u L ∗ u^*_L uL∗ 的最后 k k k 层作为新的可训练层,其中 k > k L k \gt k_L k>kL。可以表示为:
Θ L , k : = { W j L , k , b j L , k } j = 1 k \Theta_{L,k}:=\{W_j^{L,k},b_j^{L,k}\}_{j=1}^k ΘL,k:={WjL,k,bjL,k}j=1k
可以使用符号 u ~ L : = u ~ L ( Θ L , k ; ∙ ) \widetilde{u}_L:=\widetilde{u}_L(\Theta_{L,k};\bullet) u L:=u L(ΘL,k;∙) 来表示通过解冻 u L ∗ u^*_L uL∗ 最后 k k k 层并解决最小化问题而从 u L ∗ u^*_L uL∗ 获得的神经网络
min Θ L , k L o s s ( u ˉ L − 1 ∗ ( ∙ ) + u ~ L ( Θ L , k ; ∙ ) ) . \min_{\Theta_{L,k}}Loss(\bar{u}_{L-1}^*(\bullet)+\widetilde{u}_L(\Theta_{L,k};\bullet)). ΘL,kminLoss(uˉL−1∗(∙)+u L(ΘL,k;∙)).
可以使用 u L ∗ u^*_L uL∗ 的 k k k 层参数作为初始化来解决上述最小化问题,并获得新参数 Θ L , k ∗ \Theta^*_{L,k} ΘL,k∗。然后可以定义函数 u ~ L ∗ : = u ~ L ( Θ L , k ∗ ; ∙ ) \widetilde{u}_L^*:=\widetilde{u}_L(\Theta_{L,k}^*;\bullet) u L∗:=u L(ΘL,k∗;∙)。因此,第二阶段生成 PDE 的近似解,由下式给出
u a p p r : = u ˉ L − 1 ∗ + u ~ L ∗ u_{appr}:=\bar{u}_{L-1}^*+\widetilde{u}_L^* uappr:=uˉL−1∗+u L∗

实验结果
作者将提出的 TS-MGDL 方法应用于 1D、2D 和 3D Burgers 方程的求解上并与单级方法进行了对比。
1D Burgers
u t ( t , x ) + u ( t , x ) u x ( t , x ) − 0.01 π u x x ( t , x ) = 0 , t ∈ ( 0 , 1 ] , x ∈ ( − 1 , 1 ) , u_t(t,x)+u(t,x)u_x(t,x)-\frac{0.01}\pi u_{xx}(t,x)=0,\quad t\in(0,1],x\in(-1,1), ut(t,x)+u(t,x)ux(t,x)−π0.01uxx(t,x)=0,t∈(0,1],x∈(−1,1),
初始条件与边界条件如下:
u ( 0 , x ) = − sin ( π x ) , u ( t , − 1 ) = u ( t , 1 ) = 0 u(0,x)=-\sin(\pi x),\\ u(t,-1)=u(t,1)=0 u(0,x)=−sin(πx),u(t,−1)=u(t,1)=0
作者采用哈默斯利采样方法随机生成训练样本点。沿着边界,总共生成了 N b : = 80 N_b := 80 Nb:=80 个随机点。此外,根据初始条件生成 N 0 : = 120 N_0 := 120 N0:=120 个随机点。在内部区域 ( 0 , 1 ] × ( − 1 , 1 ) (0, 1] × (−1, 1) (0,1]×(−1,1) 中,生成 N f : = 10 , 000 N_f := 10, 000 Nf:=10,000 个随机点。测试集由时空区域 [ 0 , 1 ] × [ − 1 , 1 ] [0, 1] × [−1, 1] [0,1]×[−1,1] 均匀划分得到的网格点组成,测试点总数为 100 × 256 100×256 100×256。

上表为作为对比的三个单级方法的神经网络设置

上表为对应的多级网络的设置,这里一共有三级。数字旁边的星号(*)表示第一阶段本级训练时,对应的权重参数固定为前年级训练的权重参数。

上表为多级网络的训练结果,可以看到,作者在不同级数设置了不同的学习率和epoch。
为早期等级设置更高的学习率,可以使网络快速学习基本(大规模)特征,并继续学习更复杂(小规模)特征。这可以加快训练过程并提高网络的整体准确性。而在更高等级使用较低的学习率有助于微调学习的表示并提高网络的准确性。在训练的第二阶段,使用低学习率使网络能够仔细调整这些表示以更好地适应训练数据,从而提高准确性。
同样,如果早期级数中的epoch数量太大,则可能会陷入不需要的局部最小值,这可能会导致后续等级的优化变得困难。在第一阶段的训练过程中,随着级数的提高,训练难度逐渐加大,epoch数也要相应增加。由于梯度下降通常在迭代开始时表现出损失更快的下降,因此可以通过在第一阶段为等级设置较少量的epoch来利用这一点来捕捉快速下降的阶段。另一方面,在第二阶段建议使用更多的epoch以实现增强的数值近似。

上表为多级网络和三个单级网络的对比。

上图为不同阶段结果的可视化。

误差的可视化。

上图为四个方法训练时的loss下降情况。
总结
本文针对PDE求解问题,通过设计多级神经网络结构,来让后续网络层学习先前网络层的误差,并设计了对应的两阶段训练方式。最后通过数值实验验证了其有效性。
可以看出来,作者是想模仿Res-Net的方法,但似乎只是更改网络结构带来的数值精度提高并不明显,所以又设计了二阶段训练方式。感觉可以增加对单级神经网络使用二阶段训练的实验作为对比,那样或许会更有说服力。目前本文还未公开代码,但文中说是用DeepXDE实现的。等他公开代码了我应该会来试一下,但感觉我对网络结构方面的研究没太大兴趣呢。
相关链接:
- 原文:[2309.07401] Multi-Grade Deep Learning for Partial Differential Equations with Applications to the Burgers Equation (arxiv.org)
相关文章:

Multi-Grade Deep Learning for Partial Differential Equations
论文阅读:Multi-Grade Deep Learning for Partial Differential Equations with Applications to the Burgers Equation Multi-Grade Deep Learning for Partial Differential Equations with Applications to the Burgers Equation符号定义偏微分方程定义FNN定义PI…...

Docker部署rustdesk
查看镜像版本 https://hub.docker.com/r/rustdesk/rustdesk-server/tags 拉取镜像 docker pull rustdesk/rustdesk-server:1.1.8-2创建挂载目录 mkdir -p /opt/rustdesk/{hbbr,hbbs}/root运行hbbs –nethost 仅适用于 Linux,它让 hbbs/hbbr 可以看到对方真实的…...

win1011安装MG-SOFT+MIB+Browser+v10b
文章目录 安装MG-SOFTSNMP服务配置安装MG-SOFT启动MIB-Browser以及错误解决MIB Browser使用 安装MG-SOFT win10和win11安装基本一样,所以参照下面的操作即可! SNMP服务配置 打开设置,应用和功能,可选功能,选择添加功…...
)
PCL点云处理之Pcd文件读取、法线与曲率计算、多线程加速、属性字段合并 (二百零八)
PCL点云处理之Pcd文件读取、法线与曲率计算、多线程加速、属性字段合并(二百零八) 一、相关介绍二、算法实现1.代码一、相关介绍 (夜深人不静) 法线和曲率的计算是点云处理中常用的关键特征,PCL提供了特有的点类型PointNormal来记录这些信息,通过OMP多线程对相关的计算函…...
JavaEE-文件IO操作
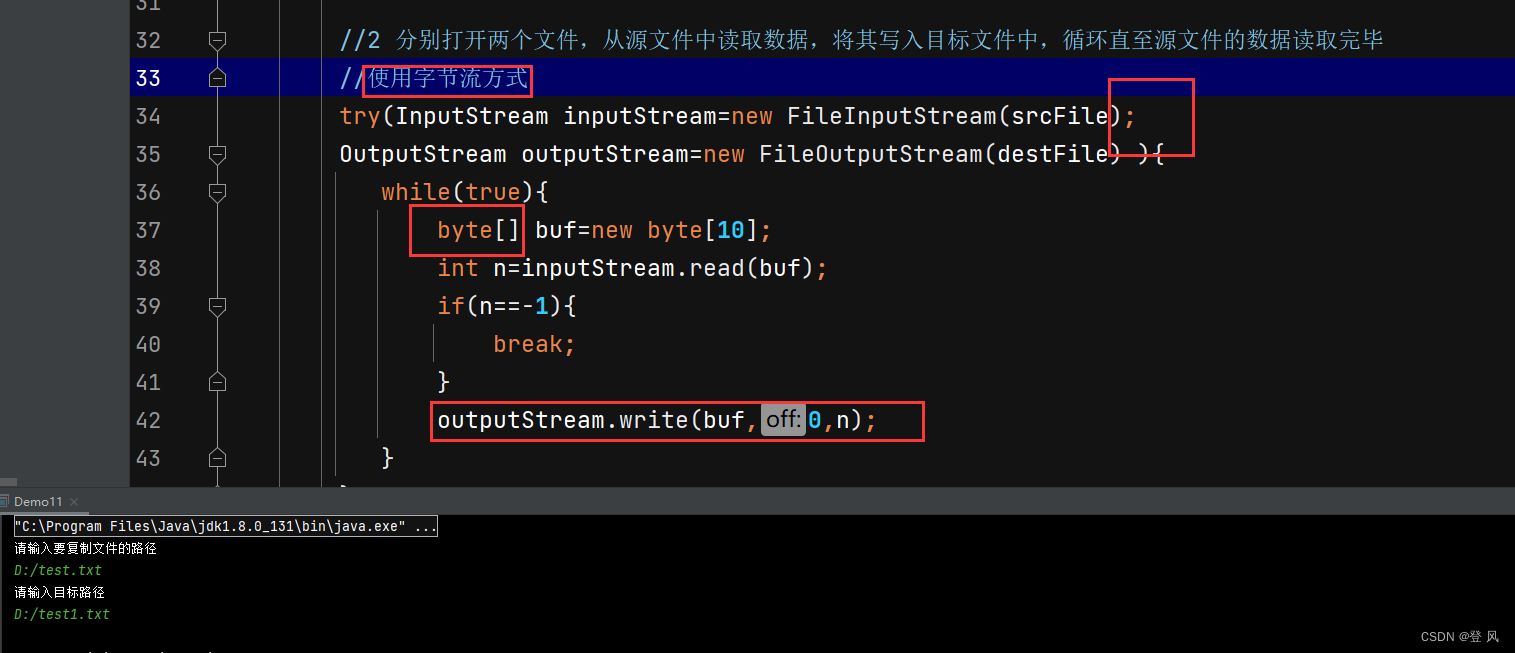
构造方法 一般方法,有很多,我们以下只是列举几个经常使用的 注意在上述的操作过程中,无论是绝对路径下的这个文件还是相对路径下的这个文件,都是不存在的 Reader 使用 --> 文本文件 FileReader类所涉及到的一些方法 Fil…...

二蛋赠书四期:《Go编程进阶实战:开发命令行应用、HTTP应用和gRPC应用》
前言 大家好!我是二蛋,一个热爱技术、乐于分享的工程师。在过去的几年里,我一直通过各种渠道与大家分享技术知识和经验。我深知,每一位技术人员都对自己的技能提升和职业发展有着热切的期待。因此,我非常感激大家一直…...
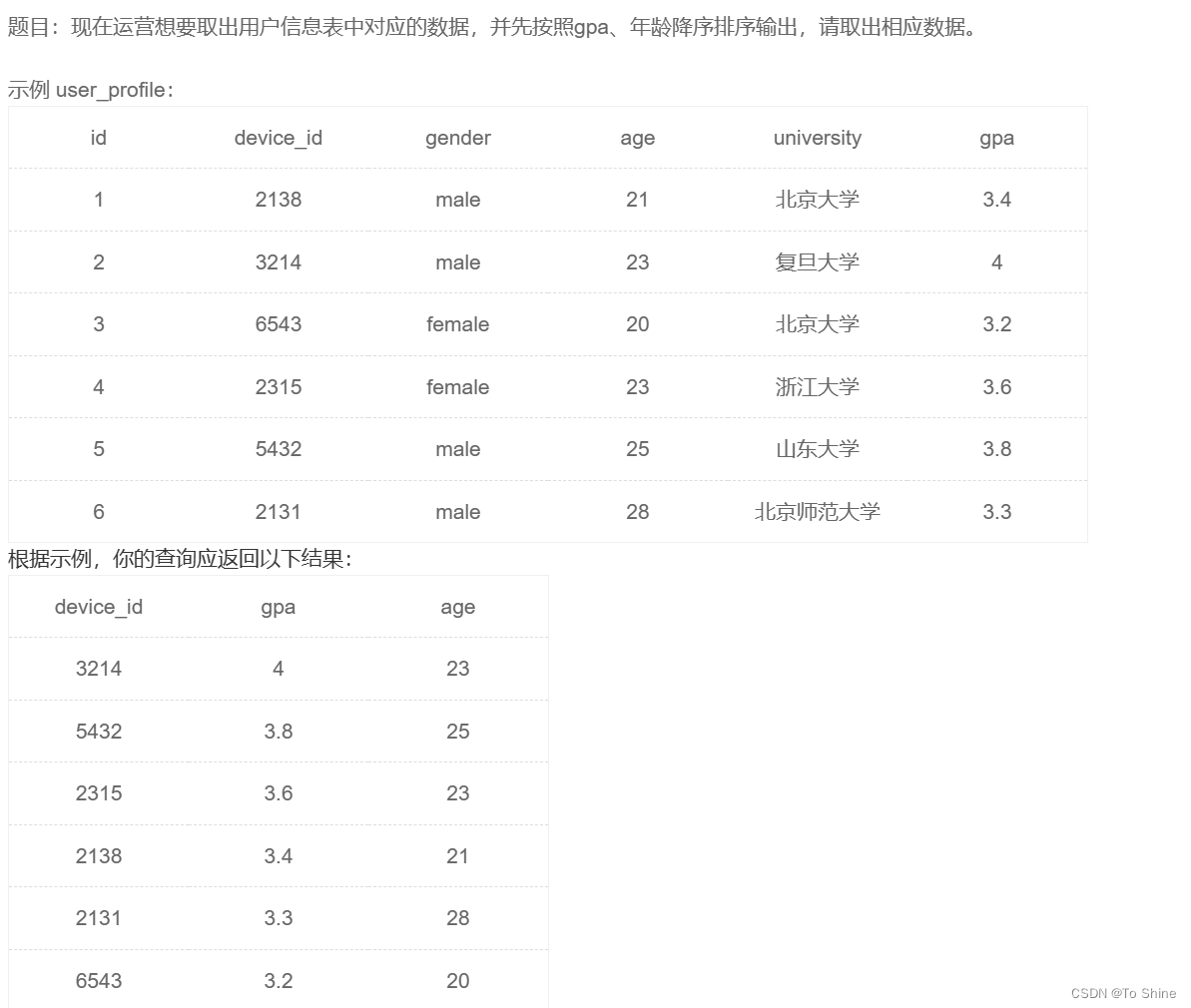
MySQL数据库基本操作-DQL-排序查询
介绍 如果我们需要对读取的数据进行排序,我们就可以使用 MySQL 的 order by 子句来设定你想按哪个字段哪种方式来进行排序,再返回搜索结果。 语法 select 字段名1,字段名2,…… from 表名 order by 字段名1 [asc|desc]…...

这是一篇测试文章
这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章这是一篇测试文章…...

Ubuntu plt画图 新罗马字体网格marker刻度朝内
* 字体文件:坚果云下code包,新罗马字体 参考链接:Linux下Matplotlib画图New Times Roman字体设置 - 知乎 * 刻度朝内 plt.rcParams[font.sans-serif] [Times New Roman]plt.rcParams[xtick.direction]in#设置x轴刻度向内plt.rcParams[ytic…...

flutter布局中的一些细节
前言 记录flutter使用中遇到的一些细节和坑,希望能帮助到大家 Column中不能直接嵌套ListView, (需要指定ListView的高度或者加上shrinkWrap: true属性)需要限制button的大小,可以在外部嵌套一个Container或SizedBox来限制在List…...
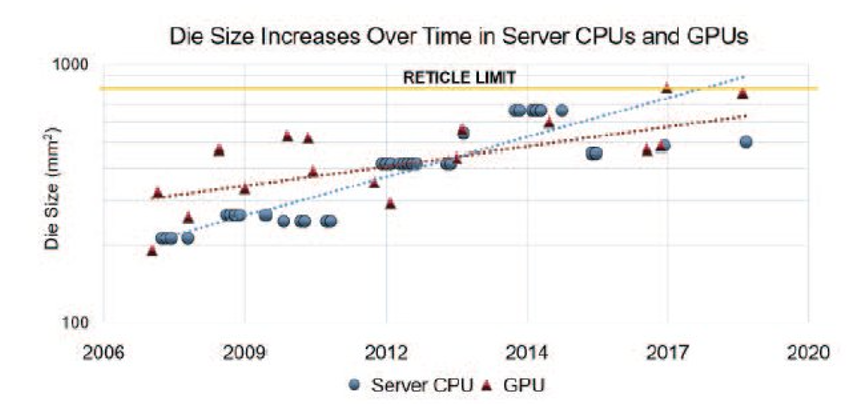
论文解析——AMD EPYC和Ryzen处理器系列的开创性的chiplet技术和设计
ISCA 2021 摘要 本文详细解释了推动AMD使用chiplet技术的挑战,产品开发的技术方案,以及如何将chiplet技术从单处理器扩展到多个产品系列。 正文 这些年在将SoC划分成多个die方面有一系列研究,MCM的概念也在不断更新,AMD吸收了…...

第二证券:汽车产业链股活跃,恒勃股份、博俊科技“20cm”涨停
轿车产业链股9日盘中走势活跃,截至发稿,恒勃股份、博俊科技“20cm”涨停,德迈仕涨超17%,上声电子涨超14%,川环科技涨超10%,圣龙股份、科华控股、沪光股份、上海沿浦、日盈电子、赛力斯等均涨停。 工作方面…...

孙帅Spring源码
【视频来源于:B站up主孙帅suns Spring源码视频】【微信号:suns45】...

jenkins工具系列 —— 插件 使用Changelog获取commit记录
文章目录 安装changelog插件重启jenkins配置 ChangelogExecute shell 使用 changelog邮件中html格式也可以使用构建测试(查看构建项 -> 控制台输出) 安装changelog插件 插件文件可通过 V 获取 点击 左侧的 Manage Jenkins —> Plugins ——> …...
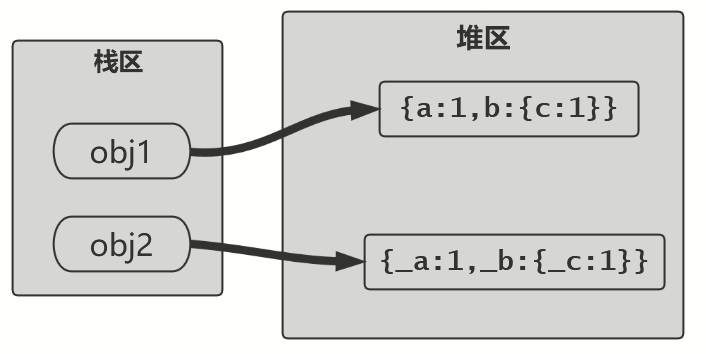
【JavaScript】浅拷贝与深拷贝
引言 浅拷贝、深拷贝是对引用类型而言的。 引用类型的变量对应一个栈区地址,这个栈区地址处存储的值是存放的真正的数据的堆区地址。 基本数据类型的变量也对应一个栈区地址,但是该地址存储的是其真正的值。 let a b发生了什么? let obj…...
如何下载IEEE Journal/Conference/Magazine的LaTeX/Word模板
当你准备撰写一篇学术论文或会议论文时,使用IEEE(电气和电子工程师协会)的LaTeX或Word模板是一种非常有效的方式,它可以帮助你确保你的文稿符合IEEE出版的要求。无论你是一名研究生生或一名资深学者,本教程将向你介绍如…...

nvidia 驱动问题
https://stackoverflow.com/questions/43022843/nvidia-nvml-driver-library-version-mismatch https://zhuanlan.zhihu.com/p/643773939...
PDF编辑和OCR文字识别工具ABBYY FineReader PDF
ABBYY FineReader PDF是一款专业的OCR文字识别和PDF编辑工具,可以帮助用户更好地处理和管理PDF文档。以下是ABBYY FineReader PDF的一些特点: 1. 文字识别精准:ABBYY FineReader PDF具有强大的OCR文字识别功能,可以将PDF中的文字…...

什么是网络流量监控
随着许多服务迁移到云,网络基础架构的维护变得复杂。虽然云采用在生产力方面是有利的,但它也可能让位于未经授权的访问,使 IT 系统容易受到安全攻击。 为了确保其网络的安全性和平稳的性能,IT 管理员需要监控用户访问的每个链接以…...

ubuntu 终端 中文显示unicode码、乱码
Ubuntu默认的中文字符编码 locale命令查看 LANG 等参数是否无UTF-8等参数?比如 为空? Ubuntu默认的中文字符编码为zh_CN.UTF-8,这个可以在 /etc/environment中看到: sudo gedit /etc/environment 可以看到如下内容: P…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
