arc 166 a
#include<bits/stdc++.h>
using namespace std;
using VI = vector<int>;
using ll = long long;
const int mod = 998244353;
//当只有ab的时候,看作把a可以向右移动
//1 - x 是a 1 - y a
//x中的 a 的 下标 <= y 中 a 的下标
//这样就可以通过位移得到
// c - c 这种情况是不可能进行移动的,所以就考虑在 c - c 将x y 分界
//考虑如何变 a , b 首先数量都是对的 , 然后将a尽量放在左边
void solve(){int n;cin>>n;string x,y;cin>>x>>y;bool ok = true;for(int i = 0 ; i < n ; i++){if(x[i] != 'C' && y[i] == 'C'){ok = false;}}x += 'C';y += 'C';int amax = 0 ;//把所有的c变成a的数量int amin = 0 ;//纯a的数量for(int i = 0 ; i <= n ; i++){if(x[i] == 'A'){amax ++;amin ++;}else if(x[i] == 'C'){amax++;}if(y[i] == 'C'){if(amin > 0)ok = false;amax = 0 ;amin = 0 ;}else if(y[i] == 'B'){}else if(y[i] == 'A'){amax--;amin--;amin = max(amin , 0);if(amax < 0) ok = false;}//if(amax < amin) ok = false;}if(ok)cout<<"Yes\n";else cout<<"No\n";}int main(){int t;cin>>t;while(t--){solve();}}首先将考虑只有ab的时候,可以发现a是可以不断向右移动的
可以证明只有当 X中a的数量 = y中a的数量 且对于 Xk <= Yk (X中第k个A的下标 小于等于 Y的第k个A下标)
对于存在C
X[i] = Y[i] = C 时的点是不能动的 , 以次为边界,将字符串进行分割,每一段都要分别满足
考虑每一段该如何构造,考虑两种情况是不满足的
1. a太多了 , 即使c不变a也分不掉,
BAAACAB
BAAABBB
这种情况用amin代表有多少个A没被分配到 ,不断统计X中a的数量 , Y中出现就 -1
当分界时候 如果还有a没被分掉,就代表false
2.a+c 太少了,在某一个点就不够分 ,
BABBBCB
BBAAABA
amax统计a + c 的数量, 如果Y中出现 a 就 - 1 ,
如果变成负数,就代表不够分
相关文章:

arc 166 a
#include<bits/stdc.h> using namespace std; using VI vector<int>; using ll long long; const int mod 998244353; //当只有ab的时候,看作把a可以向右移动 //1 - x 是a 1 - y a //x中的 a 的 下标 < y 中 a 的下标 //这样就可以通过位移得到 …...

Lua05——Lua基本数据类型
lua 是动态类型语言,变量使用前不需要定义类型,在使用时直接赋值即可。 1 基本数据类型 值可以存储在变量中,作为参数传递或作为结果返回。 lua中有八个基本数据类型: nil 只有值nil属于该类,表示一个无效值&#…...
一文3000字从0到1使用pytest-xdist实现分布式APP自动化测试
目录 01、分布式测试的原理 02、测试项目 03、环境准备 04、搭建步骤 05、分布式执行 06、测试报告 不知道大家有没有遇到这样一种情况,实际工作中,app自动化测试的用例可能是成百上千条的,如果放在一台机器上跑,消耗的时间…...

pyqt5:pandas 读取 Excel文件或 .etx 电子表格文件,并显示
pip install pandas ; pip install pyqt5; pip install pyqt5-tools; 编写 pyqt5_read_etx.py 如下 # -*- coding: utf-8 -*- """ pandas 读取 Excel文件或 .etx 电子表格文件,显示在 QTableWidget 中 """ import os import sys…...

【QT】Windows 编译并使用 QT 5.12.7源码
1、下载 QT 源码 QT5.12.7源码下载地址: download | QT 5.12.7 选择任意一种下载即可,适用于 Windows 和 Linux 环境 这里选择下载 .zip 文件。 2、安装依赖 (1) 安装 perl perl 安装包下载地址: download | perl for windows 根据当前系统选择对应版本。…...
获取GET和POST请求参数)
php实战案例记录(15)获取GET和POST请求参数
在PHP中,可以使用$_GET和$_POST超全局变量来获取GET和POST请求参数。 获取GET请求参数: 要获取GET请求参数,可以使用$_GET超全局变量。它是一个关联数组,其中键是参数的名称,值是参数的值。例如,如果URL是…...
k8s-9 ingress-nginx 特性
TLS加密 创建证书 测试 auth认证 创建认证文件 rewrite重定向 进入域名 会自动重定向hostname.html 示例二: 测试 后面必须跟westos 这个关键字 canary金丝雀发布 基于header灰度 场景:版本的升级迭代,比如一个service 升级到另…...

java案例24:模拟百度翻译
思路: 编写一个程序模拟百度翻译 用户输入英文之后,搜索程序中对应的中文, 如果搜索到1对应的中文,就输出搜索结果,反之给出提示 要求使用Map集合实现英文与中文的存储。1.百度翻译主要用于翻译对应的意思,…...

汽车烟雾测漏仪(EP120)
【汽车烟雾测漏仪(EP120)】 此烟雾测漏仪专为车辆管道(油道、气道、冷却管道) 的泄露检测而设计。适用于所有轻型 汽车、摩托车、轻卡、游艇等。 【特点】 具有空气模式和烟雾模式。空气模式,无需烟雾,检测…...

【轻松玩转MacOS】安全隐私篇
引言 这一篇将介绍如何保护MacOS的安全,包括如何设置密码,使用防火墙,备份数据等重要环节,避免因不慎操作或恶意攻击带来的安全风险,让你的MacOS之旅更安心、更放心。 一、设置密码:保护你的MacOS的第一道…...
4.02 用户中心-上传头像功能开发
详细内容请看下面地址: 地址:http://www.gxcode.top/code...

在Ubuntu 18.04安装Docker
安装需要的包 $ sudo apt-get update 安装 apt 依赖包,用于通过HTTPS来获取仓库 $ sudo apt-get install \apt-transport-https \ca-certificates \curl \gnupg-agent \software-properties-common添加 Docker 的官方 GPG 密钥 $ curl -fsSL https://download.do…...

Vue-2.1scoped样式冲突
默认情况:写在组件中的样式会全局生效->因此很容易造成多个组件之间的样式冲突问题 1.全局样式:默认组件中的样式会作用到全局 2.局部样式:可以给组件加上scoped属性,可以让样式只作用于当前组件 <style scoped> <…...

Matlab之查询子字符串在字符串中的起始位置函数strfind
一、功能 strfind函数用于在一个字符串中查找指定的子字符串,并返回子字符串在字符串中的起始位置。 二、语法 indices strfind(str, pattern) 其中,str是要进行查找的字符串,pattern是要查找的子字符串。 函数会返回一个由子字符串在字…...

[游戏开发][Unity]安卓出包报错记录
打包报错日志有以下几种类型: 报错: CommandInvokationFailure: Android Asset Packaging Tool failed. E:\Android-SDK-Tool\build-tools\33.0.2\aapt.exe package -v -f -F raw.ap_ -A raw -0 "" --ignore-assets "!.svn:!.git:!.ds_st…...

在两个有序数组中找整体第k小的数
一、题目 给定两个已经排序的数组(假设按照升序排列),然后找出第K小的数。比如数组A {1, 8, 10, 20}, B {5, 9, 22, 110}, 第 3 小的数是 8.。…...
`head` 显示文本文件的开头部分)
Linux 指令心法(十)`head` 显示文本文件的开头部分
文章目录 命令的概述和用途命令的用法命令行选项和参数的详细说明命令的示例命令的注意事项或提示 命令的概述和用途 head 是一个用于显示文本文件的开头部分的命令。它在 Linux 和 Unix 系统中非常有用,因为它允许用户查看文件的前几行,以便快速预览文…...

前端——Layui的导航栏与tab页联动
一、body <!-- 导航栏 --><div class"layui-side layui-bg-black"><div class"layui-side-scroll"><ul id"nav" class"layui-nav layui-nav-tree" lay-filter"stock"><li class"layui-n…...

一致性哈希算法
普通取模算法 假设我们有三台缓存服务器,用于缓存图片,我们为这三台缓存服务器编号为 0号、1号、2号,现在有3万张图片需要缓存,我们希望这些图片被均匀的缓存到这3台服务器上,以便它们能够分摊缓存的压力。也就是说&a…...
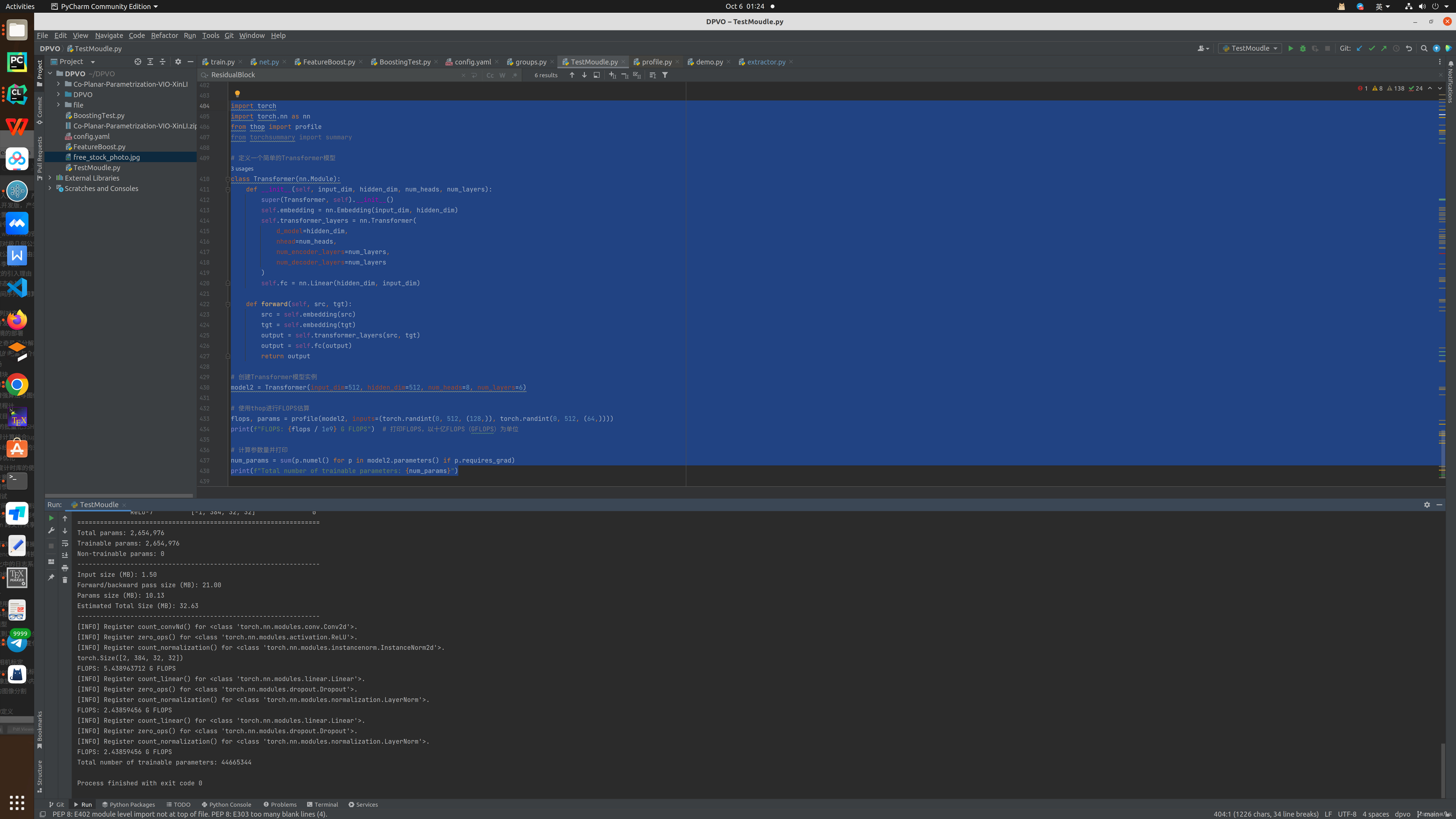
深度学习基础之参数量(3)
一般的CNN网络的参数量估计代码 class ResidualBlock(nn.Module):def __init__(self, in_planes, planes, norm_fngroup, stride1):super(ResidualBlock, self).__init__()print(in_planes, planes, norm_fn, stride)self.conv1 nn.Conv2d(in_planes, planes, kernel_size3, …...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
