35.树与二叉树练习(1)(王道第5章综合练习)
【所用的树,队列,栈的基本操作详见上一节代码】
试题1(王道5.3.3节第3题):
编写后序遍历二叉树的非递归算法。
参考:34.二叉链树的C语言实现_北京地铁1号线的博客-CSDN博客![]() https://blog.csdn.net/qq_54708219/article/details/133581706
https://blog.csdn.net/qq_54708219/article/details/133581706
试题2(王道5.3.3节第4题):
给出二叉树自下而上,从右到左的层次遍历算法。
这道题很显然就是层次遍历算法调个个,加个栈即可实现:
//层次遍历(自下而上,从右到左)
void LevelOrder2(BiTree T){Queue q;InitQueue(q);Sqstack S;InitStack(S);BiTree p = T;InsertQueue(q, p);while(!IsQueueEmpty(q)){p = DeleteQueue(q, p);InsertSqstack(S, p);if(p->lchild!=NULL)InsertQueue(q, p->lchild);if(p->rchild!=NULL)InsertQueue(q, p->rchild);}while(S.top != -1){p = DeleteSqstack(S, p);printf("%c", p->data);}
}输出:
输入二叉树的前序序列,#代表空子树:
ABD##E##C##
二叉树创建成功!
二叉树的层次遍历序列是:ABCDE
二叉树的层次遍历(自下而上,自右向左)序列是:EDCBA试题3(王道5.3.3节第5题):
设计非递归算法求二叉树的高度。
此题采用层次遍历,附设一个指针a:
//利用层次遍历实现非递归计算树的深度
int LevelOrderDepth(BiTree T){int Depth = 0;if(!T)return Depth;else{Queue q;InitQueue(q);BiTree p = T;InsertQueue(q, p);Depth = 1;int a = q.rear; //指针a指向队尾,也就是这一层最后一个元素while(!IsQueueEmpty(q)){if(q.front==a){ //这个时候说明这一层出完了,此时rear就是下一行的末尾结点a = q.rear;Depth = Depth + 1;}p = DeleteQueue(q, p);if(p->lchild!=NULL)InsertQueue(q, p->lchild);if(p->rchild!=NULL)InsertQueue(q, p->rchild);}return Depth;}
}输出:
输入二叉树的前序序列,#代表空子树:
ABD##E##C##
二叉树创建成功!
二叉树的深度是(非递归算法):3试题4(王道5.3.3节第6题):
设一棵二叉树中各结点的值互不相同,其先序遍历序列和中序遍历序列分别存放在两个数组A和B中,试编写算法建立该二叉树的二叉链表。
仍需要采用递归操作,这里要想办法根据前序序列找到根结点,然后在中序序列找根结点,从而确定哪些结点属于左子树,哪些结点属于右子树。
//由先序序列和中序序列建立二叉树
BiTree CreateBiTreeviaOrders(char a[],char b[],int x1,int y1,int x2,int y2){//x1,y1工作在前序序列中,x2,y2工作在中序序列中BiTree T;T = (BiTree)malloc(sizeof(BiTNode));T->data = a[x1]; //前序序列的第一个结点就是根结点int llen, rlen;for (int i = x2; i <= y2; i++){ //在中序序列找根结点if(b[i] == a[x1]){llen = i - x2; //左子树的序列长度(结点个数)rlen = y2 - i; //右子树的序列长度(结点个数)}}if (llen == 0)T->lchild = NULL;elseT->lchild = CreateBiTreeviaOrders(a, b, x1 + 1, x1 + llen, x2, x2 + llen - 1);if (rlen == 0)T->rchild = NULL;elseT->rchild = CreateBiTreeviaOrders(a, b, y1 - rlen + 1, y1, y2 - rlen + 1, y2);return T;
}int main(){BiTree T;char a[6] = {'A', 'B', 'C', 'D', 'E', 'F'}; //先序序列char b[6] = {'C', 'B', 'A', 'E', 'D', 'F'}; //中序序列T = CreateBiTreeviaOrders(a, b, 0, 5, 0, 5); //初始必须是0和数组长度减一printf("该二叉树的后序遍历序列是:");PostOrderTraverse(T); //输出后序序列进行验证return 0;
}这里以王道5.3.3节单选15题进行验证,输出结果就是A选项。
该二叉树的后序遍历序列是:CBEFDA试题5(王道5.3.3节第7题):
二叉树按二叉链表存储,写一个判别给定二叉树是否是完全二叉树的算法。
此题的思路是借助层次遍历和队列,当队列中输出空结点的时候,如果此时队列还有非空结点说明不是完全二叉树。注意这里输入和验证的都是扩展二叉树,所以去掉了层次遍历中的结点非空判断。
//判断是否是完全二叉树
bool IfCompleteTree(BiTree T){Queue q;InitQueue(q);BiTree p = T;if(!p)return true;InsertQueue(q, p);while(!IsQueueEmpty(q)){p = DeleteQueue(q, p);if(p!=NULL){InsertQueue(q, p->lchild);InsertQueue(q, p->rchild);}else{int a = q.front;while(a!=q.rear){if(q.data[a]!=NULL)return false;a = (a + 1) % MAXSIZE;}return true;} }
}int main(){BiTree T;printf("输入二叉树的前序序列,#代表空子树:\n");CreateBiTree(T);printf("二叉树创建成功!\n");printf("该二叉树是否是完全二叉树?%d", IfCompleteTree(T));return 0;
}输出:
输入二叉树的前序序列,#代表空子树:
ABD##E##C##
二叉树创建成功!
该二叉树是否是完全二叉树?1输入二叉树的前序序列,#代表空子树:
AB##CD##E##
二叉树创建成功!
该二叉树是否是完全二叉树?0试题6(王道5.3.3节第8题):
设二叉树采用二叉链表存储结构,设计算法计算给定二叉树的双分支结点个数。
递归算法:
//判断是否是完全二叉树
int TwobranchNodes(BiTree T){if(T==NULL)return 0;else if(T->lchild!=NULL&&T->rchild!=NULL)return TwobranchNodes(T->lchild) + TwobranchNodes(T->rchild) + 1;elsereturn TwobranchNodes(T->lchild) + TwobranchNodes(T->rchild);
}非递归算法(层次遍历逐个结点检查):
//判断是否是完全二叉树
int TwobranchNodes(BiTree T){int a = 0;Queue q;InitQueue(q);BiTree p = T;InsertQueue(q, p);while(!IsQueueEmpty(q)){p = DeleteQueue(q, p);if(p->lchild!=NULL && p->rchild!=NULL)a = a + 1;if(p->lchild!=NULL)InsertQueue(q, p->lchild);if(p->rchild!=NULL)InsertQueue(q, p->rchild);}return a;
}试题7(王道5.3.3节第9题):
设树B是一棵采用链式结构存储的二叉树,编写一个把树B中所有结点的左右子树进行交换的函数。
此题同题6一样也可以用递归或层次遍历的方法,这里给出非递归的方法:
//把二叉树的左右子树交换
int ChangeTwobranch(BiTree &T){Queue q;InitQueue(q);BiTree p = T;BiTree r;InsertQueue(q, p);while(!IsQueueEmpty(q)){p = DeleteQueue(q, p);if(p->lchild!=NULL || p->rchild!=NULL){r = p->lchild;p->lchild = p->rchild;p->rchild = r;}if (p->lchild != NULL)InsertQueue(q, p->lchild);if(p->rchild!=NULL)InsertQueue(q, p->rchild);}return 0;
}输出:
输入二叉树的前序序列,#代表空子树:
ABD##E##C##
二叉树创建成功!
该二叉树的层次遍历序列是:ACBED试题8(王道5.3.3节第10题):
假设二叉树采用二叉链存储结构存储,设计算法求先序遍历序列中第k个结点的值。
这里使用一个计数器即可:
//输出前序遍历的第x个元素
void PreOrderx(BiTree T,int x){int a = 0;BiTree p = T; //p是遍历指针Sqstack S;InitStack(S);while(p != NULL|| !IsStackEmpty(S)){if(p){a = a + 1;if(a == x){printf("第%d个元素是:%c", x, p->data);break;} InsertSqstack(S, p);p = p->lchild;}else{p = DeleteSqstack(S, p);p = p->rchild;}}
}当然也可以采用递归,注意这里的计数器必须写在全局变量里,否则每次调用递归都会从零开始:
//输出前序遍历的第x个元素
int a = 0; //计数器
void PreOrderx(BiTree T,int x){if (T!=NULL){a = a + 1;if(a==x)printf("前序遍历序列的第%d个元素是:%c", x, T->data);PreOrderx(T->lchild,x);PreOrderx(T->rchild,x);}
}int main(){BiTree T;printf("输入二叉树的前序序列,#代表空子树:\n");CreateBiTree(T);printf("二叉树创建成功!\n");PreOrderx(T, 3);return 0;
}输出:
输入二叉树的前序序列,#代表空子树:
ABD##E##C##
二叉树创建成功!
前序遍历序列的第3个元素是:D试题9(王道5.3.3节第11题):
已知二叉树以二叉链表存储,编写算法完成:对于树中的每个值为x的结点,删去以它为根的子树,并释放相应空间。
仍然是与层次遍历结合:
//这个函数用来删除树T
void Free(BiTree &T){if(T!=NULL){Free(T->lchild);Free(T->rchild);free(T);}
}//对值为x的结点,删除以它为根的子树
void Freex(BiTree &T,char x){Queue q;InitQueue(q);BiTree p = T;InsertQueue(q, p);while(!IsQueueEmpty(q)){p = DeleteQueue(q, p);if(p->data == x){Free(p->lchild); //这样写保留了当前结点Free(p->rchild);p->lchild = NULL;p->rchild = NULL;}if(p->lchild!=NULL)InsertQueue(q, p->lchild);if(p->rchild!=NULL)InsertQueue(q, p->rchild);}
}int main(){BiTree T;printf("输入二叉树的前序序列,#代表空子树:\n");CreateBiTree(T);printf("二叉树创建成功!\n");printf("当前二叉树的层次遍历序列是:");LevelOrder(T);printf("\n");Freex(T, 'B'); //删除以B为根结点的树printf("当前二叉树的层次遍历序列是:");LevelOrder(T);printf("\n");return 0;
}输出:
输入二叉树的前序序列,#代表空子树:
ABD##E##C##
二叉树创建成功!
当前二叉树的层次遍历序列是:ABCDE
当前二叉树的层次遍历序列是:ABC输入二叉树的前序序列,#代表空子树:
ABD###CE##F##
二叉树创建成功!
当前二叉树的层次遍历序列是:ABCDEF
当前二叉树的层次遍历序列是:ABCEF试题10(王道数据结构5.3.3节第12题):
编写算法打印值为x的结点的所有祖先,假设值为x的结点不多于一个。
此题的算法十分典型:它用的是非递归后序遍历算法,这种算法需要借助栈来实现,当访问到值为x的结点的时候,栈中所有元素就是该结点的祖先,依次打印输出即可。有关非递归后序遍历算法的代码在上一节。
//寻找给定结点的所有祖先结点,采用后续遍历的非递归算法
void FindParents(BiTree T,char x){Sqstack S;InitStack(S);BiTree p = T;BiTree r = NULL; //r用来记录访问结点的前一个结点while(p||!IsStackEmpty(S)){if(p){InsertSqstack(S, p);p = p->lchild;}else{p = S.data[S.top]; //读栈顶元素(但不出栈)if(p->rchild&&p->rchild!=r){p = p->rchild;}else{p = DeleteSqstack(S, p);if(p->data == x){printf("%c", p->data);break;}r = p;p = NULL;}}}while(!IsStackEmpty(S)){ //这个时候栈里的元素全部是结点的祖先p = DeleteSqstack(S, p);printf("%c", p->data);}
}int main(){BiTree T;printf("输入二叉树的前序序列,#代表空子树:\n");CreateBiTree(T);printf("二叉树创建成功!\n");printf("当前二叉树的层次遍历序列是:");LevelOrder(T);printf("\n");printf("当前二叉树中结点E的祖先结点是:");FindParents(T, 'E');return 0;
}输出:
输入二叉树的前序序列,#代表空子树:
ABD##E##C##
二叉树创建成功!
当前二叉树的层次遍历序列是:ABCDE
当前二叉树中结点E的祖先结点是:EBA试题11(王道数据结构5.3.3节第13题):
给出二叉链树中两个结点的指针p和q,试编写算法求解p和q的公共祖先结点r。
此题和上一题很像,分别求出p和q的祖先然后比较即可。
//寻找给定结点的所有祖先结点,采用后续遍历的非递归算法,和上一题不同的是,本题以栈的形式返回
Sqstack FindParents(BiTree T,char x){Sqstack S;InitStack(S);BiTree p = T;BiTree r = NULL; //r用来记录访问结点的前一个结点while(p||!IsStackEmpty(S)){if(p){InsertSqstack(S, p);p = p->lchild;}else{p = S.data[S.top]; //读栈顶元素(但不出栈)if(p->rchild&&p->rchild!=r){p = p->rchild;}else{p = S.data[S.top];if(p->data == x){break;}p = DeleteSqstack(S, p);r = p;p = NULL;}}}return S;
}
//有了两个栈我们就可以遍历然后找到祖先结点了
//注意这里最差也能返回整棵二叉树的根结点,或者返回其中一个结点时,代表一个结点就是另一个结点的祖先
BiTree FindSameParents(BiTree T,char a,char b){Sqstack S1 = FindParents(T, a);Sqstack S2 = FindParents(T, b);int same = -1; //same用来遍历两个栈,并指向最后一个相同的祖先结点while(S1.data[same+1] == S2.data[same+1]){same = same + 1;}printf("%c", S1.data[same]->data);return S1.data[same];
}int main(){BiTree T;printf("输入二叉树的前序序列,#代表空子树:\n");CreateBiTree(T);printf("二叉树创建成功!\n");printf("当前二叉树的层次遍历序列是:");LevelOrder(T);printf("\n");printf("当前二叉树中结点E,F的祖先结点是:");FindSameParents(T, 'E', 'F'); //求E,F的祖先结点return 0;
}输出:
输入二叉树的前序序列,#代表空子树:
ABD###CE##F##
二叉树创建成功!
当前二叉树的层次遍历序列是:ABCDEF
当前二叉树中结点E,F的祖先结点是:C试题12(王道数据结构5.3.3节第14题):
假设二叉树采用二叉链表存储,设计一个算法求非空二叉树的宽度(也就是结点数最多的那一层的结点个数)。
此题仍然可以利用层次遍历把每层的结点数输出,存在一个数组里面然后找出最大值:
//求非空二叉树的宽度,借助层次遍历把每层的结点数都求出来
int LevelOrderWidth(BiTree T){Queue q;InitQueue(q);BiTree p = T;InsertQueue(q, p);int a = q.front; //a指针指向这一层的第一个结点int b = q.rear; //b指针指向这一层的第一个结点int num = 1; //输出这一层的结点个数int numarray[10]; //把各层的结点个数存在一个数组里int depth = 0; //深度,实际深度是depth+1,因为numarray数组下标从0开始numarray[depth] = num;while(!IsQueueEmpty(q)){if(q.front == b){ //说明这一层出完了a = q.front; //a指向下一层第一个结点b = q.rear; //b指向下一层最后一个结点num = (b - a > 0) ? (b - a) : (b - a + MAXSIZE); //循环队列三目运算符判断depth = depth + 1;numarray[depth] = num;}p = DeleteQueue(q, p);if(p->lchild!=NULL)InsertQueue(q, p->lchild);if(p->rchild!=NULL)InsertQueue(q, p->rchild);}//到此numarray存储了每层的结点数,接下来找其中的最大值输出num = 1;for (int i = 0; i <= depth;i++){printf("%d", numarray[i]);if(numarray[i] > num)num = numarray[i];}return num;
}int main(){BiTree T;printf("输入二叉树的前序序列,#代表空子树:\n");CreateBiTree(T);printf("二叉树创建成功!\n");printf("当前二叉树的层次遍历序列是:");LevelOrder(T);printf("\n");printf("各层的结点数是:");printf("二叉树的宽度是:%d",LevelOrderWidth(T));return 0;
}输出:
输入二叉树的前序序列,#代表空子树:
ABDF##G##E##CH###
二叉树创建成功!
当前二叉树的层次遍历序列是:ABCDEHFG
各层的结点数是:1232二叉树的宽度是:3相关文章:
35.树与二叉树练习(1)(王道第5章综合练习)
【所用的树,队列,栈的基本操作详见上一节代码】 试题1(王道5.3.3节第3题): 编写后序遍历二叉树的非递归算法。 参考:34.二叉链树的C语言实现_北京地铁1号线的博客-CSDN博客https://blog.csdn.net/qq_547…...

JSON数据处理工具-在线工具箱网站tool.qqmu.com的使用指南
导语:无论是处理JSON数据、进行文本数字处理、解码加密还是使用站长工具,我们都希望能够找到一个功能强大、简便易用的在线平台。tool.qqmu.com作为一款瑞士军刀般的在线工具箱网站,满足了众多用户的需求。本文将介绍tool.qqmu.com的多项功能…...
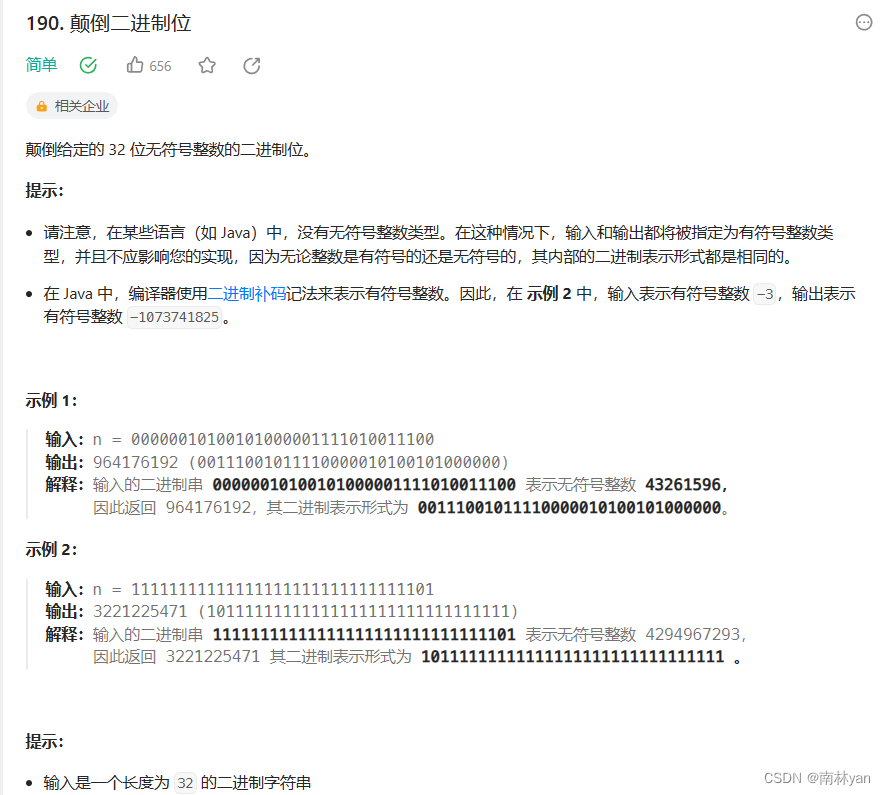
leetcode:190. 颠倒二进制位
一、题目: 函数原型: uint32_t reverseBits(uint32_t n) 解释:uint32是无符号int或short的别称,传入的参数是一个32位二进制串,返回值是该32位二进制串逆序后的十进制值 二、思路: 实际上并不需要真的去逆…...

Spring Cloud--@RefreshScope动态刷新的注意事项
原文网址:Spring Cloud--RefreshScope动态刷新的注意事项_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Spring Cloud的RefreshScope动态刷新的注意事项。 不用RefreshScope也能动态刷新 Spring Cloud的默认实现了动态刷新,不加RefreshScope就能实现动态…...

visual-studio-code通过跳板机连接远程服务器的配置操作
step1:在本机上生成私钥和公钥 sh-keygen -t rsa -C “your_emailxxx.com”生成的两个默认文件中,id_rsa.pub是公钥,id_rsa是私钥 step2:在vscode安装Remote-SSH插件 step3:将本机生成的私钥和公钥上传服务器上 把本机生成的rsa_id.pub公钥上传至服务…...
-- gpio - GPIO操作)
LuatOS-SOC接口文档(air780E)-- gpio - GPIO操作
常量 常量 类型 解释 gpio.LOW number 低电平 gpio.HIGH number 高电平 gpio.PULLUP number 上拉 gpio.PULLDOWN number 下拉 gpio.RISING number 上升沿触发 gpio.FALLING number 下降沿触发 gpio.BOTH number 双向触发,部分设备支持 gpio.HIGH_IRQ …...
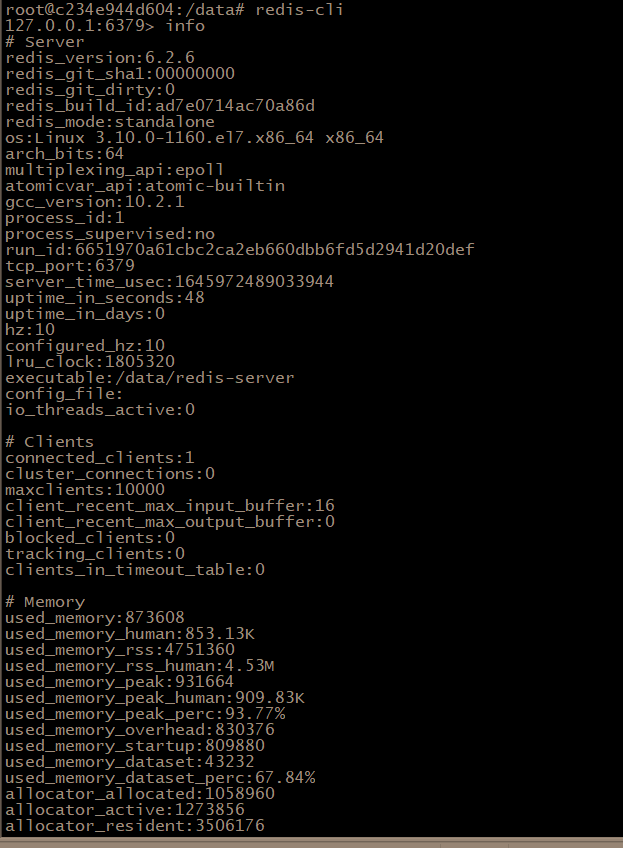
一个命令让redis服务端所有信息无所遁形~(收藏吃灰系列)
Redis服务器是一个事件驱动程序,它主要处理两类事件:文件事件和时间事件。这些事件的处理和Redis命令的执行密切相关。下面我将以Redis服务端命令为切入点,深入解析其工作原理和重要性。 首先,我们先了解Redis服务端有哪些命令。…...

通过Node.js获取高德的省市区数据并插入数据库
通过Node.js获取高德的省市区数据并插入数据库 1 创建秘钥1.1 登录高德地图开放平台1.2 创建应用1.3 绑定服务创建秘钥 2 获取数据并插入2.1 创建数据库连接工具2.2 请求数据2.3 数据处理2.4 全部代码 3 还可以打印文件到本地 1 创建秘钥 1.1 登录高德地图开放平台 打开开放平…...
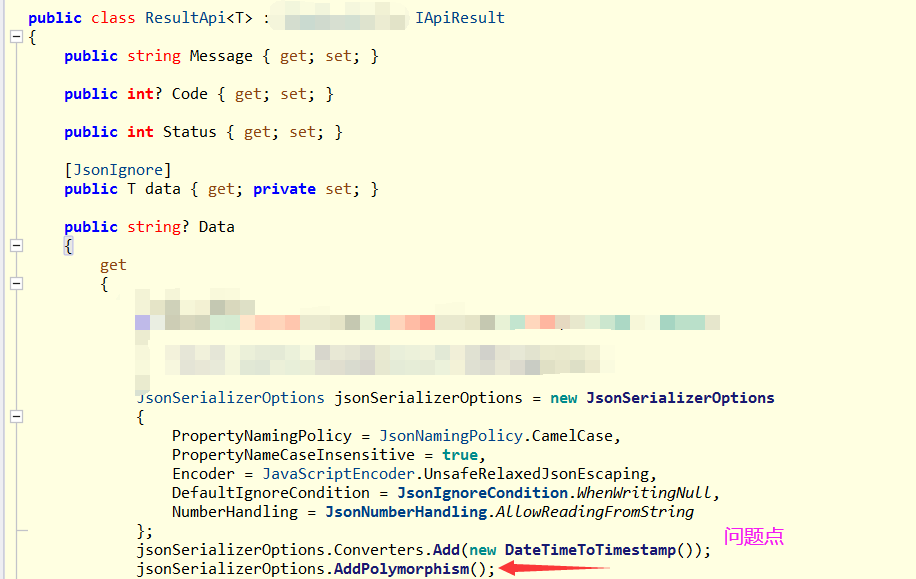
记一次 .NET某账本软件 非托管泄露分析
一:背景 1. 讲故事 中秋国庆长假结束,哈哈,在老家拍了很多的短视频,有兴趣的可以上B站观看:https://space.bilibili.com/409524162 ,今天继续给大家分享各种奇奇怪怪的.NET生产事故,希望能帮助…...
Oracle笔记-对ROWNUM的一次理解(简单分页)
此博文记录时间:2023-05-05,发到互联网上是2023-10-09 这个在分页里面用得比较多,在MySQL中,通常使用limit去操作,而去感觉比较简单,Oracle中无此关键字。 通过查阅资料后,要实现分页需要用到…...

系统架构设计:10 论数据湖技术及其应用
目录 一 数据湖技术 1 数据库 2 数据仓库 3 数据库与数据仓库的对比 4 数据湖...

【MySQL】基本查询(三)聚合函数+group by
文章目录 一. 聚合函数二. group by子句结束语 建立如下表 //创建表结构 mysql> create table exam_result(-> id int unsigned primary key auto_increment,-> name varchar(20) not null comment 同学姓名,-> chinese float default 0.0 comment 语文成绩,->…...
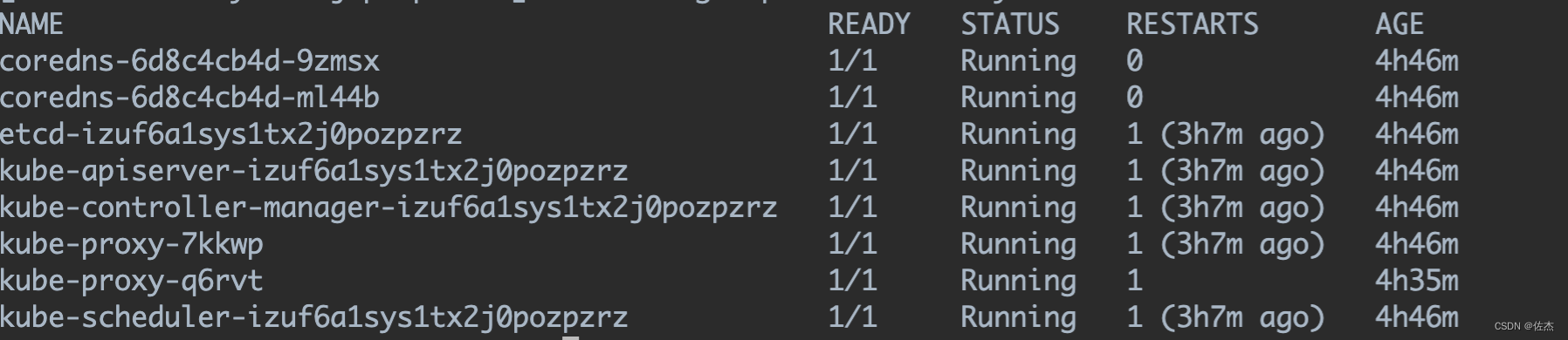
基于KubeAdm搭建多节点K8S集群
基于KubeAdm搭建多节点K8S集群 1、基本流程(注意 docker 版本和kubeadm、kubelet、kubectl的关系)2、安装utils依赖(安装范围:主节点工作节点)3、安装docker (安装范围:主节点工作节点ÿ…...

VuePress实现自动获取文章侧边栏目录功能
👨🏻💻 热爱摄影的程序员 👨🏻🎨 喜欢编码的设计师 🧕🏻 擅长设计的剪辑师 🧑🏻🏫 一位高冷无情的编码爱好者 大家好,我是 DevO…...
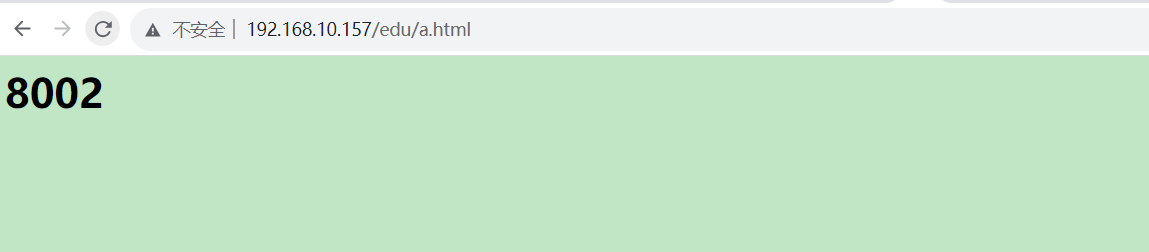
nginx配置实例-负载均衡
1 实现效果: 浏览器访问nginx,输入访问nginx地址,然后负载均衡到tomcat8080和8002端口中 2 准备工作: 1)准备两台tomcat容器,一台8080,一台8081 2)在两台tomcat里面的webapps目录…...

Nginx的跨域问题解决
同源策略 浏览器的同源策略:是一种约定,是浏览器最核心也是最基本的安全功能,如果浏览器少了同源策略,则浏览器的正常功能可能都会受到影响。 同源: 协议、域名(IP)、端口相同即为同源 跨域问题 有两台服务器分别为A,B,如果从…...

ts的交叉类型是什么
交叉类型是TypeScript中的一种类型操作符,用于将多个类型合并成一个类型,表示同时拥有这些类型的属性和方法。交叉类型使用&符号进行连接。例如,以下代码定义了一个交叉类型Person & Serializable: interface Person {na…...

【【萌新的SOC学习之AXI接口简介】】
萌新的SOC学习之AXI接口简介 AXI总线的初步介绍 AXI 总线是 ARM AMBA 一部分 (高级可扩展接口) AMBA(高级微控制器总线架构) :开放的片内互联的总线标准,能再多主机设计中实现多个控制器和外围设备之间的连接和管理。…...

ios safari 浏览器跳转页面没有自适应
今天开发遇到了一个问题,当用户点击浏览器中的表单进行注册时,表单元素会放大,随后跳转页面无法还原到初始状态。 这是因为如果 的 font-size 被设定为 16px 或更大,那么 iOS 上的 Safari 将正常聚焦到输入表单中。但是ÿ…...

node、npm、nvm相关概念区别
node:一个基于Chrome V8引擎的JavaScript运行环境,让JavaScript 运行在服务端的开发平台。 nvm:node.js 版本管理工具。不同项目可能需要不同版本的 node,可以使用 nvm 来管理 node.js 版本。 安装教程参考 nvm下载及详细安装教程…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
