【数据结构】树和二叉树概念及其结构
目录
一 树概念及结构
1 树的概念
2 树的相关概念
3 树的表示
二 二叉树概念及结构
1 概念
2 特殊二叉树
3 二叉树的性质
一 树概念及结构
1 树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点
除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
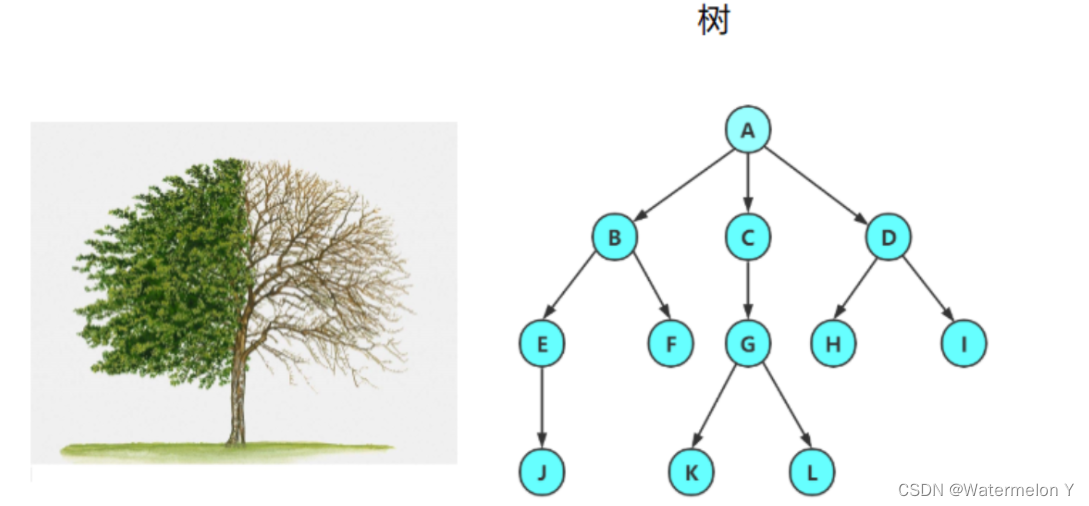
2 树的相关概念

节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m > 0)棵互不相交的树的集合称为森林;
3 树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间 的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法 等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
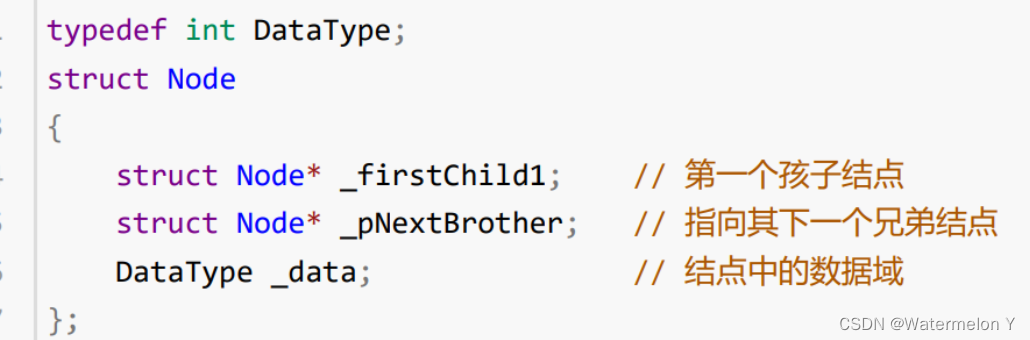
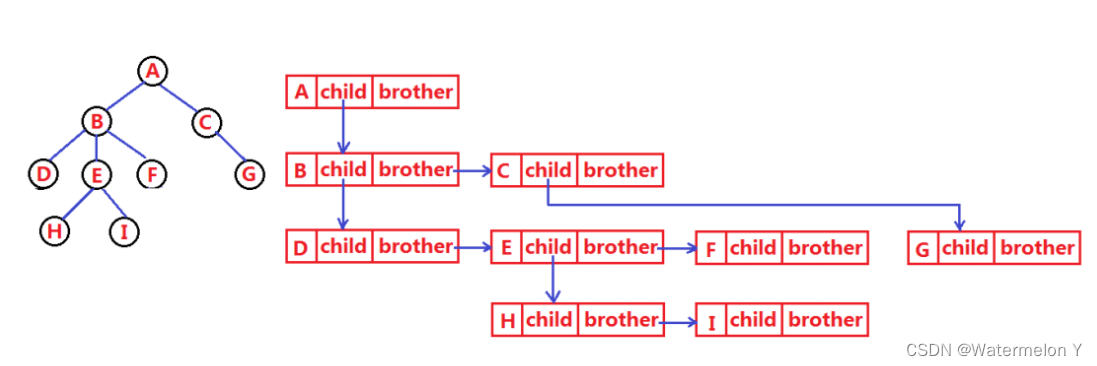 二 二叉树概念及结构
二 二叉树概念及结构
1 概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
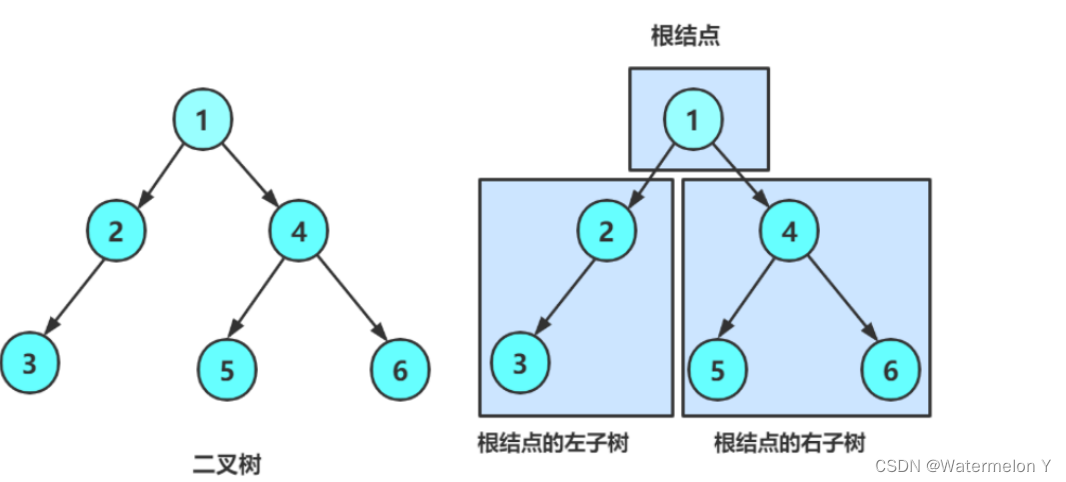
从上图可以看出:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
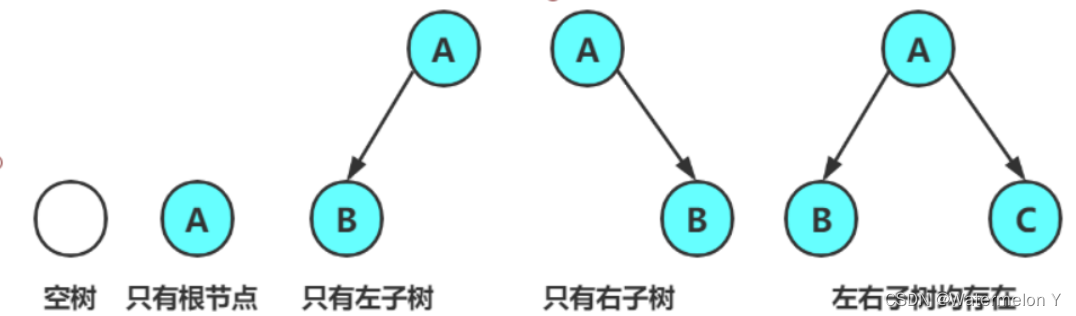
2 特殊二叉树
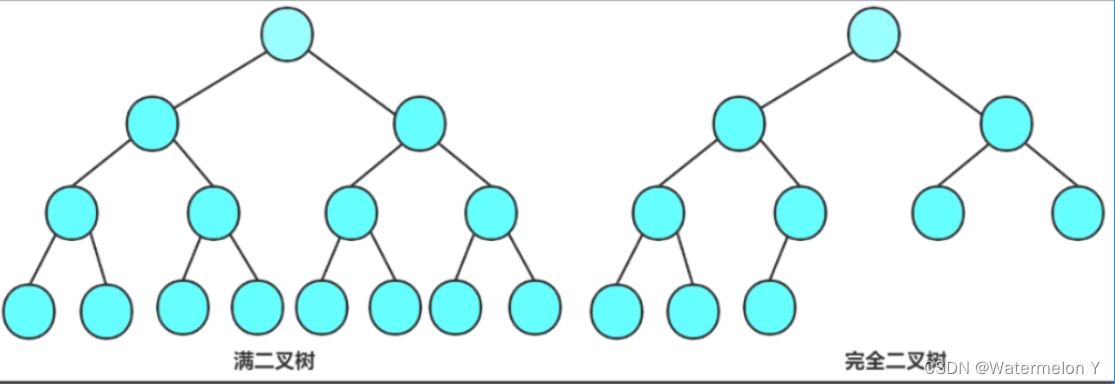
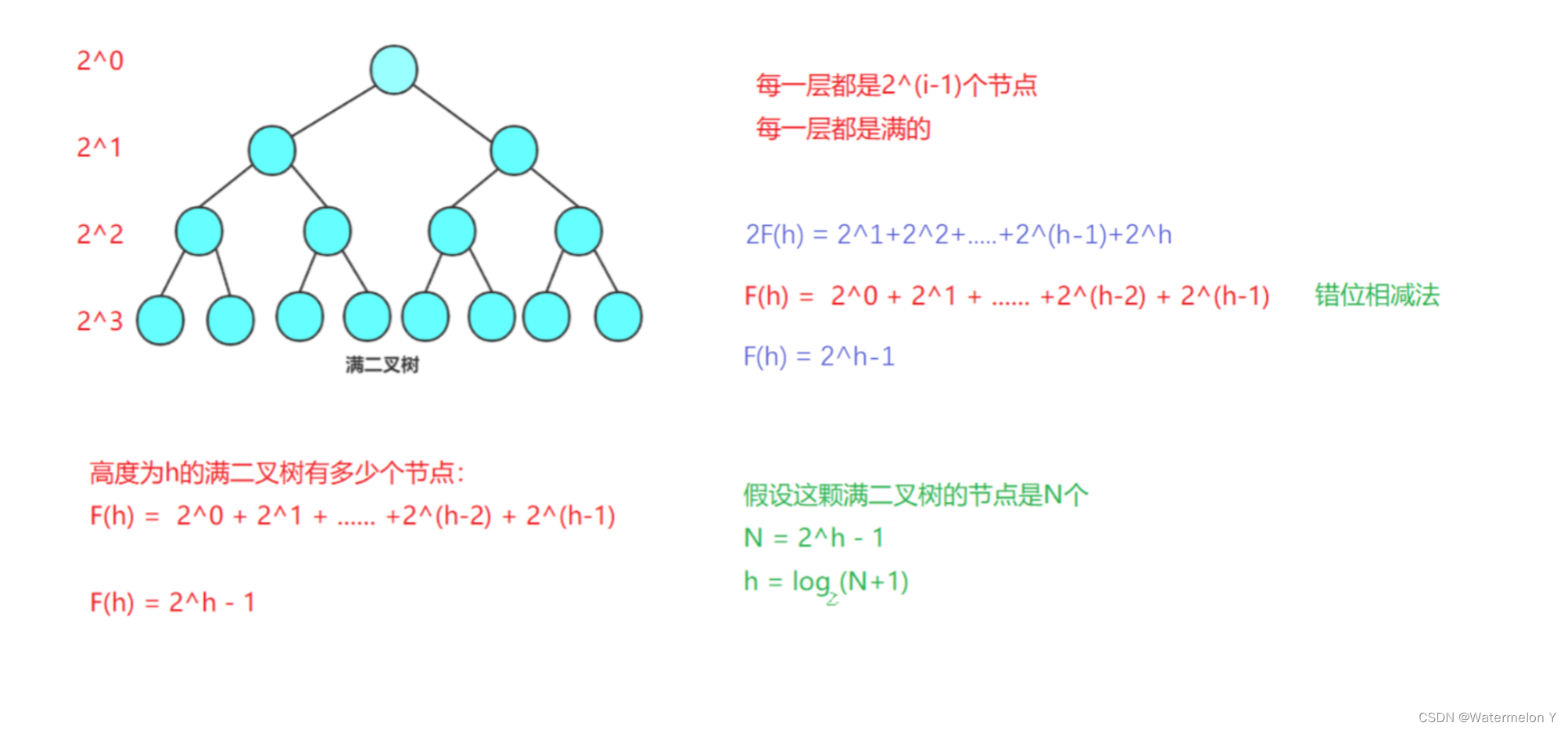
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是 说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
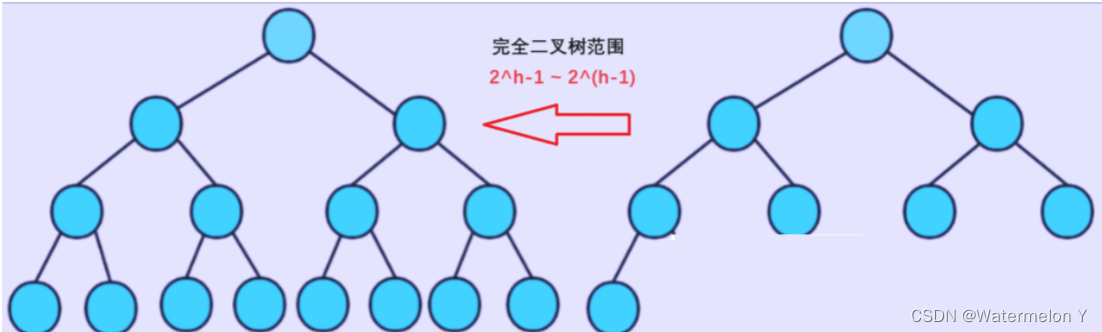
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K 的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对 应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
3 二叉树的性质

1. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2. 若2i+1=n否则无左孩子
3. 若2i+2=n否则无右孩子
相关文章:

【数据结构】树和二叉树概念及其结构
目录 一 树概念及结构 1 树的概念 2 树的相关概念 3 树的表示 二 二叉树概念及结构 1 概念 2 特殊二叉树 3 二叉树的性质 一 树概念及结构 1 树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集…...

刘京城:我的《软件方法》学习经历(有彩蛋)
DDD领域驱动设计批评文集 做强化自测题获得“软件方法建模师”称号 《软件方法》各章合集 写在前面(潘加宇) 下面是刘京城写的关于他学习《软件方法》的经历。我在前面啰嗦几句。 我做软件建模方面的研究和普及工作已经24年了,和各行各业…...

浏览器详解(四) 渲染
大家好,我是半虹,这篇文章来讲浏览器渲染 1、基本介绍 浏览器是多进程多线程的架构,包括有浏览器进程、渲染器进程、GPU 进程、插件进程等 在上篇文章中我们介绍过浏览器进程,作为浏览器主进程,负责浏览器基本界面的…...
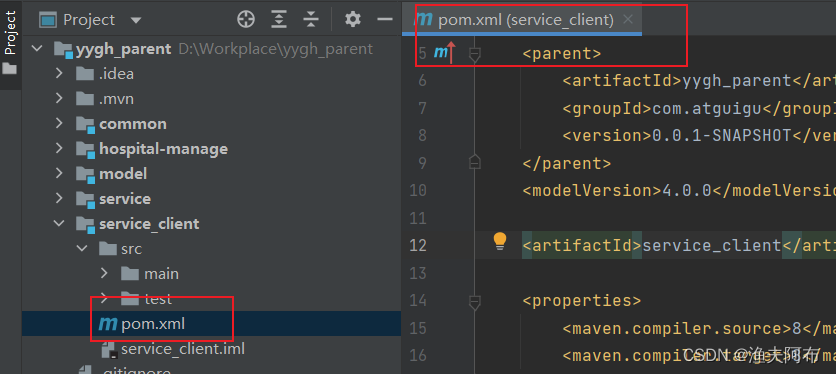
idea新建一个module时,文件夹显示灰色/pom.xml文件显示灰色且中间有条横线
1.问题 2.解决方法 File->Settings->Ignored Files->找到勾选的pom.xml文件,取消勾选,点击ok即可。 3.已解决...

NoSQL数据库(林子雨慕课课程)
文章目录 5.1 NoSQL数据库5.2 NoSQL和关系数据库的比较5.3 四大类型NoSQL数据库5.3.1 键值数据库和列族数据库5.3.2 文档数据库、图数据库、以及不同数据库比较分析 5.4 NoSQL数据库的理论基石CAP理论:BASE理论:Eventual consistency(最终一致…...

模拟器运行在AndroidStudio内部,设置其独立窗口显示
在窗口内部运行 设置成独立窗口 Android Studio->Settings或Preferences->Tools->Emulator->取消勾选Launch in the Running Devices tool window --->点击右下角的OK按钮 ---> 重启Android Studio 再次启动模拟器...
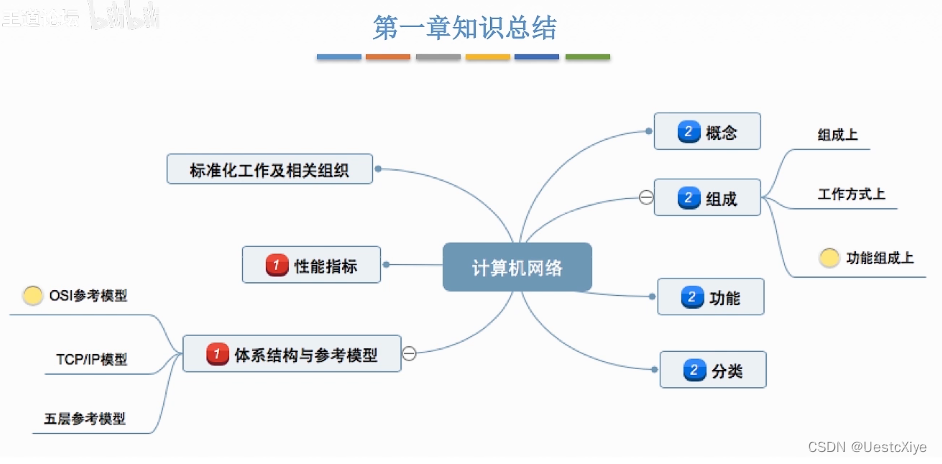
计算机网络 | 体系结构
计算机网络 | 体系结构 计算机网络 | 体系结构概念及功能计算机网络简介计算机网络的功能因特网发展阶段小结 组成与分类计算机网络的组成计算机网络的分类小结 标准化工作及相关组织速率相关性能指标速率带宽吞吐量小结 时延相关性能指标时延时延带宽积往返时延RTT利用率小结 …...
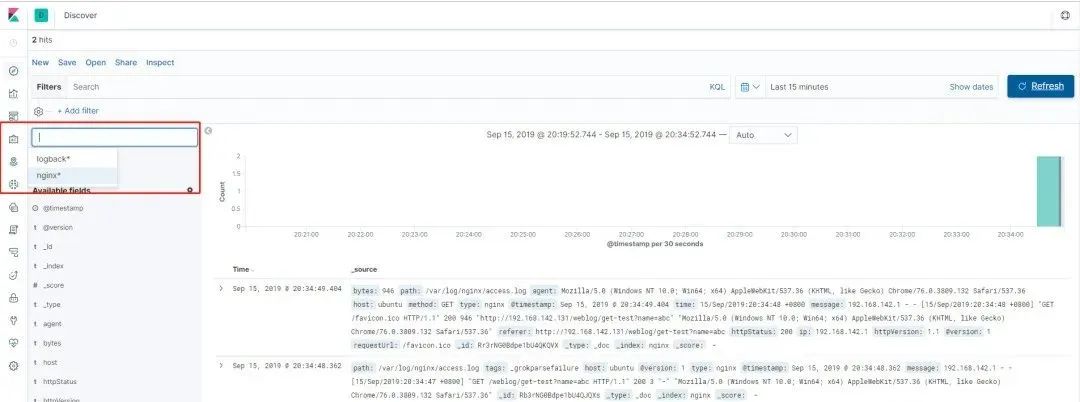
ELK 处理 SpringCloud 日志
在排查线上异常的过程中,查询日志总是必不可缺的一部分。现今大多采用的微服务架构,日志被分散在不同的机器上,使得日志的查询变得异常困难。工欲善其事,必先利其器。如果此时有一个统一的实时日志分析平台,那可谓是雪…...

mac使用python递归删除文件夹下所有的.DS_Store文件
import osfolder_path "yourself file path"for root, dirs, files in os.walk(folder_path):for filename in files:if filename .DS_Store:file_path os.path.join(root, filename)os.remove(file_path)print("delete ok")...

Gitlab+Jenkins自动化部署,解放双手
项目打包 在部署项目前需要对源码进行打包,一个简单的SpringBoot项目默认是打包为jar包,也就是在pom.xml中的<packaging>jar</packaging>方式,当然也会有一些打包成war包方式,使用外置的Tomcat应用服务器部署war包…...
NNDL:作业3
在Softmax回归的风险函数(公式(3.39))中如果加上正则化项会有什么影响? (1) 在 Softmax 回归的风险函数中加入正则化项会对模型的训练产生影响。正则化项的作用是对模型的复杂度进行惩罚,防止过拟合的发生。 (2) 原书公式为: 在加入正则化后损失函数…...

dockers --cap-add 哪些值可以设置
--cap-add 参数可以用于向 Docker 容器添加不同的权限。除了 NET_ADMIN,还有一些其他常用的权限值,包括: SYS_ADMIN:添加系统管理员权限,允许容器内的进程执行系统级别的管理操作,如挂载文件系统、设置时间…...

golang常用库之-HTTP客户端请求库 grequests
文章目录 golang常用库之-HTTP客户端请求库 grequests什么是grequests使用 golang常用库之-HTTP客户端请求库 grequests 什么是grequests 官网:github.com/levigross/grequests A Go “clone” of the great and famous Requests library Go语言的grequests库是一…...
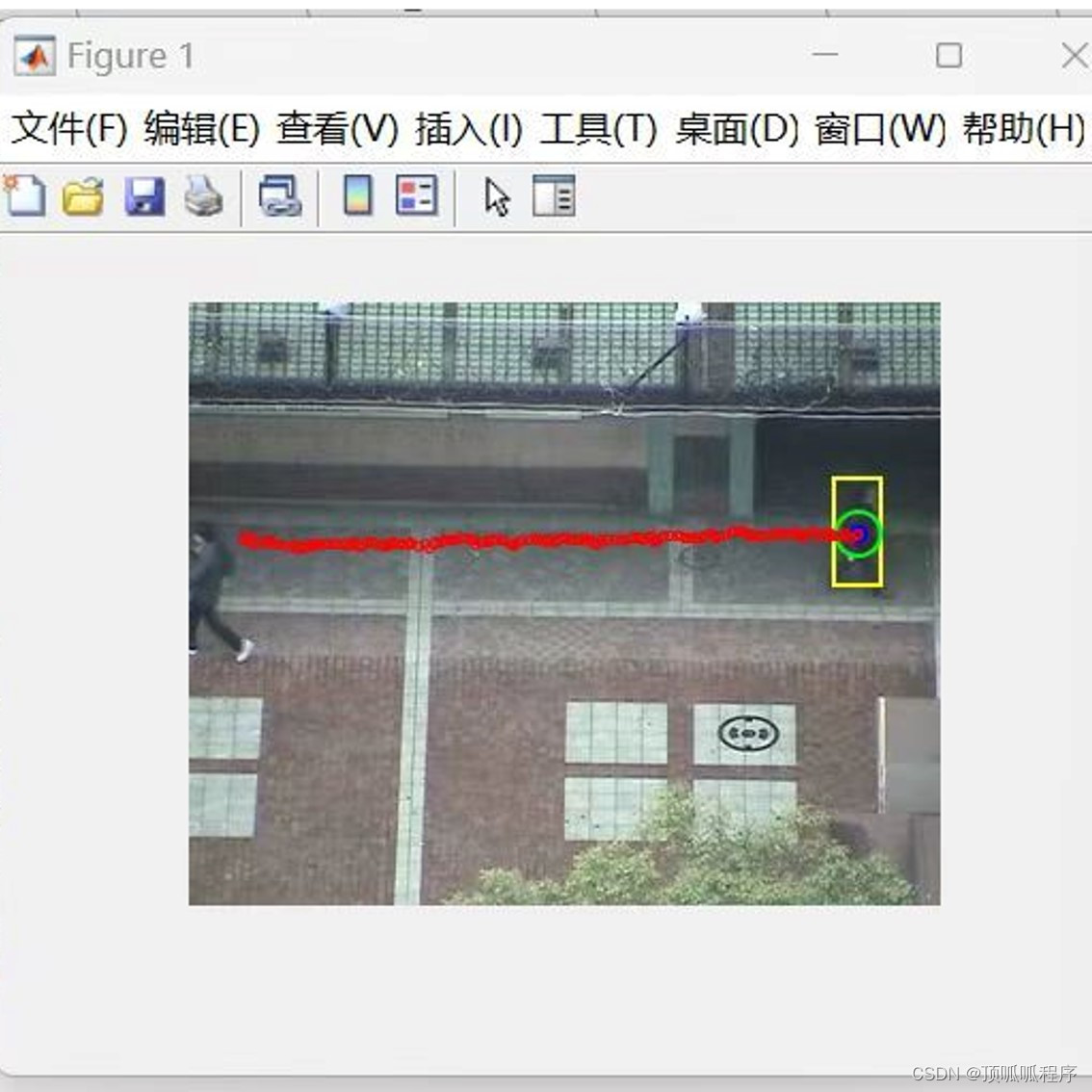
17基于matlab卡尔曼滤波的行人跟踪算法,并给出算法估计误差结果,判断算法的跟踪精确性,程序已调通,可直接运行,基于MATLAB平台,可直接拍下。
17基于matlab卡尔曼滤波的行人跟踪算法,并给出算法估计误差结果,判断算法的跟踪精确性,程序已调通,可直接运行,基于MATLAB平台,可直接拍下。 17matlab卡尔曼滤波行人跟踪 (xiaohongshu.com)...
SpringCloud之Stream框架集成RocketMQ消息中间件
Spring Cloud Stream 是一个用来为微服务应用构建消息驱动能力的框架。它可以基于 Spring Boot 来创建独立的、可用于生产的 Spring 应用程序。Spring Cloud Stream 为一些供应商的消息中间件产品提供了个性化的自动化配置实现,并引入了发布-订阅、消费组、分区这三…...

与创新者同行!Apache Doris 首届线下峰会即将开启,最新议程公开!|即刻预约
点击此处 即刻报名 Doris Summit Asia 2023 回顾人类的发展史,地球起源于 46 亿年前的原始星云、地球生命最初出现于 35 亿年前的原始海洋、人类物种诞生于数百万年前,而人类生产力的真正提升源于十八世纪六十年代的工业革命,自此以后&#…...
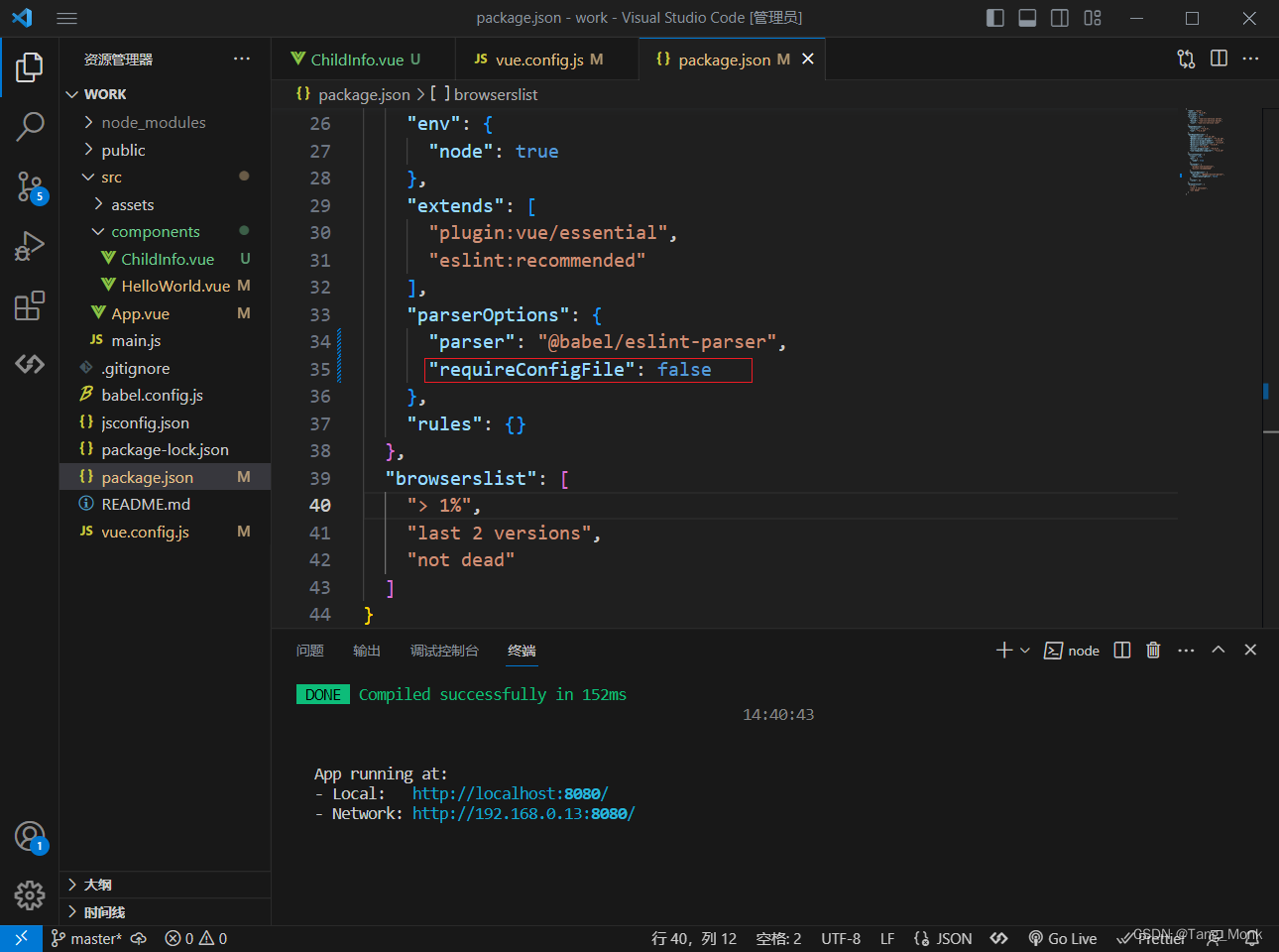
vue解决:Parsing error: No Babel config file detected for ....
报错信息 Parsing error: No Babel config file detected for C:\Users\Admin\Desktop\shabi\work\src\App.vue. Either disable config file checking with requireConfigFile: false, or configure Babel so that it can find the config files. 分析错误:没有检测…...
算法题:K 次取反后最大化的数组和(典型的贪心算法问题)
这道题没有看题解,直接提交,成绩超越99.5%,说明思路是优的。就是考虑的情况里面弯弯绕比较多,需要考虑全面一点。(本题完整题目附在了最后面) 具体思路如下: 1、首先排序,然后从最…...

Go语言中向[]byte数组中增加一个元素
要向http.Request的body中添加一个键值对,可以先将其转换为一个map,然后对其进行修改,最后再将其转回为byte数组。 以下是一个示例代码: import ("net/http""io/ioutil""encoding/json" )type Re…...

CSS 布局案例: 2行、多行每行格数不定,最后一列对齐
布局期望的效果如下: 第二行最后一格与第一行最后一格对齐。每行格数不定。自动拉伸填充整个宽度 实现: 一开始打算用display:flex, 自动分散,但是第二行对齐第一行最后一格控制不了。 使用grid fr均分单位控制。 <!DOCTYPE…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
