当前位置： 首页 > news >正文

NNDL:作业3

news 文章来源：https://blog.csdn.net/weixin_61838030/article/details/133756832 2025/5/6 18:11:51

在Softmax回归的风险函数(公式(3.39))中如果加上正则化项会有什么影响?

(1)

在 Softmax 回归的风险函数中加入正则化项会对模型的训练产生影响。正则化项的作用是对模型的复杂度进行惩罚，防止过拟合的发生。

(2)

原书公式为：

                                        R(W)=-\frac{1}{N}\sum_{n=1}^{N}(y^{(n)})^{T}log\hat{y}^{(n)}

在加入正则化后损失函数为：

                                R(W)=-\frac{1}{N}\sum_{n=1}^{N}(y^{(n)})^{T}log\hat{y}^{(n)}+\lambda W^{T}W

求梯度得：

                              \frac{\partial R(W)}{\partial W}=-\frac{1}{N}\sum_{n=1}^{N}(\hat{y}^{(n)}-y^{(n)})x^{(n)}+2\lambda W

W更新:

                             W=W+\alpha \frac{1}{N}\sum_{n=1}^{N}(\hat{y}^{(n)}-y^{(n)})x^{(n)}-2\lambda W

加入正则化后，在更新参数时每次需要减去2\lambda W，使得参数不会太大，防止数值溢出。

相关文章：

NNDL:作业3

在Softmax回归的风险函数(公式(3.39))中如果加上正则化项会有什么影响? (1) 在 Softmax 回归的风险函数中加入正则化项会对模型的训练产生影响。正则化项的作用是对模型的复杂度进行惩罚，防止过拟合的发生。 (2) 原书公式为： 在加入正则化后损失函数…...

编程日记 2023/10/11 6:08:54

dockers --cap-add 哪些值可以设置

--cap-add 参数可以用于向 Docker 容器添加不同的权限。除了 NET_ADMIN，还有一些其他常用的权限值，包括： SYS_ADMIN：添加系统管理员权限，允许容器内的进程执行系统级别的管理操作，如挂载文件系统、设置时间…...

编程日记 2023/10/11 6:07:53

golang常用库之-HTTP客户端请求库 grequests

文章目录 golang常用库之-HTTP客户端请求库 grequests什么是grequests使用 golang常用库之-HTTP客户端请求库 grequests 什么是grequests 官网：github.com/levigross/grequests A Go “clone” of the great and famous Requests library Go语言的grequests库是一…...

编程日记 2023/10/11 6:05:51

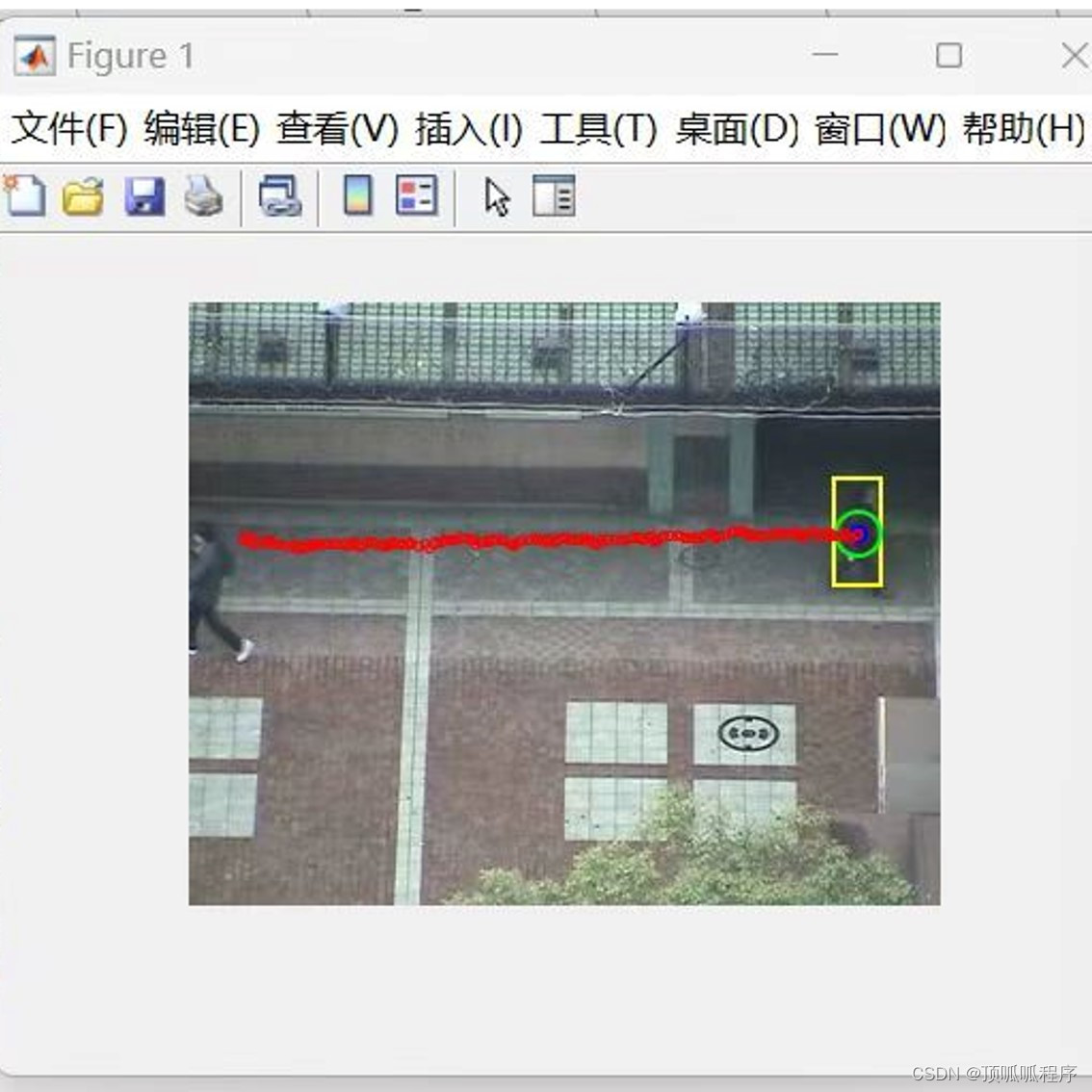
17基于matlab卡尔曼滤波的行人跟踪算法，并给出算法估计误差结果，判断算法的跟踪精确性，程序已调通，可直接运行，基于MATLAB平台，可直接拍下。

17基于matlab卡尔曼滤波的行人跟踪算法，并给出算法估计误差结果，判断算法的跟踪精确性，程序已调通，可直接运行，基于MATLAB平台，可直接拍下。 17matlab卡尔曼滤波行人跟踪 (xiaohongshu.com)...

编程日记 2023/10/11 6:04:50

SpringCloud之Stream框架集成RocketMQ消息中间件

Spring Cloud Stream 是一个用来为微服务应用构建消息驱动能力的框架。它可以基于 Spring Boot 来创建独立的、可用于生产的 Spring 应用程序。Spring Cloud Stream 为一些供应商的消息中间件产品提供了个性化的自动化配置实现，并引入了发布-订阅、消费组、分区这三…...

编程日记 2023/10/11 6:03:46

与创新者同行！Apache Doris 首届线下峰会即将开启，最新议程公开！｜即刻预约

点击此处 即刻报名 Doris Summit Asia 2023 回顾人类的发展史，地球起源于 46 亿年前的原始星云、地球生命最初出现于 35 亿年前的原始海洋、人类物种诞生于数百万年前，而人类生产力的真正提升源于十八世纪六十年代的工业革命，自此以后&#…...

编程日记 2023/10/11 6:02:44

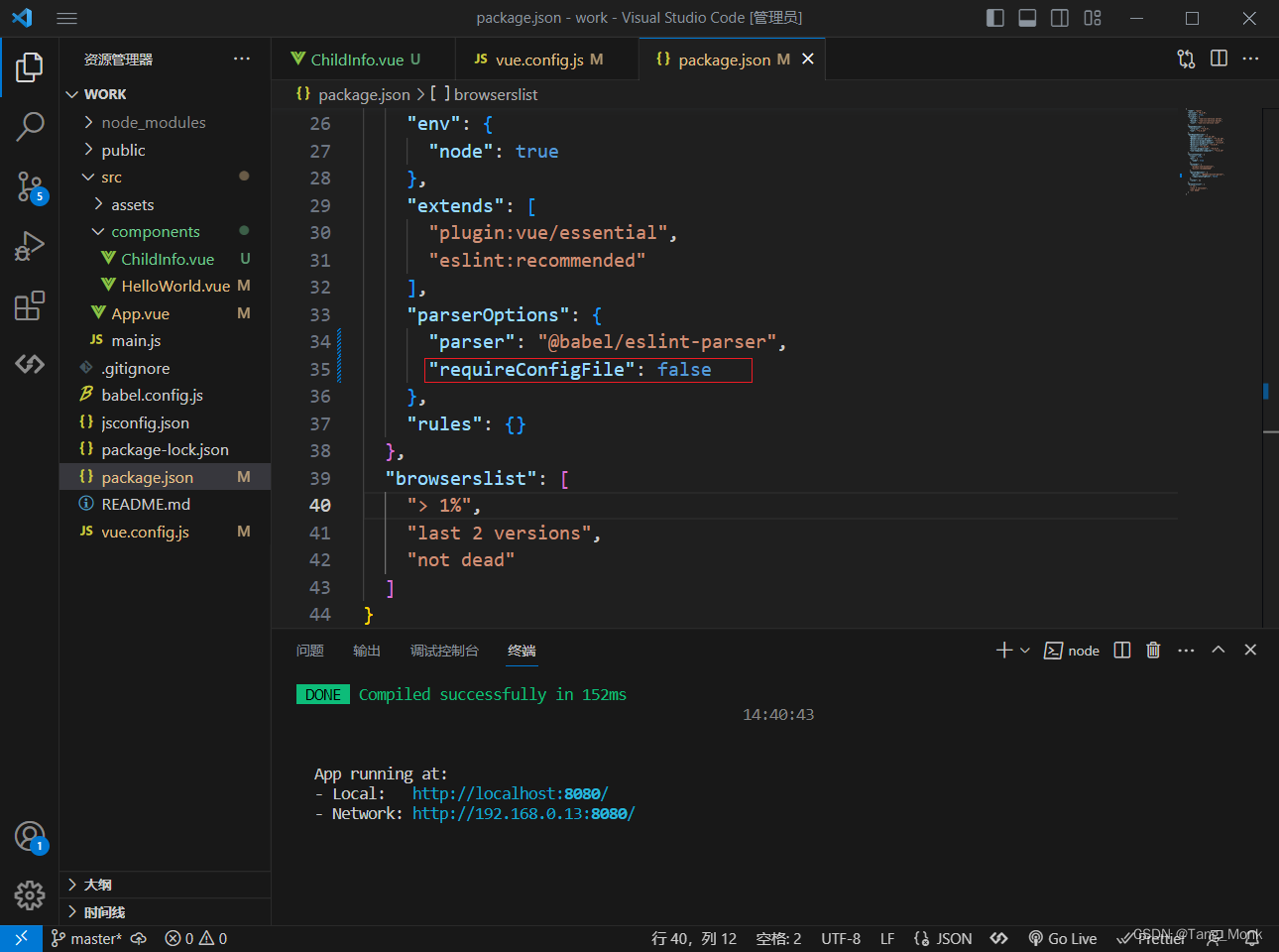
vue解决：Parsing error: No Babel config file detected for ....

报错信息 Parsing error: No Babel config file detected for C:\Users\Admin\Desktop\shabi\work\src\App.vue. Either disable config file checking with requireConfigFile: false, or configure Babel so that it can find the config files. 分析错误：没有检测…...

编程日记 2023/10/11 6:01:43

算法题：K 次取反后最大化的数组和（典型的贪心算法问题）

这道题没有看题解，直接提交，成绩超越99.5%，说明思路是优的。就是考虑的情况里面弯弯绕比较多，需要考虑全面一点。（本题完整题目附在了最后面） 具体思路如下： 1、首先排序，然后从最…...

编程日记 2023/10/11 6:00:42

Go语言中向[]byte数组中增加一个元素

要向http.Request的body中添加一个键值对，可以先将其转换为一个map，然后对其进行修改，最后再将其转回为byte数组。 以下是一个示例代码： import ("net/http""io/ioutil""encoding/json" )type Re…...

编程日记 2023/10/11 5:59:40

CSS 布局案例： 2行、多行每行格数不定，最后一列对齐

布局期望的效果如下&#xff1a; 第二行最后一格与第一行最后一格对齐。每行格数不定。自动拉伸填充整个宽度 实现&#xff1a; 一开始打算用display:flex&#xff0c; 自动分散&#xff0c;但是第二行对齐第一行最后一格控制不了。 使用grid fr均分单位控制。 <!DOCTYPE…...

编程日记 2023/10/11 5:57:35

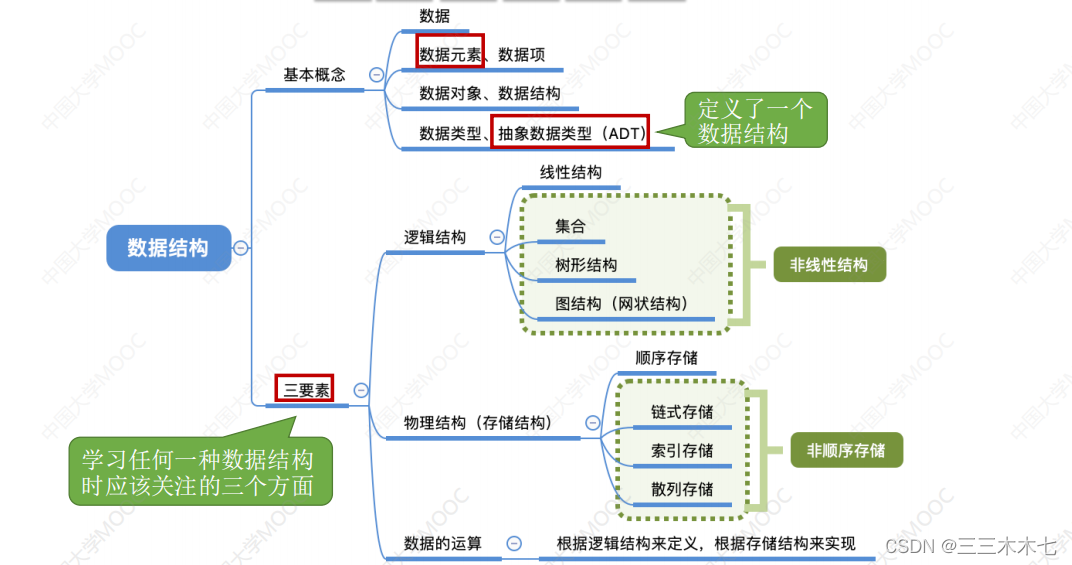
数据结构--算法、数据结构的基本概念

&#x1f4d5;参考&#xff1a;王道 一、算法的基本概念 1.程序数据结构算法 2.算法的特性 &#xff08;1&#xff09;有穷性 执行有穷步之后结束&#xff0c;且每一步都可在有穷时间内完成。 &#xff08;2&#xff09;确定性 &#xff08;3&#xff09;可行性 可通过已经实…...

编程日记 2023/10/11 5:56:32

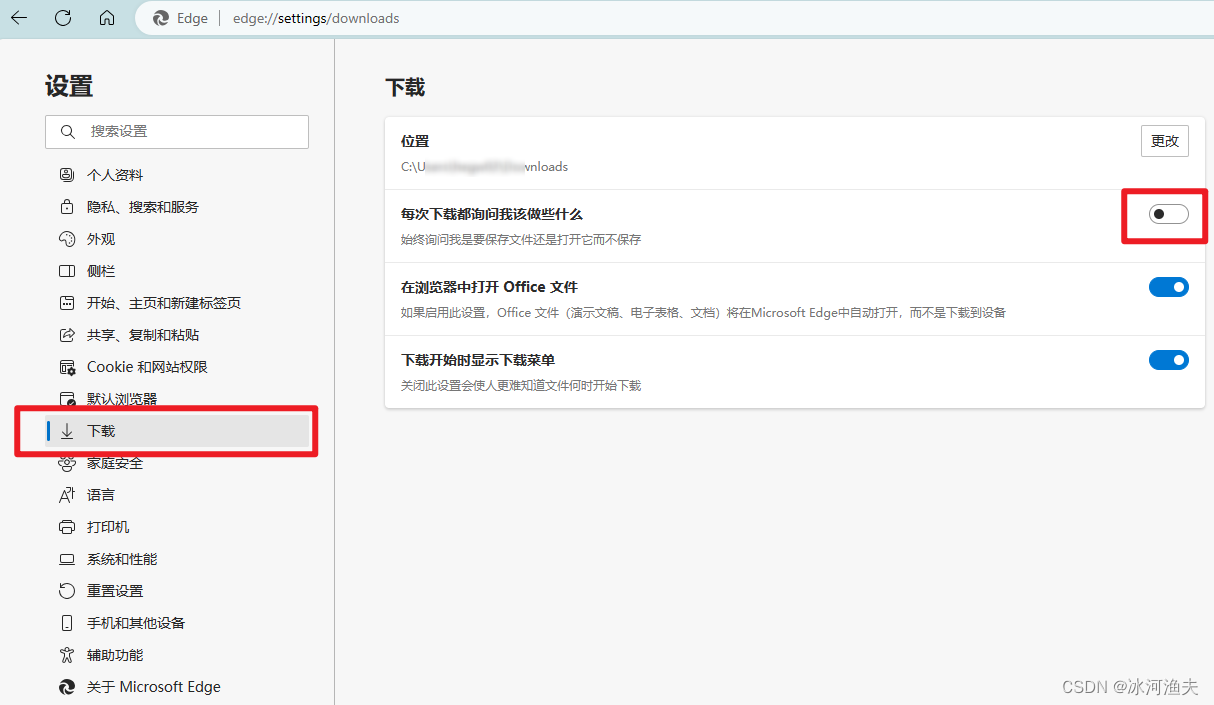
Edge浏览器下载文件被保存为 .crdownload 文件的问题小记

问题 近期使用Edge浏览器下载文件时&#xff0c;文件都被保存为 .crdownload 格式的文件了&#xff0c;不确定从哪个版本开始的。除非下载未完成导致文件不完整&#xff0c;否则不会被保存为 .crdownload 格式的文件&#xff1b;实际上文件已完成了下载&#xff0c;且手工修改…...

编程日记 2023/10/11 5:55:31

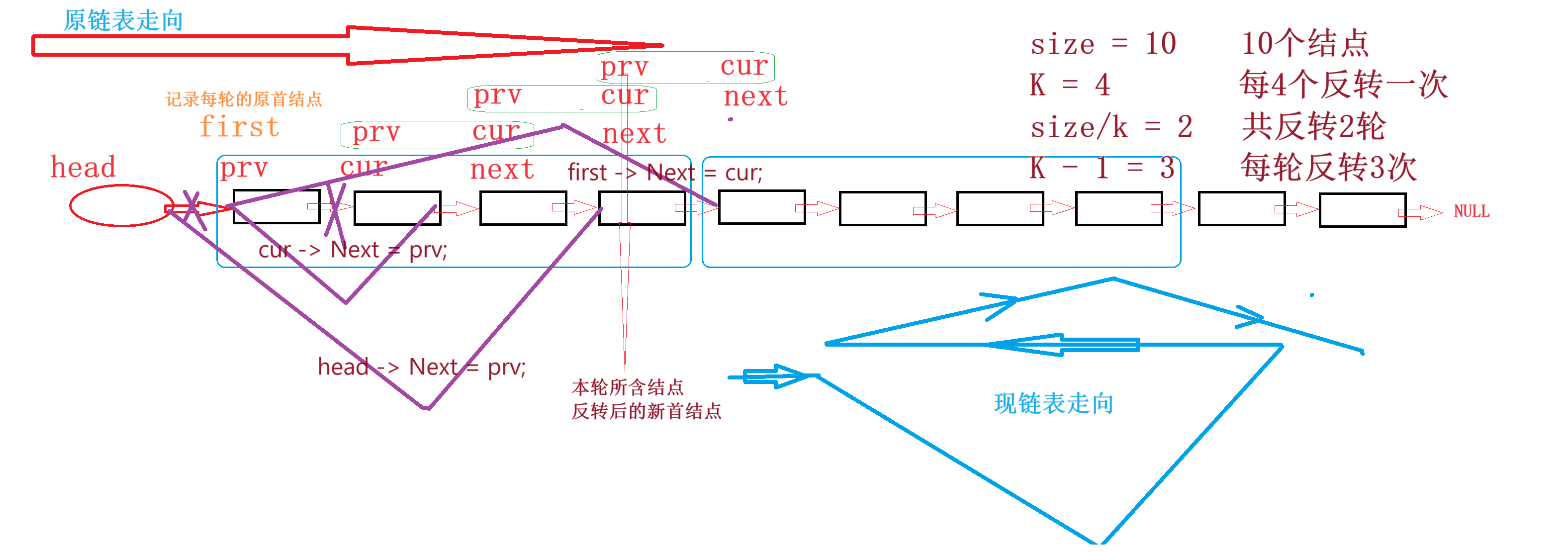
6-10 单链表分段逆转 分数 15

void K_Reverse( List L, int K ) { //此题已经默认size > K 因为当size < K时 反转后将不再符合链表的定义//求出表中元素个数int size 0;for (List cur L->Next; cur ! NULL; cur cur->Next)size; List prv, cur, next, first, head L;//共需要反转 si…...

编程日记 2023/10/11 5:54:30

【单片机】17-温度传感器DS18B20

1.DS18B20相关背景知识 1.温度传感器 &#xff08;1&#xff09;测温度的方式&#xff1a;物理&#xff08;汞柱&#xff0c;气压&#xff09;&#xff0c;电子&#xff08;金属电性能随温度变化&#xff09; &#xff08;2&#xff09;早期&#xff1a;热敏电阻&#xff08;模…...

编程日记 2023/10/11 5:53:28

力扣 -- 5. 最长回文子串

解题步骤&#xff1a; 参考代码&#xff1a; class Solution { public:string longestPalindrome(string s) {int ns.size();vector<vector<bool>> dp(n,vector<bool>(n));//最长回文串的起始位置int start0;//最长回文串的长度int len0;for(int in-1;i>…...

编程日记 2023/10/11 5:50:25

SpringCloud源码探析（十）-Web消息推送

1.概述 消息推送在日常使用中的场景比较多&#xff0c;比如有人点赞了我的博客或者关注了我&#xff0c;这时我就会收到一条推送消息&#xff0c;以此来吸引我点击或者打开应用。消息推送的方式主要分为两种&#xff1a;web消息推送和移动端消息推送。它将所要发送的信息&…...

编程日记 2023/10/11 5:49:23

Vue、React和小程序中的组件通信：父传子和子传父

在前端开发中&#xff0c;组件化是一种常见的开发模式&#xff0c;它可以将复杂的用户界面拆分成多个可重用的组件。在Vue、React和小程序中&#xff0c;组件之间的数据和事件传递是非常关键的&#xff0c;其中父传子和子传父是常见的通信方式。本文将介绍在Vue、React和小程序…...

编程日记 2023/10/11 5:47:21

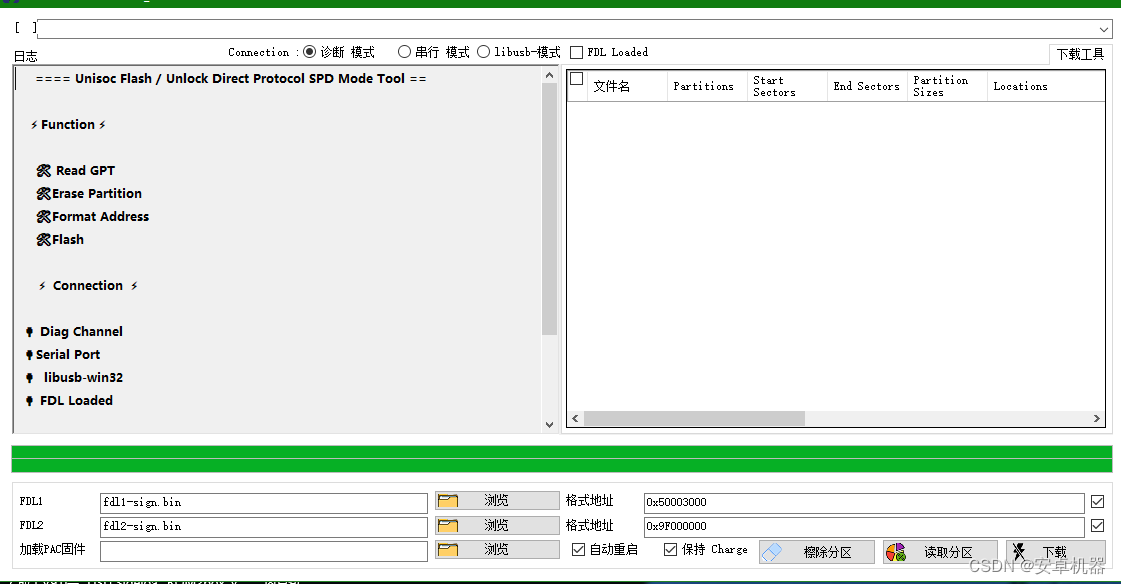
安卓玩机----展讯芯片机型解锁 读写分区工具 操作步骤解析

国内机型大都使用高通和MTK芯片。展讯芯片使用的较少。相对来说高通和mtk机型解锁以及读取分区工具较多。展讯的几乎没有。目前有大佬开发出了一款展讯芯片解锁 与读写分区工具.开源的tools 官方分享说明&#xff1a; 是一款专为 Windows 计算机设计的免费、用户友好的工具&am…...

编程日记 2023/10/11 5:46:20

微软放大招！Bing支持DALL-E3，免费AI绘画等你来体验！

最近 OpenAI 发布了DALL-E3模型&#xff0c;出图效果和Midjourney不相上下&#xff0c;不过要使用它有些门槛&#xff0c;必须是 ChatGPT Plus 账户&#xff0c;而且还要排队&#xff0c;怎么等都等不到&#xff0c;搞得大家都比较焦虑。 不过现在微软在Bing上也支持 DALL-E3 …...

编程日记 2023/10/11 5:45:19

tp5访问的时候必须加index.php,TP5配置隐藏入口index.php文件

PS&#xff1a;这里说的入口文件指的是public/index.php,配置文件就在这个目录下 可以去掉URL地址里面的入口文件index.php&#xff0c;但是需要额外配置WEB服务器的重写规则。 以Apache为例&#xff0c;需要在入口文件的同级添加.htaccess文件(官方默认自带了该文件)&#x…...

编程日记 2023/10/11 5:42:16

16k面试中的10个问题

你好&#xff0c;我是田哥 节前&#xff0c;有位朋友跟我反馈面试中一些问题&#xff0c;这位朋友的基本情况&#xff1a; 坐标&#xff1a;上海&#xff0c;年限&#xff1a;3年不到&#xff0c;期望薪资&#xff1b;16k 下面我们来看看具体问题&#xff1a; 01&#xff1a;请…...

编程日记 2023/10/11 5:41:15

STM32单片机入门学习（六）-光敏传感器控制LED

光敏传感器模块和LED接线 LED负极接B12,正极接VCC 光敏传感模块一DO端接B13,GND接GND&#xff0c;VCC接VCC,AO不接。 如图&#xff1a; 主程序代码&#xff1a;main.c #include "stm32f10x.h" #include "Delay.h" //delay函数所在头文件 #include …...

编程日记 2023/10/11 5:40:14

MFC 鼠标悬停提示框

MFC 鼠标悬停提示框 运行效果 在MFC窗口中添加一个控件 工具栏中拖拽List Box到MFC窗口给List Box添加变量 CListBox m_listbox 增加成员变量 CWnd* m_tip_parent_wnd; CToolTipCtrl m_tip;给m_listbox创建提示框 void create_tip_window(CWnd* tip_wnd, CToolTipCtrl* ti…...

编程日记 2023/10/11 5:39:12

大数据学习，涉及哪些技术？

学习大数据需要涉及多种技术和概念&#xff0c;因为大数据领域非常广泛&#xff0c;涵盖了数据的采集、存储、处理、分析和可视化等多个方面。以下是学习大数据时需要考虑的一些关键技术和概念&#xff1a; 1、数据采集和存储&#xff1a; 数据库管理系统&#xff08;DBMS&am…...

编程日记 2023/10/11 5:38:11

Clion中使用C/C++开发stm32程序

前言 从刚开始学习阶段&#xff0c;一直是用的keil5开发stm32程序&#xff0c;自从看到稚晖君推荐的CLion开发嵌入式程序后&#xff0c;这次尝试在CLion上开发stm32程序。 1、配置CLion用于STM32开发的环境 这里我就不详细写了&#xff0c;没必要重新写&#xff0c;网上教程很多…...

编程日记 2023/10/11 5:37:08

JavaScript Web APIs第五天笔记

Web APIs - 第5天笔记 目标&#xff1a; 能够利用JS操作浏览器,具备利用本地存储实现学生就业表的能力 BOM操作综合案例 js组成 JavaScript的组成 ECMAScript: 规定了js基础语法核心知识。比如&#xff1a;变量、分支语句、循环语句、对象等等 Web APIs : DOM 文档对象模型&…...

编程日记 2023/10/11 5:35:06

[ICCV-23] Paper List - 3D Generation-related

ICCV-23 paper list 目录 Oral Papers 3D from multi-view and sensors Generative AI Poster Papers 3D Generation (Neural generative models) 3D from a single image and shape-from-x 3D Editing Face and gestures Stylization Dataset Oral Papers 3D from …...

编程日记 2023/10/11 5:34:05

Transformer为什么如此有效 | 通用建模能力，并行

目录 1 更强更通用的建模能力 2 并行计算 3 大规模训练数据 4 多训练技巧的集成 Transformer是一种基于自注意力机制的网络&#xff0c;在最近一两年年可谓是大放异彩&#xff0c;我23年入坑CV的时候&#xff0c;我看到的CV工作似乎还没有一个不用到Transformer里的一些组…...

编程日记 2023/10/11 5:33:02

【初识Jmeter】【接口自动化】

jmeter的使用笔记1 Jmeter介绍与下载安装介绍安装配置配置与扩展组件 jmeter的使用基本功能元素登陆请求与提取cookie其他请求接口关联Cookie-响应成功聚合报告查看 Jmeter介绍与下载安装 介绍 jmeter是apache公司基于java开发的一款开源压力测试工具&#xff0c;体积小&…...

编程日记 2023/10/11 5:32:01

C:数组传值调用和传地址调用

传地址调用 对数组进行修改&#xff1a;排序… #include <stdio.h>// 函数用于交换两个整数的值 void swap(int *a, int *b) {int temp *a;*a *b;*b temp; }// 函数用于对整数数组进行升序排序 void sortArray(int *arr, int size) {for (int i 0; i < size - 1…...

编程日记 2023/10/11 5:30:59