算法-DFS+记忆化/动态规划-不同路径 II
算法-DFS+记忆化/动态规划-不同路径 II
1 题目概述
1.1 题目出处
https://leetcode.cn/problems/unique-paths-ii
1.2 题目描述
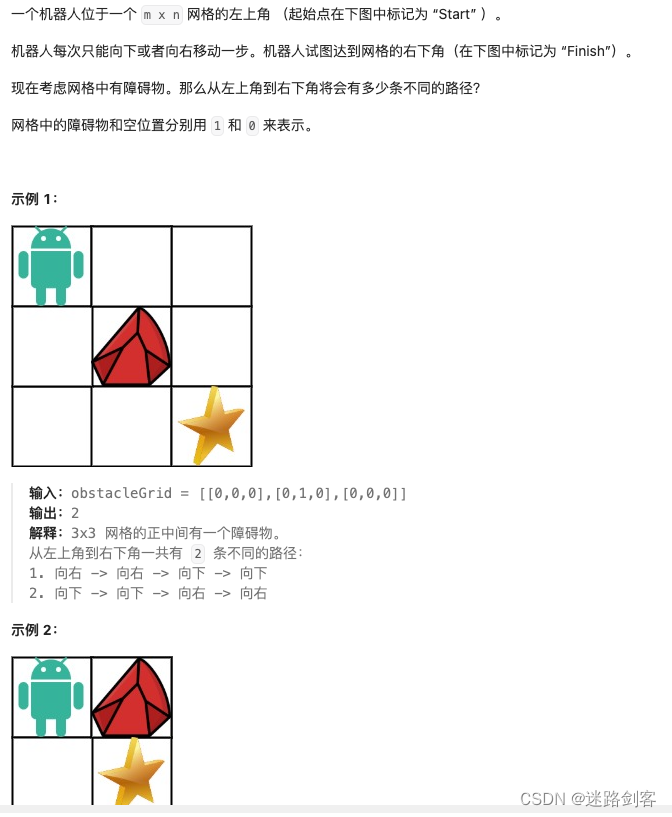

2 DFS+记忆化
2.1 思路
注意题意,每次要么往右,要么往下走,也就是说不能走回头路。但是仍有可能走到之前已经访问过的节点。题意是要求走到终点的路径数,假设往右可以走通,往下也可以走通,那么当前格子的走通方法数 = 往右走通方法数 + 往下走通方法数。
2.2 代码
class Solution {int m = 0;int n = 0;int[][] paths = null;public int uniquePathsWithObstacles(int[][] obstacleGrid) {m = obstacleGrid.length;n = obstacleGrid[0].length;paths = new int[m][n];return dfs(obstacleGrid, 0, 0);} private int dfs(int[][] obstacleGrid, int i, int j) {if (paths[i][j] > 0) {return paths[i][j];}if (obstacleGrid[i][j] == 1) {return 0;}if (i == m - 1 && j == n - 1) {paths[i][j] = 1;return 1;}int result = 0;if (i < m - 1) {result += dfs(obstacleGrid, i + 1, j);}if (j < n - 1) {result += dfs(obstacleGrid, i, j + 1);}paths[i][j] = result;return result;}
}
2.3 时间复杂度
O(m*n)

2.4 空间复杂度
O(m*n)
3 二维动态规划
3.1 思路
从上述DFS中思考,可以推出动态规划表达式:dp[i][j] = dp[i+1][j] + dp[i][j+1]。
这里注意两点:
- dp[m-1][n-1] 的值,需要看obstacleGrid[m-1][n-1]是否为1,如果为1代表是障碍,则直接就返回0了。否则就填为1.
- 从动态规划表达式可知,需要i和j都从大到小遍历才可计算。
3.2 代码
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;if (n == 0) {return 1;}if (obstacleGrid[m - 1][n - 1] == 1) {return 0;}// dp[i][j] = dp[i+1][j] + dp[i][j+1]int[][] dp = new int[m][n];dp[m-1][n-1] = 1;for (int i = m - 1; i >= 0; i--) {for (int j = n - 1; j >= 0; j--) {if (obstacleGrid[i][j] == 1) {dp[i][j] = 0;continue;}if (i < m - 1) {dp[i][j] = dp[i+1][j];}if (j < n - 1) {dp[i][j] += dp[i][j+1];}}}return dp[0][0];}
}
3.3 时间复杂度
O(M*N)
3.4 空间复杂度
O(M*N)
4 一维动态规划
4.1 思路
尝试压缩为一维动态规划。
- 考虑dp[i][j] = dp[i+1][j] + dp[i][j+1],那么如果我们每次固定i值,从最后一行的j从大到小递减计算,就能计算出最后一行的各个dp[j]值。
- 然后i-1到上一行,此时,dp[j]依然表示此行每个位置的通终点方法数,相当于是已经从当前位置累加了往下走的路线的方法数,即
dp[i][j] = dp[i+1][j] + dp[i][j+1]中的dp[i+1][j],那么我们只需要再计算本行的dp[i][j+1]即可。 - 综上所述,我们可以压缩二维动态规划为一维动态规划:
dp[j] += dp[j+1]
4.2 代码
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;if (n == 0) {return 1;}if (obstacleGrid[m - 1][n - 1] == 1) {return 0;}int[] dp = new int[n];dp[n-1] = 1;for (int i = m - 1; i >= 0; i--) {for (int j = n - 1; j >= 0; j--) {if (obstacleGrid[i][j] == 1) {dp[j] = 0;continue;}if (j < n - 1) {dp[j] += dp[j+1];}}}return dp[0];}
}
4.3 时间复杂度
3.4 空间复杂度
O(N)
相关文章:

算法-DFS+记忆化/动态规划-不同路径 II
算法-DFS记忆化/动态规划-不同路径 II 1 题目概述 1.1 题目出处 https://leetcode.cn/problems/unique-paths-ii 1.2 题目描述 2 DFS记忆化 2.1 思路 注意题意,每次要么往右,要么往下走,也就是说不能走回头路。但是仍有可能走到之前已经…...
黑盒测试方法:原理+实战
目录 一、如何设计测试用例 二、黑盒测试常用方法 1、基于需求进行测试用例的设计 2、等价类 3、边界值 4、判定表分析法(因果分析法) 5、正交表 6、场景设计法 三、案例补充 1、使用Fiddler模拟弱网 2、针对一个接口该如何测试 一、如何设计测试…...

SQLite事务处理
语法 BEGIN TRANSACTION; COMMIT TRANSACTION; (或END TRANSACTION;) ROLLBACK TRANSACTION; 事务处理 除了一些PRAGMA语句以外,其它访问数据库的语句会自动启动事务处理,并且在结束时自动提交。 通过上一节的命令可以手动控制…...

Java中CountDownLatch使用场景
在Java的并发API中,CountDownLatch是一个同步器,它允许一个或多个线程等待一组操作完成。 如果您正在开发一个服务器应用程序,该应用程序在开始处理请求之前需要初始化各种资源。这些资源可能是这样的: 加载配置文件建立数据库连…...
漏刻有时数据可视化Echarts组件开发(41)svg格式地图应用
1.定义SVG文件 var svg ;2.注册地图函数 Echarts.registerMap是Echarts图表库中用于注册地图的函数。它可以将第三方地图或自定义地图数据与Echarts进行集成,使用Echarts的API进行绘制。使用方法如下: echarts.registerMap(mapName, geoJson) 参数map…...

firefox的主题文件位置在哪?记录以防遗忘
这篇文章写点轻松的 最近找到了一个自己喜欢的firefox主题,很想把主题的背景图片找到,所以找了下主题文件所在位置 我的firefox版本:版本: 118.0.1 (64 位)主题名称: Sora Kawai 我的位置在 C:\Users\mizuhokaga\AppData\Roaming\Mozilla\Firefox\Profiles\w0e4e24v.default…...
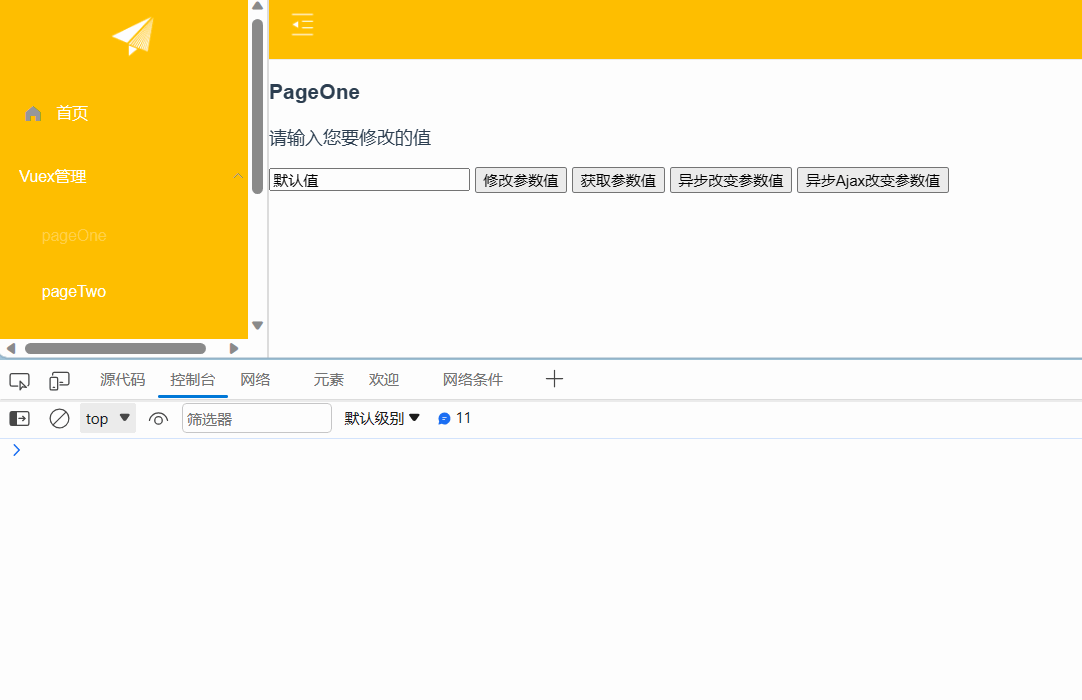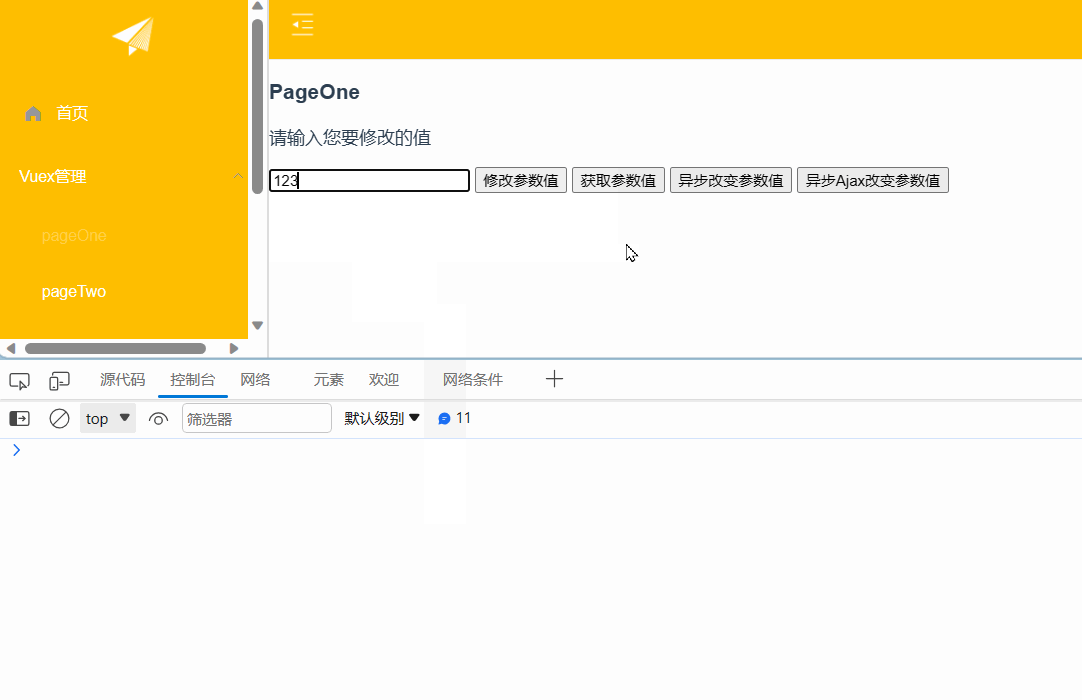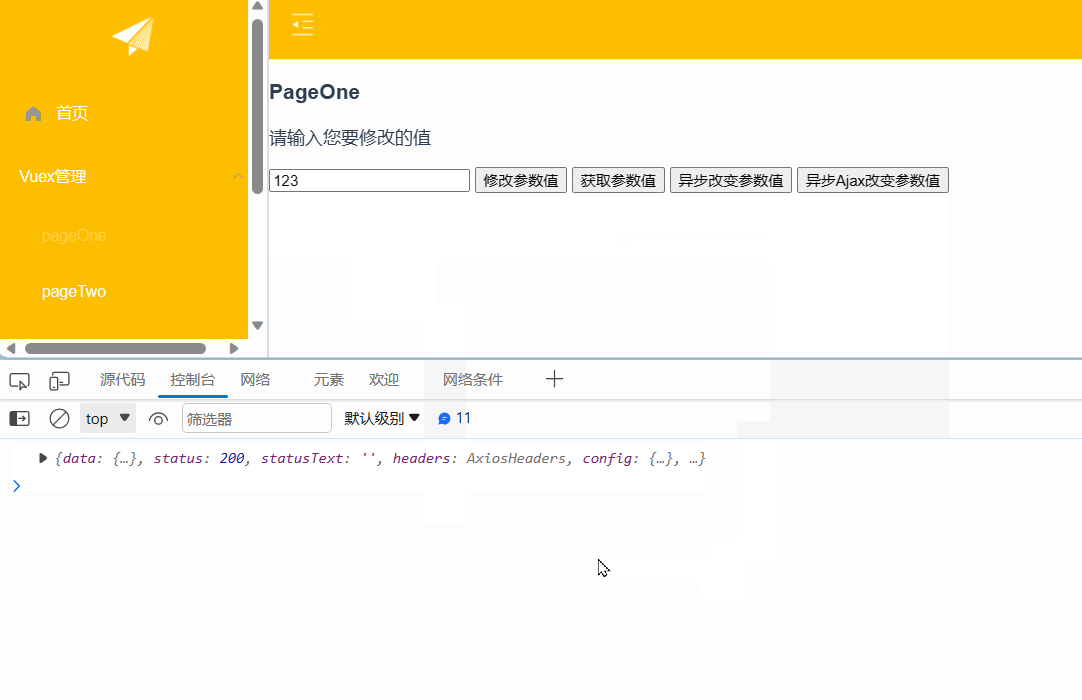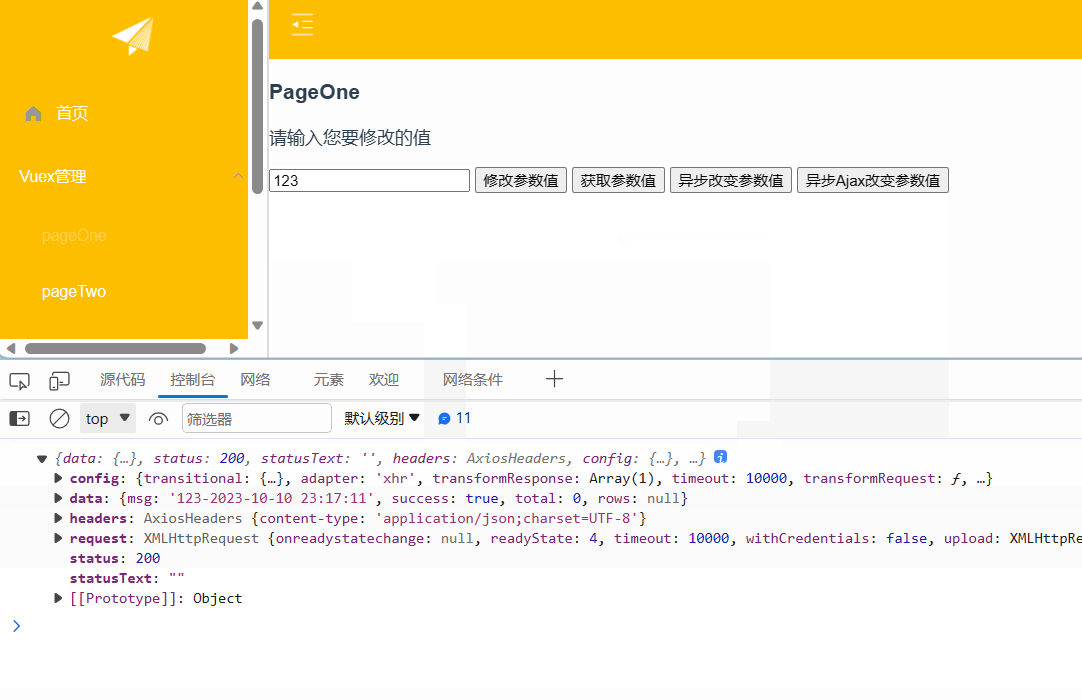
Vuex获取、修改参数值及异步数据处理
14天阅读挑战赛 学不可以已... 目录 一、Vuex简介 1.1 vuex介绍 1.2 vuex核心 二、Vuex使用 2.1 Vuex安装 2.2 创建store模块 2.3 创建vuex的store实例并注册上面引入的各大模块 三、使用Vuex获取、修改值案例 3.1 创建两个菜单组件 3.2 配置路由 3.3 模拟菜单数据 …...
(二)】)
【 OpenGauss源码学习 —— 列存储(autoanalyze)(二)】
列存储(autoanalyze)(二) 概述PgStat_StatTabEntry 结构体pgstat_count_heap_insert 与 pgstat_count_cu_insert 函数CStoreInsert::BatchInsertCommon 函数pgstat_count_cu_update 函数pgstat_count_cu_delete 函数pgstat_count_…...

使用postman 调用 Webservice 接口
1. 先在浏览器地址栏 访问你的webService地址 地址格式: http://127.0.0.1:8092/xxxx/ws(这个自己的决定)/xxxxXccv?wsdl 2. post man POST 访问wwebService接口 地址格式: http://127.0.0.1:8092/xxxx/ws(这个自己的决定)/xxxxXccv <soapenv:Envelope xmlns:soapenv…...

程序员Google插件推荐
文章目录 AdBlock (广告拦截插件)SuperCopy 超级复制Octotree (github增强工具)GitZip for github (github增强工具)JSON-handleSimpleExtManager(管理谷歌插件)OneTab (标签页合并)PostWoman(接口调试)篡改猴 (Tampermonkey)FeHelper(前端助手) AdBlock (广告拦截插件) ☆ 拦截…...

机器学习中常见的监督学习方法和非监督学习方法有哪些。
问题描述:最近面试某些公司算法岗,看到一道简答题,让你举例熟悉的监督学习方法和非监督学习方法。 问题解答: 监督学习方法常见的比较多: 线性回归(Linear Regression): 用于回归问…...

UEFI基础——测试用例Hello Word
Hello 测试用例 硬件环境:龙芯ls3a6000平台 软件环境:龙芯uefi固件 GUID获取网址:https://guidgen.com 一、创建工程 mkdir TextPkg/三个文件 Hello.c 、 Hello.inf 、HelloPkg.dsc 1.1 Hello.c /** fileThe application to print hello …...
【tomcat、java】
java:maven配置 1.安装插件 <build><plugins><plugin><groupId>org.apache.tomcat.maven</groupId><artifactId>tomcat7-maven-plugin</artifactId><version>2.1</version><configuration><port&…...

京东获取推荐商品列表 API
item_recommend-获取推荐商品列表 请求参数 请求参数:type 参数说明:type:推荐类型 进入API测试页 响应参数 Version: Date: 名称类型必须示例值描述 items items[]0获取推荐商品列表 num_iid Bigint010021415166448宝贝ID detail_url String0http…...
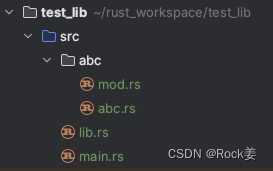
rust cfg的使用
前提是一个crate倒入另一个crate。 先看结构 test_lib目录结构 这与另一个crate处于同一个目录,所以另一crate倒入的时候在Cargo.toml中使用如下语句。 test_lib = {path = "../test_lib" }先在test_lib/src/abc/abc.rs中添加没有cfg的两个函数做测试。 pub fn…...

电脑屏幕怎么录制?5 个最佳免费录屏软件
您是否想使用网络摄像头录制优酷视频、抖音直播或在线课程等项目,但完全不知道如何开始? 不用担心。有很多软件选项可以帮助您。虽然每一款都有不同的功能,但它们都能够录制网络摄像头并输出精美的高质量视频。 以下是我们精选的最佳作品。…...
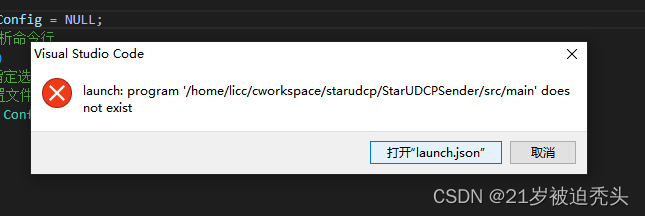
vscode 调试使用 make 编译的项目
1、首先点击运行 --> 启动调试: 2、选择g或gcc生成和调试活动文件: 3、出现下面提示是正常的,点击仍要调试: 点击打开“launch.json”: 4、此时会在项目工作目录下生成tsak.josn和launch.json文件: 如…...
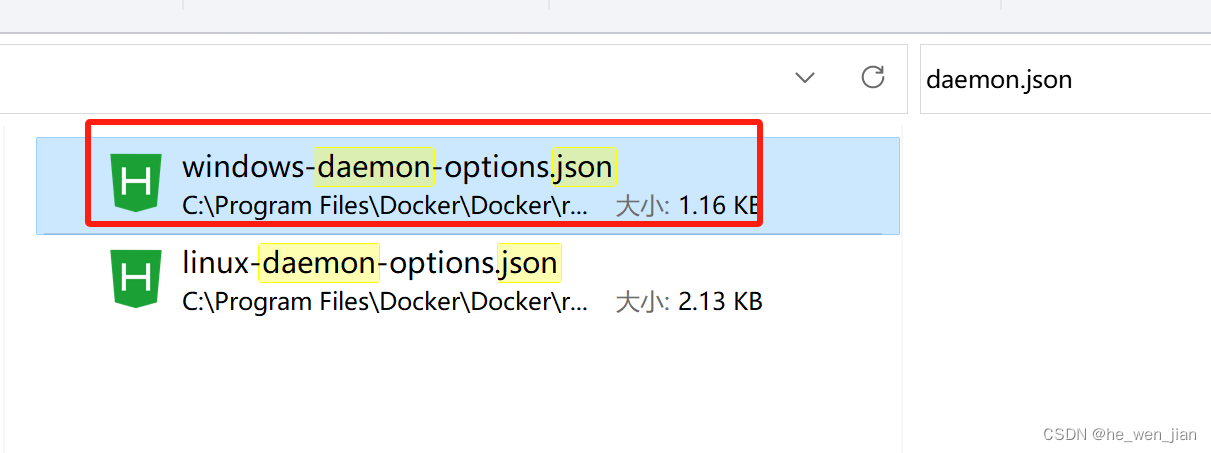
Docker修改阿里源
在一次安装rtmp推流服务时,总是无法下载源,估计是国外资源下载超时照成的,于是想到修改为国内源。 docker pull alfg/nginx-rtmp Using default tag: latest latest: Pulling from alfg/nginx-rtmp 530afca65e2e: Retrying in 7 seconds c20…...

有必要买一台内衣裤专洗机吗?家用小洗衣机推荐
随着内衣洗衣机的流行,很多小伙伴在纠结该不该入手一款内衣洗衣机,专门来洗一些贴身衣物,答案是非常有必要的,因为我们现在市面上的大型洗衣机只能做清洁,无法对我们的贴身衣物进行一个高强度的清洁,而小小…...
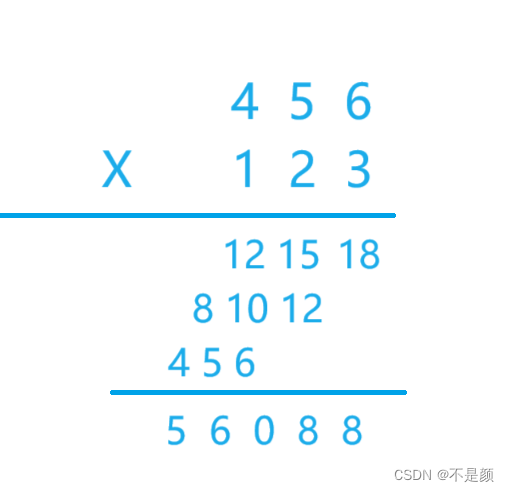
高精度与高精度的乘法---基础算法
看到一个博主写得不错,我也照猫画虎:) 原因 在计算两个非负整数时,如果位数很大,连 long long 类型都存储不了,就要使用到高精度的乘法 原理 原理依旧是模拟人计算两个数的积,早在小学我们已…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...

接口 RESTful 中的超媒体:REST 架构的灵魂驱动
在 RESTful 架构中,** 超媒体(Hypermedia)** 是一个核心概念,它体现了 REST 的 “表述性状态转移(Representational State Transfer)” 的本质,也是区分 “真 RESTful API” 与 “伪 RESTful AP…...
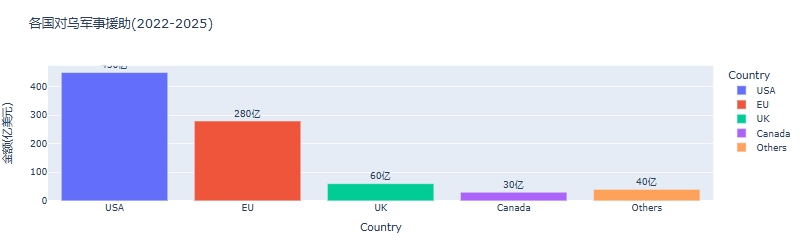
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...

break 语句和 continue 语句
break语句和continue语句都具有跳转作用,可以让代码不按既有的顺序执行 break break语句用于跳出代码块或循环 1 2 3 4 5 6 for (var i 0; i < 5; i) { if (i 3){ break; } console.log(i); } continue continue语句用于立即终…...
