【数据结构】二叉树--堆排序
目录
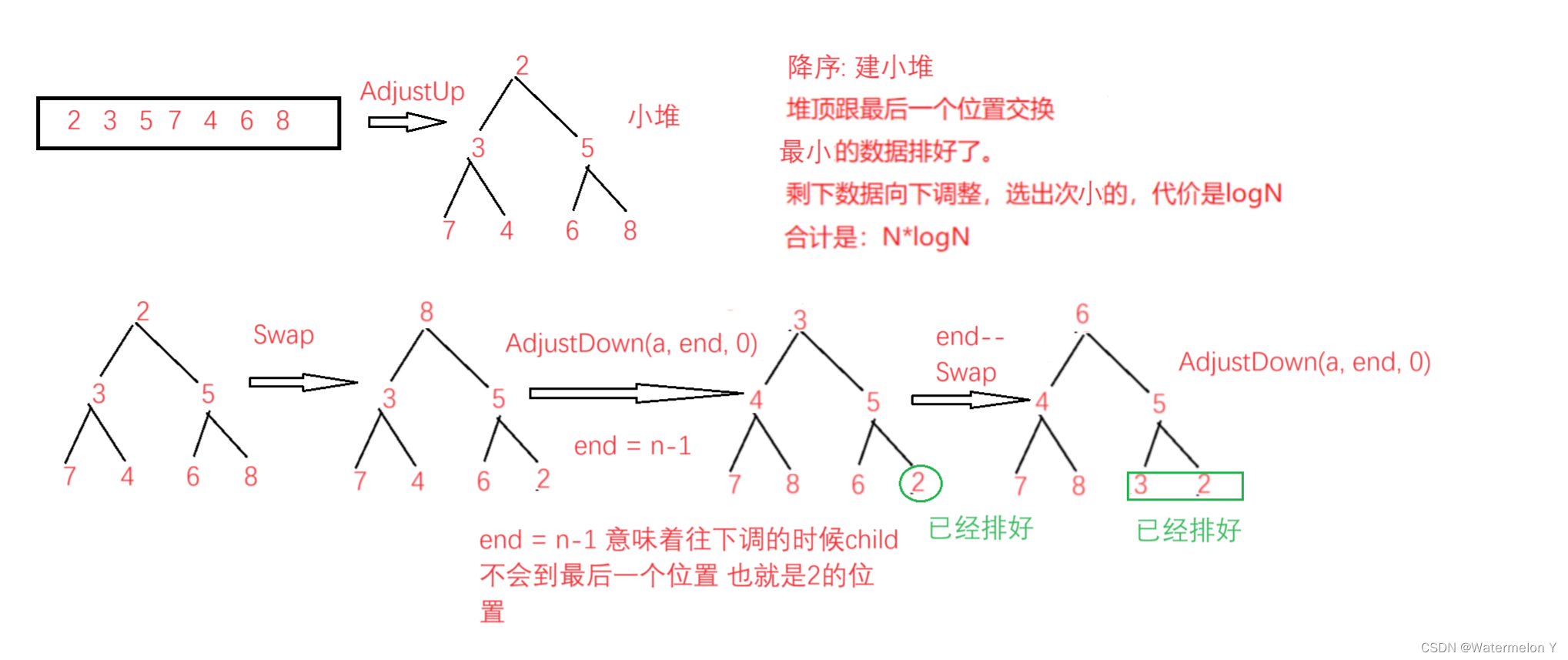
一 降序(建小堆)
二 升序 (建大堆)
三 优化(以升序为例)
四 TOP-K问题
一 降序(建小堆)
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}//降序 建小堆
void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{int end = n - 1;int i = 0;//建堆for (i = 1; i < n; i++){AdjustUp(a, i);}while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}int main()
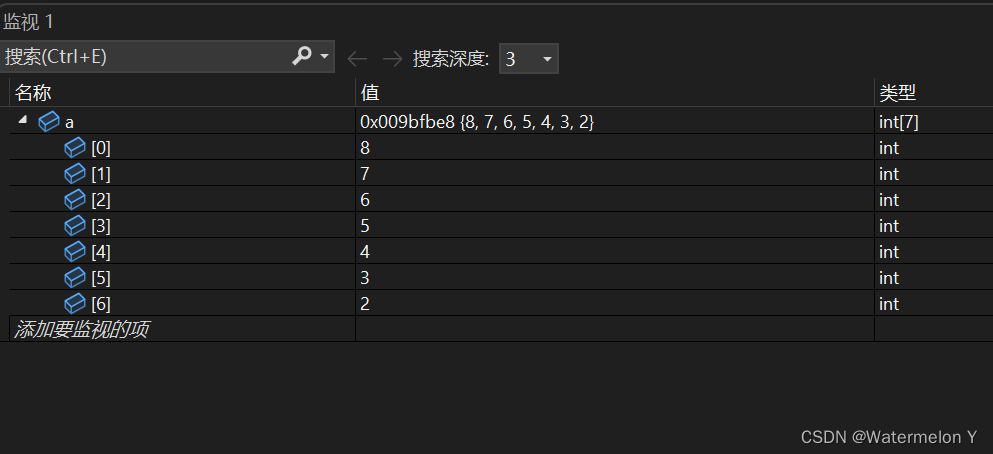
{int a[] = { 2, 3, 5, 7, 4, 6, 8 };HeapSort(a, sizeof(a) / sizeof(int));return 0;
}
二 升序 (建大堆)
//升序 建大堆
void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{int end = n - 1;int i = 0;//建堆for (i = 1; i < n; i++){AdjustUp(a, i);}while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}int main()
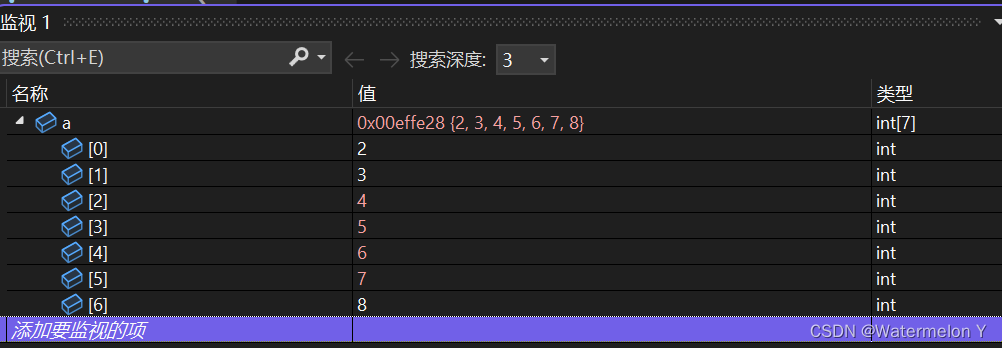
{int a[] = { 2, 3, 5, 7, 4, 6, 8 };HeapSort(a, sizeof(a) / sizeof(int));return 0;
}
三 优化(以升序为例)
可以用向下建堆的方法
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//void HeapSort(int* a, int n)
//{
// int end = n - 1;
// int i = 0;
// //建堆
// for (i = 0; i < n; i++)
// {
// AdjustUp(a, i);
// }
//
// while (end > 0)
// {
// Swap(&a[0], &a[end]);
// AdjustDown(a, end, 0);
// end--;
// }
//}void HeapSort(int* a, int n)
{int end = n - 1;int i = 0;//建大堆for (i = (n-1-1) / 2; i >= 0; i--){AdjustDown(a, n, i);}while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
int main()
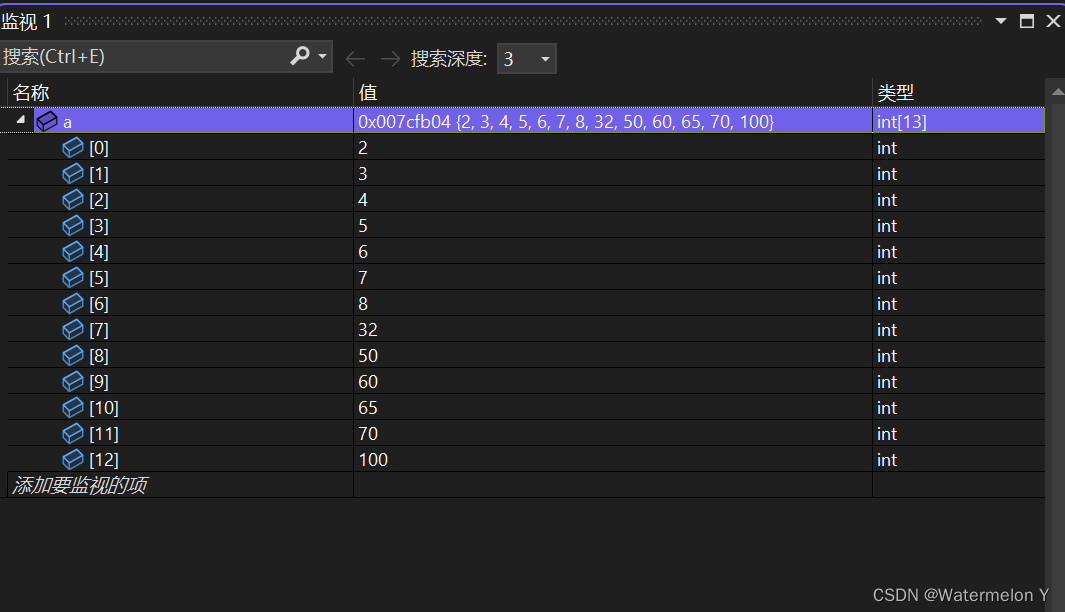
{int a[] = { 2, 3, 5, 7, 4, 6, 8, 65, 100, 70, 32, 50, 60};HeapSort(a, sizeof(a) / sizeof(int));return 0;
}
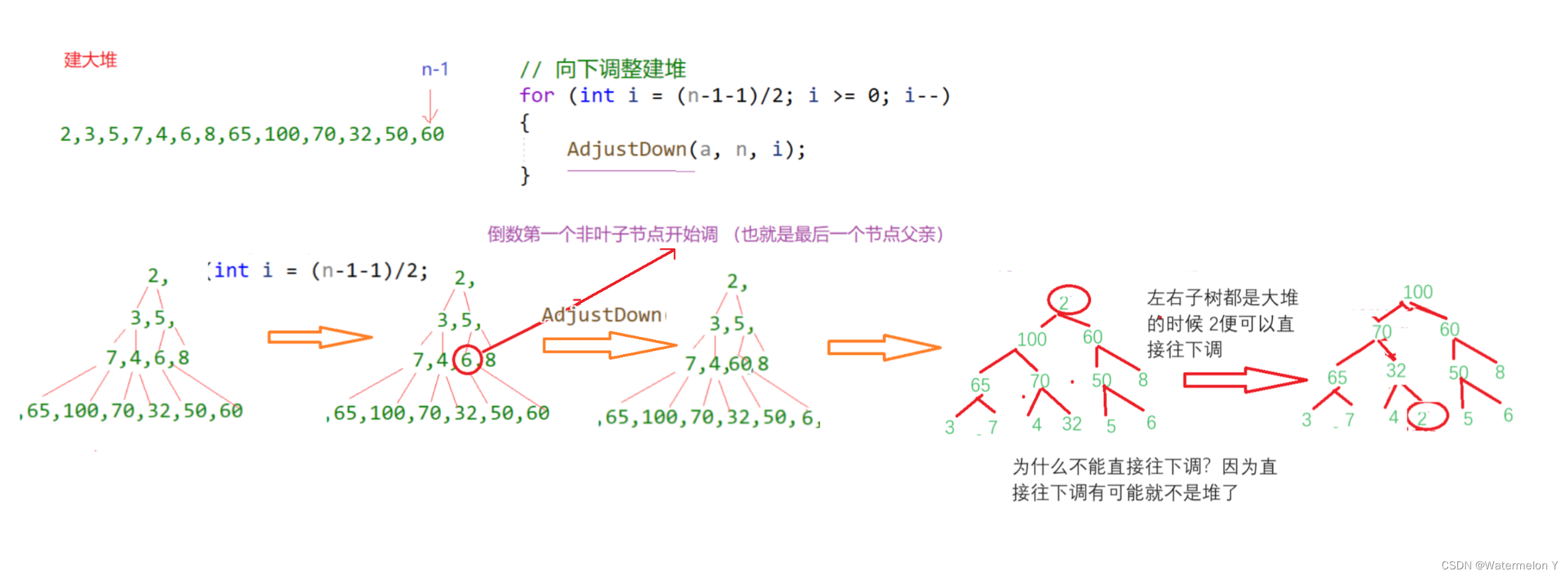
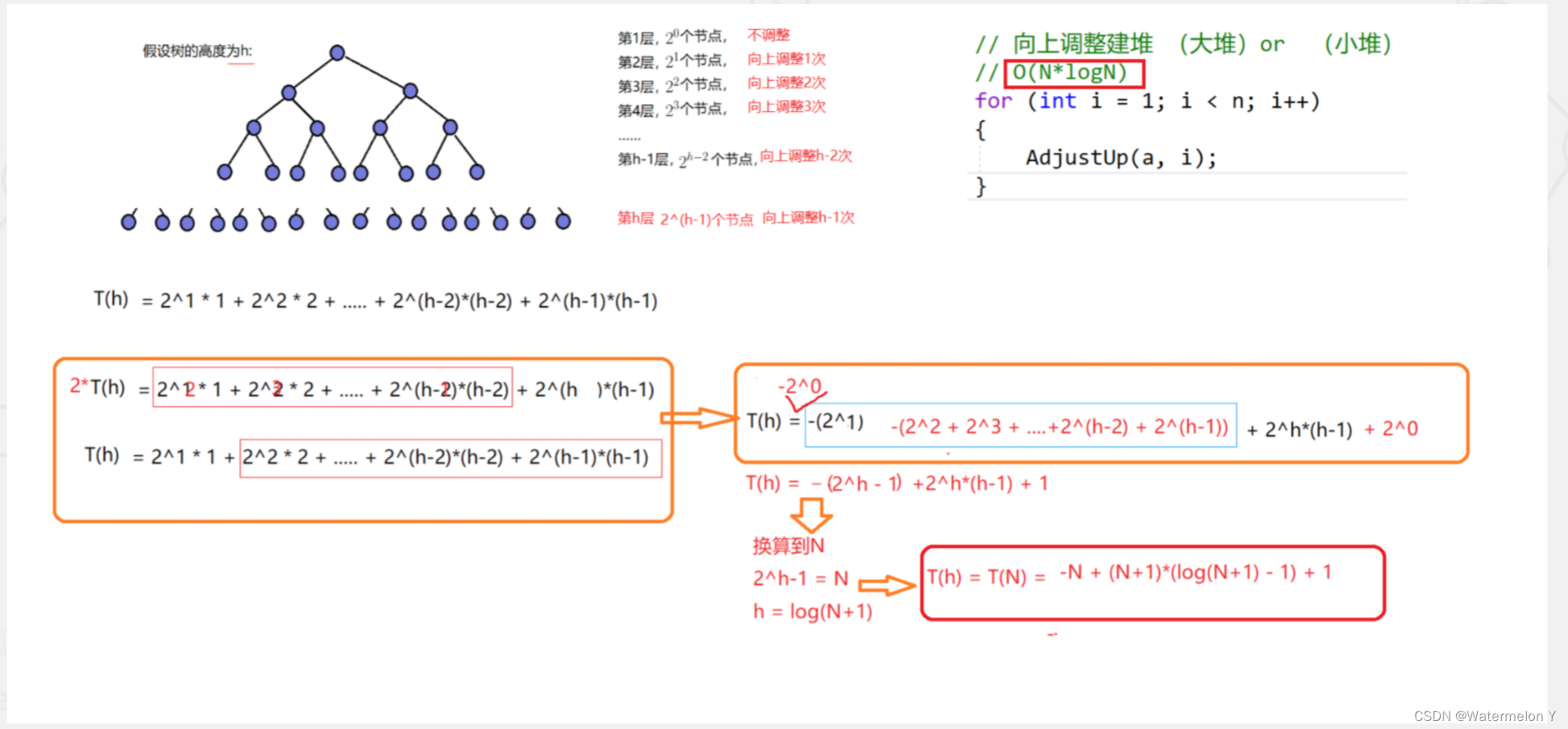
这样建堆的方式对时间复杂度有什么优化吗?

四 TOP-K问题
TOP - K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top - K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N - K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
#include<stdio.h>
#include<stdlib.h>
#include<time.h>typedef int HPDataType;void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void PrintTopK(const char* filename, int k)
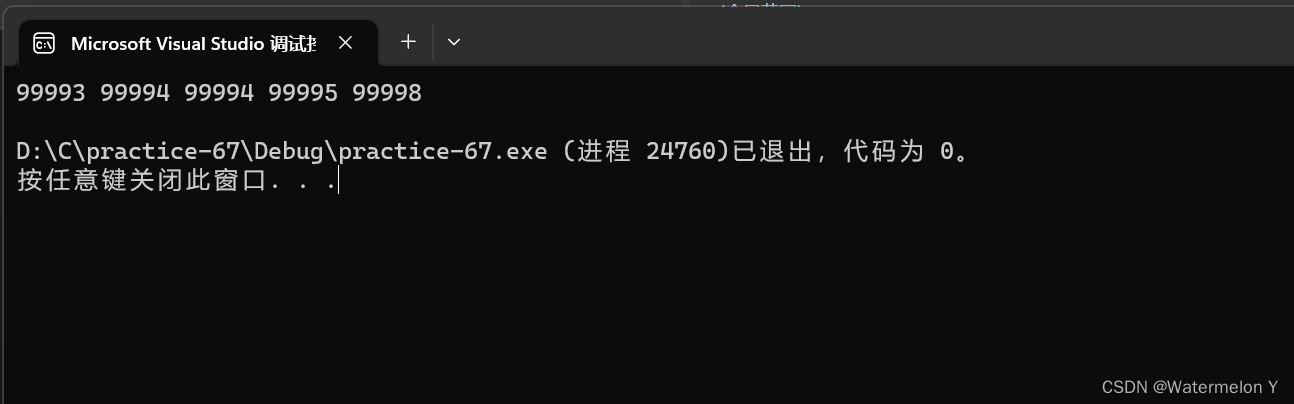
{//1 建堆--用a中前K个元素建堆(小堆)FILE* fout = fopen(filename, "r");if (fout == NULL){perror("fopen fail");return;}int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc fail");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);}//前K个建小堆for (int i = (k-2) / 2; i >= 0; i--){AdjustDown(minheap, k, i);}//2 将剩余n-k元素与堆顶元素比较, 满足就交换int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > minheap[0]){//替换进堆minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");fclose(fout);}void CreateDate()
{//造数据int n = 100000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; i++){int x = (rand() + i) % n;fprintf(fin, "%d\n", x);}fclose(fin);
}int main()
{CreateDate();PrintTopK("data.txt", 5);return 0;
}
本节对前面的二叉树基础很高, 没有理解的, 可以翻看我之前对二叉树顺序结构及其实现的章节.
继续加油!
相关文章:

【数据结构】二叉树--堆排序
目录 一 降序(建小堆) 二 升序 (建大堆) 三 优化(以升序为例) 四 TOP-K问题 一 降序(建小堆) void Swap(int* x, int* y) {int tmp *x;*x *y;*y tmp; }//降序 建小堆 void AdjustUp(int* a, int child) {int parent (child - 1) / 2;while (child > 0){if (a[chil…...

项目log日志mysql记录,熟悉python的orm框架
直接在项目里面创建一个class,这个类对应着mysql里面的表 我们运行项目,可以自动建立表 在.env中找到mysql的配置信息,这个是在NB服务器上运行的mysql,localhost需要变成NB服务器的ipv4地址 使用Mysql工具连接查看,连…...
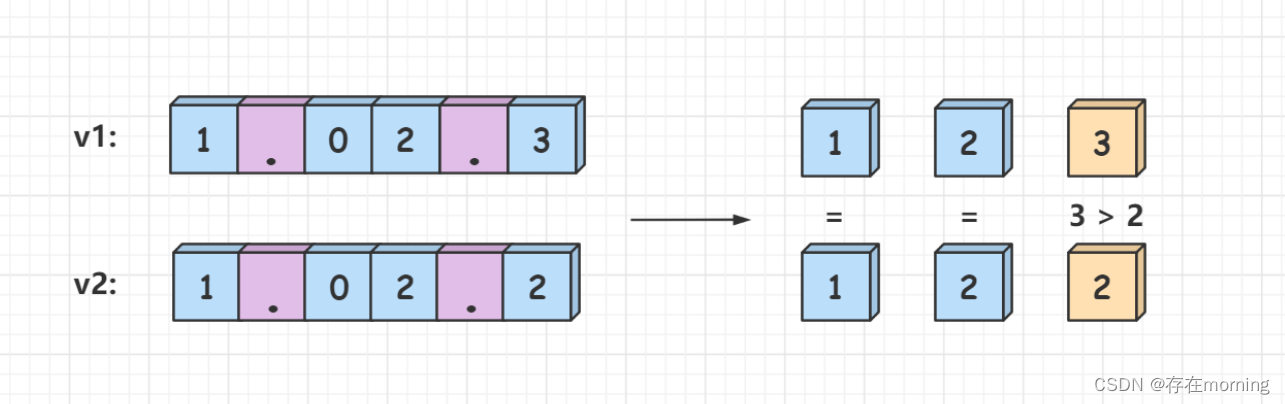
【数据结构-字符串 四】【字符串识别】字符串转为整数、比较版本号
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【字符串转换】,使用【字符串】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…...

React 组件传 children 的各种方案
自定义组件的时候往往需要传 children,由于写法比较多样,我就总结了一下。 方案列表 1. 类组件1.1 类组件,不使用解构1.2 类组件,使用解构 2. 函数组件2.1 函数组件,不使用解构2.2 函数组件,外部解构2.3 函…...
如何在一个传统的html中,引入vueJs并使用vue复制组件?
如何在一个传统的html中,引入vueJs并使用vue复制组件? 1.1 引言1.2 背景1.3 解决方案1.3.1 解决方案一:直接使用clipboard(不推荐仅供参考学习)1.3.2 解决方案二:封装指令js库后使用 (推荐) 1.1 引言 这篇博文主要分享如何在一个…...

【轻松玩转MacOS】故障排除篇
引言 在使用 MacOS 时,遇到故障是在所难免的。不要担心,这篇文章将为您提供一些常见的故障排除步骤,并介绍如何联系苹果的支持团队寻求帮助。让我们一起来看看吧! 一、常见的故障排除步骤 1.1 网络连接问题 如果你发现你的Mac…...

Linux基本指令(1)
Linux基本指令(1) 1.ls指令1.1ls的用法 2. pwd指令3.cd指令3.1 cd3.2补充内容3.3 cd - 指令3.4 cd ~ 指令 4. touch指令4.1stat指令 5.mkdir 指令6.rmdir/rm指令6.1补充内容 7.man指令8.nano 指令9.cat指令10 cp指令11 mv指令12 echo指令12.1 > 输出重…...

计算机毕业设计选题推荐-springboot 网上手机销售系统
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...
2、vscode c++ 项目配置调试及运行
文章目录 1、项目布局2、多项目管理2.1 先是一个总的CMakeLists.txt2.2 每个项目2.3 多版本OPENCV 3、调试和运行 接上一篇文章,vscode和cmake的c环境配置好以后,我们要写项目,再写对应的CMakeLists.txt 1、项目布局 . ├── bin ├── bu…...

二叉搜索树的最近公共祖先
二叉搜索树的最近公共祖先-力扣 235 题 求二叉搜索树最近公共祖先(祖先也包括自己) 前提: 1.节点值唯一 2.p和q都存在 要点:若 p,q 在 ancestor 的两侧,则 ancestor 就是它们的最近公共祖先 解题思路&…...
-- i2c - I2C操作)
LuatOS-SOC接口文档(air780E)-- i2c - I2C操作
常量 常量 类型 解释 i2c.FAST number 高速 i2c.SLOW number 低速 i2c.exist(id) i2c编号是否存在 参数 传入值类型 解释 int 设备id, 例如i2c1的id为1, i2c2的id为2 返回值 返回值类型 解释 bool 存在就返回true,否则返回false 例子 -- 检查i2c1是否存…...

帝国cms改目录后打不开,帝国cms改目录生成后还是404
帝国CMS更改了网站域名或者栏目目录地址信息打不开的解决方法,一起来看看吧: 很多的小伙伴们,改了后台的系统设置里面的网站地址或者栏目目录地址,信息页就打不开的解决方法如下: 后台>系统>数据更新>更新信…...
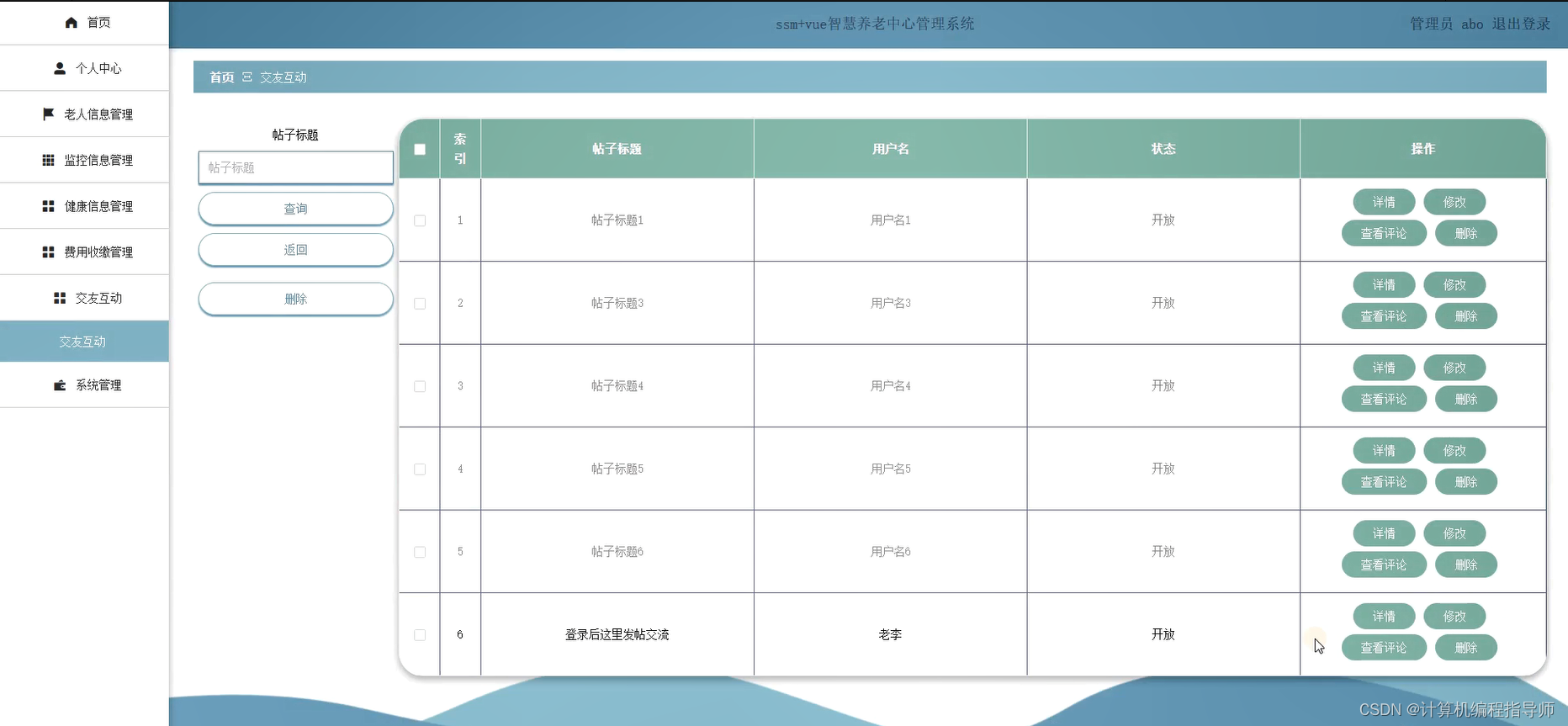
计算机毕业设计选什么题目好?springboot智慧养老中心管理系统
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...
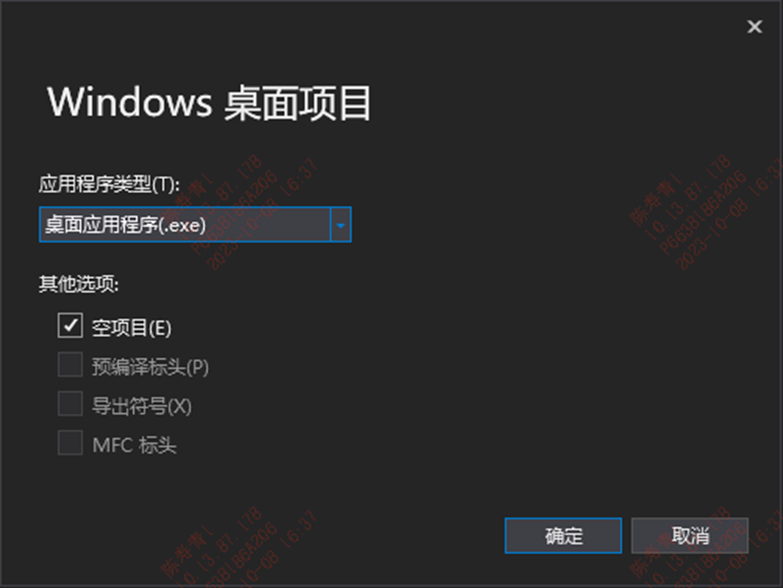
创建一个基本的win32窗口
1.建立一个窗口的基本步骤 (1)向系统注册一个窗体类 (2)根据窗体类创建窗口 (3)进入消息循环 2.程序结构 (1)主函数的输入参数 int WINAPI WinMain( HISTANCE hInstance,//当前窗口的句柄 HINSTANCE hPr…...

如何在 Spring Boot 中使用 WebSocket
在Spring Boot中使用WebSocket构建实时应用 WebSocket是一种用于实现双向通信的网络协议,它非常适合构建实时应用程序,如在线聊天、实时通知和多人协作工具。Spring Boot提供了对WebSocket的支持,使得在应用程序中集成WebSocket变得非常容易…...

ubuntu2023装完显卡驱动和CUDA CUDNN开机只有下划线闪烁
解决方法 网上很多方案,如Ubuntu开机后卡死只有左上角有一个下划线不停闪烁_ubuntu开机左上角横杠一直闪-CSDN博客,原因是显卡驱动和系统内核不兼容,解决方案是CtrlAltF2打开tty模式进行问题检查 但是我CtrlAltF2完全没反应。 于是…...
)
MySQL三种安装方法(yum安装、编译安装、二进制安装)
mysql安装 一、yum安装方式二、编译安装方式三、二进制安装方式 切记:一定要关闭防火墙和selinux!!! 服务器配置:2C4G即可,一台 一、yum安装方式 mysql的官方网站:www.mysql.com 中文官网&…...

《视觉 SLAM 十四讲》第 7 讲 视觉里程计1 【如何根据图像 估计 相机运动】【特征点法】
github源码链接V2 文章目录 第 7 讲 视觉里程计17.1 特征点法7.1.1 特征点7.1.2 ORB 特征FAST 关键点 ⟹ \Longrightarrow ⟹ Oriented FASTBRIEF 描述子 7.1.3 特征匹配 7.2 实践 【Code】本讲 CMakeLists.txt 7.2.1 使用 OpenCV 进行 ORB 的特征匹配 【Code】7.2.2 手写 O…...
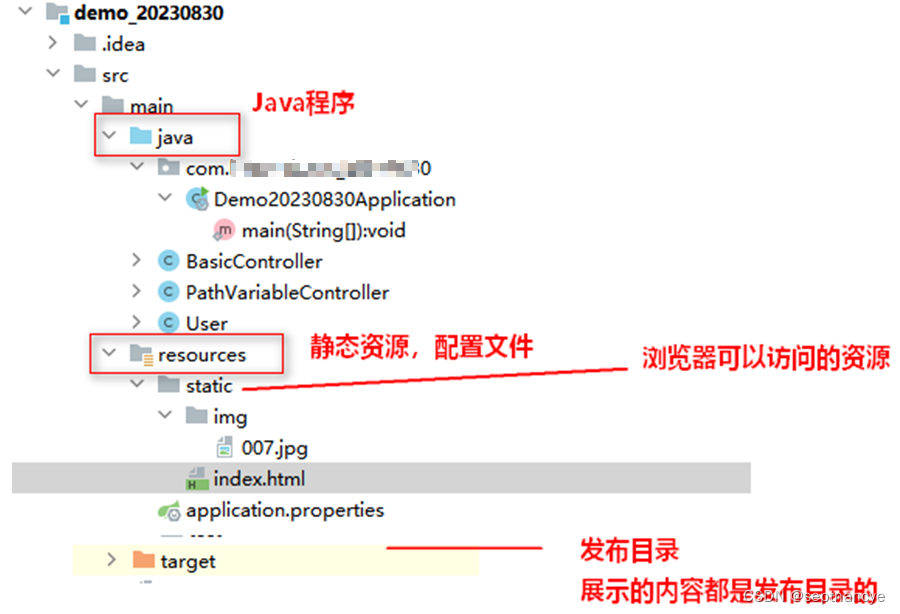
9. 一个SpringBoot项目运行
新手如何运行一个SpringBoot项目 1.SpringBoot项目运行 新创建的SpringBoot项目如何运行 2.启动lombok注解 点击该按钮,启动lombok注解支持 3.展示说明...
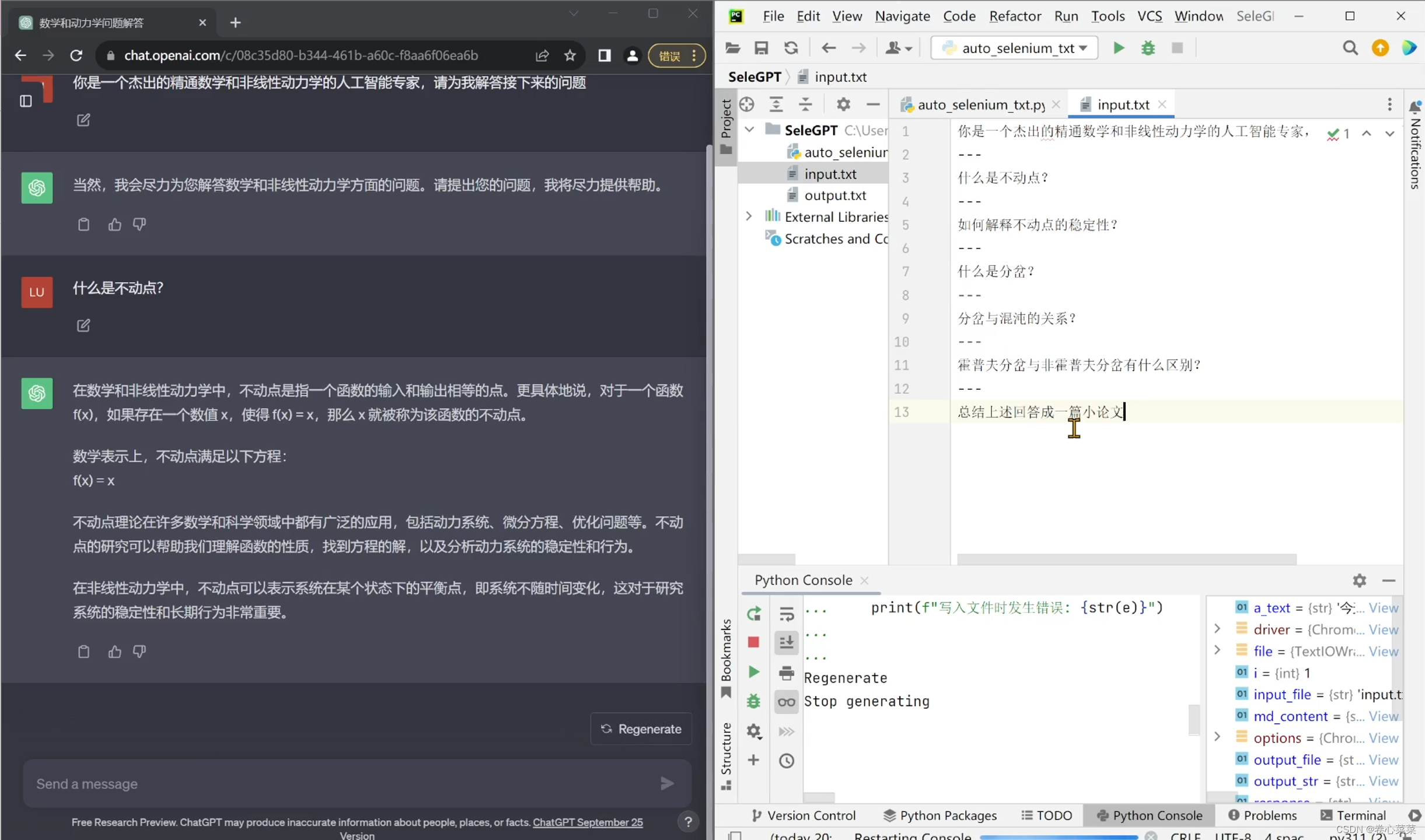
如何实现chatGPT批量问答,不用token
一、背景 因为需要批量提取一本教材里的概念做成知识图谱,想用chatGPT做概念提取。 调用api?别想了… 免费帐户的api慢得一批于是想用模仿人类交互的方法来调用,本来想用pyautogui的,但是主要是与浏览器交互,还是用s…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...