根据前序遍历结果构造二叉搜索树
根据前序遍历结果构造二叉搜索树-力扣 1008 题
题目说明:
1.preorder 长度>=1
2.preorder 没有重复值
直接插入
解题思路:
数组索引[0]的位置为根节点,与根节点开始比较,比根节点小的就往左边插,比根节点大的就往右边插,插入的前提是要插入的位置是Null
注意:根据前序遍历的结果,可以唯一地构造出一个二叉搜索树
对于前序遍历不是太理解的,作者推荐适合小白的文章:
二叉树的初步认识_加瓦不加班的博客-CSDN博客
// 8 5 1 7 10
/*
8
/ \
5 10
/ \ \
1 7 12
*/
// 8 5 1 7 10
/*8/ \5 10/ \ \1 7 12*/
public TreeNode bstFromPreorder(int[] preorder) {//数组索引[0]的位置为根节点TreeNode root = insert(null, preorder[0]);for (int i = 1; i < preorder.length; i++) {insert(root, preorder[i]);}return root;
}private TreeNode insert(TreeNode node, int val) {//找到空位了就创建一个新节点将val插入进去if (node == null) {return new TreeNode(val);}if(val < node.val) {//继续查询空位 如果查询到空位,要和父节点建立关系node.left = insert(node.left, val);} else if(node.val < val){node.right = insert(node.right, val);}return node;
}上限法

解题思路:
//依次处理prevorder中每个值,返回创建好的节点或者null
//1.如果超过上限,返回null 作为孩子返回
//2.如果没超过上限,创建节点,并设置其左右孩子
// 左右孩子完整后返回
//依次处理prevorder中每个值,返回创建好的节点或者null
//1.如果超过上限,返回null 作为孩子返回
//2.如果没超过上限,创建节点,并设置其左右孩子
// 左右孩子完整后返回
public TreeNode bstFromPreorder(int[] preorder) {return insert(preorder, Integer.MAX_VALUE);
}int i = 0;
private TreeNode insert(int[] preorder, int max) {//递归结束条件if (i == preorder.length) {return null;}int val = preorder[i];System.out.println(val + String.format("[%d]", max));if (val > max) {//如果超过上限,返回null 作为孩子返回return null;}//如果没超过上限,创建节点,并设置其左右孩子TreeNode node = new TreeNode(val);i++;node.left = insert(preorder, node.val); node.right = insert(preorder, max); return node;
}依次处理 prevorder 中每个值, 返回创建好的节点或 null 作为上个节点的孩子
如果超过上限, 返回 null
如果没超过上限, 创建节点, 并将其左右孩子设置完整后返回
i++ 需要放在设置左右孩子之前,意思是从剩下的元素中挑选左右孩子
分治法
解题思路:
//分治法 8,5,1,7,10,12
//8根 左:5,1,7 右:10,12
//5根 左:1 右:7
//10根 左:null 右:12//我们如何去分治呢?首先我们找到的是 题目给出的是前序遍历出来的,那么我们只要找到比根节点大的数开始就可以区分左、右子树的范围
//分治法 8,5,1,7,10,12
//8根 左:5,1,7 右:10,12
//5根 左:1 右:7
//10根 左:null 右:12//我们如何去分治呢?首先我们找到的是 题目给出的是前序遍历出来的,那么我们只要找到比根节点大的数开始就可以区分左、右子树的范围
public TreeNode bstFromPreorder(int[] preorder) {return partition(preorder, 0, preorder.length - 1);
}
//int start, int end 告诉处理范围
private TreeNode partition(int[] preorder, int start, int end) {//结束条件if (start > end) {return null;}//获取根节点 创建根节点对象TreeNode root = new TreeNode(preorder[start]);//跳过根节点开始找左、右子树的范围int index = start + 1;//条件是一直找到区域的结束while (index <= end) {//区分左、右子树的范围if (preorder[index] > preorder[start]) {break;}index++;}//此时 index 就是左、右子树的分界线root.left = partition(preorder, start + 1, index - 1);root.right = partition(preorder, index, end);return root;
}
刚开始 8, 5, 1, 7, 10, 12,方法每次执行,确定本次的根节点和左右子树的分界线
第一次确定根节点为 8,左子树 5, 1, 7,右子树 10, 12
对 5, 1, 7 做递归操作,确定根节点是 5, 左子树是 1, 右子树是 7
对 1 做递归操作,确定根节点是 1,左右子树为 null
对 7 做递归操作,确定根节点是 7,左右子树为 null
对 10, 12 做递归操作,确定根节点是 10,左子树为 null,右子树为 12
对 12 做递归操作,确定根节点是 12,左右子树为 null
递归结束,返回本范围内的根节点
相关文章:

根据前序遍历结果构造二叉搜索树
根据前序遍历结果构造二叉搜索树-力扣 1008 题 题目说明: 1.preorder 长度>1 2.preorder 没有重复值 直接插入 解题思路: 数组索引[0]的位置为根节点,与根节点开始比较,比根节点小的就往左边插,比根节点大的就往右…...

微信小程序指定某个元素强制重新渲染
之前写过 vue强制让某个元素重新渲染 利用了vue中的 v-if会控制元素是否挂载 以及 $nextTick 等待响应式更改生效再执行的特性 小程序也都有类似的方法 我们可以这样 wxml <view wx:if"{{min true}}">你好</view>用 wx:if 作用和v-if是一样的 js th…...
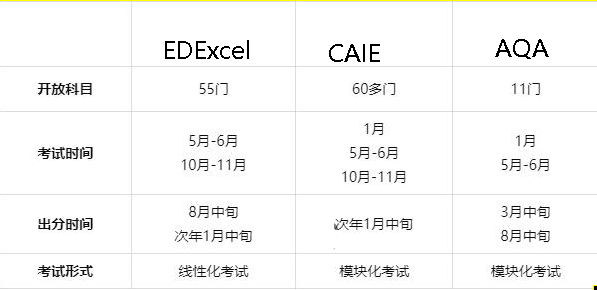
国际教材概念基础
各种区别 缩写 A-LEVEL(大学预科):General Certificate of Education Advanced Level AP:Advanced Placement(美国地区:美高AP) GCSE:General Certificate of Secondary Educati…...

2023全国大学生软件测试大赛开发者测试练习题满分答案(PairingHeap2023)
2023全国大学生软件测试大赛开发者测试练习题满分答案(PairingHeap2023) 题目详情题解代码(直接全部复制到test类中即可) 提示:该题只需要分支覆盖得分即可,不需要变异得分 题目详情 题解代码(…...

介绍一下tokens
“Tokens” 是一个计算机科学和自然语言处理领域常用的术语,通常用于表示文本中的最小单位。在这个上下文中,我将解释一下 “tokens” 的含义以及它们在不同领域中的用途: 自然语言处理 (NLP): 在自然语言处理中,“token” 是指文…...
机器学习、深度学习相关的项目集合【自行选择即可】
【基于YOLOv5的瓷砖瑕疵检测系统】 YOLOv5是一种目标检测算法,它是YOLO(You Only Look Once)系列模型的进化版本。YOLOv5是由Ultralytics开发的,基于一阶段目标检测的概念。其目标是在保持高准确率的同时提高目标检测的速度和效率…...
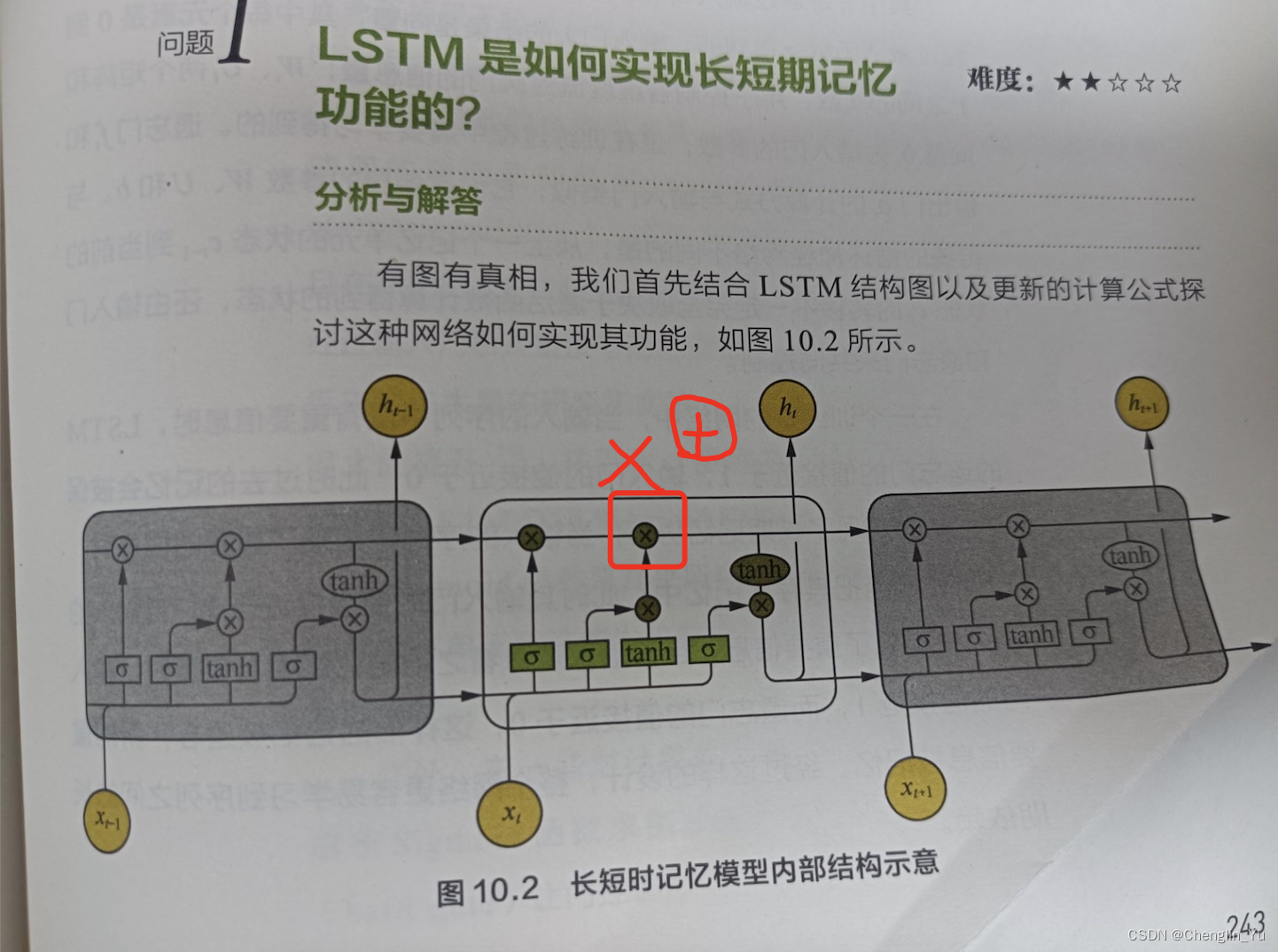
百面机器学习书刊纠错
百面机器学习书刊纠错 P243 LSTM内部结构图 2023-10-7 输入门的输出 和 candidate的输出 进行按元素乘积之后 要和 遗忘门*上一层的cell state之积进行相加。...

vue2安装cesium并使用
一、安装 1.安装cesium npm install cesium1.95.0 -S 2.安装所需 npm install copy-webpack-plugin10.2.4 -D 二、配置 1.配置vue.config.js vue 中引入cesium 需要用copy-webpack-plugin 把一些文件拷贝到打包目录 // vue.config.js const CopyWebpackPlugin require…...
基于Docker来部署Nacos的注册中心
基于Docker来部署Nacos的注册中心 准备MySQL数据库表nacos.sql,用来存储Nacos的数据。 最终表结构如下: 在本地nacos/custom.env文件中,有一个MYSQL_SERVICE_HOST也就是mysql地址,需要修改为你自己的虚拟机IP地址: …...

黑马JVM总结(三十一)
(1)类加载器-概述 启动类加载器-扩展类类加载器-应用程序类加载器 双亲委派模式: 类加载器,加载类的顺序是先依次请问父级有没有加载,没有加载自己才加载,扩展类加载器在getParent的时候为null 以为Boots…...

【C++】list基本接口+手撕 list(详解迭代器)
父母就像迭代器,封装了他们的脆弱...... 手撕list目录: 一、list的常用接口及其使用 1.1list 构造函数与增删查改 1.2list 特殊接口 1.3list 排序性能分析 二、list 迭代器实现(重点难点) 关于迭代器的引入知识:…...

PowerShell pnpm : 无法加载文件 C:\Users\lenovo\AppData\Roaming\npm\pnpm.ps1
1、右键点击【开始】,打开Windows PowerShell(管理员) 2、运行命令set-ExecutionPolicy RemoteSigned 3、根据提示,输入A,回车 此时管理员权限已经可以运行pnpm 如果vsCode还报该错误 继续输入 4、右键点击【开始】,打…...

mysql面试题33:Blob和text有什么区别
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:Blob和text有什么区别 Blob和text是数据库中存储大文本数据的两种数据类型&#…...

docker版jxTMS使用指南:4.6版升级内容
4.6版jxTMS已经发布,升级了多个重大能力,本系列文章将逐一进行讲解。 docker版本的使用,请查看:docker版jxTMS使用指南 4.0版jxTMS的说明,请查看:4.0版升级内容 4.2版jxTMS的说明,请查看&…...

java最优建树算法
建树算法 树的数据结构 {"code": "1111","name": "","parentcode": "0000","children": null }, {"code": "2222","name": "","parentcode": &q…...

mysql面试题30:什么是数据库连接池、应用程序和数据库建立连接的过程、为什么需要数据库连接池、你知道哪些数据库连接池
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:什么是数据库连接池? 数据库连接池是一种用于管理和复用数据库连接的技术。它是在应用程序和数据库之间建立一组数据库连接,并以池的形式存储起…...
【Vue】vscode格式刷插件Prettier以及配置项~~保姆级教程
文章目录 前言一、下载插件二、在项目内创建配置文件1.在根目录创建,src同级2.写入配置3.每个字段含义 总结 前言 vscode格式刷,有太多插件了,但是每个的使用,换行都不一样。 这里我推荐一个很多人都推荐了的Prettier 一、下载插…...
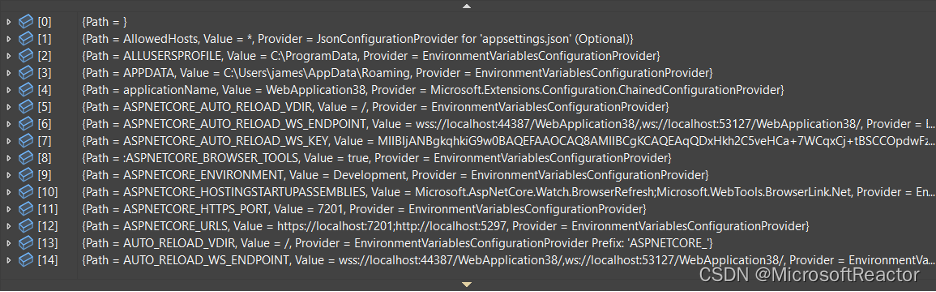
.NET 8 中的调试增强功能
作者:James Newton-King 排版:Alan Wang 开发人员喜欢 .NET 强大且用户友好的调试体验。您可以在您选择的 IDE 中设置断点,启动已经附加上调试器的程序,逐步执行代码并查看 .NET 应用程序的状态。 在 .NET 8 中,我们致…...
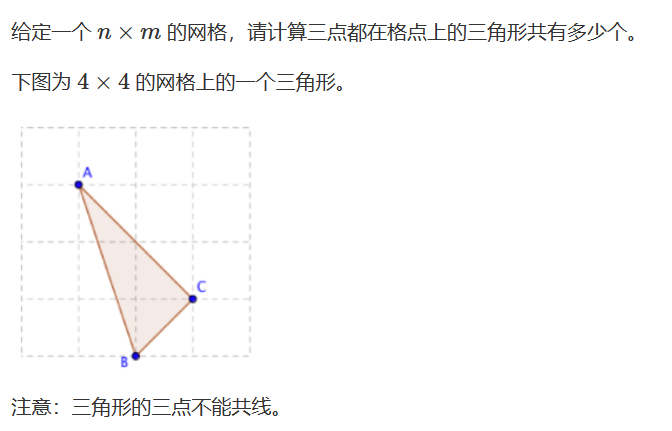
1310. 数三角形
知识点:(a, b)与(c, d)两点连线上点的个数为:gcd(x, y) 1(包括端点) (设横坐标差的绝对值为x, 纵坐标差的绝对值为y ) 思路:先算出选三个点的所有情况,再减去三点共线的情况 共线的斜率为0时特判 当共线…...
数据库基础(一)
数据库面试基础 注,本文章内容主要来自于JAVAGUIDE,只是结合网上资料和自己的知识缺陷进行一点补充,需要准备面试的请访问官方网址。 一、范式 参考链接 函数依赖:一张表中,确定X则必定能确定Y,则X->…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
