内排序算法
排序算法是面试中常见的问题,不同算法的时间复杂度、稳定性和适用场景各不相同。按照数据量和存储方式可以将排序算法分为 内排序(Internal Sorting)和 外排序(External Sorting)。
内排序是指对所有待排序的数据都可以一次性加载到内存中进行排序。这意味着所有的数据都可以直接在计算机的内存中操作,无需借助外部存储设备(如硬盘)。内排序算法的设计可以更加灵活,因为内存操作速度远远高于磁盘操作速度。常见的内排序算法包括快速排序、归并排序、插入排序、冒泡排序等。
外排序是指对大量数据进行排序时,由于数据无法一次性加载到内存中,需要借助外部存储设备进行排序。通常在外排序中,数据会被分成若干个小块,每次只处理其中一部分数据,然后将部分排序好的数据存储回外部存储设备,再进行合并等操作。外排序算法需要考虑数据的分块、读写外部存储的效率,以及合并有序数据等问题。常见的外排序算法有多路归并排序、置换选择排序等。
本文介绍的都是常见的内排序算法:插入排序、冒泡排序、选择排序、希尔排序、归并排序、快速排序、堆排序、桶排序。
目录
- 1. 插入排序
- 2. 冒泡排序
- 3. 选择排序
- 4. 希尔排序
- 5. 归并排序
- 6. 快速排序
- 7. 堆排序
- 8. 桶排序
1. 插入排序
插入排序的核心是将待排序的元素逐个插入到已经排好序的序列中,以构建有序的输出序列:
void inssort(int A[],int n){for(int i=1;i<n;i++){for(int j=i;j>0;j--){if(A[j]<A[j-1]){ //A[j]<A[j-1](此处小于即排在前面)swap(A,j,j-1);}else{break; //A[j]已达到正确位置(时间优化)}}}
}
插入排序的平均时间复杂度为 O(n2),最好情况为 O(n),最坏情况为 O(n2),适用于小规模的数据集或者已经基本有序的数据。插入排序的空间复杂度为 O(1),是一种稳定排序算法。
2. 冒泡排序
冒泡排序的核心思想是通过比较相邻的元素并交换位置,逐渐将最小的元素 “冒泡” 到正确的位置。冒泡排序的过程类似于冒泡泡沫在水中升起的过程,较大的元素会逐渐向序列的开头 “冒泡”:
void bubsort(int A[],int n){for(int i=0;i<n-1;i++){for(int j=n-1;j>i;j--){if(A[j]<A[j-1]){swap(A,j,j-1);}}}
}
冒泡排序的平均时间复杂度为 O(n2),最好情况和最坏情况都为 O(n2)。冒泡排序的空间复杂度为 O(1),是一种稳定排序算法。
3. 选择排序
选择排序的核心思想是在未排序序列中选择最小的元素,然后将它与未排序序列的起始位置交换,使得已排序序列逐步增长:
void selsort(int A[],int n){for(int i=0;i<n-1;i++){int index=i;for(int j=n-1;j>i;j--){if(A[j]<A[index]){index=j;}}swap(A,i,index);}
}
选择排序的平均时间复杂度为 O(n2),最好情况和最坏情况都为 O(n2)。选择排序的空间复杂度为 O(1),是一种稳定排序算法。
4. 希尔排序
希尔排序利用了插入排序最佳时间代价特性,在不相邻的记录之间进行交换和比较。核心思想是将整个序列分成多个较小的子序列来逐步减少序列的无序度,从而在最后一步进行一次插入排序,达到提高排序速度的效果。过程如图:

void inssort2(int A[],int n,int incr){ //n为传入数组长度,incr为数组内元素间隔for(int i=incr;i<n;i+=incr){ //incr相当于第1位元素,+incr相当于间隔for(int j=i;(j>=incr)&&(A[j]<A[j-incr]);j-=incr){int tmp=A[j];A[j]=A[j-incr];A[j-incr]=tmp;cnt1++;}}
}
void shellsort(int A[],int n){for(int i=n/2;i>2;i/=2){ //i表示组数或者间隔for(int j=0;j<i;j++){ //j表示有i组数据时从0到i遍历inssort2(&A[j],n-j,i); //对第j组数据进行插入排序(起始位置,长度,间隔)//第j组数据在A中下标:j,j+i,j+2i...用inssort2中传入参数表示为:&A[j],&A[j]+i,&A[j]+2i...}}inssort2(A,n,1); //对整个数组插入排序
}
希尔排序在现实中没有对应的直观解释,也无法证明其时间复杂度,一般认为平均时间复杂度为 O(n1.5),最好情况为 O(nlogn),最坏情况为 O(n2)。希尔排序的空间复杂度为 O(1),是一种不稳定排序算法。
5. 归并排序
归并排序的核心思想是 “二分+合并”,即将一个未排序的数组分割成两个子数组,递归地对这两个子数组排好序后再合并为一整个有序的数组:
void mergesort(int A[],int tmp[],int left,int right){ //left表示A[0]下标,right表示A[n-1]下标if(left==right) return;int mid=(left+right)/2;mergesort(A,tmp,left,mid); //向下递归,二分集合并排序mergesort(A,tmp,mid+1,right);for(int i=left;i<=right;i++){tmp[i]=A[i];}int i1=left,i2=mid+1; //i1,i2表示两个待合并数组(各自都已排序)首个未排序元素下标for(int curr=left;curr<=right;curr++){if(curr==mid+1){ //left数组已完成合并A[curr]=tmp[i2++];}else if(i2>right){ //right数组已完成合并A[curr]=tmp[i1++];}else if(tmp[i1]<tmp[i2]){A[curr]=tmp[i1++];}else{A[curr]=tmp[i2++];}}
}
归并排序的平均时间复杂度为 O(nlogn),最好情况和最坏情况也都为 O(nlogn)。归并排序的空间复杂度为 O(n),是一种稳定排序算法。
6. 快速排序
快速排序的核心思想是选择一个轴值 pivot,将数组分为小于轴值的部分和大于轴值的部分,然后递归地对这两部分进行排序。轴值的选择会影响算法的效率,一般选取数组的中间点作为轴值。为了设计方便,会将轴值置于数组末端,待排好序后再移动到合适位置:
//partition函数将数组的l+1~r-1划分为两个以轴值为分界的部分,并返回轴值的下标(实际上该位元素与最后一位交换后才是真正的轴值下标)
int partition(int A[],int l,int r,int& pivot){ //l,r为A[]的左右范围,pivot为轴值do{while(A[++l]<pivot); //跳过满足小于轴值的元素,终止在大于轴值的地方while((l<r)&&(A[--r]>pivot));int tmp=A[r];A[r]=A[l];A[l]=tmp;}while(l<r);return l;
}void qsort(int A[],int i,int j){if(i>=j) return;int pivotindex=(i+j)/2; //选取轴值int pivot=A[pivotindex];A[pivotindex]=A[j]; //将轴值与末尾元素互换A[j]=pivot;pivotindex=partition(A,i-1,j,A[j]); //将l+1~r-1按轴值分部,并返回待与轴值交换元素下标pivot=A[j]; //轴值还在末尾等待交换A[j]=A[pivotindex];A[pivotindex]=pivot;qsort(A,i,pivotindex-1);qsort(A,pivotindex+1,j);
}
快速排序是迄今为止所有内排序算法中在平均情况下最快的一种,当每个轴值都把数组分成相等的两个部分时,整个算法的时间代价是 Θ \Theta Θ(nlogn)。快速排序的平均时间复杂度为 O(nlogn),最好情况为 O(nlogn),最坏情况为 O(n2)。快速排序的空间复杂度为 O(logn),是一种不稳定排序算法。
7. 堆排序
堆排序是基于堆数据结构的排序算法,它利用最小堆的性质来实现对数组的排序:
class heap{
private:int* Heap;int maxsize;int n;void siftdown(int pos){while(!isLeaf(pos)){int j=leftchild(pos); //下面j表示的是lc和rc中较小值的下标int rc=rightchild(pos);if((rc<n)&&(Heap[rc]<Heap[j])){j=rc;}if(Heap[pos]<Heap[j]){return;}int tmp=Heap[pos];Heap[pos]=Heap[j];Heap[j]=tmp;pos=j;}}
public:heap(int* h,int num,int max){Heap=h;n=num;maxsize=max;buildHeap();}int size(){return n;}bool isLeaf(int pos){return (pos>=n/2)&&(pos<n);}int leftchild(int pos){return 2*pos+1;}int rightchild(int pos){return 2*pos+2;}int parent(int pos){return (pos-1)/2;}void buildHeap(){for(int i=n/2-1;i>=0;i--){siftdown(i);}}void insert(const int& it){int curr=n++;Heap[curr]=it;while((curr!=0)&&(Heap[curr]<Heap[parent(curr)])){int tmp=Heap[curr];Heap[curr]=Heap[parent(curr)];Heap[parent(curr)]=tmp;curr=parent(curr);}}int removefirst(){n--;int tmp=Heap[0];Heap[0]=Heap[n];Heap[n]=tmp;if(n!=0){siftdown(0);}return Heap[n];}int remove(int pos){if(pos==(n-1)){n--;}else{n--;int tmp=Heap[pos];Heap[pos]=Heap[n];Heap[n]=tmp;while((pos!=0)&&(Heap[pos]<Heap[parent(pos)])){int tmp=Heap[pos];Heap[pos]=Heap[parent(pos)];Heap[parent(pos)]=tmp;pos=parent(pos);}if(n!=0){siftdown(pos);}}return Heap[n];}
};
void heapsort(int A[],int n){int minval;heap H(A,n,n);for(int i=0;i<n;i++){minval=H.removefirst();}
}
堆排序的平均时间复杂度为 O(nlogn),最好情况和最坏情况也都为 O(nlogn),但比快速排序要慢一个常数因子。堆排序在实际使用时适用于查找第 k 大小的元素,或者用于外排序。堆排序的空间复杂度为 O(1),是一种不稳定排序算法。
8. 桶排序
桶排序的核心思想是将数组按数值范围放入若干个桶,每个桶对应一定范围的数据,然后对每个桶中的数据使用其他排序算法或递归方式进行排序,最后将所有桶中的数据按顺序合并得到排序结果:
void inssort(int A[],int n){for(int i=1;i<n;i++){for(int j=i;j>0;j--){if(A[j]<A[j-1]){int tmp=A[j];A[j]=A[j-1];A[j-1]=tmp;}else{break;}}}
}void bucketSort(int A[],int n,int numBuckets){//创建桶int buckets[numBuckets][n]; //二维数组,每行表示一个桶int bucketSizes[numBuckets]; //每个桶中元素的数量//初始化桶的大小for(int i=0;i<numBuckets;i++){bucketSizes[i]=0;}//确定数组元素范围int maxA=-999,minA=999;for(int i=0;i<n;i++){if(A[i]>maxA) maxA=A[i];if(A[i]<minA) minA=A[i];} //将元素放入桶中for(int i=0;i<n;i++){int bucketGap=ceil((maxA-minA)/(float)numBuckets);int bucketIndex=(A[i]-minA)/bucketGap;buckets[bucketIndex][bucketSizes[bucketIndex]++]=A[i];}//对每个桶中的元素进行插入排序for(int i=0;i<numBuckets;i++){inssort(buckets[i],bucketSizes[i]);}// 合并桶中的元素int index=0;for(int i=0;i<numBuckets;i++){for(int j=0;j<bucketSizes[i];j++){A[index++]=buckets[i][j];}}
}
桶排序的平均时间复杂度为 O(n2),最好情况和最坏情况也都为 O(n2),但比插入排序要快一个常数因子。桶排序适用于在已知输入数据的范围内进行排序,若数据分布不均匀也会影响效率。桶排序的空间复杂度为 O(n2),是一种稳定排序算法。
相关文章:

内排序算法
排序算法是面试中常见的问题,不同算法的时间复杂度、稳定性和适用场景各不相同。按照数据量和存储方式可以将排序算法分为 内排序(Internal Sorting)和 外排序(External Sorting)。 内排序是指对所有待排序的数据都可…...

options.html 页面设计成聊天框,左侧是功能列表,右侧是根据左侧的功能切换成不同的内容。--chatGpt
gpt: 要将 options.html 页面设计成一个聊天框式的界面,其中左侧是功能列表,右侧根据左侧的功能切换成不同的内容,你可以按照以下步骤进行设计和实现: 1. 首先,创建 options.html 文件,并在其中定义基本的…...
排序算法-选择排序法(SelectionSort)
排序算法-选择排序法(SelectionSort) 1、说明 选择排序法也是枚举法的应用,就是反复从未排序的数列中取出最小的元素,加入另一个数列中,最后的结果即为已排序的数列。选择排序法可使用两种方式排序,即在所…...
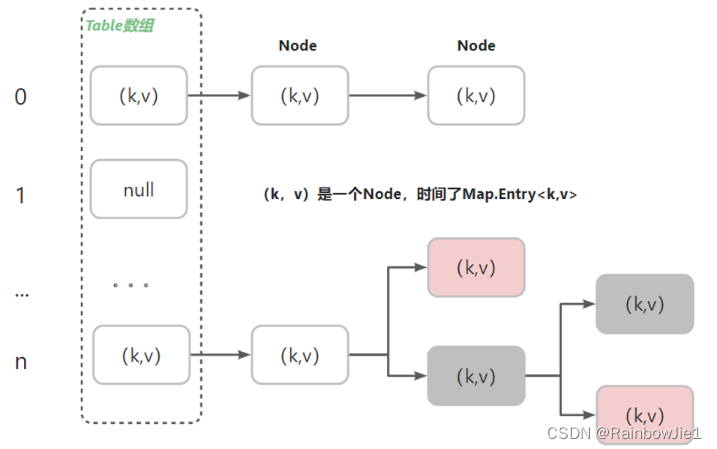
Java-集合框架
文章目录 摘要CollectionCollection集合遍历Iterator迭代器增强for循环 排序 ListArrayListLinkedListVector SetHashSet Map小结 摘要 Java的集合框架提供了一组用于存储、管理和操作数据的类和接口。这个框架提供了各种数据结构,如列表、集合、队列和映射&#x…...

联想携中国移动打造车路协同方案 助力重庆实现32类车联网场景
10月11日,联想集团在中国移动全球合作伙伴大会上首次分享了与中国移动等合作伙伴共同打造的5G车路协同案例——重庆两江协同创新区车路协同应用。联想利用基于5G智能算力技术,在总里程55公里路段实现了32类车联网场景。 据了解,重庆两江协同创…...
Rust入门基础
文章目录 Rust相关介绍为什么要用Rust?Rust的用户和案例 开发环境准备安装Rust更新与卸载Rust开发工具 Hello World程序编写Rust程序编译与运行Rust程序 Cargo工具Cargo创建项目Cargo构建项目Cargo构建并运行项目Cargo检查项目Cargo为发布构建项目 Rust相关介绍 为…...

民族民俗景区3d智慧旅游系统提升游客旅游体验和质量
随着科技的不断发展,传统的旅游方式正在逐渐被新的技术和系统所取代。网上3D沉浸式旅游体验凭借其身临其境的沉浸式体验优势,正成为旅游业的新宠。 网上3D沉浸式旅游体验是将旅游景区、度假区、休闲街区、科博馆等场所空间,利用VR全景制作、w…...

Webpack 解决:Error: error:0308010C:digital envelope routines::unsupported 的问题
1、问题描述: 其一、报错为: Error: error:0308010C:digital envelope routines::unsupported 中文为: 错误:错误:0308010C:数字信封例程::不支持 其二、问题描述为: 在项目打包的时候 np…...

JAVA操作Json的ObjectMapper类
JAVA操作Json的ObjectMapper类 市面上用于在 Java 中解析 Json 的第三方库,随便一搜不下几十种,其中的佼佼者有 Google 的 Gson以及本文的 jackson。 三者不相伯仲,随着掌握一个都能满足项目中的 json 解析操作,因为 Spring Boot…...

Docker--harbor
一,registry registry是私有仓库的核心,只有字符终端。 二,registry部署 #首先下载 registry 镜像 docker pull registry#在 daemon.json 文件中添加私有镜像仓库地址 vim /etc/docker/daemon.json {"insecure-registries": [&q…...

Flink中的时间和窗口
1.Flink的时间和窗口 在传统的批处理系统中,我们可以等到一批数据全部都到齐了之后,对其做相关的计算;但是在实时处理系统中,数据是源源不断的,正常情况下,我们就得来一条处理一条。那么,我们应…...

Ultra-Fast-Lane-Detection 车道线学习资料整理
目录 官方版本 两个优化 数据标注,降低参数量 1 数据标注 2降低参数量...

【Ubuntu】Ubuntu18.04终端卡顿问题
博主您好,我也遇到了类似的问题,但我找到了问题的原因: 在gnome-terminal中,按tab补全是默认开启了“咚咚咚”音效的,在gnome-terminal里把音效关掉就好了,主要是因为按tab时,NVIDIA的视频信号和…...

k8s强制删除pod、svc、namespace(Terminating)
如果名称空间、pod、pv、pvc全部处于“Terminating”状态时,此时的该名称空间下的所有控制器都已经被删除了,之所以出现pod、pvc、pv、ns无法删除,那是因为kubelet 阻塞,有其他的资源在使用该namespace,比如CRD等&…...

froeach迭代删除和List迭代删除问题
场景:我有一个 List<ISSLogMessage> records 数据,需要从里面删除指定内容数据 第一次写成 foreach(var item in records) {if (item.logMessage.Contains("上传通行记录"))records.Remove(item); } 直接报错,因为foreach 是个迭代器 直接移除它的对象会报…...

chromedriver下载地址
ChromeDriver下载地址: 淘宝镜像:https://registry.npmmirror.com/binary.html?pathchromedriver/ 官方镜像:https://sites.google.com/a/chromium.org/chromedriver/downloads在下载页面上,将看到一列Chrome浏览器的版本号和相…...

2ED2410-EM:12v / 24v智能模拟高侧MOSFET栅极驱动器
概述 12v / 24v智能模拟高侧MOSFET栅极驱动器。 特性 PRO-SIL ISO 26262-准备根据ISO 26262:2018条款8-13支持硬件元件评估的集成商。一个通道器件具有两个高侧栅极驱动器输出。3 Ω下拉,50 Ω上拉,用于快速开关开/关。支持背靠背MOSFET拓扑(共漏极和共源)。两个双向高侧模拟…...

什么是Fetch API?与传统的AJAX相比,有什么优势?
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...

43.241.18.123哪些问题会导致服务器里面时间错误
我们在使用服务器的过程中,有时候可能会发现,服务器里面时间跟标准的时间对不上,那服务器里面时间错误可能由哪些问题引起: 硬件问题:服务器硬件中的时钟或电池可能损坏或失效,导致时间不准确或重置为默认…...

【ElasticSearch】更新es索引生命周期策略,策略何时对索引生效
大家好,我是好学的小师弟,今天和大家讨论下更新es索引生命周期策略后,策略何时对索引生效 结论: 若当前索引已应用策略A(旧),更新完策略A后,新的策略A会立即对原来的已经应用该策略的索引生效;若当前索引…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...

自定义线程池1.2
自定义线程池 1.2 1. 简介 上次我们实现了 1.1 版本,将线程池中的线程数量交给使用者决定,并且将线程的创建延迟到任务提交的时候,在本文中我们将对这个版本进行如下的优化: 在新建线程时交给线程一个任务。让线程在某种情况下…...

【Vue】scoped+组件通信+props校验
【scoped作用及原理】 【作用】 默认写在组件中style的样式会全局生效, 因此很容易造成多个组件之间的样式冲突问题 故而可以给组件加上scoped 属性, 令样式只作用于当前组件的标签 作用:防止不同vue组件样式污染 【原理】 给组件加上scoped 属性后…...
——Oracle for Linux物理DG环境搭建(2))
Oracle实用参考(13)——Oracle for Linux物理DG环境搭建(2)
13.2. Oracle for Linux物理DG环境搭建 Oracle 数据库的DataGuard技术方案,业界也称为DG,其在数据库高可用、容灾及负载分离等方面,都有着非常广泛的应用,对此,前面相关章节已做过较为详尽的讲解,此处不再赘述。 需要说明的是, DG方案又分为物理DG和逻辑DG,两者的搭建…...
