【软考设计师】S01 数据结构 E01 线性结构 P01 线性表
线性表
- 前言——线性结构
- 线性表
- 线性表的定义
- 线性表的特点
- 线性表的存储结构
- 顺序存储
- 链式存储
- 单链表
- 双向链表
- 循环链表
- 静态链表
前言——线性结构
线性结构是一种基本的数据结构,主要用于对客观世界中具有单一前驱和后继的数据关系进行描述。线性结构的特点是数据元素之间呈现一种线性关系,即元素“一个接一个排列”。
线性表
线性表的定义
- 线性结构: 线性表是最简单、最基本也是最常用的一种线性结构;
- 存储结构: 顺序存储、链式存储;

- 基本操作: 插入、删除和查找;
线性表的特点
线性表可为空。非空线性表的特点如下:
- 存在唯一一个称为“第一个”的元素;
- 存在唯一一个称为“最后一个”的元素;
- 除第一个元素外,每个元素都有且只有一个直接前驱;
- 除最后一个元素外,每个元素都有且只有一个直接后继;
线性表的存储结构
线性表的存储结构分为顺序存储和链式存储。

顺序存储
基础概念:
- 精辟: 用一组地址连续的存储单元依次存储线性表中的数据元素,从而使得逻辑上相邻的两个元素在物理位置上也相邻。
- 公式: 以 L O C ( a 1 ) LOC(a_1) LOC(a1) 表示线性表中第一个元素的存储位置,在顺序存储结构中,第 i i i 个元素 a i a_i ai 的存储位置为: L O C ( a i ) = L O C ( a 1 ) + ( i − 1 ) ∗ L LOC(a_i) = LOC(a_1) + (i-1) * L LOC(ai)=LOC(a1)+(i−1)∗L 其中 L L L 表示每个数据元素所占空间的字节数。
- 优点: 可以随机存取表中的元素:根据上述的公式,我们可以根据计算关系得知表中任一个元素的位置。
- 缺点: 插入和删除操作需要移动元素:在插入前要移动元素以挪出空的存储单元,然后再插入元素;删除时同样需要移动元素,以填充被删除元素空出来的存储单元。
基本操作:
- 插入: 在表长为 n n n 的线性表中插入新元素时,共有 n + 1 n+1 n+1 个插入位置。在位置 1 1 1 插入新元素,表中原有 n n n 个元素都需要移动;在位置 n + 1 n+1 n+1 插入新元素时,不需要移动任何元素。因此等概率下,插入一个新元素需要移动的元素个数期望 E i n s e r t E_{insert} Einsert 为: E i n s e r t = ∑ i = 1 n + 1 P i ∗ ( n − i + 1 ) = 1 n + 1 ∑ i = 1 n + 1 ( n − i + 1 ) = n 2 E_{insert} = \sum ^{n+1} _{i=1} P_i *(n-i+1) = \frac 1 {n+1} \sum ^{n+1} _{i=1} (n-i+1) = \frac n 2 Einsert=i=1∑n+1Pi∗(n−i+1)=n+11i=1∑n+1(n−i+1)=2n 其中 P i P_i Pi 表示在表中的位置 i i i 插入新元素的概率。
- 删除: 在表长为 n n n 的线性表中删除元素时,共有 n n n 个可删除的元素。删除元素 a 1 a_1 a1 时需要移动 n − 1 n-1 n−1 个元素;删除元素 a n a_n an 时不需要移动元素。因此等概率下,删除一个元素需要移动的元素个数期望 E d e l e t e E_{delete} Edelete 为: E d e l e t e = ∑ i = 1 n q i ∗ ( n − i ) = 1 n ∑ i − 1 n ( n − i ) = n − 1 2 E_{delete} = \sum ^{n} _{i=1} q_i*(n-i)=\frac 1 n \sum ^{n} _{i-1} (n-i) = \frac {n-1} 2 Edelete=i=1∑nqi∗(n−i)=n1i−1∑n(n−i)=2n−1 其中 q i q_i qi 表示删除第 i i i 个元素(即 a i a_i ai)的概率。
链式存储

线性表的链式存储是通过指针链接起来的结点来存储数据元素,基本结点结构为:

其中数据域用于存储数据元素的值,指针域用于存储当前元素的直接前驱或直接后继的位置信息。指针域中的信息称为指针(或链)。
单链表
因为链式存储存储各元素的结点的地址并不要求是连续的,因此存储数据元素的同时必须存储元素之间的逻辑关系。结点与结点之间通过指针域构成一个链表,若节点中只有一个指针域,则称为单链表(或称线性链表)。

假设单链表中的元素是整型,则单链表结构类型的定义为:
typedef struct node{int data; /*结点的数据域,假设为整型*/struct node *next; /*结点的指针域*/
}NODE, *LinkList
在链式存储结构中,只需要一个指针(称为头指针,上图中 head)指向第一个结点,就可以顺序地访问到表中的任意一个元素。
在链式存储结构下,进行插入和删除元素,其实实质上都是对相关指针的修改。

插入:
在单链表中,若在 p p p 所指结点后插入新结点 s s s,基本步骤如下:
s->next = p->next;
p->next = s;
我们先将 p p p 所指结点的后继结点指针赋给 s s s 所指结点的指针域,然后将 p p p 所指结点的指针域修改为 s s s 所指结点。
删除:
在单链表中,删除 p p p 所指结点的后继结点时,步骤如下:
q = p->next;
p->next = p->next->next;
free(q)
我们先令临时指针 q q q 指向待删除的结点,然后修改 p p p 所指结点的指针域为指向 p p p 所指向结点的后继的后继结点,从而将元素所在结点从链表中删除,最后释放 q q q 所指结点的空间。
头结点:
在实际应用中,为了简化对链表状态的判定和处理,特别引入一个不存储数据元素的结点,称为头结点,将其作为链表的第一个结点并令头指针指向该结点。
单链表的操作(查找、插入、删除)
单链表的查找操作:
LinkList Find_List(LinkList L, int k) /*L为带头结点单链表的头指针*/
/*在表中查找第k个元素,若找到,返回该元素结点的指针;否则,返回空指针NULL*/
{LinkList p; int i;i = 1; p = L->next; /*初始时,令p指向第一个元素结点,i为计数器*/while(p && i<k) { /*顺指针链向后查找,直到p指向第k个元素结点或p为空指针*/p = p->next; i++;}if(p && i==k) return p; /*存在第k个元素且指针p指向该元素结点*/return NULL
} /*Find_List*/
单链表的插入操作:
int Insert_List(LinkList L, int k, int newElem) /*L为带头结点单链表的头指针*/
/*将元素newElem插入表中的第k个元素之前,若成功则返回0,否则返回-1*/
/*该插入操作等同于将元素newElem插入在第k-1个元素之后*/
{LinkList p,s; /*p,s为临时指针*/if(k == 1) p = L; /*元素newElem要插入到第1个元素之前*/else p = Find_List(L, k-1) /*查找表中的第k-1个元素并令p指向该元素结点*/if(!p) return -1; /*表中不存在第k-1个元素,不满足运算要求*/s = (NODE *)malloc(sizeof(NODE)); /*创建新元素的结点空间*/if(!s) return -1;s->data = newElem;s->next = p->next; p->next = s; /*将元素newElem插入到第k-1个元素之后*/return 0;
} /*Insert_List*/
单链表的删除操作:
int Delete_List(LinkList L, int k) /*L为带头结点的单链表的头指针*/
/*删除表中的第k个元素结点,若成功则返回0,否则返回-1*/
/*删除第k个元素相当于令第k-1个元素结点的指针域指向第k+1个元素所在结点*/
{LinkList p,q; /*p,q为临时指针*/if(k == 1) p = L; /*删除的是第一个元素结点*/else p = Find_List(L, k-1); /*查找表中的第k-1个元素并令p指向该元素结点*/if(!p||!p->next) return -1; /*表中不存在第k个元素*/q = p->next; /*令q指向第k个元素结点*/p->next = q->next; free(q); /*删除结点*/return 0;
} /*Delete_List*/
所以综上,当线性表采用链表作为存储结构时,我们不能对数据元素进行随机访问,但是具有插入和删除操作不需要移动元素的优点。
双向链表
每个结点包含两个指针,分别指向当前元素的直接前驱和直接后继。其特点是可以从表中任意的结点出发,从两个方向上遍历链表。
若双向链表中结点的 front 和 next 指针域分别指示当前结点的直接前驱和直接后继,则在双向链表中插入结点的操作过程表示为:
s->front = p->front;
p->front->next = s;
s->next = p;
p->front = s;

在双向链表中删除结点的操作过程表示为:
p->front->next = p->next;
p->next->front = p->front;
free(p);
循环链表
在单向链表(或双向链表)的基础上令表尾结点的指针指向链表的第一个结点,构成循环链表。其特点是可以从表中任意结点开始遍历整个链表。
静态链表
借助数组来描述线性表的链式存储结构,用数组元素的下标表示元素所在结点的指针。
相关文章:

【软考设计师】S01 数据结构 E01 线性结构 P01 线性表
线性表 前言——线性结构线性表线性表的定义线性表的特点线性表的存储结构顺序存储链式存储单链表双向链表循环链表静态链表 前言——线性结构 线性结构是一种基本的数据结构,主要用于对客观世界中具有单一前驱和后继的数据关系进行描述。线性结构的特点是数据元素…...

nginx配置https 访问
nginx 解压目录有configure文件 [rootoracledb10 ~]# which nginx1、检查nginx是否包含http_ssl_module 模块 如果出现 --with-http_ssl_module 就是已经安装了[rootoracledb10 sbin]# pwd /usr/local/nginx/sbin [rootoracledb10 sbin]# nginx -V nginx version: nginx/1.23…...

希亦CG声波清洗机:眼镜党福利,家庭必备清洗机
对于眼镜党来说最大的烦恼就是每天的佩戴和清洗,清洗是至关重要的,错误的清洗很容易引起镜片损坏,个人一直使用眼镜布清洗,除了费时费力之外清洁度也无法保证。希亦CG声波清洗机正是为了解决这一难题应运而生,可以彻底…...

2023年10月12日历史上的今天大事件早读
公元前539年10月12日波斯国王大流士的军队攻克巴比伦 1492年10月12日西班牙独立日 1492年10月12日哥伦布“发现新大陆” 1773年10月12日法国天文学家梅西叶首次发现具有螺旋结构的星系 1885年10月12日清政府改台湾府为行省 命刘铭传为台湾巡抚 1929年10月12日苏军向张学良…...
uCOSIII实时操作系统 五 任务API(时间片轮转API调度)
时间片轮转调度 时间片轮转法:主要用于分时系统中的进程调度。为了实现轮转调度,系统把所有就绪进程按照先入先出的原则排成一个队列的队首进程,让CPU上运行一个时间片的时间。时间片是一个小小的时间单位,通常为5~10ms数量级。当进程用完分…...

微信小程序项目如何用Hbuild启动,先让对方在微信开发平台将你的微信号添加成开发成员。
微信小程序项目如何用Hbuild启动,先让对方在微信开发平台将你的微信号添加成开发成员。然后在Hbuild官网下载,下载好后运行,点击文件导入项目,然后点击运行,模拟微信小程序,选择微信开发工具的地址…...
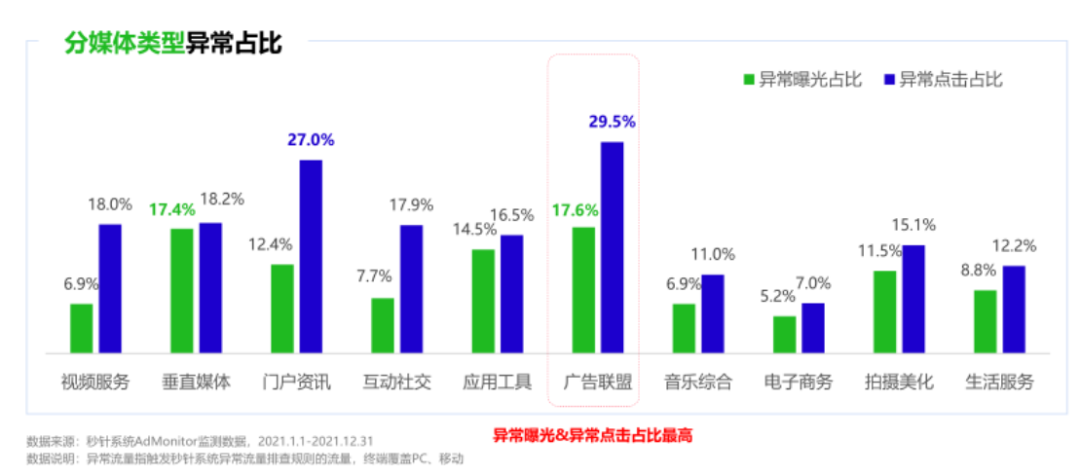
应对广告虚假流量,app广告变现该如何风控?
移动广告市场中的虚假流量一直是困扰各移动应用厂商的难题,广告作为app商业化变现最为直接快捷的途径,也引申出了流量作弊与反作弊的纷争。 根据《2021中国异常流量报告》,2021年中国品牌广告市场因异常流量造成的损失约为326亿人民币&#…...

【算法-动态规划】贝尔曼福特算法
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...
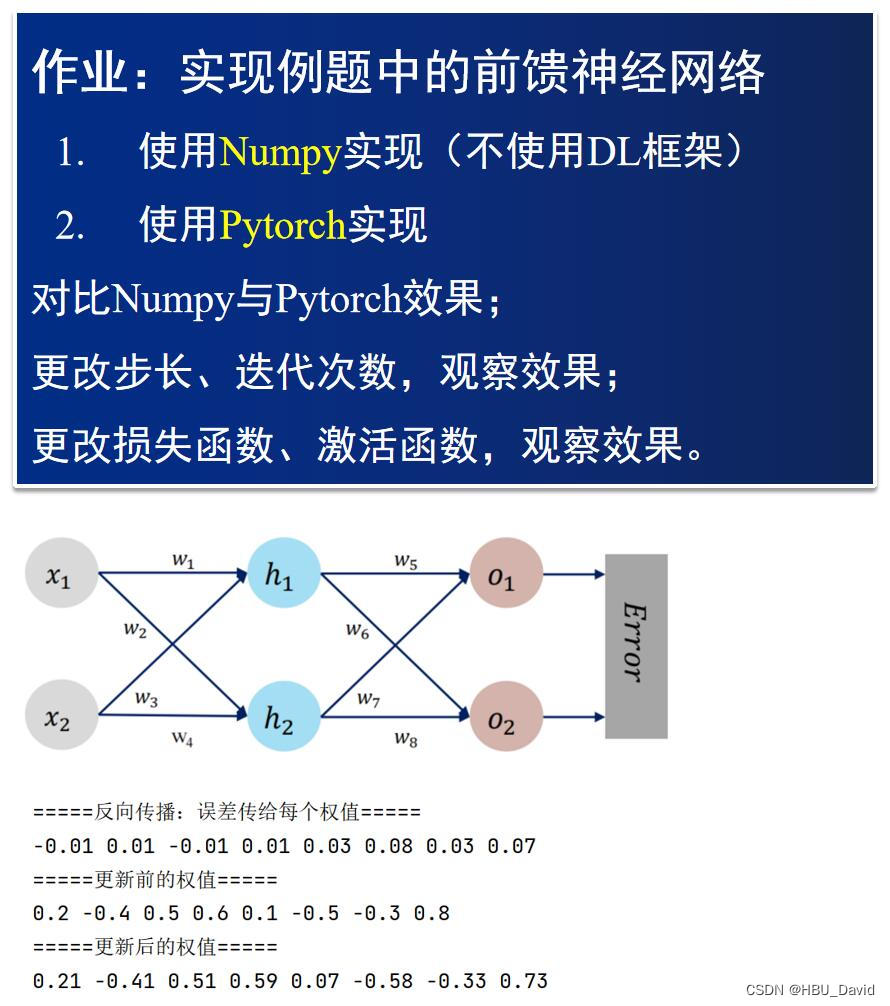
【23-24 秋学期】NNDL 作业3
过程推导 - 了解BP原理数值计算 - 手动计算,掌握细节代码实现 - numpy手推 pytorch自动 对比【numpy】和【pytorch】程序,总结并陈述。激活函数Sigmoid用PyTorch自带函数torch.sigmoid(),观察、总结并陈述。激活函数Sigmoid改变为Relu&#…...
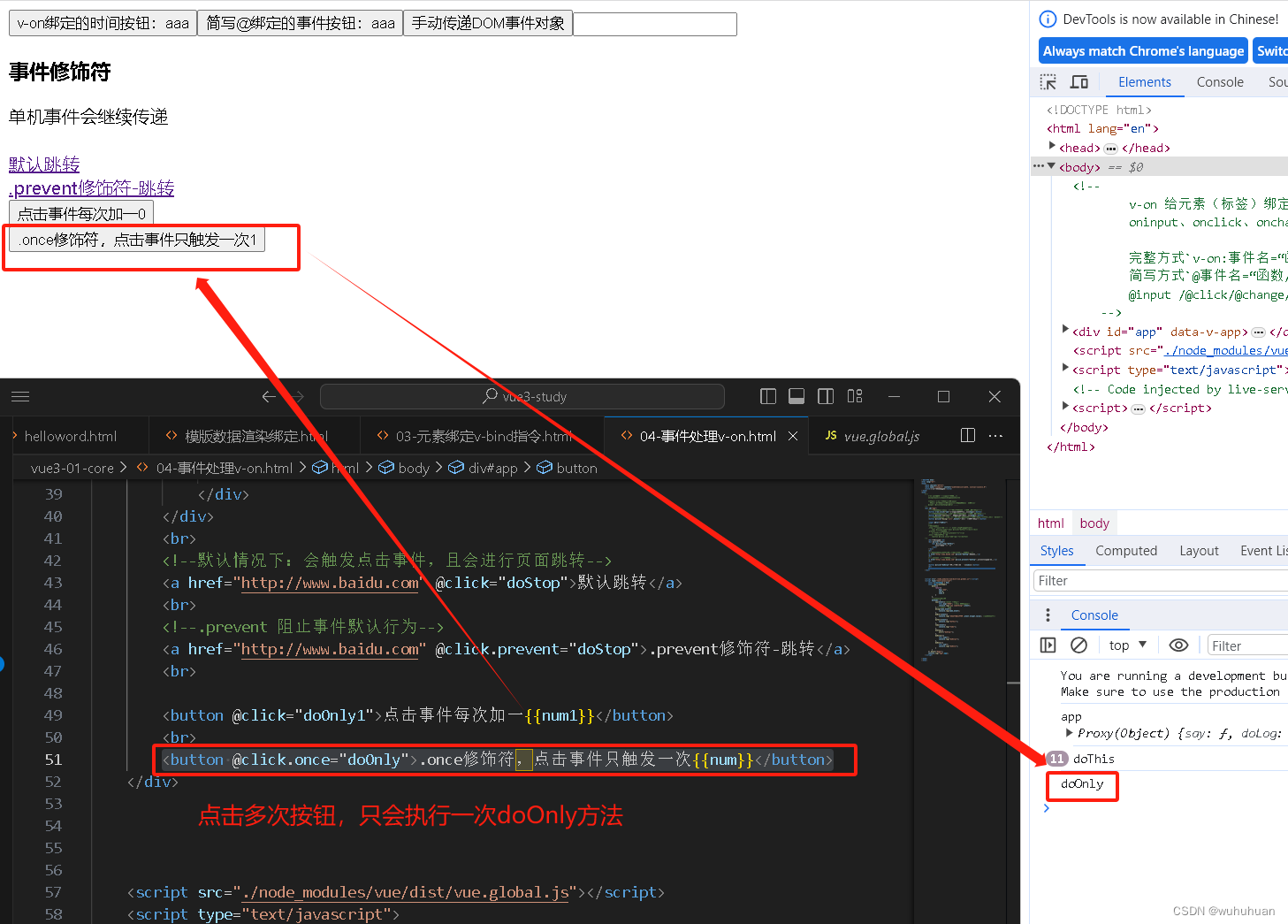
v-on/@ 事件处理指令修饰符-stop、prevent、once
v-on/事件修饰符: 一、.stop 阻止单机事件继续传播 event.stopProgagetion() eg: <h3>事件修饰符</h3> <div click"todo"> <div click.stop"doThis"> 单机事件会继续传递 </div> </div> 点击 单机事…...
macOS Sonoma 14.1beta3(23B5067a)发布
黑果魏叔10 月 11 日消息,苹果今日向 Mac 电脑用户推送了 macOS 14.1 开发者预览版 Beta 3 更新(内部版本号:23B5067a),本次更新距离上次发布隔了 7 天。 根据官方发布的macOS Sonoma 14.1beta3更新日志,此…...

这些负载均衡都解决哪些问题?服务、网关、NGINX?
在微服务项目中,有服务的负载均衡、网关的负载均衡、Nginx的负载均衡,这几个负载均衡分别用来解决什么问题呢? 一、服务的负载均衡 先抛出一个问题: 当一个微服务被多个实例部署时,如何分配和平衡请求的负载&#x…...

#力扣:344. 反转字符串@FDDLC
344. 反转字符串 一、Java class Solution {public void reverseString(char[] s) {for (int l 0, r s.length - 1; l < r; l, r--) {s[l] ^ s[r];s[r] ^ s[l];s[l] ^ s[r];}} } 二、C #include <vector> using namespace std; class Solution { public:void re…...
浅谈SSL通配符证书优势
在当今数字化时代,网络安全是一个日益重要的问题。随着越来越多的网站和应用程序被创建和部署,用户输入的敏感信息面临着潜在的风险。为了确保数据传输的机密性和完整性,SSL(Secure Sockets Layer)证书成为保护用户隐私…...
[开源]基于流程编排的自动化测试工具,插件驱动,测试无限可能
一、开源项目简介 流程编排,插件驱动,测试无限可能 一款基于流程编排的自动化测试工具 二、开源协议 使用Apache-2.0开源协议 三、界面展示 四、功能概述 在软件开发旅程中,测试流程的管理和执行常常是复杂且耗时的挑战。传统测试工具主…...

gdb的一些常见命令收录
gdb的一些常见命令收录 基本命令设置和查看调试其他 基本命令 run 运行程序。 next (n) 单步调试(不进入函数)。 step (s) 单步调试(进入函数)。 continue © 继续执行程序。 quit (q) 退出GDB。 help 获取GDB命令的帮…...

聚观早报 | 首个“5G-A智慧家庭”发布;李鹏称5G-A是5G发展选择
【聚观365】10月12日消息 首个“5G-A智慧家庭”发布 李鹏称5G-A是5G发展的自然选择 新版努比亚Z50S Pro开售 英特尔锐炫A580显卡全球同步上市 vivo X100系列年底登场 首个“5G-A智慧家庭”发布 在全球移动宽带论坛(MBBF2023)期间,du联合…...

golang JWT原理介绍
JWT认证机制 官方文档 JWT文档 原理简介 客户端通过服务端认证之后,由服务端返回一个JSON对象,发回到客户端。客户端保存该对象用于以后服务器访问凭据,服务端完全依赖该JSON对象来验证客户端的身份。由于JSON数据容易被篡改,…...

xcode打包macos报错:FlutterInputs.xcfilelist 和 FlutterOutputs.xcfilelist
xcode 打包macos的时候,报错如下: Unable to load contents of the file list: ‘macos/ephemeral/FlutterInputs.xcfilelist’ ‘macos/ephemeral/FlutterOutputs.xcfilelist’ 解决方案: 我的项目macos下没有找到FlutterInputs.xcfilelis…...

智能机场系统:打造出行体验的未来
随着航空业的迅猛发展,机场作为出行的重要枢纽,必须不断提升自身的服务质量和效率。智能机场系统应运而生,为旅客提供更加便捷、智能化的出行体验。本文将从技术应用、服务优化和安全保障三个方面,全面介绍智能机场系统的特点和优…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
