使用Python构造VARIMA模型
简介
VARMA(p,q)结合了VAR和VMA模型,其中p是向量自回归(VAR)模型的滞后期数,q是VMA模型的移动平均的阶数。
VARMA是ARMA的推广,它将ARMA模型扩展到多个时间序列变量的情况,通过VAR和VMA的线性组合来描述多个时间序列变量之间的联合变化,适合描述多个时间序列变量之间的关系。 时间序列变量。
通过将 q 参数设置为 0,VARMA 模型可以像 VAR 模型一样工作;通过将 p 参数设置为 0,它也可以像 VMA 模型一样工作。VARMA 也不能处理非平稳金融时间序列数据。 矢量自回归积分移动平均(VARIMA)是一种经历差分过程的VARMA模型。
首先,应用约翰森检验(Johansen test ),结果表明英国的GDP、失业率和CPIH之间存在长期均衡关系。
因此,它们可以作为协变量来预测GDP。 正如ARIMA模型分析中提到的,GDP时间序列是不稳定的,因此必须在时间序列中实施一阶差分。 然后,还应用归一化过程。使用 MinMaxScaler() 函数后,数据将缩放到特定范围。 然后,将归一化后的数据按比例划分为训练集和测试集。
通过使用VARMAX功能,它将能够自动与AIC标准进行比较并找到最佳模型。 最优模型将具有最小的 AIC 值。 此外,预测的GDP值需要进行非标准化处理,以便与原始数据进行比较。
代码构建
首先导入需要用到的Python包:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.statespace.varmax import VARMAX
from sklearn.preprocessing import MinMaxScaler
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error然后读取.csv文件的时序数据,这里使用了英国的GDP数据,CPI(通货膨胀率)和Unemployment rate(失业率)作为covariate(协变量)。
# 1. 读取csv时序数据
gdp_data = pd.read_csv('datasets/UK_GDP.csv')[["GDP"]]
inflation_data = pd.read_csv('datasets/UK_inflation.csv')[["Inflation"]]
unemployment_data = pd.read_csv('datasets/UK_unemployment.csv')[["Unemployment"]]
data_origin = gdp_data.copy()接着对所有数据进行一阶差分,使其稳定(因为之前的博客已经对同数据进行过检测,并确定数据不稳定,所以要进行差分)。
gdp_data = gdp_data.diff().dropna()
inflation_data = inflation_data.diff().dropna()
unemployment_data = unemployment_data.diff().dropna()然后对处理过的数据进行归一化。
scaler1 = MinMaxScaler()
scaled_gdp_data = pd.DataFrame(scaler1.fit_transform(gdp_data), columns=gdp_data.columns, index=gdp_data.index)
scaler2 = MinMaxScaler()
scaled_inflation_data = pd.DataFrame(scaler2.fit_transform(inflation_data), columns=inflation_data.columns, index=inflation_data.index)
scaler3 = MinMaxScaler()
scaled_unemployment_data = pd.DataFrame(scaler3.fit_transform(unemployment_data), columns=unemployment_data.columns, index=unemployment_data.index)然后自动定阶,通过AIC找出最合适的参数。
merged_data = pd.concat([scaled_gdp_data, scaled_inflation_data, scaled_unemployment_data], axis=1)
train_size = int(len(merged_data))-3
train_data, test_data = merged_data[:train_size], merged_data[train_size:]best_aic = np.inf
best_order = None
best_model = None
pq_range = range(2) # 取值范围
for p in pq_range:for q in pq_range:try:model = VARMAX(train_data, order=(p, q))result = model.fit()aic = result.aicif aic < best_aic:best_aic = aicbest_order = (p, q)best_model = resultexcept:continueprint("Best order:", best_order)
print("Best AIC:", best_aic)使用VARIMA模型进行预测,打印预测值和真实值的对比图,并计算模型RMSE和MAPE指标。
gdp_predictions = best_model.forecast(steps=len(test_data))[['GDP']]
gdp_predictions = pd.DataFrame(gdp_predictions, columns=['GDP'], index=test_data.index-1)
gdp_predictions = scaler1.inverse_transform(gdp_predictions)
actual = scaler1.inverse_transform(test_data[['GDP']])actual = np.array(gdp_data[-3:].cumsum() + data_origin.values[127])
predictions = gdp_predictions.cumsum() + data_origin.values[127]plt.figure()
plt.plot(actual, label='Actual')
plt.plot(predictions, label='Predicted')
plt.legend()
plt.show()rmse = np.sqrt(mean_squared_error(actual, predictions))
mape = mean_absolute_percentage_error(actual, predictions)
print(f"RMSE: {rmse}")
print(f"MAPE: {mape}")相关文章:

使用Python构造VARIMA模型
简介 VARMA(p,q)结合了VAR和VMA模型,其中p是向量自回归(VAR)模型的滞后期数,q是VMA模型的移动平均的阶数。 VARMA是ARMA的推广,它将ARMA模型扩展到多个时间序列变量的情况,通过VAR和VMA的线性组合来描述多个时间序列变量之间的联…...
Java基于SpringBoot+Vue的考研资讯平台
1 简介 大家好,我是程序员徐师兄,今天为大家带来的是Java基于SpringBootVue的考研资讯平台 Java基于SpringBoot的考研资讯平台,在系统当中学生可以根据不同的信息来实现该网站的考研资讯平台信息的管理。 系统主要分为前台和后台。主要包括…...

信钰证券:9月以来A股20家银行 获机构不同批次调研
Wind数据显现,自9月份以来,已经有20家银行获安排不同批次调研。其间常熟银行、瑞丰银行被调研次数较多,别离为20次、11次;宁波银行、渝农商行获安排调研家数居前,别离为206家、128家。从上市银行宣布的调研情况来看&am…...

应用商店优化的好处有哪些?
应用程序优化优势包括应用在商店的可见性和曝光度,高质量和被相关用户的更好发现,增加的应用下载量,降低用户获取成本和持续增长,增加应用收入和转化率以及全球受众范围。 1、提高知名度并在应用商店中脱颖而出。 如果用户找不到…...
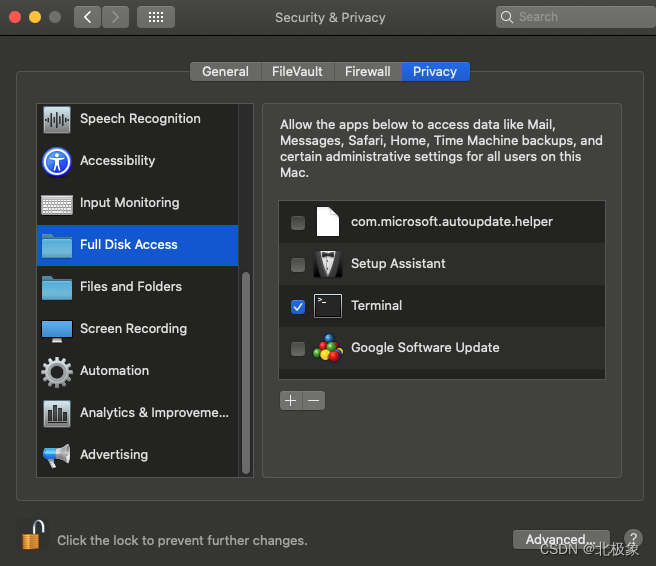
MacOS Pro笔记本硬盘升级纪实
背景 MacPro 2015 mid的苹果本,忽然心血来潮想升级一下SSD。三个步骤:做启动盘,时间机器备份,插新的SSD盘恢复。 过程 下载MacOS,macOS Monterey 12.7官方原版镜像: https://swcdn.apple.com/content/do…...

景联文科技:3D点云标注应用场景和专业平台
3D点云技术之所以得到广泛发展和应用,主要是因为它能够以一种直观、真实和全面的方式来表示和获取现实世界中的三维信息。 3D点云的优势: 真实感和立体感:3D点云数据能够呈现物体的真实感和立体感,使观察者能够更直观地理解物体的…...

基于R语言的水文、水环境模型优化技术及快速率定方法
【阅读原文】:基于R语言的水文、水环境模型优化技术及快速率定方法与多模型案例实践 【内容简介】: 专题一、最速上升法、岭分析以及响应曲面模型 1.最速上升路径 2.信赖域 3.响应面模型 4.二阶响应面 5.岭分析 专题二、Kriging插值与优化方法 …...

学习网络安全得多少费用?网络安全入门了解
前言 网络安全是指对网络系统、硬件、软件和系统数据的保护。不因偶然或者其它原因导致破坏、更改和数据泄露情况。确保网络安全,防止网站被攻击、系统被病毒感染等。随着网络的快速发展,越来越多的用户和公司认识到网络安全的重要性,许多人…...
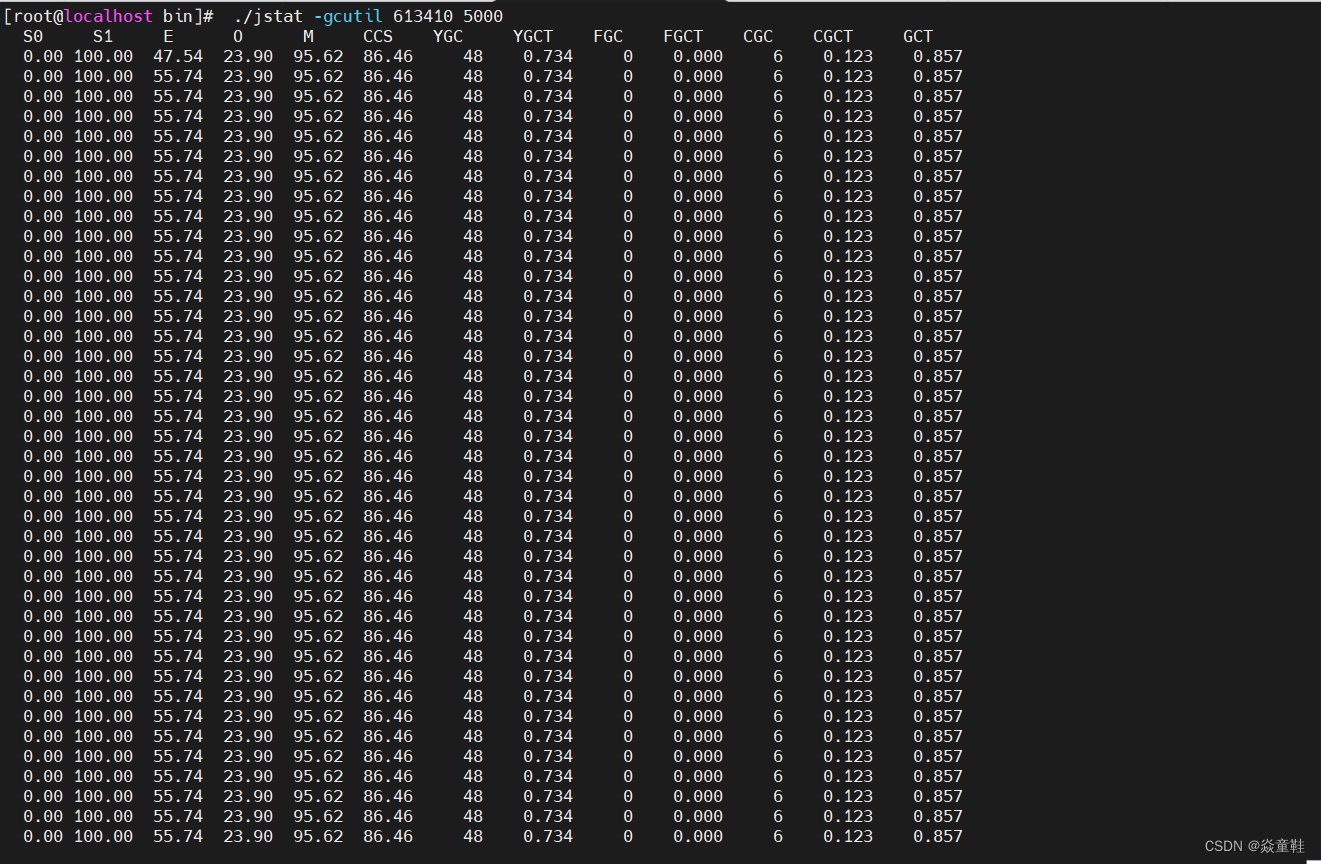
记录一次线上fullgc问题排查过程
某天,接到测试部门反馈说线上项目突然很快,由于当前版本代码和上一版本相比就多了一个刚上线了一个5分钟1次的跑批任务,先关闭次任务后观察是否卡顿,并检查堆内存是否使用完造成频繁gc 1.通过jmap命令查看堆内存中的对象 2.生成当…...

设计接口应该考虑的因素以及遵循的原则
设计接口应该考虑的因素: 接口的业务定位 接口的安全性 接口的可扩展性 接口的稳定性 接口的跨域性 接口的协议规则 接口的路径规则 接口单一原则 接口过滤及接口组合 1.职责原则 在设计接口时,必须明确接口的职责,即接口类型&…...
【产品】智能结构仿真软件AIFEM 2023R2新版本功能介绍
AIFEM是由天洑自主研发的一款通用的智能结构仿真软件,助力用户解决固体结构相关的静力学、动力学、振动、热力学等实际工程问题,软件提供高效的前后处理工具和高精度的有限元求解器,帮助用户快速、深入地评估结构的力学性能,加速产…...

探索数据库的世界:DB、DBMS、DBA、DBS的全面介绍
目录 DB数据库(Database) DBMS数据库管理系统(Database Management System): DBA数据库管理员(Database Administrator): DBS数据库系统(Database System) 总结: DB数据库(Database) 概念: 存储数据的集合,DB可以包含各种类型的数据,文…...

【JVM】初步认识Java虚拟机
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaEE 操作系统 Redis 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 JVM 一、初识JVM1.1 什么是JVM1.2 JVM的功能…...

JAVA设计模式-模板模式
一.概念 定义一个操作中的算法的骨架,而将一些步骤延迟到子类中。模板方法使得子类可以不改变一个算法的结构即可重定义该算法的某些特定步骤。 使用了JAVA的继承机制,在抽象类中定义一个模板方法,该方法引用了若干个抽象方法࿰…...

day007
删除链表第n个节点 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 /*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val …...

Spring Boot项目在Windows上的自启动策略与Windows自动登录配置
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

mac 版hadoop3.2.4 解决 Unable to load native-hadoop library 缺失文件
mac 版hadoop3.2.4或其他版本 Unable to load native-hadoop library 缺失文件 Native 包报错缺失: 1. hadoop-3.2.4/lib/native里加*.dylib 2. hadoop-3.2.4/etc/hadoop/hadoop-env.sh 加或修改 export HADOOP_OPTS"-Djava.library.path/Users/lvan/Documen…...
mysql case when 不命中缓存
case when 在sql 中非常方便数据不同维度统计,但是也会出现mysql 索引不命中问题,当多个case 出现时,需要提取出来到where里面优化 优化后 SELECT date(RecordTime) AS date, count( DISTINCT CASE WHEN Param 1 …...
2023年金九银十网络安全考试试题
2023年金九银十网络安全考试试题 1.关于数据使用说法错误的是: A.在知识分享、案例中如涉及客户网络数据,应取敏感化,不得直接使用 B.在公开场合、公共媒体等谈论、传播或发布客户网络中的数据,需获得客户书面授权或取敏感化,公开…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...