代码随想录算法训练营第五十九天 |647. 回文子串、516.最长回文子序列、动态规划总结篇
一、647. 回文子串
题目链接/文章讲解:代码随想录
思考:
1.确定dp数组(dp table)以及下标的含义
如果本题定义dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话:
会发现很难找到递归关系,dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系,因此本题要从回文字符串的性质着手。
可以找到一种递归关系:
也就是判断一个子字符串(字符串的下表范围[i,j])是否回文,依赖于,子字符串(下表范围[i + 1, j - 1])) 是否是回文,为了明确这种递归关系,dp数组要定义成一位二维dp数组
bool dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
2.确定递推公式
整体上是两种情况,就是s[i]与s[j]相等、不相等:
当s[i] = s[j],dp[i][j] = false。
当s[i] != s[j],有如下三种情况
- 情况一:下标i 与 j相同,是同一个字符例如a,是回文子串
- 情况二:下标i 与 j相差为1,例如aa,也是回文子串
- 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,要看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
if (s[i] == s[j]) {if (j - i <= 1) { // 情况一 和 情况二result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { // 情况三result++;dp[i][j] = true;} }3.dp数组的初始化
dp[i][j]初始化为false
4.确定遍历顺序
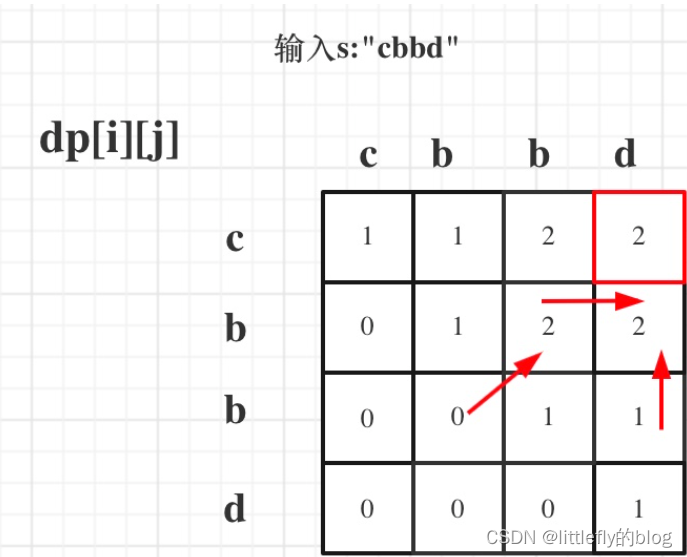
从递推公式中可以看出,情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的。dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:
从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。
for (int i = s.size() - 1; i >= 0; i--) { for (int j = i; j < s.size(); j++) {5.举例推导dp数组
代码实现:
class Solution {
public:int countSubstrings(string s) {vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int result = 0;for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序for (int j = i; j < s.size(); j++) {if (s[i] == s[j]) {if (j - i <= 1) { // 情况一 和 情况二result++;dp[i][j] = true;} else if (dp[i + 1][j - 1]) { // 情况三result++;dp[i][j] = true;}}}}return result;}
};- 时间复杂度:O(n^2)
- 空间复杂度:O(n^2)
二、516.最长回文子序列
题目链接/文章讲解:代码随想录
思考:本题和回文子串思路其实差不多,但比求回文子串简单一点,因为情况少了一点
1.确定dp数组(dp table)以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
2.确定递推公式
如果s[i]与s[j]相同,dp[i][j] = dp[i + 1][j - 1] + 2;
如果s[i]与s[j]不相同,dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
不相同说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2; } else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); }3.dp数组的初始化
从递推公式:dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况,所以需要手动初始化一下,当i与j相同,那么dp[i][j]等于1,其他情况dp[i][j]初始为0
vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0)); for (int i = 0; i < s.size(); i++) dp[i][i] = 1;4.确定遍历顺序
dp[i][j] 依赖于 dp[i + 1][j - 1] ,dp[i + 1][j] 和 dp[i][j - 1]
所以遍历i的时候一定要从下到上遍历,j可以正常从左向右遍历。
for (int i = s.size() - 1; i >= 0; i--) {for (int j = i + 1; j < s.size(); j++) {if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;} else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}} }5.举例推导dp数组
代码实现:
class Solution {
public:int longestPalindromeSubseq(string s) {vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));for (int i = 0; i < s.size(); i++) dp[i][i] = 1;for (int i = s.size() - 1; i >= 0; i--) {for (int j = i + 1; j < s.size(); j++) {if (s[i] == s[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;} else {dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}}return dp[0][s.size() - 1];}
};- 时间复杂度: O(n^2)
- 空间复杂度: O(n^2)
三、动态规划总结篇
题目链接/文章讲解:代码随想录
相关文章:
代码随想录算法训练营第五十九天 |647. 回文子串、516.最长回文子序列、动态规划总结篇
一、647. 回文子串 题目链接/文章讲解:代码随想录 思考: 1.确定dp数组(dp table)以及下标的含义 如果本题定义dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话: 会发现很难找到递归关系,dp[i] 和 dp[i-1]…...

互联网性能和可用性优化CDN和DNS
当涉及到互联网性能和可用性优化时,DNS(Domain Name System)和CDN(Content Delivery Network)是两个至关重要的元素。它们各自发挥着关键作用,以确保用户能够快速、可靠地访问网站和应用程序。在本文中&…...

使用 ErrorStack 在出现报错 ORA-14402 时产生的日志量
0、测试结论: 测试结果:设置 ErrorStack 级别为 1 时产生 Trace 的日志量最小,大小为 308K,同时在 alert 日志中也存在记录。 1、准备测试数据: sqlplus / as sysdba show pdbs alter session set containerpdb; …...

详解Spring-ApplicationContext
加载器目前有两种选择:ContextLoaderListener和ContextLoaderServlet。 这两者在功能上完全等同,只是一个是基于Servlet2.3版本中新引入的Listener接口实现,而另一个基于Servlet接口实现。开发中可根据目标Web容器的实际情况进行选择。 配…...

关键字extern、static与const
关键字extern、static与const extern关键字与include的区别 extern:于声明某个函数或变量是外部的(其他源文件中)include:用于批量引入 项目中可以根据需要引入的函数或变量数量决定使用extern还是include static关键字 static关键字用于限制函数和全局变量的作用域仅在当…...

虹科方案|国庆出游季,古建筑振动监测让历史古迹不再受损
全文导读: 国庆长假即将到来,各位小伙伴是不是都做好了出游计划呢?今年中秋、国庆“双节”连休八天,多地预计游客接待量将创下新高,而各地的名胜古迹更是人流爆满。迎接游客的同时,如何保障历史古迹不因巨大…...

Python学习笔记-使用哈希算法Hash,Hashlib进行数据加密
文章目录 一、概述1.1 哈希算法1.2 常见算法分类1.2.1 SHA算法1.2.2 MD4算法1.2.3 MD5算法 1.3 Hash算法的特性1.4 Hash算法的应用场景1.4.1 数据校验1.4.2 安全加密1.4.3 数字签名 二、Hash算法使用2.1 使用hash函数直接获取hash值2.2 使用hashlib库进行hash计算2.2.1 基本使用…...

跨境电商能否成为黄河流域产业带的新引擎?
近年来,随着全球贸易格局的不断演变和中国经济的快速崛起,跨境电商已经成为中国外贸的一大亮点。而在中国国内,黄河流域产业带一直以其丰富的资源和悠久的历史而闻名,但也面临着转型升级的挑战。那么,跨境电商是否有潜…...
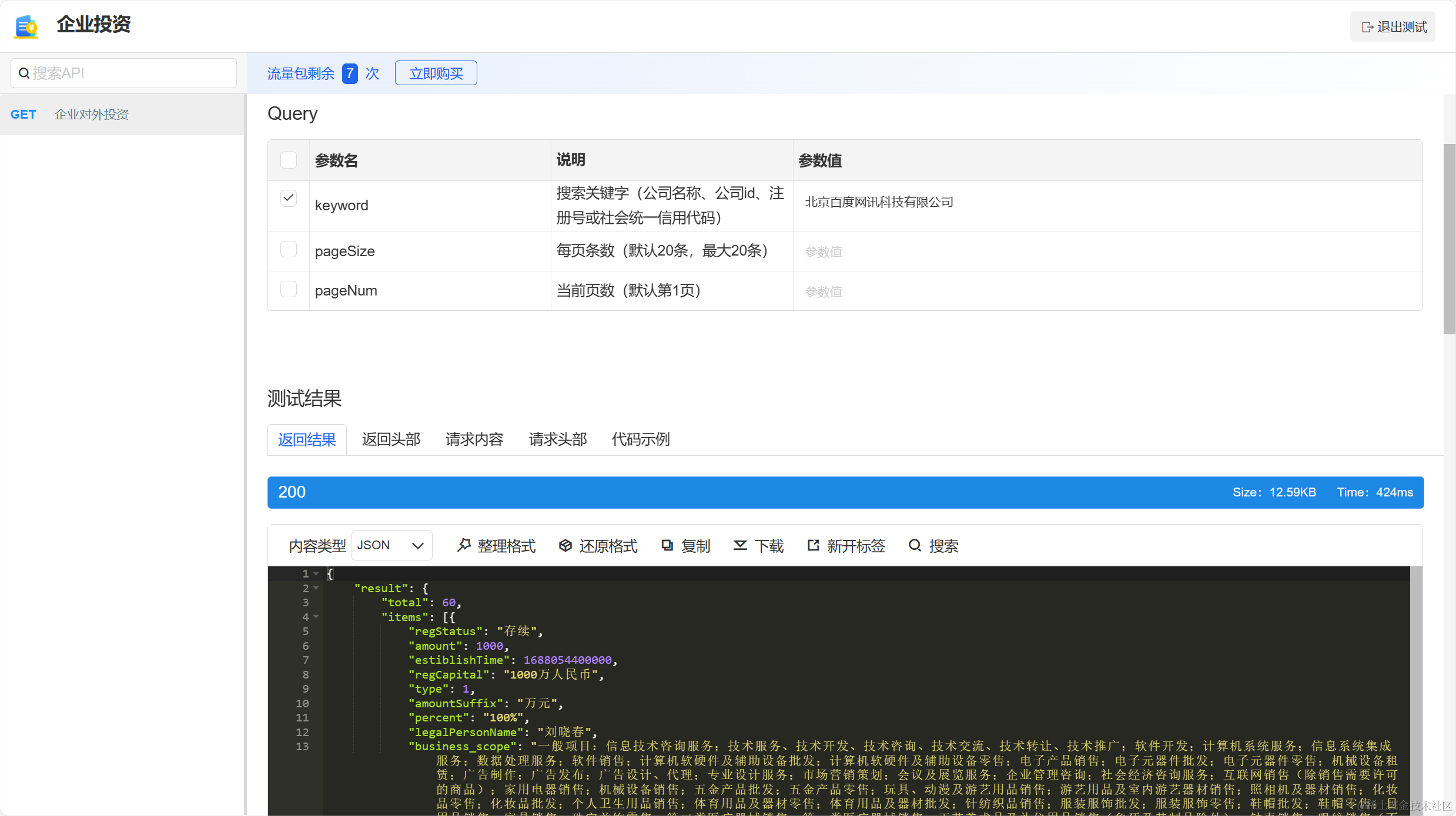
从数据到决策:企业投资信息查询API的关键作用
前言 在现代商业环境中,数据是一项无价的资产。企业不仅需要访问大量数据,还需要将这些数据转化为有用的见解,以支持战略决策。对于企业投资而言,准确的信息和实时的市场数据至关重要。在这个信息时代,企业投资信息查…...
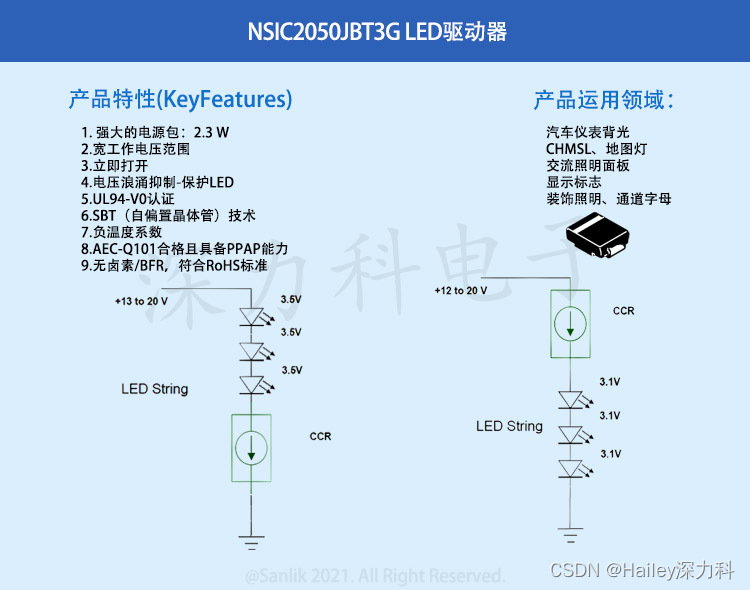
NSIC2050JBT3G 车规级120V 50mA ±15% 用于LED照明的线性恒流调节器(CCR) 增强汽车安全
随着汽车行业的巨大变革,高品质的汽车氛围灯效、仪表盘等LED指示灯效已成为汽车内饰设计中不可或缺的元素。深力科安森美LED驱动芯片系列赋能智能座舱灯效充满艺术感和科技感——NSIC2050JBT3G LED驱动芯片,实现对每路LED亮度和颜色进行细腻控制…...
-- ftp - ftp 客户端)
LuatOS-SOC接口文档(air780E)-- ftp - ftp 客户端
ftp.login(adapter,ip_addr,port,username,password)# FTP客户端 参数 传入值类型 解释 int 适配器序号, 只能是socket.ETH0, socket.STA, socket.AP,如果不填,会选择平台自带的方式,然后是最后一个注册的适配器 string ip_addr 地址 string port 端口,默认21 string…...

第二证券:市净率高好还是低好?
市净率是一个衡量公司股票投资价值的指标,通过比较公司股票价格和公司每股净资产的比值来评估公司股票的估值水平。市净率高好还是低好这个问题并没有一个简单的答案,取决于具体的市场环境和投资者的需求。本文将从多个角度分析市净率高好还是低好。 首…...
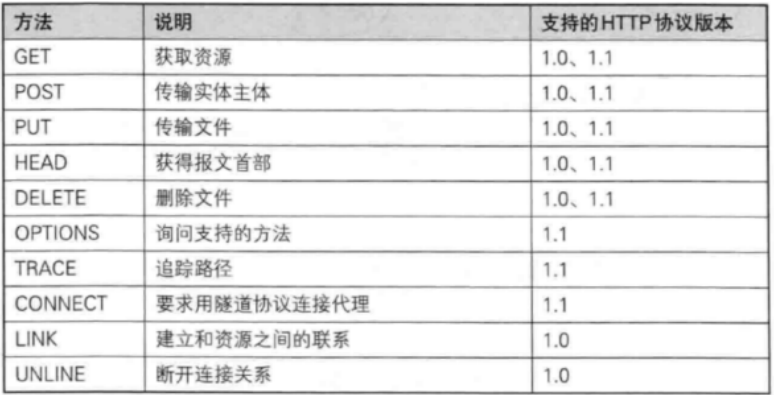
HTTP协议是什么
HTTP (全称为 “超文本传输协议”) 是一种应用非常广泛的 应用层协议,是一种网络通信协议。 超文本:所谓 “超文本” 的含义, 就是传输的内容不仅仅是文本(比如 html, css 这个就是文本), 还可以是一些其他的资源, 比如图片, 视频, 音频等二进制的数据。…...
微服务09-Sentinel的入门
文章目录 微服务中的雪崩现象解决办法:1. 超时处理2. 舱壁模式3. 熔断降级4.流量控制 Sentinel1.介绍2.使用操作3.限流规则4.实战:流量监控5.高级选项功能的使用1.关联模式2.链路模式3.总结 流控效果1.预热模式2.排队等待模式3.总结4.热点参数限流5.实战…...
2023-2024-1 高级语言程序设计实验一: 选择结构
7-1 古时年龄称谓知多少? 输入一个人的年龄(岁),判断出他属于哪个年龄段 ? 0-9 :垂髫之年; 10-19: 志学之年; 20-29 :弱冠之年; 30-39 &#…...
js事件循环详解
事件循环简介 JavaScript的事件循环是一种处理异步事件和回调函数的机制,它是在浏览器或Node.js环境中运行,用于管理任务队列和调用栈,以及在适当的时候执行回调函数。 事件循环的基本原理是,JavaScript引擎在空闲时等待事件的到…...
实战指南:使用 kube-prometheus-stack 监控 K3s 集群
作者简介 王海龙,Rancher 中国社区技术经理,Linux Foundation APAC Evangelist,负责 Rancher 中国技术社区的维护和运营。拥有 9 年的云计算领域经验,经历了 OpenStack 到 Kubernetes 的技术变革,无论底层操作系统 Lin…...

golang调用scws实现简易中文分词
1、安装 scws 官网以及文档 https://github.com/hightman/scws wget -q -O - http://www.xunsearch.com/scws/down/scws-1.2.3.tar.bz2 | tar xjf -cd scws-1.2.3 ./configure --prefix/usr/local/scws --enable-shared make && make installLibraries have been ins…...
Excel 中使用数据透视图进行数据可视化
使用数据透视表(PivotTable)是在Excel中进行数据可视化的强大工具。下面将提供详细的步骤来使用数据透视表进行数据可视化。 **步骤一:准备数据** 首先,确保你有一个包含所需数据的Excel表格。数据应该按照一定的结构和格式组织…...

在SIP 语音呼叫中出现单通时要怎么解决?
在VoIP的环境中,特别是基于SIP通信的环境中,我们经常会遇到一些非常常见的问题,例如,单通,注册问题,回声,单通等。这些问题事实上都有非常直接的排查方式和解决办法,用户可以按照一定…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...


