AM@邻域@极限定义中的符号说明
文章目录
- abstract
- 邻域👺
- 邻域中心和半径
- 去心邻域
- ϵ , δ \epsilon,\delta ϵ,δ的意义
- 各种极限定义的共同点
- 几何意义
- 极限定义中的极限过程临界值
- ϵ \epsilon ϵ的选取👺
- 概念辨析👺
- 无限接近不同于越来越接近
- 例
- 例
- 越来越接近推不出无限接近
abstract
- 邻域的概念
- 极限的定义中的符号说明
邻域👺
- 设 x 0 ∈ R , δ > 0 x_0\in\mathbb{R},\delta\gt0 x0∈R,δ>0,开区间 R δ = ( x 0 − δ , x 0 + δ ) R_\delta=(x_0-\delta,x_0+\delta) Rδ=(x0−δ,x0+δ)称为** x 0 {x_0} x0的 δ \delta δ 邻域**,记作 U ( x 0 , δ ) U(x_0,\delta) U(x0,δ)或 U δ ( x 0 ) U_{\delta}(x_0) Uδ(x0)
- 区间 R δ R_{\delta} Rδ也可以表示为绝对值不等式: ∣ x − x 0 ∣ < δ |x-x_0|<\delta ∣x−x0∣<δ的解集: { x ∣ ∣ x − x 0 ∣ < δ } \set{x||x-x_0|<\delta} {x∣∣x−x0∣<δ}
- 因为 ∣ x − x 0 ∣ < δ |x-x_0|<\delta ∣x−x0∣<δ ⇔ \Leftrightarrow ⇔ − δ < x − x 0 < δ -\delta<x-x_0<\delta −δ<x−x0<δ ⇔ \Leftrightarrow ⇔ x 0 − δ < x < x 0 + δ x_0-\delta<x<x_0+\delta x0−δ<x<x0+δ
- 如果不需要说明 δ \delta δ,可简记为 U ( x 0 ) U(x_0) U(x0)
邻域中心和半径
- x 0 x_0 x0为邻域 U ( x 0 , δ ) U(x_0,\delta) U(x0,δ)的中心,称为邻域中心, δ \delta δ称为邻域半径
去心邻域
- 点 x 0 x_0 x0的去心 δ \delta δ邻域, R δ ˚ R_{\mathring{\delta}} Rδ˚= ( x 0 − δ , x 0 ) ∪ ( x 0 , x 0 + δ ) (x_0-\delta,x_0)\cup(x_0,x_0+\delta) (x0−δ,x0)∪(x0,x0+δ)记作 U ˚ ( x 0 , δ ) \mathring{U}(x_0,\delta) U˚(x0,δ),或 U ˚ δ ( x 0 ) \mathring{U}_{\delta}(x_0) U˚δ(x0)
- 区间 R δ ˚ R_{\mathring{\delta}} Rδ˚也可以表示为: { x ∣ 0 < ∣ x − x 0 ∣ < δ } \set{x|0<|x-x_0|<\delta} {x∣0<∣x−x0∣<δ}
- 如不需要说明 δ \delta δ,可简记为 U ˚ ( x 0 ) \mathring{U}(x_0) U˚(x0)
ϵ , δ \epsilon,\delta ϵ,δ的意义
- ϵ \epsilon ϵ是用来刻画 f ( x ) f(x) f(x)与 A A A的接近程度(刻画函数值)
- δ \delta δ是用来刻画 x → x 0 x\to{x_0} x→x0这个极限过程(刻画自变量)
- x → x 0 x\to{x_0} x→x0但 x ≠ x 0 x\neq{x_0} x=x0
- 极限 lim x → x 0 f ( x ) \lim\limits_{x\to{x_0}}f(x) x→x0limf(x)是否存在,若存在极限,极限值等于多少
- 和" x = x 0 x=x_0 x=x0处有没有定义,若有定义函数值等于多少"无关
- 和 x = x 0 x=x_0 x=x0的去心邻域 U ˚ ( x 0 , δ ) \mathring{U}(x_0,\delta) U˚(x0,δ)函数值有关
- 要使 lim x → x 0 f ( x ) \lim\limits_{x\to{x_0}}f(x) x→x0limf(x)存在, f ( x ) f(x) f(x)必须在 x = x 0 x=x_0 x=x0的某去心领域 U ˚ ( x 0 , δ ) \mathring{U}(x_0,\delta) U˚(x0,δ)处处有定义
各种极限定义的共同点
- 无论是数列极限还是函数极限,都用了正数 ϵ \epsilon ϵ来刻画极限存在的形式
- 当 ϵ \epsilon ϵ可以任意取(足够小)的时候,才能够体现极限的意义(它刻画了数列在靠近极限的过程的与极限的接近程度),因此定义中总是强调任意的正数 ϵ \epsilon ϵ( ∀ ϵ > 0 \forall{\epsilon>0} ∀ϵ>0)
几何意义
- 对任意给定的 ϵ > 0 \epsilon>0 ϵ>0,总存在 U ˚ ( x 0 , δ ) \mathring{U}(x_0,\delta) U˚(x0,δ),当 x ∈ U ˚ ( x 0 , δ ) x\in{\mathring{U}(x_0,\delta)} x∈U˚(x0,δ)时,曲线 y = f ( x ) y=f(x) y=f(x)夹在两直线 y = A − ϵ y=A-\epsilon y=A−ϵ,和 y = A + ϵ y=A+\epsilon y=A+ϵ之间
极限定义中的极限过程临界值
- 根据上述极限的定义,数列极限中的 N N N,函数极限中的 X X X或 δ \delta δ,都是给定 ϵ \epsilon ϵ后,构造极限过程的区间(例如 n > N , x > X , 0 < ∣ x − a ∣ < δ n>N,x>X,0<|x-a|<\delta n>N,x>X,0<∣x−a∣<δ)的参数,不妨称之为极限过程临界值
- X X X(或 N N N)和预先给定的 ϵ ( ϵ > 0 ) \epsilon(\epsilon>0) ϵ(ϵ>0)有关,但是 X X X并不是 ϵ \epsilon ϵ的函数
-
因为同一个 ϵ \epsilon ϵ可以对应多个(甚至无穷多个)符合条件的 X X X
-
若 X = X 1 X=X_1 X=X1满足 x > X x>X x>X时 f ( x ) ∈ U ( A , ϵ ) f(x)\in{U(A,\epsilon)} f(x)∈U(A,ϵ),则 X = X 2 ( X 2 > X 1 ) X=X_2(X_2>X_1) X=X2(X2>X1)也满足
-
ϵ \epsilon ϵ的选取👺
- 若 lim x → ∗ f ( x ) = A \lim\limits_{x\to{*}}f(x)=A x→∗limf(x)=A,则 ∀ ϵ > 0 \forall{\epsilon>0} ∀ϵ>0, ∃ δ > 0 \exist{\delta>0} ∃δ>0,当 x ∈ U ( x 0 , δ ) ˚ x\in\mathring{U(x_0,\delta)} x∈U(x0,δ)˚时, ∣ f ( x ) − A ∣ < ϵ |f(x)-A|<\epsilon ∣f(x)−A∣<ϵ
- 在实际应用极限定义作推理的时候,经常时以如下形式出现:
- ∀ ϵ = θ ( c ) > 0 \forall{\epsilon=\theta(c)>0} ∀ϵ=θ(c)>0, ∃ δ > 0 \exist{\delta>0} ∃δ>0,当 x ∈ U ( x 0 , δ ) ˚ x\in\mathring{U(x_0,\delta)} x∈U(x0,δ)˚时, ∣ f ( x ) − A ∣ < ϵ = θ ( c ) |f(x)-A|<\epsilon=\theta(c) ∣f(x)−A∣<ϵ=θ(c)
- 其中 θ ( c ) \theta(c) θ(c)是一个大于0的常数表达式,例如取 θ ( c ) \theta(c) θ(c)为某个常数 M M M或 1 M \frac{1}{M} M1
- 有时也把 ϵ \epsilon ϵ隐去不写,而直接以给定的值 θ ( c ) \theta(c) θ(c)来应用极限的条件
- 因为 f ( x ) → A ( x → ∗ ) f(x)\to{A}(x\to{*}) f(x)→A(x→∗),所以 ϵ = θ ( c ) \epsilon=\theta(c) ϵ=θ(c)可以取任何正数
- 通常, ϵ \epsilon ϵ取值在能够说明问题的前提下,取值越简单,越具体越好(不一定越小越好),可能是
- 极限值 A A A相关的表达式(通常是 A 2 \frac{A}{2} 2A,这种手法可以推导出许多重要结论);
- 具体常数,比如 1 1 1
- ϵ \epsilon ϵ的表达式(例如 ϵ 2 \frac{\epsilon}{2} 2ϵ,而不一定是 ϵ \epsilon ϵ本身,因为 ϵ \epsilon ϵ也是一个正的常数)
- ∀ ϵ = θ ( c ) > 0 \forall{\epsilon=\theta(c)>0} ∀ϵ=θ(c)>0, ∃ δ > 0 \exist{\delta>0} ∃δ>0,当 x ∈ U ( x 0 , δ ) ˚ x\in\mathring{U(x_0,\delta)} x∈U(x0,δ)˚时, ∣ f ( x ) − A ∣ < ϵ = θ ( c ) |f(x)-A|<\epsilon=\theta(c) ∣f(x)−A∣<ϵ=θ(c)
- 例如
- 无穷小之和仍为无穷小的证明中,就是以上述方式运用极限的条件
- 证明函数极限的有界性时,取 ϵ = 1 \epsilon=1 ϵ=1
- 证明函数极限的局部保号性时,可以取 ϵ = ± A 2 \epsilon=\pm\frac{A}{2} ϵ=±2A
概念辨析👺
- 这里要辨析的概念(假设 x → ∗ x\to{*} x→∗的极限过程中)
- 可无限接近(要多接近有多接近)的值是极限
- 越来越接近的值不一定是极限
- 无限接近不同于越来越接近
- 无限接近得不出越来越接近
- 越来越接近也得不出无限接近
无限接近不同于越来越接近
-
无限接近(任意接近)于极限(趋近于极限) ⇎ \not\Leftrightarrow ⇔越来越接近极限
-
极限强调的时无限接近,但不要求严格的越来越接近,只要总体上是越来越接近即可
-
lim x n → ∞ x n = 0 \lim_{x_n\to \infin}x_n=0 limxn→∞xn=0,我们不能够说, x n x_n xn随着 n → ∞ n\to \infin n→∞ , x n ,x_n ,xn越来越接近 x n x_n xn
-
例
-
不单调也可以无限接近(有极限)
-
x n = 1 n x_n=\frac{1}{n} xn=n1;极限 x n = 0 ( n → ∞ ) x_n=0(n\to \infin) xn=0(n→∞)单调而且有极限0
-
x n = ( − 1 ) n n x_n=\frac{(-1)^{n}}{n} xn=n(−1)n= ( − 1 ) n 1 n (-1)^{n}\frac{1}{n} (−1)nn1;极限 x n = 0 ( n → ∞ ) x_n=0(n\to \infin) xn=0(n→∞)不单调但是也有极限0
例
- 令 f 1 ( x ) f_1(x) f1(x)= 1 x \frac{1}{x} x1; f 2 ( x ) f_2(x) f2(x)= 3 x \frac{3}{x} x3; f ( x ) = { f 1 ( x ) ( n 为奇数 ) f 2 ( x ) ( n 为偶数 ) f(x)=\begin{cases} f_1(x)&(n为奇数)\\ f_2(x)&(n为偶数)\end{cases} f(x)={f1(x)f2(x)(n为奇数)(n为偶数)
- f 1 ( x ) f_1(x) f1(x), f 2 ( x ) f_2(x) f2(x)都满足 x n → 0 ( n → ∞ ) x_n\rightarrow0(n\rightarrow\infin) xn→0(n→∞);而 f ( x ) f(x) f(x)是振荡地趋近于0
- x 1 , x 2 , x 3 , x 4 , … x_1,x_2,x_3,x_4,\dots x1,x2,x3,x4,… 分别等于 1 , 3 2 , 1 3 , 3 4 1,\frac{3}{2},\frac{1}{3},\frac{3}{4} 1,23,31,43
越来越接近推不出无限接近
-
y = 1 x + 1 ( x > 0 ) y=\frac{1}{x}+1(x>0) y=x1+1(x>0), x → ∞ x\to \infin x→∞ 的过程越来越接近于 y = 1 y=1 y=1,同时 y y y还越来越接近与 y = 0 y=0 y=0,
-
尽管 y y y可以无限接近于1,但是无法无限接近于 y = 0 y=0 y=0,因为我们可以肯定: y > 1 y>1 y>1;
相关文章:

AM@邻域@极限定义中的符号说明
文章目录 abstract邻域👺邻域中心和半径去心邻域 ϵ , δ \epsilon,\delta ϵ,δ的意义各种极限定义的共同点几何意义极限定义中的极限过程临界值 ϵ \epsilon ϵ的选取👺 概念辨析👺无限接近不同于越来越接近例例 越来越接近推不出无限接近 …...
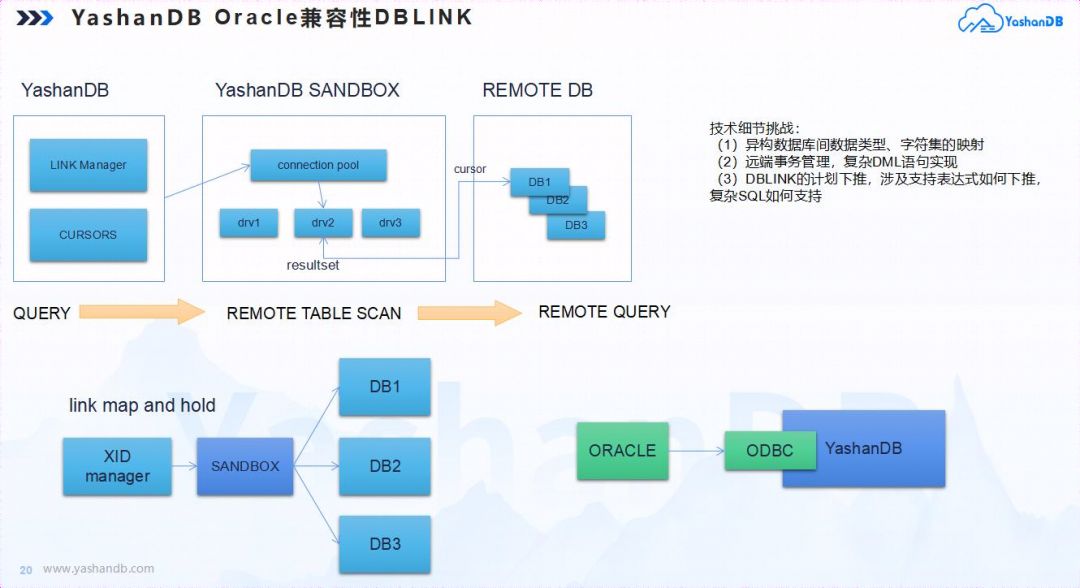
论Oracle兼容性,我们需要做什么
作者介绍:王海峰,数据库系统架构师,YashanDB SQL开发负责人,10年以上数据库内核技术开发经验。 Oracle兼容性是目前国产数据库的关键任务之一,其直接影响到商业迁移的成本和竞争力。 我们经常发现,部分国产…...
你知道多号发圈的同时并延迟评论的方式吗?
你知道多号发圈的同时并延迟评论的方式吗? 其实很简单。 步骤1:编辑好朋友圈内容 步骤2:设置延迟评论 步骤3:选择多个号发圈 通过以上3个步骤,就可以实现多号发圈的同时并延迟评论。 在发布朋友圈前,只需要…...
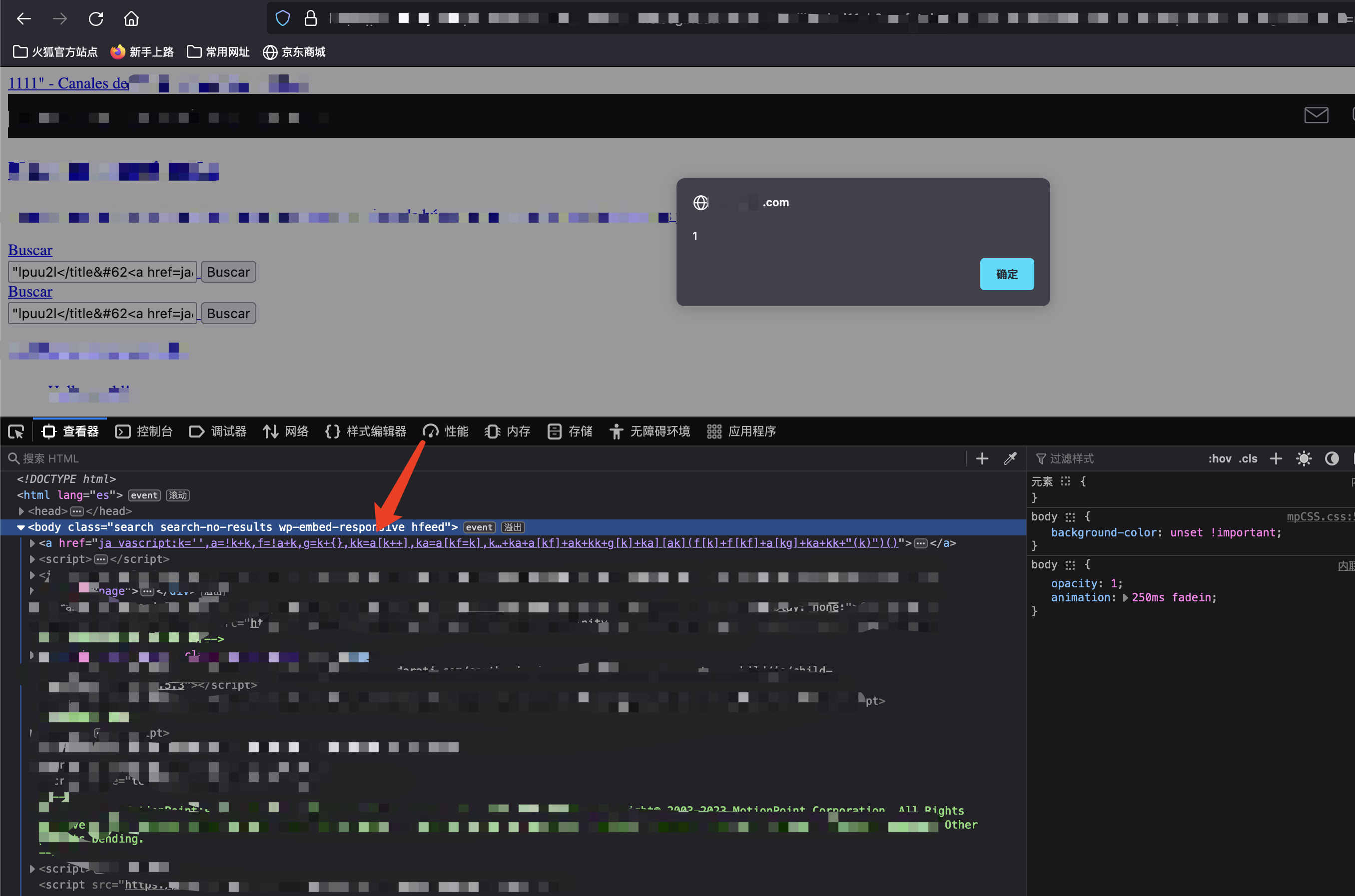
【BugBounty】记一次XSS绕过
前言 最近一直在看国外的赏金平台,绕waf是真的难受, 记录一下绕过的场景。 初步测试 一开始尝试XSS,发现用户的输入在title中展示,那么一般来说就是看能否闭合,我们从下面图中可以看到,输入尖括号后被转成了实体。 …...

Linux文件目录结构详解:根目录和常见子目录介绍
文章目录 引言1. 什么是Linux文件目录结构2. Linux文件系统的重要性 根目录(/)2.1 根目录的作用和特点2.2 根目录下常见目录的介绍 /bin 目录3.1 /bin 目录的作用和内容3.2 常见的可执行命令示例 /etc 目录4.1 /etc 目录的作用和内容4.2 配置文件的存放位…...

知识付费小程序的推广与用户增长策略
在知识付费小程序开发完成后,推广和用户增长是关键的成功因素。本文将探讨一些推广策略和用户增长方法,并提供代码示例,帮助您在知识付费小程序中实施这些策略。 1. 社交媒体分享功能 在知识付费小程序中添加社交媒体分享功能,…...
微信小程序 获取当前屏幕的可见高宽度
很多时候我们做一下逻辑 需要用整个窗口的高度或宽度参与计算 而且很多时候我们js中拿到的单位都是px像素点 没办法和rpx同流合污 官方提供了wx.getSystemInfoSync() 可以获取到部分窗口信息 其中就包括了整个窗口的宽度和高度 wx.getSystemInfoSync().windowHeight 返回值为像…...

使用 Splashtop 驾驭未来媒体和娱乐
在当今时代,数字转型不再是可选项,而是必选项。如今,媒体与娱乐业处于关键时刻,正在错综复杂的创意、技术和远程协作迷宫之中摸索前进。过去几年发生的全球事件影响了我们的日常生活,不可逆转地改变了行业的运作方式&a…...
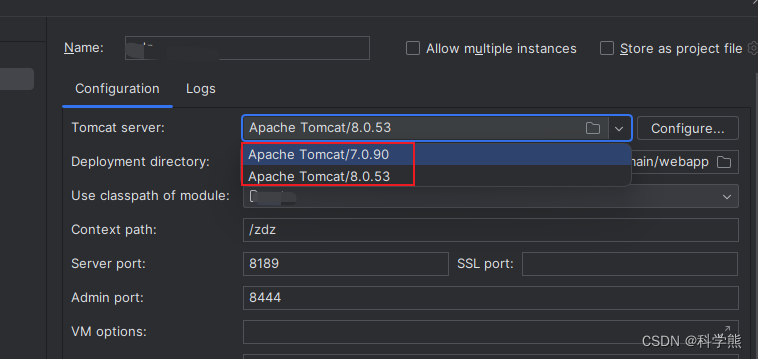
Tomcat项目启动报错
java.io.IOException: java.lang.ClassCastException: Cannot cast org.springframework.web.SpringServletContainerInitializer to javax.servlet.ServletContainerInitializer解决办法:可能Tomcat版本不对,使用7.0.90版本启动报错,使用8.0…...

offer
【录用通知书】 如何判断公司的好坏呢。 注意了,我们软件行业,技术管理类,技术类,产品类 好公司好企业基本都会给你说清楚,一项多少钱,加班多少钱,这样的 像这类公司的薪资结构复杂就要特别…...
漏洞复现--鸿运主动安全监控云平台任意文件下载
免责声明: **文章中涉及的漏洞均已修复,敏感信息均已做打码处理,文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何…...

第二章 物理层 | 计算机网络(谢希仁 第八版)
文章目录 第二章 物理层2.1 物理层的基本概念2.2 数据通信的基础知识2.2.1 数据通信系统的模型2.2.2 有关信道的几个基本概念2.2.3 信道的极限容量 2.3 物理层下面的传输媒体2.3.1 导引型传输媒体2.3.2 非导引型传输媒体 2.4 信道复用技术2.4.1 频分复用、时分复用和统计时分复…...
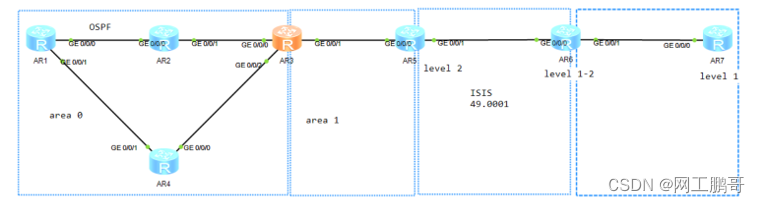
路由高级特性
项目拓扑与项目需求 项目需求 某企业网络使用ospf和isis作为IGP协议实现内部网络的互联互通,区域规划和IP规划如图所示,现在要求实现如下需求: LSW1和AR1使用vlan10互联,与AR2使用vlan20互联,LSW1与LSW2、3、4之间使…...
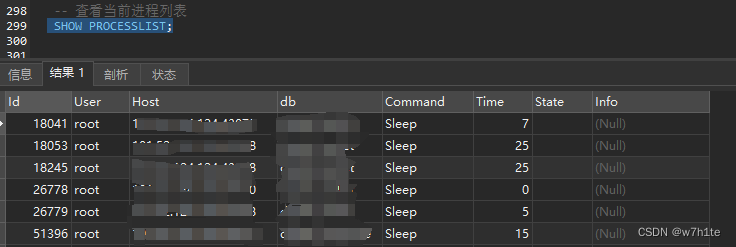
【MySQL】数据库排查慢查询、死锁进程排查、预防以及解决方法
MySQL数据库排查慢查询、死锁进程及解决方法 一、排查慢查询 1.1检查慢查询日志是否开启 1.1.1使用命令检查是否开启慢查询日志: SHOW VARIABLES LIKE slow_query_log;如果是 Value 为 off 则并未开启 1.1.2开启并且查看慢查询日志: MySQL提供了慢查询日志功能,可以记录所…...
WSL2下的Docker配置和使用
在Windows的Linux子系统(Windows Subsystem for Linux)WSL2中安装、配置和使用 Docker,可以参考官方教程:WSL上的Docker远程容器入门. 重要步骤总结如下: 先决条件 确保你的计算机运行的是 Windows 10(更…...
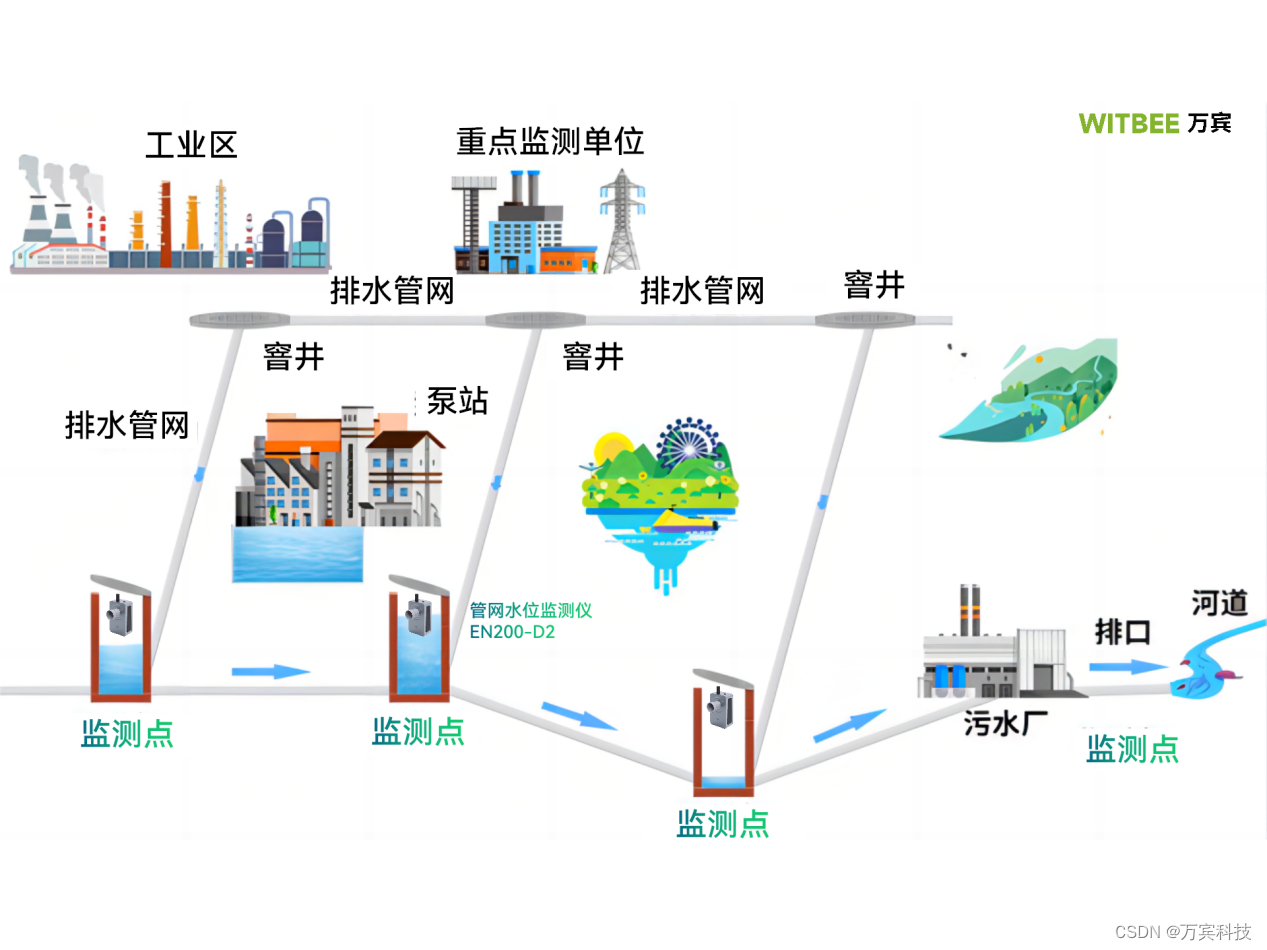
污水管网水位监测,管网水位监测仪守护城市污水管网运行
万宾科技:污水管网水位监测 近年来,城市化进程的加速使得污水管网建设愈发重要。然而,在管网运维中,水位监测一直以来都是一个令人头痛的难题。为了解决这一问题,万宾科技公司推出了管网水位监测仪EN200-D2࿰…...
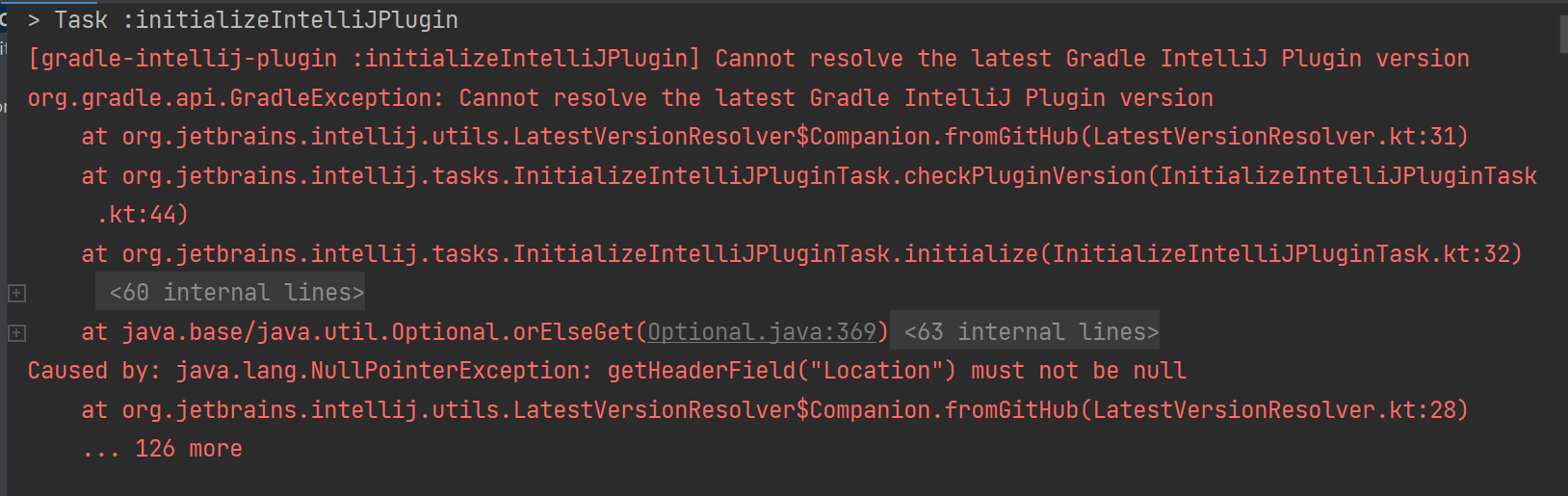
IDEA插件版本升级和兼容新版本idea
1.关于IDEA插件的版本设置问题 打开jetbrains插件市场,随意打开一个插件详情页面的Versions菜单,我们可以看见一个插件包不同时期发布的不同版本(Versions),并且每个版本包含了可兼容IDEA或PyCharm的版本范围…...
Docker 容器应急
容器网络简单理解 容器拥有n多张veth网卡与一张docker0网卡 docker 五种网络 bridge 默认网络,Docker启动后创建一个docker0网桥,默认创建的容器也是添加到这个网桥中。host 容器不会获得一个独立的network namespace,而是与宿主机共用一个…...
webservice接口自动化测试
1,用soupui进行测试 2,安装soupUI 3,测试的时候是给了一个wdsl 操作步诹:new (name , 填写地址)---导入wsdl文件---看到所有的接口 发送请求的格式<xml> canshu</xml> 应用场景,…...

精益生产与MES生产管理系统相互融合
近年来,精益生产理念在企业管理中越来越受欢迎。它强调以最小的浪费,在最短的时间内,生产出高质量的产品。这一理念的实施手段包括准时制生产方式、适时生产方式等,消除浪费、看板、快换工装等都是精益提高的工具方针。 然而&…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
