AM@数列极限
文章目录
- abstract
- 极限👺
- 极限的主要问题
- 数列极限
- 数列极限的定义@ ( ϵ − N ) (\epsilon-N) (ϵ−N)语言描述
- 极限表达式成立的证明
- 极限发散证明
- 常用数列极限
- 数列极限的几何意义
- 例
- 函数的极限
abstract
- 数列极限
极限👺
- 极限分为数列的极限和函数的极限
- 函数的极限又有6种极限过程:形式地记为 x → ∗ x\to{*} x→∗,其中 ∗ * ∗可能是:
- x 0 , x 0 − , x 0 + x_0,x_0^{-},x_0^{+} x0,x0−,x0+
- ∞ , − ∞ , + ∞ \infin,-\infin,+\infin ∞,−∞,+∞
极限的主要问题
- 求给定数列或函数的极限值
- 证明给定数列或函数的极限是某个值(通常用极限的定义法作证明)
数列极限
数列极限的定义@ ( ϵ − N ) (\epsilon-N) (ϵ−N)语言描述
- 若对任何的 ϵ > 0 \epsilon>0 ϵ>0,若存在 N > 0 N>0 N>0,当 n > N n>N n>N时,有 ∣ a n − A ∣ < ϵ |a_{n}-A|<\epsilon ∣an−A∣<ϵ,称 A A A为数列 { a n } \set{a_{n}} {an}的极限,记为 lim n → ∞ a n = A \lim\limits_{n\to{\infin}}{a_n}=A n→∞liman=A或记为 x n → a ( n → ∞ ) x_n\rightarrow a(n\rightarrow \infin) xn→a(n→∞),不引起混淆的情况下,还可以简写为 x n → a x_n\to{a} xn→a
- 半形式化语言描述: ∀ ε > 0 , ∃ N > 0 , \forall \varepsilon>0,\exist N>0, ∀ε>0,∃N>0, when: n > N n>N n>N,then: ∣ a n − A ∣ < ε |a_n-A|<\varepsilon ∣an−A∣<ε,记为 lim n → + ∞ a n = A \lim\limits_{n\to{+\infin}}a_{n}=A n→+∞liman=A
极限表达式成立的证明
- 证明数列极限的常用方法是用数列极限的定义证明
- 若 lim n → ∞ x n = a \lim\limits_{n\to\infin}{x_n}=a n→∞limxn=a,则 lim n → ∞ ∣ x n ∣ = ∣ a ∣ \lim\limits_{n\to\infin}{|x_n|}=|a| n→∞lim∣xn∣=∣a∣
- 由条件, ∀ ϵ > 0 \forall{\epsilon}>0 ∀ϵ>0, ∃ N > 0 \exist{N>0} ∃N>0,当 n > N n>N n>N时有 ξ = ∣ x n − a ∣ < ϵ \xi=|x_n-a|<\epsilon ξ=∣xn−a∣<ϵ
(1) - 构造 Δ = ∣ ∣ x n ∣ − ∣ a ∣ ∣ \Delta=||x_n|-|a|| Δ=∣∣xn∣−∣a∣∣,只要说明 ∀ ϵ > 0 \forall{\epsilon}>0 ∀ϵ>0, ∃ N > 0 \exist{N>0} ∃N>0,当 n > N n>N n>N时有 Δ < ϵ \Delta<\epsilon Δ<ϵ,即可证明结论成立
- 由绝对值不等式, Δ < ∣ x n − a ∣ \Delta<|x_n-a| Δ<∣xn−a∣
(2),(2)代入(1),得 Δ < ϵ \Delta<\epsilon Δ<ϵ,所以 lim n → ∞ ∣ x n ∣ = ∣ a ∣ \lim\limits_{n\to\infin}{|x_n|}=|a| n→∞lim∣xn∣=∣a∣ - Note:该命题的逆命题不成立,因为 Δ < ϵ \Delta<\epsilon Δ<ϵ ⇏ \not\Rightarrow ⇒ ξ < ϵ \xi<\epsilon ξ<ϵ;例如: x n = ( − 1 ) n x_n=(-1)^n xn=(−1)n,则 lim n → ∞ ∣ x n ∣ = 1 = ∣ 1 ∣ \lim\limits_{n\to\infin}{|x_n|}=1=|1| n→∞lim∣xn∣=1=∣1∣;而 lim n → ∞ ( − 1 ) n \lim\limits_{n\to\infin}{(-1)^{n}} n→∞lim(−1)n不存在
- 由条件, ∀ ϵ > 0 \forall{\epsilon}>0 ∀ϵ>0, ∃ N > 0 \exist{N>0} ∃N>0,当 n > N n>N n>N时有 ξ = ∣ x n − a ∣ < ϵ \xi=|x_n-a|<\epsilon ξ=∣xn−a∣<ϵ
- 推论:
- 若 lim n → ∞ x n = 0 \lim\limits_{n\to\infin}{x_n}=0 n→∞limxn=0,的充要条件是: lim n → ∞ ∣ x n ∣ = 0 \lim\limits_{n\to\infin}{|x_n|}=0 n→∞lim∣xn∣=0
- 有上结论可知必要性成立
- 充分性:若 lim n → ∞ ∣ x n ∣ = 0 \lim\limits_{n\to\infin}{|x_n|}=0 n→∞lim∣xn∣=0, ∀ ϵ > 0 \forall{\epsilon}>0 ∀ϵ>0, ∃ N > 0 \exist{N>0} ∃N>0,当 n > N n>N n>N时有 Δ = ∣ ∣ x n ∣ − 0 ∣ < ϵ \Delta=||x_n|-0|<\epsilon Δ=∣∣xn∣−0∣<ϵ成立,即 ∣ ∣ x n − 0 ∣ ∣ = ∣ x n − 0 ∣ < ϵ ||x_n-0||=|x_n-0|<\epsilon ∣∣xn−0∣∣=∣xn−0∣<ϵ,从而 lim n → ∞ x n = 0 \lim\limits_{n\to\infin}{x_n}=0 n→∞limxn=0
- 若 lim n → ∞ x n = 0 \lim\limits_{n\to\infin}{x_n}=0 n→∞limxn=0,的充要条件是: lim n → ∞ ∣ x n ∣ = 0 \lim\limits_{n\to\infin}{|x_n|}=0 n→∞lim∣xn∣=0
极限发散证明
- 证明极限发散,即证明数列极限不存在,仍然可以通过极限的定义入手证明
- 通常是通过取一个正数 ϵ = ϵ 0 > 0 \epsilon=\epsilon_0>0 ϵ=ϵ0>0说明 ϵ 0 \epsilon_0 ϵ0的取值下,“ ∄ N ∈ Z \not\exist{N}\in\mathbb{Z} ∃N∈Z,能使得当 n > N n>N n>N, ∣ x n − a ∣ < ϵ 0 |x_{n}-a|<\epsilon_0 ∣xn−a∣<ϵ0恒成立”
- 例:
- 证明数列 x n = ( − 1 ) n + 1 x_n=(-1)^{n+1} xn=(−1)n+1, ( n = 1 , 2 , ⋯ ) (n=1,2,\cdots) (n=1,2,⋯)是发散的
- 若数列收敛,则其有唯一极限,不妨设极限存在且等于 a a a,
- 按极限定义,对于 ∀ ϵ > 0 \forall{\epsilon}>0 ∀ϵ>0, ∃ N ∈ N + \exist{N}\in\mathbb{N_+} ∃N∈N+,当 n > N n>N n>N时有 ∣ x n − a ∣ < ϵ |x_n-a|<\epsilon ∣xn−a∣<ϵ
- 对于本例,不妨取 ϵ = 1 2 \epsilon=\frac{1}{2} ϵ=21,则 ∣ x n − a ∣ < 1 2 |x_n-a|<\frac{1}{2} ∣xn−a∣<21,而根据 x n x_n xn的同向公式可知, x n x_n xn重复取 − 1 , 1 -1,1 −1,1,当 x n = − 1 x_n=-1 xn=−1时, ∣ − 1 − a ∣ > 1 {|-1-a|}>1 ∣−1−a∣>1,与 ∣ x n − a ∣ < 1 2 |x_n-a|<\frac{1}{2} ∣xn−a∣<21矛盾,从而 { x n } \set{x_n} {xn}不存在极限 a a a
- 所以 { x n } \set{x_n} {xn}发散
常用数列极限
- lim n → ∞ q n \lim\limits_{n\to\infin}{q^{n}} n→∞limqn= 0 0 0, ∣ q ∣ < 1 |q|<1 ∣q∣<1;
- lim n → ∞ 1 n α = 0 \lim\limits_{n\to\infin}{\frac{1}{n^{\alpha}}}=0 n→∞limnα1=0, α > 0 \alpha>0 α>0
数列极限的几何意义
- lim n → ∞ x n = a \lim\limits_{n\to{\infin}}x_n=a n→∞limxn=a的几何意义是:以数轴为背景,对于 a a a点的任意 ϵ \epsilon ϵ邻域 U ( a , ϵ ) U(a,\epsilon) U(a,ϵ),即开区间 ( a − ϵ , a + ϵ ) (a-\epsilon,a+\epsilon) (a−ϵ,a+ϵ),一定存在 N N N,使得当 n > N n>N n>N,即第 N N N项后的点 x n x_n xn都落在开区间 U ( a , ϵ ) U(a,\epsilon) U(a,ϵ)内,而只有有限个点落在该区间以外
例
- lim n → ∞ ( n + 1 n ) ( − 1 ) n \lim\limits_{n\to\infin}(\frac{n+1}{n})^{(-1)^{n}} n→∞lim(nn+1)(−1)n= 1 1 1
- 分析: lim n → ∞ ( 2 n 2 n − 1 ) \lim\limits_{n\to\infin}(\frac{2n}{2n-1}) n→∞lim(2n−12n)=1; lim n → ∞ ( 2 n + 1 2 n ) \lim\limits_{n\to\infin}(\frac{2n+1}{2n}) n→∞lim(2n2n+1)=1
函数的极限
- 另见: 函数极限
相关文章:

AM@数列极限
文章目录 abstract极限👺极限的主要问题 数列极限数列极限的定义 ( ϵ − N ) (\epsilon-N) (ϵ−N)语言描述极限表达式成立的证明极限发散证明常用数列极限数列极限的几何意义例 函数的极限 abstract 数列极限 极限👺 极限分为数列的极限和函数的极限…...
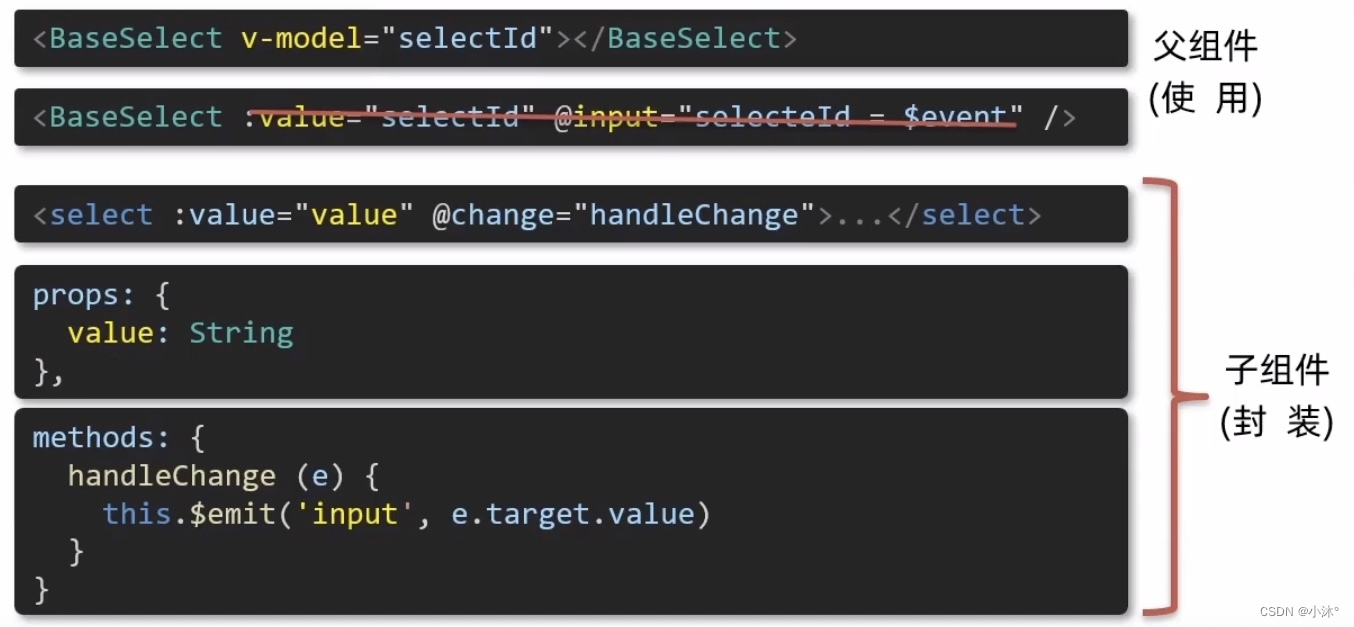
Vue-2.3v-model原理
原理:v-model本质上是一个语法糖,例如应用在输入框上,就是value属性和input事件的合写。 作用:提供数据的双向绑定 1)数据变,视图跟着变:value 2)视图变,数据跟着变input 注意&a…...

左手 Serverless,右手 AI,7 年躬身的古籍修复之路
作者:宋杰 “AI 可以把我们思维体系当中,过度专业化、过度细分的这些所谓的知识都替代掉,让我们集中精力去体验自己的生命。我挺幸运的,代码能够有 AI 辅助,也能够有 Serverless 解决我的运营成本问题。Serverless 它…...

计算mask的体素数量
import numpy as np import nibabel as nib # 用于处理神经影像数据的库 # 从文件中加载mask图像 mask_image nib.load(rE:\mask.nii.gz) # 获取图像数据 mask_data mask_image.get_fdata() # 计算非零像素的数量,即白质骨架的体素总数 voxel_count np.count_no…...

VR全景营销颠覆传统营销,让消费者身临其境
随着VR的普及,各种VR产品、功能开始层出不穷,并且在多个领域都有落地应用,例如文旅、景区、酒店、餐饮、工厂、地产、汽车等,在这个“内容为王”的时代,VR全景展示也是一种新的内容表达方式。 VR全景营销让消费者沉浸式…...
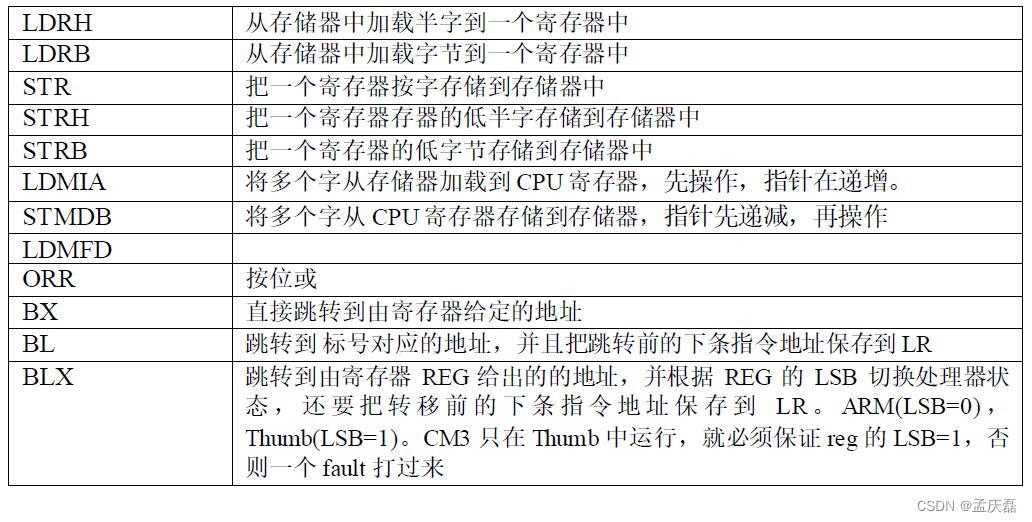
FreeRTOS学习笔记——四、任务的定义与任务切换的实现
FreeRTOS学习笔记——四、任务的定义与任务切换的实现 0 前言1 什么是任务2 创建任务2.1 定义任务栈2.2 定义任务函数2.3 定义任务控制块2.4 实现任务创建函数2.4.1 任务创建函数 —— xTaskCreateStatic()函数2.4.2 创建新任务——prvInitialiseNewTask()函数2.4.3 初始化任务…...
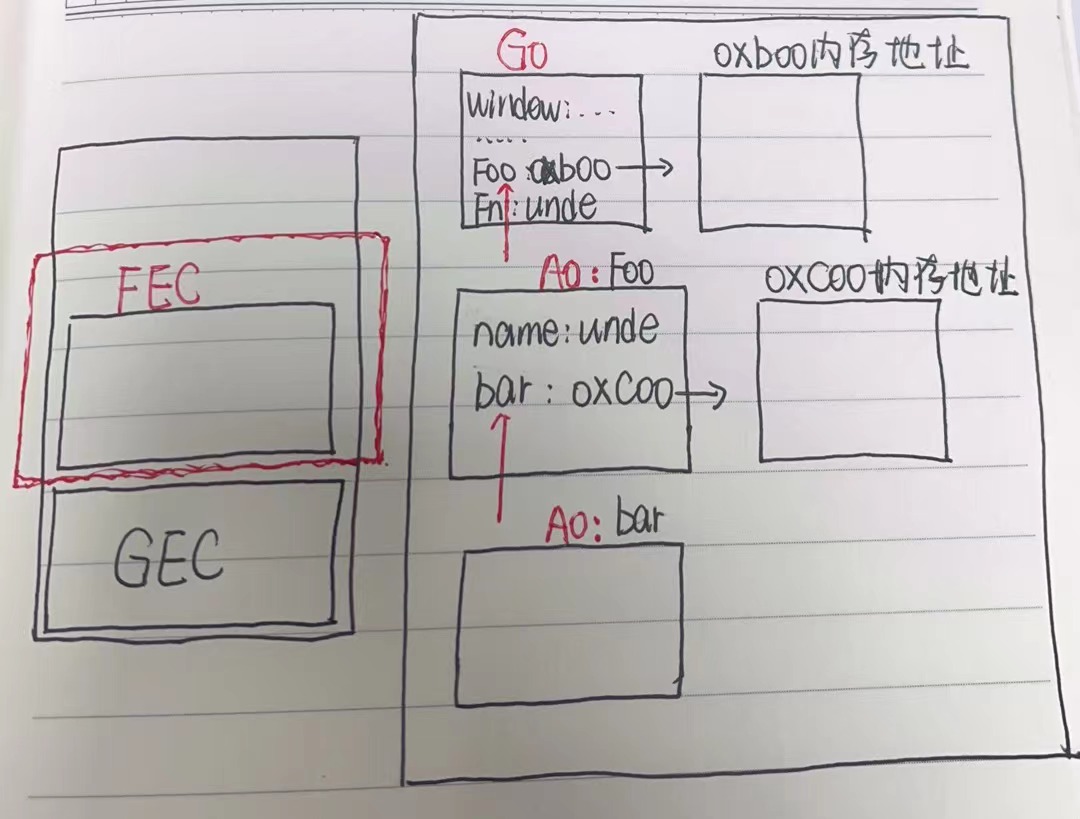
js 之让人迷惑的闭包 03
文章目录 一、闭包是什么? 🤦♂️二、闭包 😎三、使用场景 😁四、使用场景(2) 😁五、闭包的原理六、思考总结一、 更深层次了解闭包,分析以下代码执行过程二、闭包三、闭包定义四、…...

10月10日上课内容 Docker--harbor私有仓库部署与管理
Docker--harbor私有仓库部署与管理 ------------------ 1、搭建本地私有仓库 ------------------------------ #首先下载 registry 镜像 docker pull registry #在 daemon.json 文件中添加私有镜像仓库地址 vim /etc/docker/daemon.json { "insecure-registries"…...

Java 序列化和反序列化为什么要实现 Serializable 接口
第一、序列化和反序列化 序列化:把对象转换为字节序列的过程称为对象的序列化. 反序列化:把字节序列恢复为对象的过程称为对象的反序列化. 第二、什么时候需要用序列化和反序列化呢? 当我们只在本地JVM里运行下Java实例, 这个时候是不需要什么序列化和…...
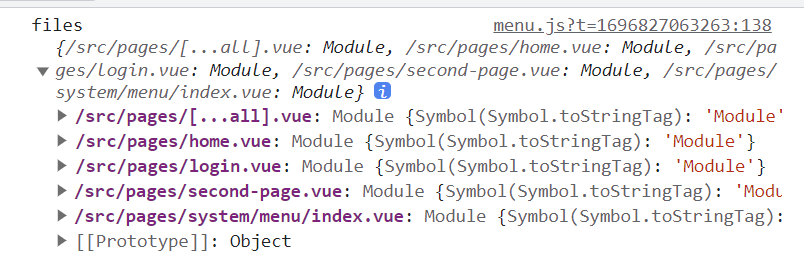
vite+vue3+ts中使用require.context | 报错require is not defined | 获取文件夹中的文件名
vitevue3ts中使用require.context|报错require is not defined|获取文件夹中的文件名 目录 vitevue3ts中使用require.context|报错require is not defined|获取文件夹中的文件名一、问题背景二、报错原因三、解决方法 一、问题背景 如题在vitevue3ts中使用required.context时报…...

C#(Csharp)我的基础教程(四)(我的菜鸟教程笔记)-Windows项目结构分析、UI设计和综合事件应用的探究与学习
目录 windows项目是我们.NET学习一开始必备的内容。 1、窗体类(主代码文件窗体设计器后台代码文件) 主窗体对象的创建:在Program类里面: Application.Run(new FrmMain());这句代码就决定了,当前窗体是项目的主窗体。…...

Flink: Only supported for operators
Exception in thread "main" java.lang.UnsupportedOperationException: Only supported for operators.at org.apache.flink.streaming.api.scala.DataStream.name(...
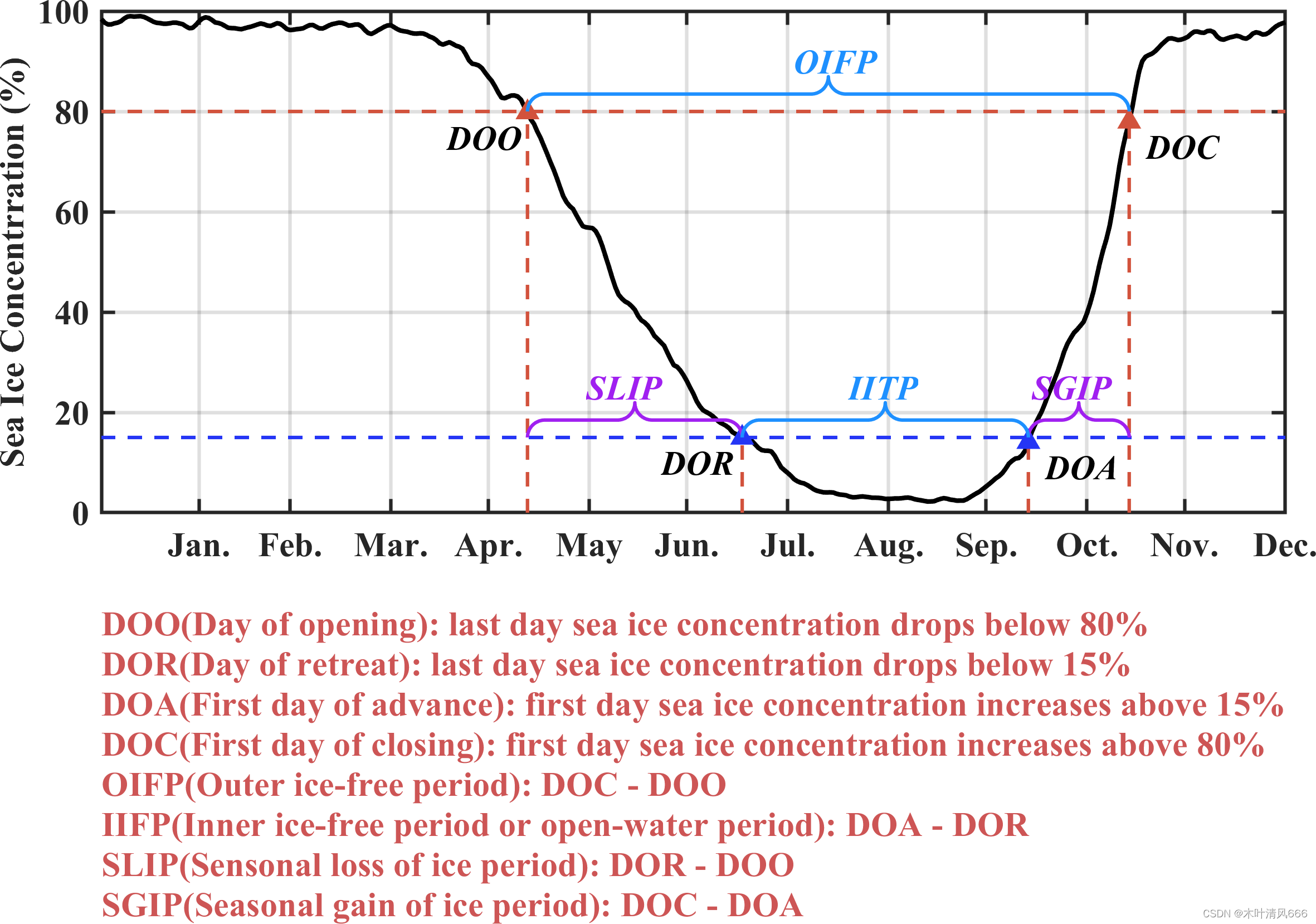
NSIDC定义的海冰相关概念
文章目录 相关概念Matlab绘图结果展示 相关概念 NSIDC 表示 “National Snow and Ice Data Center”,即美国国家雪和冰数据中心。NSIDC 是一个位于美国科罗拉多大学波尔得分校的研究中心,致力于收集、管理和分发全球雪和冰的科学数据。 Matlab绘图 cl…...

【码银送书第八期】《Python数据挖掘:入门进阶与实用案例分析》
摘要:本案例将主要结合自动售货机的实际情况,对销售的历史数据进行处理,利用pyecharts库、Matplotlib库进行可视化分析,并对未来4周商品的销售额进行预测,从而为企业制定相应的自动售货机市场需求分析及销售建议提供参…...
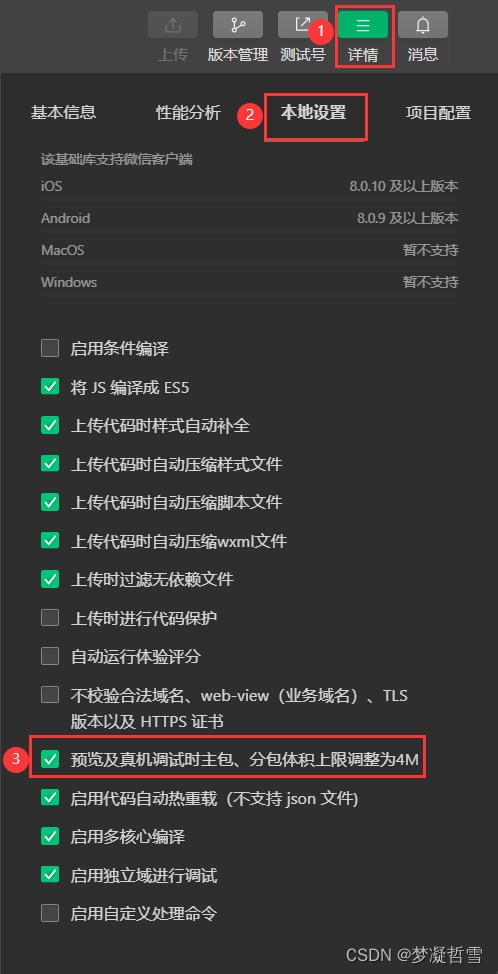
微信小程序底部tabBar不显示图标
现场还原 在设置微信小程序底部tabBar导航图标时,无论如何操作均无法显示在界面上 解决思路 问题1 图标类型 一开始以为不支持png类型,但查看官方API仅提示ICON尺寸大小 打开其他项目可以正常展示,排除图标类型问题 iconPath string 否 …...

PostgreSQL基操之角色、表空间、数据库与表
PostgreSQL基操之角色、表空间、数据库与表 角色创建与管理表空间创建与管理数据库创建与管理表创建与管理 角色创建与管理 PostgreSQL数据库里没有User的概念,只有Role的概念。有的Role可以用于登录数据库,这些Role与其他数据库中的用户等价。 --创建…...

【算法|滑动窗口No.1】leetcode209. 长度最小的子数组
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...

11_博客管理系统_实现过程
项目初始化 创建项目文件夹进入文件夹,执行 npm init -y 命令安装 express 和 mongoose,npm install express mongoose创建项目入口文件,app.js 或 index.js在 app.js 中进行项目搭建配置网站的路由配置网站静态资源目录 配置静态页面 配置…...
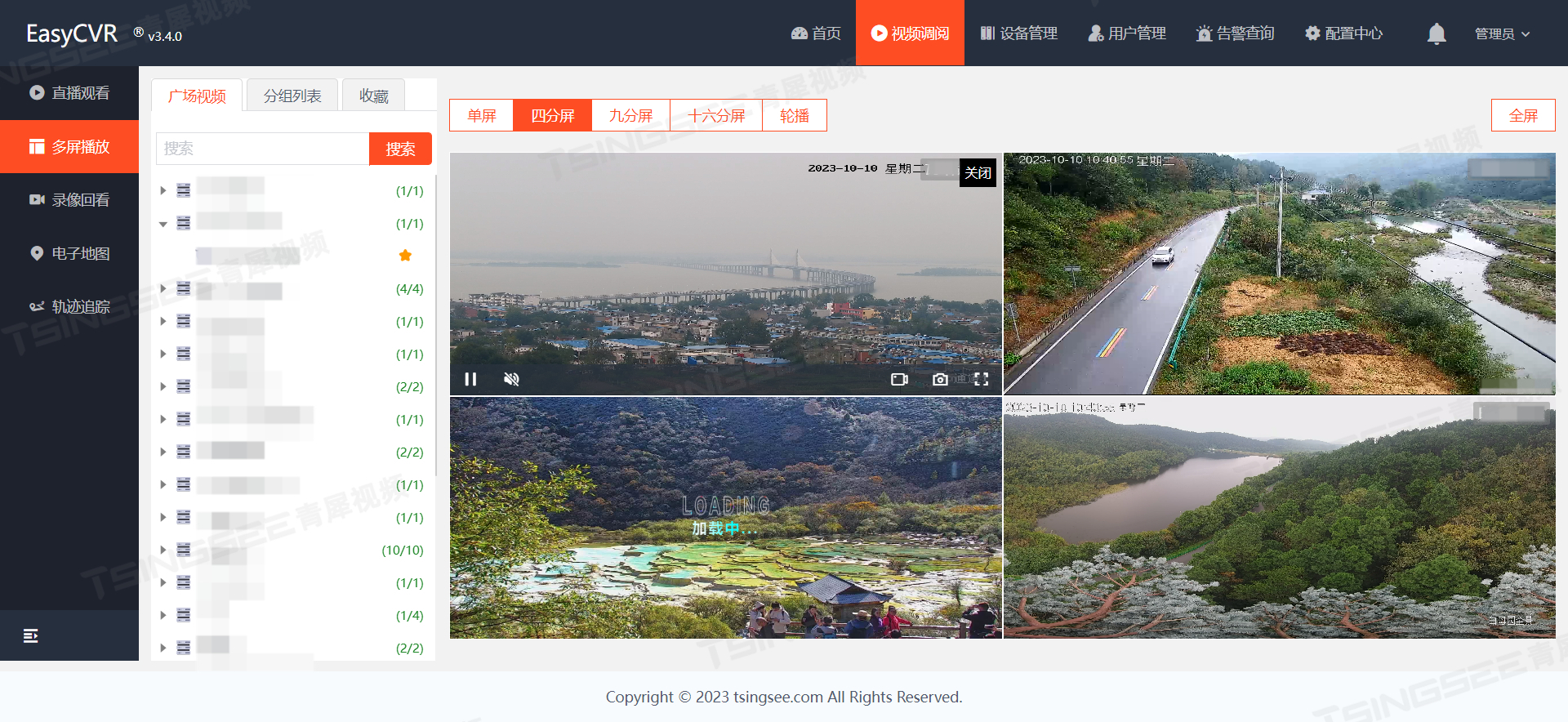
安防视频监控平台EasyCVR集成到ios系统不能播放是什么原因?如何解决?
视频监控TSINGSEE青犀视频平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,在视频监控播放上,TSINGSEE青犀视频安防监控汇聚平台可支持1、4、9、16个画面窗口播放,可同时播放多路视频流&#…...

hutool实现文件上传与下载
<dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.8.16</version></dependency> 文件上传需要创建一个表 Autowiredprivate SysFileInfoMapper sysFileInfoMapper;Value("${ty.…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...
