CART 算法——决策树
目录
1.CART的生成:
(1)回归树的生成
(2)分类树的生成
①基尼指数
②算法步骤
2.CART剪枝:
(1)损失函数
(2)算法步骤:
CART是英文“classification and regression tree”的缩写,翻译过来是分类与回归树,与前面说到的ID3、C4.5一致,都是决策树生成的一种算法,同样也由特征选择、树的生成以及剪枝组成,既可以用于分类也可以用于回归。CART算法由决策树的生成以及决策树剪枝两部分组成。
1.CART的生成:
决策树的生成就是递归地构建二叉决策树的过程。对回归树用平方差最小化准则,对分类树用基尼指数最小化准则,进行特征选择,生成二叉树。
分类树与回归树的一个区别是:如果目标变量是离散型变量则用分类树,如果目标变量是连续型变量则用回归树。
(1)回归树的生成
回归树是用于目标变量是连续型变量的情况下,假设X与Y分别为输入和输出变量,并且Y是连续型变量,给定数据即D={(x1,y1),(x2,y2),...(xn,yn)},根据训练数据集D生成决策树。
前面说过,回归树的生成准则是平方差(总离差平方和:实际观察值与一般水平即均值的离差总和)最小化准则,即预测误差最小化,所以我们的目的就是找到一个分界点,以这个点作为分界线将训练集D分成两部分D1和D2,并且使数据集D1和D2中各自的平方差最小。然后然后再分别再D1和D2中找类似的分界点,继续循环,直到满足终止条件。
在具体找分解值的时候采用遍历所有变量的方法,依次计算平方差,选择平方差最小时对应的分解值。
(2)分类树的生成
分类树用基尼指数选择最优特征(与信息增益类似),同时决定该特征的最优二值切分点。
①基尼指数
基尼指数Gini(D)表示集合D的不确定性,基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。基尼指数数值越大,样本集合的不确定性越大。
分类问题中,假设有K个类,样本点属于第k类的概率为pk,则概率分布的基尼指数定义为:

对于二分类问题,若样本点属于第一类的概率为p,则概率分布的基尼指数为:Gini(p)=2p(1-p)。
对于样本给定的集合D,其基尼指数为:Gini(D)=1-∑(|Ck|/|D|)*2,这里Ck是D中属于第k类的样本子集,K是类的个数。
条件基尼指数:

上面公式表示在特征A的条件下,集合D的基尼指数,其中D1和D2表示样本集合D根据特征A是否取某一个可能值a被分割成的两部分。
②算法步骤
输入:训练数据集D,停止计算的条件
输出:CART决策树
根据训练数据集,从根节点开始,递归地对每个结点进行以下操作,构建二叉决策树:
设结点的训练数据集为D,计算现有特征对该数据集的基尼指数,此时,对每一个特征A,对其可能取的每一个值a,根据样本点A=a的测试为“是”或“否”将D分割成D1和D2两部分,然后计算Gini(D,A)。
在所有可能的特征A以及他们所有可能的切分点a中,选择基尼指数最小的特征及其对应的切分点作为最优特征与最佳切分点。依最优特征与最优切分点,从现结点生成两个子节点,将训练数据集依特征分配到两个子节点中去。
对两个子节点递归调用.1,.2,直至满足停止条件。
生成CART决策树。
算法停止计算的条件是结点中的样本个数小于预定的阈值,或样本集的基尼指数小于预定的阈值(样本基本属于同一类),或者没有更多特征。
2.CART剪枝:
我们再前面那一章节提过剪枝是为了避免数据发生过拟合现象,而避免这种情况发生的方法就是使损失函数最小化。
(1)损失函数
先看看损失函数的公式:

在α已知得情况下,要使上面得Cα(T)最小,就需要使|T|最小,即子树得叶节点数量最小;或者使训练误差最小,要使训练误差最小,就需要再引入新的特征,这样更会增加树得复杂度。所以我们主要通过降低|T|来降低损失函数,而这主要是通过剪去一些不必要得枝得到得。
但是在具体剪得过程中,我们需要有一个评判标准用来判断哪些枝可以剪,哪些使不可以剪得。而这个评判标准就是剪枝前后该树得损失函数是否减少,如果减小,就对该枝进行剪枝。
具体地,从整数T0开始剪枝,对T0的任意内部节点t,以t为单结点树(即该树没有叶节点)的损失函数是:Cα(t)=C(t)+α
以t为根节点的子树Tt的损失函数是:Cα(Tt)=C(Tt)+α|Tt|
当α=0或者充分小,有不等式:
![]()
当α继续增大时,在某一α处会有:

当α再继续增大时,在某一α处会有:
![]()
当下式成立时:
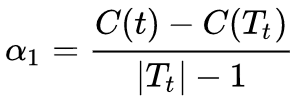
在这个时候,Tt与t有相同的损失函数值,而t的结点少,因此t比Tt更可取,对Tt进行剪枝。
为此,可以对T0中的每一内部节点t,计算g(t)=(C(t)-C(Tt))/(|Tt|-1),该式表示剪枝后整体损失函数减少的程度。在T0中剪去g(t)最小的Tt,将得到的子树作为T1,同时将最小的g(t)设为α1.T1为区间最小[α1,α2)的最优子数。如此剪枝下去,直至得到根节点,在这一过程中不断增加α的值,产生新的区间。
在剪枝得到的子树序列T0,T1,...,Tn中独立验证数据集,测试子树序列的T0,T1,...,Tn中各颗子树的平方误差或基尼指数。平方误差或基尼指数最小的决策树被认为是最优的决策树。
(2)算法步骤:
输入:CART算法生成的决策树T0
输出:最优决策树Tα
设k=0,T=T0
设α=+∞
自上而下地对各内部节点t计算C(Tt),|Tt|以及g(t),这里,Tt表示以t为根节点的子树,C(Tt)是对训练数据的预测误差。|Tt|是Tt的叶结点个数。
对g(t)=α的内部结点t进行剪枝,并对叶节点t以多数表决法决定其类得到树T。
设k=k+1,αk=α,Tk=T。
如果Tk不是由根节点及两个叶节点构成的树,则回到步骤(3);否则令Tk=Tn。
采用交叉验证法在子树序列T0,T1,...,Tn中选取最优子树Tα。
相关文章:
CART 算法——决策树
目录 1.CART的生成: (1)回归树的生成 (2)分类树的生成 ①基尼指数 ②算法步骤 2.CART剪枝: (1)损失函数 (2)算法步骤: CART是英文“class…...

CF1877A Goals of Victory
题目是说,有n个队伍进行足球赛,两两之间进行一场足球赛,会有一个积分,a:b,题目所说的efficiency表示的是一个队伍的得分减去对手队伍的得分 #include<bits/stdc.h> using namespace std;int num[110];int main(…...

018-第三代软件开发-整体介绍
第三代软件开发-整体介绍 文章目录 第三代软件开发-整体介绍项目介绍整体介绍Qt 属性系统QML 最新软件技术框架 关键字: Qt、 Qml、 属性、 Qml 软件架构 项目介绍 欢迎来到我们的 QML & C 项目!这个项目结合了 QML(Qt Meta-Object …...

储存数据文本json的读写
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言一、json文本介绍二、json文本的应用三、json文本的操作1、环境配置2、写入文件3、读取文件4、文件格式解析注意的点参考链接前言 认知有限,望大家…...

Java之动态代理的详细解析
2. 动态代理 2.1 好处: 无侵入式的给方法增强功能 2.2 动态代理三要素: 1,真正干活的对象 2,代理对象 3,利用代理调用方法 切记一点:代理可以增强或者拦截的方法都在接口中,接口需要写在…...
github Release 下载加速,绿色合法,遥遥领先
你有没有这样一个困惑,当你寻找了很久终于找到一个解决问题的方案,发现这个工具在 GitHub 上,接下来等待我们的就是遥遥无期的龟速下载。 文章目录 前言下载测试加速下载操作 视频讲解 遥遥领先 前言 GitHub 作为程序员的知识宝库ÿ…...

RabbitMQ消息中间件概述
1.什么是RabbitMQ RabbitMQ是一个由erlang开发的AMQP(Advanced Message Queue )的开源实现。AMQP 的出现其实也是应了广大人民群众的需求,虽然在同步消息通讯的世界里有很多公开标准(如 COBAR的 IIOP ,或者是 SOAP 等&…...
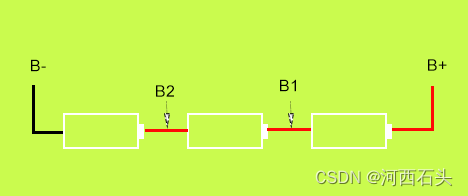
12V手电钻保护板如何接线演示
爱做手工的小伙伴们肯定会用到手电钻,那么电池消耗完了,或要换的,或要自己动手做几个备用电源,关键点就是电路保护板的接线。废话不多说,直接上板子看实操。 文章目录 一、线路板图1、输入接线2、输出接线 二、接线方法…...
基于SpringBoot的教学辅助平台
目录 前言 一、技术栈 二、系统功能介绍 学生信息管理 教师信息管理 课程信息管理 科目分类管理 班级分类管理 课程作业管理 交流论坛管理 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 随着信息技术在管理上越来越深入而广泛的应用,管理…...
)
Qt 读写数据流文件(转 CppGuiProgrammingWithQt4)
读取文件: update 20140525:添加线程处理,在读取大文件时优化,防止 app 出现 application 假死状态。 bool SpreadSheet::readFile(const QString &filePath){QFile file(filePath);if ( !file.open(QIODevice::ReadOnly)) …...

Pygame中将鼠标形状设置为图片2-2
3 编写主程序 在主程序中,首先创建屏幕并且完成一些准备工作,之后在while循环中不断更新sprite实例即可。 3.1 创建屏幕及准备工作 创建屏幕及准备工作的代码如图5所示。 图5 创建屏幕及准备工作 其中,第20行代码调用pygame.mouse模块中的…...
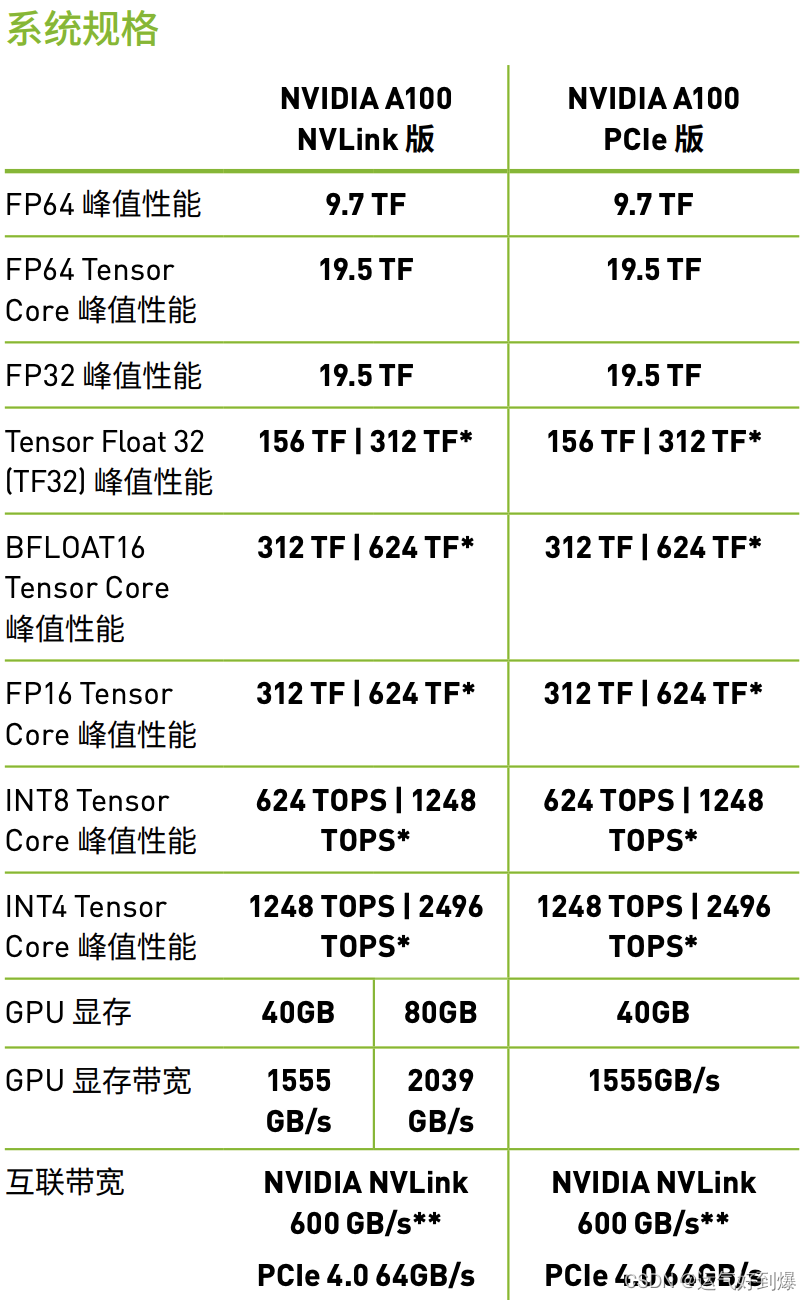
GPU 基础知识整理
萌新: 在接触一款硬件时我会:基础硬件结构,线程结构,内存布局,数据吞吐量,等方面进行学习 首先GPU的特点: 并行性能:GPU 是专门设计用于并行计算的硬件,通常具有大量的处理单元&am…...
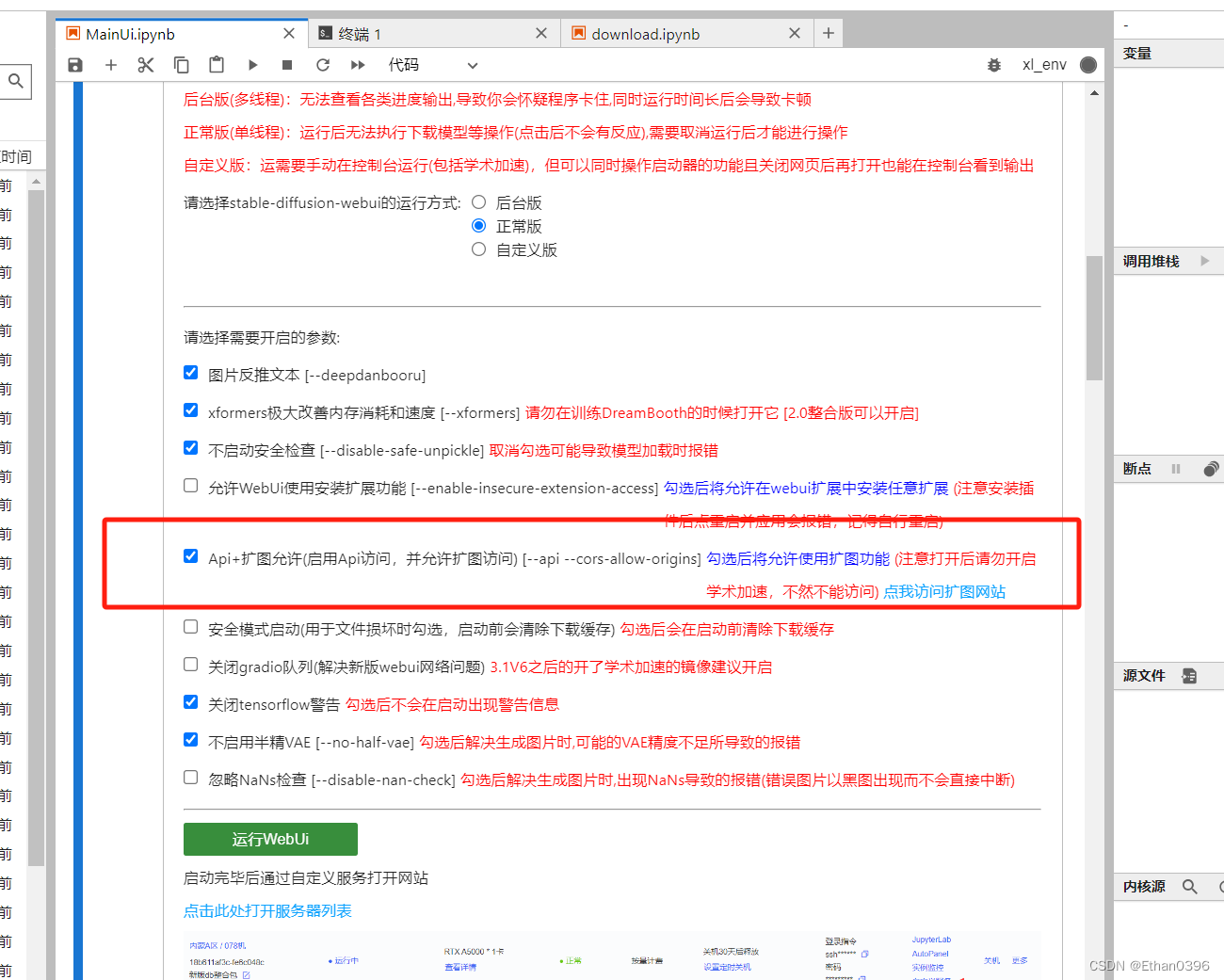
stable diffusion API接口 + 扩展接口
文章目录 概要流程页面接口调用展示txt2img接口AutoDL设置扩展接口 概要 调研Stable Diffusion二次开发,查看接口文档。 基于AutoDL算力服务器,直接安装部署,非常容易上手,部署教程放下面了。 部署教程 流程 页面接口调用 页面…...

MySQL数据库基本操作和完整性约束类型详解
目录 一、增删改查的sql语句二、表完整性约束1、表完整性约束的介绍2、常见的完整性约束类型3、表完整性约束实战操作3.1.主键primary key3.2.自增键auto_increment3.3.唯一键UNIQUE3.4.null与not null3.5.默认约束 一、增删改查的sql语句 SQL(Structured Query Lan…...

unity2022版本 实现加减进度条
简介 在现代游戏开发中,用户界面 (UI) 扮演着至关重要的角色,它不仅为玩家提供信息,还增强了游戏的可玩性。加减进度条是一种常见的UI元素,它可以用于显示游戏中的进度、倒计时、资源管理和其他关键信息。在这篇博客中࿰…...

COCO数据集中图像的caption读取到txt文件
annotations_trainval2017.zip import os import shutil import jsoncaptions_path r"G:\SketchDiffusion\Sketchycoco\Dataset\annotations\captions_train2017.json" # 读取json文件 with open(captions_path, r) as f1:dictortary json.load(f1)# 得到images和…...

再谈Java泛型
一.类型参数的约束 我们可以对泛型传进来的参数做一些约束,比如说 用extends表明传进来的参数类型必须是必须是某个类型的子类型或者本身 当然也可以用接口约束,也是用extends表明传进来的参数类型必须实现某个接口。用&连接,注意class…...

scss使用自定义函数实现单位像素随屏幕比例动态缩放
vue中通过变量和scss函数来动态实现动态缩放像素 简单来说就是比例缩小时,像素单位变大,从而字体大小相对不变,以下仅处理比例缩小的状况 自定义一个属性–size,初始值为1px template <template><div class"hom…...

Django 静态自定义化配置
STATIC # APP本地静态资源目录(就APP对应的) STATIC_URL "/static/"# 远程静态文件URL(少用) REMOTE_STATIC_URL# 外部引用静态文件目录(外层的) STATICFILES_DIRS [os.path.join(BASE_DIR, &…...
TensorFlow入门(十四、数据读取机制(1))
TensorFlow的数据读取方式 TensorFlow的数据读取方式共有三种,分别是: ①预加载数据(Preloaded data) 预加载数据的方式,其实就是静态图(Graph)的模式。即将数据直接内嵌到Graph中,再把Graph传入Session中运行。 示例代码如下: import tensorflow.compat.v1 as tf tf.disabl…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
