第五章 图
第五章 图
- 图的基本概念
- 图的应用背景
- 图的定义和术语
- 图的存储结构
- 邻接矩阵
- 邻接表
- 图的遍历
- 连通图的深度优先搜索
- 连通图的广度优先搜索
- 图的应用
- 最小生成树
- 拓扑排序
- 小试牛刀
图的基本概念
图结构中,任意两个结点之间都可能相关;而在树中,结点具有层次关系,每一层结点只能和上一层至多一个结点相关,但可能和下一层多个结点相关
图的应用背景
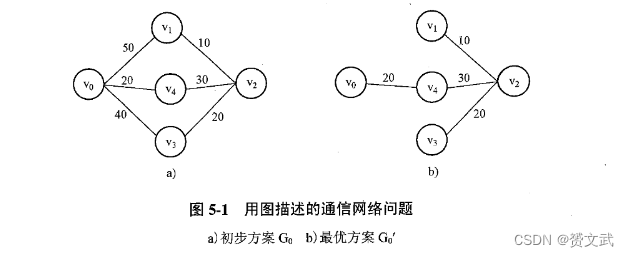
- 上图中圆圈称为顶点;连线称为边,连线附带的数值称为边的权
- 图结构可以用来描述通信网络
图的定义和术语
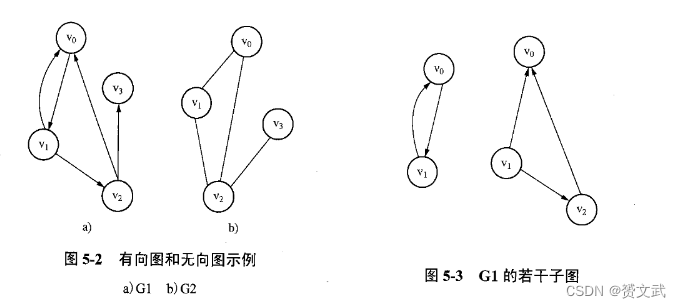
图G由两个集合V和E组成,记作G=(V,E);V是顶点的集合(有穷非空),E是边的集合
- 有向图:边是有序的(边带箭头“单行道”、用<顶点1,顶点2>表示从顶点1到顶点2的边);无向图:边是无序的(边不带箭头、用(顶点1,顶点2)表示顶点1和2之间的边)
- 弧,弧头,弧尾;弧:有向图的边称为弧;<v,w>表示从v到w的一条弧,其中v称为弧尾(或始点),w称为弧头(或终点)
任何两点之间都有边的无向图称为无向完全图;任何两点之间都有弧的有向图称为有向完全图
- 权:图的边的附带数值,实际应用中可以表示从一个顶点到另一个顶点的距离、代价或耗费等
- 带权图:每条边都带权的图称为带权图
- 顶点的度D、入度ID、出度OD:无向图中顶点的度是与该顶点相关联的边的数目,有向图中则把以顶点为终点的弧的数目称为该顶点的入度,以该顶点为始点的弧的数目称为该顶点的初读,有向图中的度为入度和出度的和
- 子图:设G=(V,E)是一个图,若E’是E的子集,V’是V的子集,并且E’中的边仅有与V’中的顶点相关联。则G’称为G的子图
- 路径、路径长度:从一个顶点到另一个顶点称为路径;路径长度就是路径(或弧)上边的数之和
- 简单路径、回路、简单回路;简单路径:序列中顶点不重复出现;第一个顶点和最后一个顶点相同的路径称为回路或环;除了第一个顶点和最后一个顶点外,其余顶点不重复的回路称为简单回路或简单环
- 连通、连通图、联通分量;连通图:在无向图中,如果从顶点v到顶点v’有路径,则称其为连通;连通图:图中任意两个顶点都是连通的;连通分量:无向图中的极大连通子图
- 强连通、强连通图、强连通分量;强连通图:有向图任意一对顶点双向连通;强连通分量:有向图的极大连通子图
- 生成树、生成森林;生成树:包含所有顶点的一个极小连通子图;生成森林:在非连通图中,每个连通分量都可得到一个极小的连通子图,即一棵生成树,这些连通分量的生成树就组成了一个非连通图的生成森林
图的存储结构
邻接矩阵
- 二维矩阵来实现,两顶点连通为1,不连通为0,行,列分别表示全部顶点,如下图所示:

注:也可用邻接矩阵表示带权图,没有边的用无穷表示,有的则用权,其余正常
邻接表
邻接表是顺序存储与链式存储相结合的存储方式

-
有向图的邻接表;以顶点Vi为尾的弧
-
无向图的邻接表;第i个单链表中的结点表示依赖于Vi的边
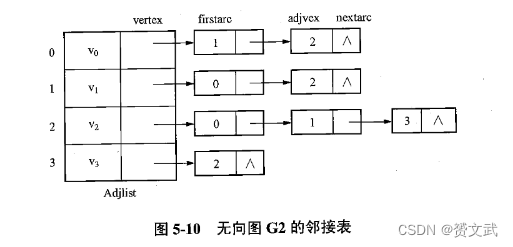
- 逆邻接表:逆邻接表是指以每个顶点作为索引,记录各个顶点的入边(即指向该顶点的边)的数据结构。(有向图的邻接表记录的是出边)
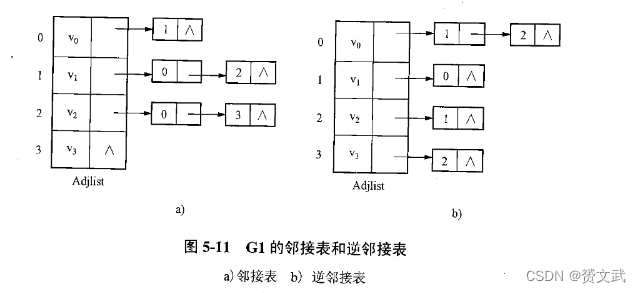
图的遍历
图的遍历是指从图的某个顶点出发,系统的访问图的每个顶点,并且每个顶点只能被访问一次
连通图的深度优先搜索
以图中某个顶点出发,首先访问出发点,然后任选一个未访问过的邻接点,以邻接点为新出发点继续,依此类推,直到所有顶点都被访问
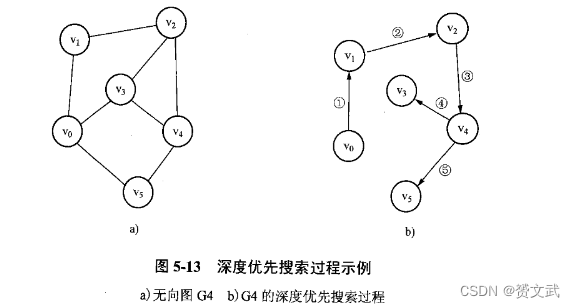
连通图的广度优先搜索
从图中某个顶点出发,访问了该顶点后依次访问该顶点的邻接点,然后从邻接点出发继续访问直到结束
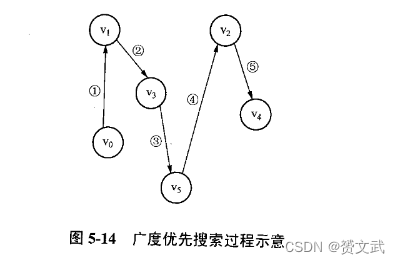
图的应用
最小生成树
对于有n个顶点的无向图,所有生成树都有且仅有n-1条边
- Prim算法(假设G=(V,E)是一个带权图,生成的最小生成树为MinT=(V,T),其中V为顶点的集合,T为边的集合)
- 初始化:U={u0},T={}。其中U为一个新设置的顶点的集合,初始U中只含有顶点u0,这里假设从顶点u0出发
- 对所有u∈U,v∈V-U中,找一条权最小的边(u’,v’),将这条边加入集合T中,将顶点v’加入集合U中
- 如果U=V,则算法结束,否则重复
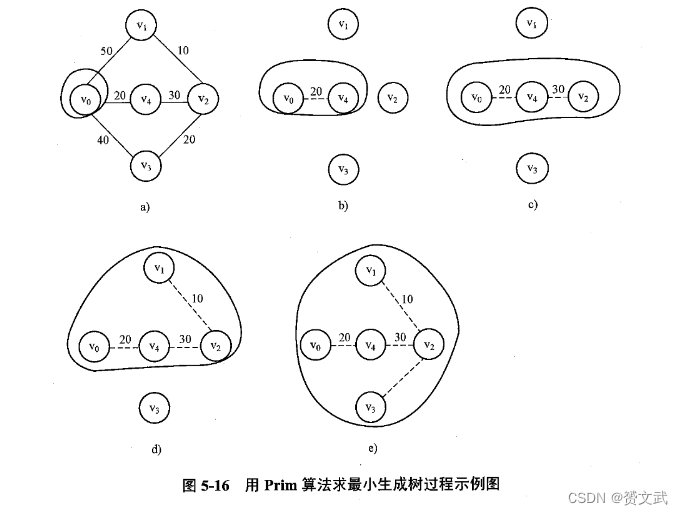
- 克鲁斯卡尔算法
- 设G=(V,E),令最小生成树初始状态为只有n个顶点而无边的非连通图T=(V,{}),每个顶点自成一个连通分量
- 在E中选取代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边,选取下一条代价最小的边
- 依此类推,直到T中所有顶点都在同一连通分量上为止
- Dijkstra求单源最短路径(设置顶点集合S,开始时S中只含有源点v)
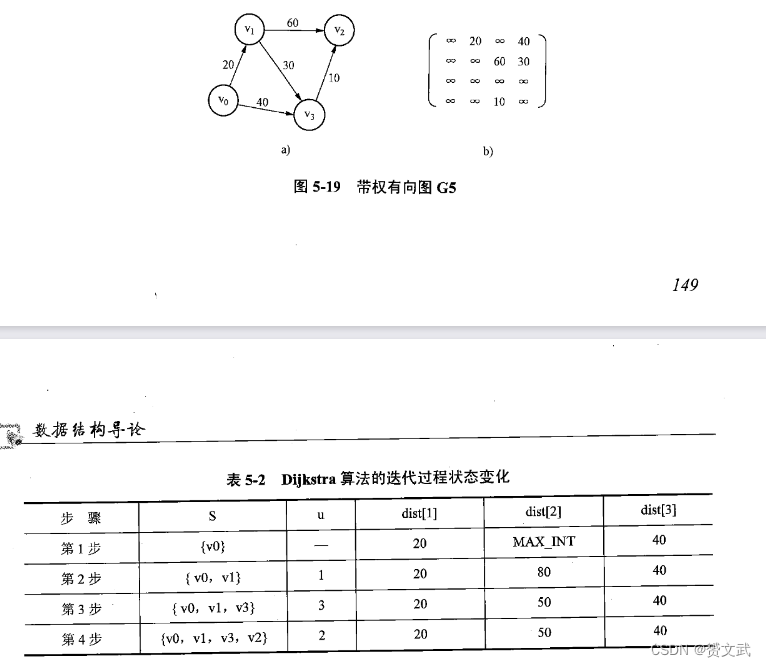
- 创建一个节点集合,初始时只包含起点节点,以及一个距离表记录起点到各个节点的当前最短距离和路径。
- 从起点开始,遍历与起点相邻的节点,并更新距离表中的距离和路径。
- 选择一个距离表中未访问过的节点中距离最短的节点,将其加入节点集合中,并继续遍历与该节点相邻的节点。若找到更短的路径,更新距离表中的距离和路径。
- 重复步骤3,直到所有节点都被加入节点集合,或者目标节点被加入节点集合。最终,距离表中记录的就是起点到各个节点的最短距离和路径。
拓扑排序
- AOV网:工程或者某种流程可分为若干个小的工程或阶段,这些小的工程或阶段就称为活动;若以图中顶点表示活动,有向边表示活动之间的优先关系,这种有向图称为AOV网
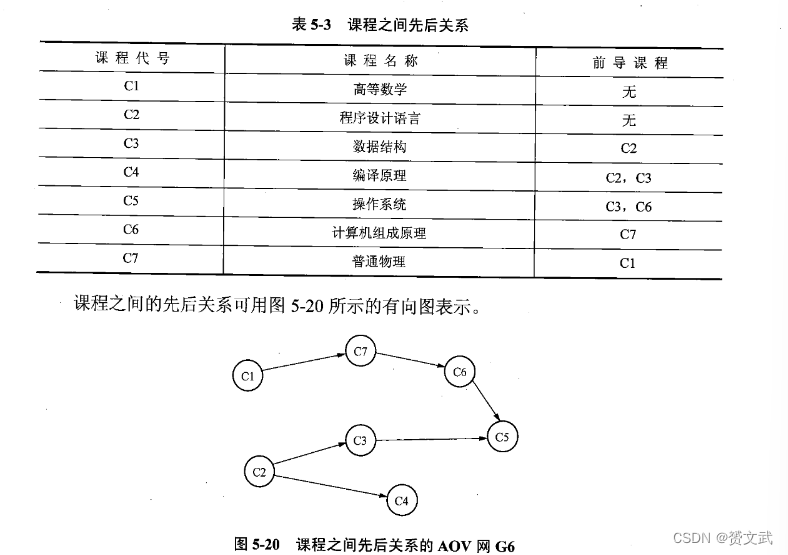
- 拓扑排序
完成拓扑排序的前提条件是AOV网中不能出现回路
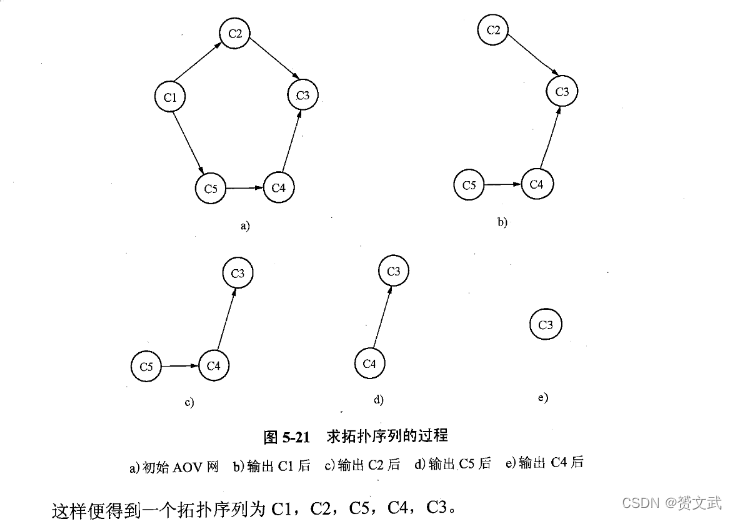
有向图拓扑排序算法的基本步骤如下:
- 图中选择一个入度为0的顶点,输出该顶点
- 从图中删除该顶点及其相关联的弧,调整被删弧的弧头结点的入度(入度减1)
- 重复执行上述步骤直到所有入度为0的顶点均被输出
小试牛刀
- 一个有n个顶点的无向连通图,最少有______条边
- 无向图的邻接矩阵是_______矩阵
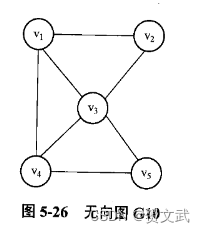
- 给出下图的邻接矩阵和邻接表
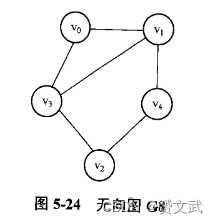
- 分别给出下图的邻接矩阵、邻接表和逆邻接表
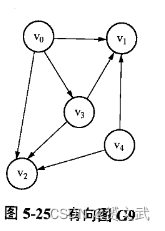
- 分别给出下图从v5出发按深度优先搜索和广度优先搜索算法遍历得到的顶点序列
相关文章:

第五章 图
第五章 图 图的基本概念图的应用背景图的定义和术语 图的存储结构邻接矩阵邻接表 图的遍历连通图的深度优先搜索连通图的广度优先搜索 图的应用最小生成树拓扑排序 小试牛刀 图的基本概念 图结构中,任意两个结点之间都可能相关;而在树中,结点…...

深度学习实战:用Keras搭建深度学习网络做手写数字识别
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。 🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、…...

算法解析:LeetCode——机器人碰撞和最低票价
摘要:本文由葡萄城技术团队原创并首发。转载请注明出处:葡萄城官网,葡萄城为开发者提供专业的开发工具、解决方案和服务,赋能开发者。 机器人碰撞 问题: 现有 n 个机器人,编号从 1 开始,每个…...
LeetCode刷题总结 - LeetCode 热题 100 - 持续更新
LeetCode 热题 100 其他系列哈希1. 两数之和49. 字母异位词分组128. 最长连续序列 双指针27. 移除元素283. 移动零11. 盛最多水的容器剑指 Offer II 007. 数组中和为 0 的三个数42. 接雨水 滑动窗口438. 找到字符串中所有字母异位词3. 无重复字符的最长子串 字串560. 和为 K 的…...
Spring是什么?为什么要使用Spring?
目录 前言 一、Spring是什么? 1.1 轻量级 1.2 JavaEE的解决方案 二、为什么要使用Spring 2.1 传统方式完成业务逻辑 2.2 使用Spring模式完成业务逻辑 三、为什么使用Spring? 前言 本文主要介绍Spring是什么,并且解释为何要去使用Spring&…...

自我监督学习日志
学习日志 10.12 一天学不了一分钟,不知道为什么也就是了 今天一定要学一个小时! 机器学习就是机器帮我们找一个函数 语音辨识,语音,声音讯号 转化为文字 帮我们找一个人类写不出来的复杂函数 类神经网络 输入 一张图片用一个矩…...

配置CA证书
前置条件 配置Java环境变量。 具体操作 windows环境 以管理员方式执行CMD窗口,输入命令; cd /d %JAVA_HOME%\jre\lib\securitycurl -kv https://xxx/artifactory/CMC-Release/certificates/xxxRootCA.cer -o xxxRootCA.cercurl -kv https://xxx/art…...

计算机毕业设计选什么题目好?springboot 高校就业管理系统
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...

上海-华为全联接大会|竹云受邀参加华为云ROMAConnect行业生态联盟成立联合发布会
2023年9月22日,在上海举办的华为全联接大会上,竹云作为华为云全方位合作伙伴代表,受邀参加华为云ROMAConnect行业生态联盟成立联合发布会。华为云PaaS服务产品部副部长张甲磊以及联盟主要成员企业出席发布仪式,共同见证华为云ROMA…...

走进GraalVM
是什么 GraalVM是一个高性能的JDK,旨在加速用Java和其他JVM语言编写的应用程序的执行,同时还为JavaScript,Python,Ruby和许多其他流行语言提供运行特点 GraalVM可以代替JDK、JVM之前的工作。 GraalVM除了支持Java,也支…...
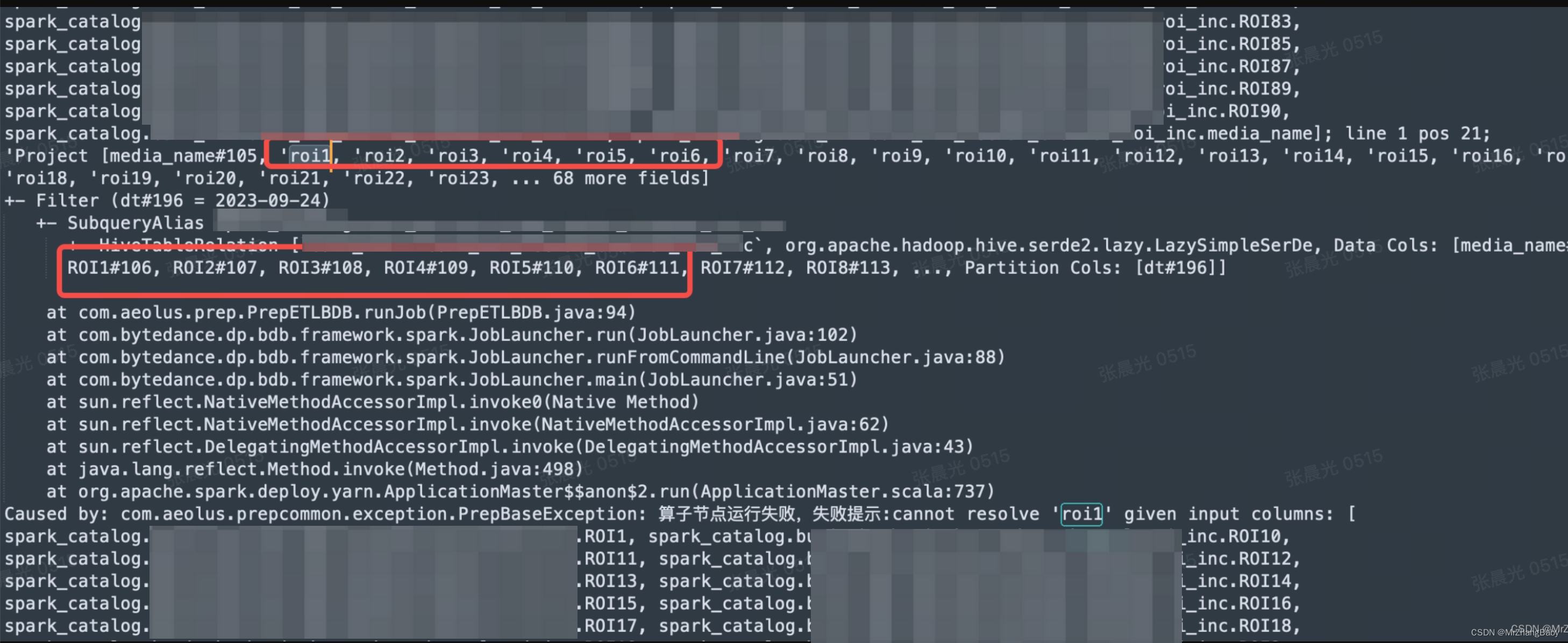
spark读取hive表字段,区分大小写问题
背景 spark任务读取hive表,查询字段为小写,但Hive表字段为大写,无法读取数据 问题错误: 如何解决呢? In version 2.3 and earlier, when reading from a Parquet data source table, Spark always returns null for any column …...
 和实现文件(.cpp)区别)
UE4和C++ 开发-头文件(.h) 和实现文件(.cpp)区别
.h文件和.cpp文件是C程序中的两种不同类型的文件。 .h文件通常包含类、函数和变量的声明, 而.cpp文件包含这些声明的实现。 .h文件中的声明通常是公共的,可以被其他文件包含和使用。.cpp文件中的实现通常是私有的,只能在该文件中使用。 在…...
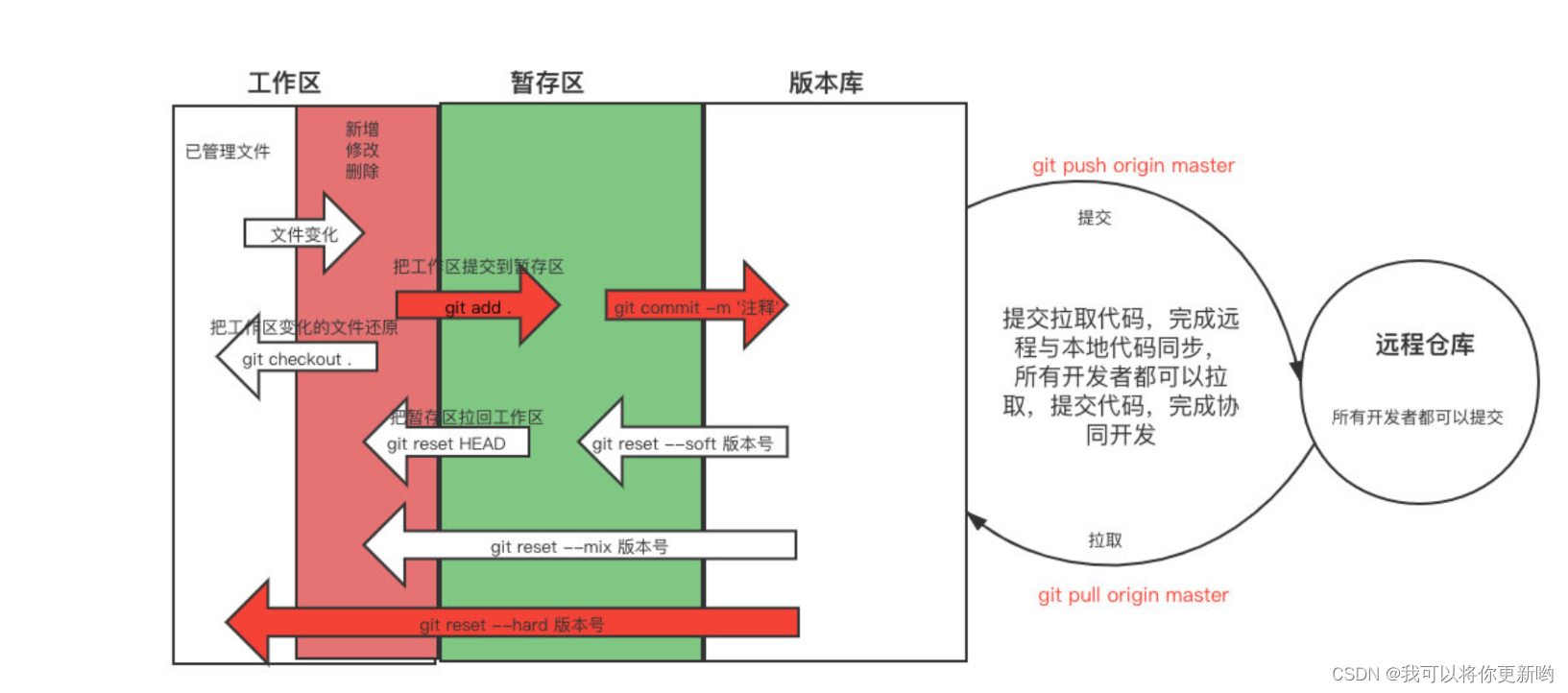
git介绍和安装、(git,github,gitlab,gitee介绍)、git工作流程、git常用命令、git忽略文件
1 git介绍和安装 2 git,github,gitlab,gitee介绍 3 git工作流程 4 git常用命令 5 git忽略文件 1 git介绍和安装 首页功能写完了---》正常应该提交到版本仓库---》大家都能看到这个---》 运维应该把现在这个项目部署到测试环境中---》测试…...

go cpu、内存监控、性能分析:PProf
PProf PProf 是什么 PProf是 golang 官方提供的性能调优分析工具,用于分析和优化Go程序的性能。 PProf通过收集和分析程序的运行时数据来生成性能分析报告。它使用Go语言的运行时特性,如代码注释和特殊的程序运行标记,来收集性能数据。PPr…...
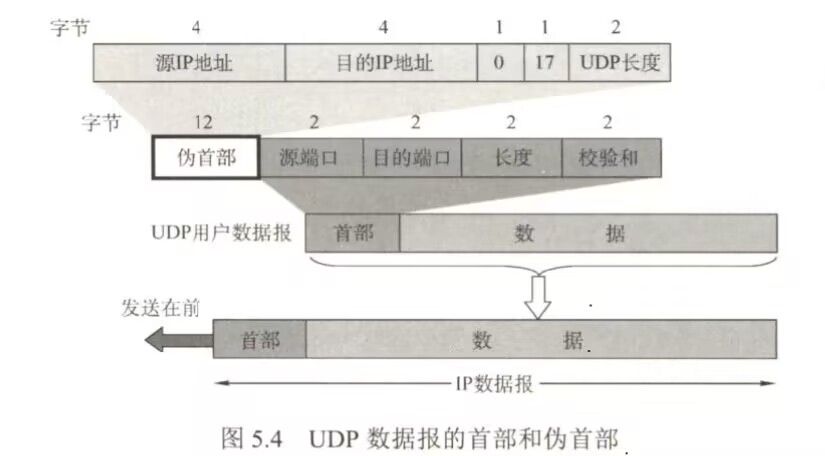
计算机网络传输层知识总结·
传输层提供的服务 传输层的功能 ●传输层提供进程之间的逻辑通信,即端到端的通信 ●复用和分用 ●差错检测(首部和数据部分) ●面向连接的TCP和无连接的UDP 端口的作用 ●端口标识的是主机中的进程 ●硬件端口是不同…...

vue使用ant design Vue中的a-select组件实现下拉分页加载数据
<a-form-model-item :labelCol"labelCol" :wrapperCol"wrapperCol" prop"equipmentTypeId" label"所属设备种类"> <a-select v-model"model.equipmentTypeId" popupScroll"handlePopupScroll" placehold…...

精准突击!GitHub星标103k,2023年整理1658页JAVA秋招面试题
前言: 现在的互联网开发岗招聘,程序员面试背八股文已经成为了不可逆转的形式,其中一个Java岗几百人在投简历也已经成为了常态!更何况一份面试题动辄七八百道,你吃透了,技术只要不是很差,面试怎…...
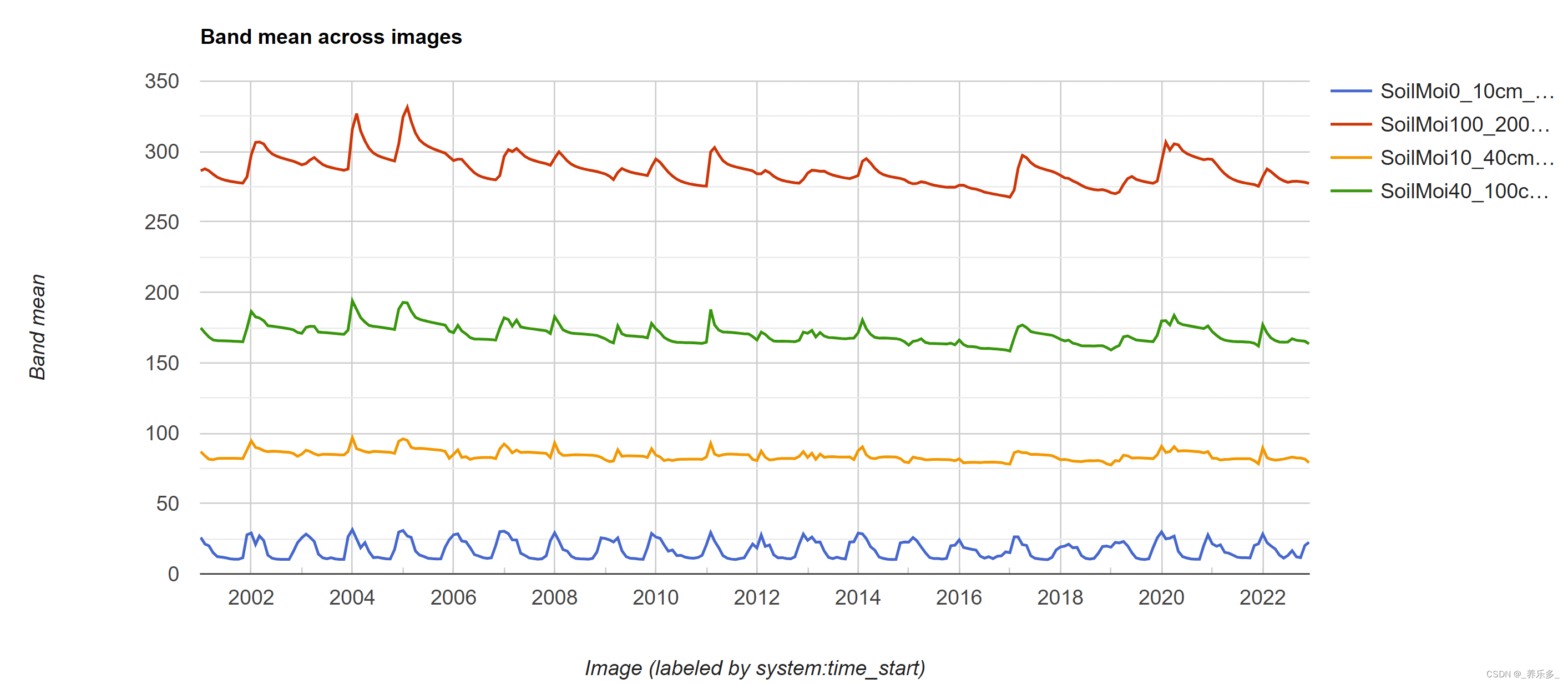
GEE:基于GLDAS数据集分析土壤湿度的时间序列变化
作者:CSDN @ _养乐多_ 本篇博客将介绍如何使用Google Earth Engine(GEE)进行土壤湿度数据的分析。我们将使用NASA GLDAS(Global Land Data Assimilation System)数据集,其中包括了关于土壤湿度的信息。通过该数据集,我们将了解土壤湿度在特定区域和时间段内的变化,并生…...
Nacos安装
Nacos安装 1.Windows安装 1.1.下载安装包 在Nacos的GitHub页面,提供有下载链接,可以下载编译好的Nacos服务端或者源代码: GitHub主页:https://github.com/alibaba/nacos GitHub的Release下载页:https://github.co…...
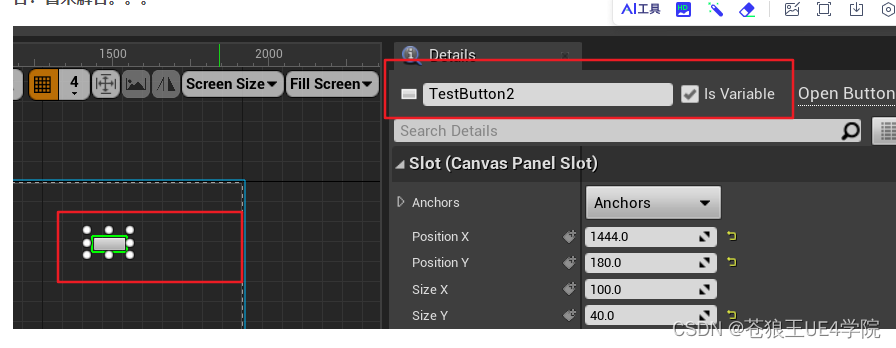
UE4和C++ 开发-C++与UMG的交互2(C++获取UMG的属性)
1、...C获取UMG的属性 1.1、第一种方法:通过名称获取控件。 void UMyUserWidget::NativeConstruct() {Super::NativeConstruct();//通过名字,获取蓝图控件中的按钮引用。CtnClic Cast<UButton>(GetWidgetFromName(TEXT("Button_44"))…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
