C++数位动态规划算法:统计整数数目
题目
给你两个数字字符串 num1 和 num2 ,以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件,我们称它是一个好整数:
num1 <= x <= num2
min_sum <= digit_sum(x) <= max_sum.
请你返回好整数的数目。答案可能很大,请返回答案对 109 + 7 取余后的结果。
注意,digit_sum(x) 表示 x 各位数字之和。
示例 1:
输入:num1 = “1”, num2 = “12”, min_num = 1, max_num = 8
输出:11
解释:总共有 11 个整数的数位和在 1 到 8 之间,分别是 1,2,3,4,5,6,7,8,10,11 和 12 。所以我们返回 11 。
示例 2:
输入:num1 = “1”, num2 = “5”, min_num = 1, max_num = 5
输出:5
解释:数位和在 1 到 5 之间的 5 个整数分别为 1,2,3,4 和 5 。所以我们返回 5 。
提示:
1 <= num1 <= num2 <= 1022
1 <= min_sum <= max_sum <= 400
分析
a. 先考虑数位相等
DoSameLen函数处理数位相等。用动态规划,假定已经处理了i位,正在处理第i位。对于某种状态,我们只关心:一,位数和,取值范围[0, max_sum],共max_sum+1种,大于max_sum的状态抛弃。二,上下界。非边界、上边界、下边界、上下界。如:num1=”121”,num2=”142”则”1”是上下界,"12"是下界,"13"是非边界、"14"是上边界。如果上下界,则当前位只能取值[num1[i],nums2[i]]。如果上边界,则只能取值[0,nums2[i]]。如果是下边界,则能取[nums1[i],9]。如果是非边界,则可以任意取值。
| 前一轮状态 | 当前条件 | 新状态 |
|---|---|---|
| 上下界 | 同时等于num1[i]和num2[i] | 上下界 |
| 上下界 | 等于num1[i] | 下界 |
| 上下界 | 等于num2[i] | 上界 |
| 上下界 | num1[i]和num2[i]之间 | 非边界 |
| 上界 | 等于num2[i] | 上界 |
| 上界 | 小于num2[i] | 非边界 |
| 下界 | 等于num1[i] | 下界 |
| 下界 | 大于num1[i] | 非边界 |
| 非边界 | 0到9 | 非边界 |
b. 优化掉上下界
上下界一定出现再最前面,且数量为1。当i为0时,有新的上下界,那说明num1[0]和num2[i],只能选择num1[i]。当i大于0是,有新的上下界,那么num1[i]等于num2[i],由于(i-1)也是上下界,所有num1和num2的前i+1个元素相同。由于第i为只能num1[i],所以数量不变。
假定num1和num2的前i位完全相同,则前i位只有一个合法数。
这意味这num1和num2扔掉相同的前者,边界状态的数量不变。比如:
num1 = “112”和num2 = “115”, 下界:115,非边界:113和114 上界:115。
num1 = “12”和num2 = “15”, 下界:15,非边界:13和14 上界:15。
num1 = “2”和num2 = “5”, 下界:5,非边界:3和4 上界:5。
c. 考虑数位不等
假定num1的长度为l1,num2的长度为l2,则分别:
Do(num1,string(l1,’9’)
for(int i = l1+1; i < l2 ;i++)
{
Do(‘1’+string(i-1,’0’),string(i,’9’);
}
Do(‘1’+string(i2-1,’0’),num2)
比如:
nums1 = “1”,nums2=”19”
Do(“1”,”9”)
Do(“10”,”19”)
再如:
nums1 = “1”,nums2=”123”
Do(“1”,”9”)
Do(“10,”99”)
Do(“100,”123”)
注意:
l1等于l2时要分别处理。
核心代码
class Solution {
public:
int count(string num1, string num2, int min_sum, int max_sum) {
m_min_sum = min_sum;
m_max_sum = max_sum;
const int l1 = num1.length();
const int l2 = num2.length();
if (l1 == l2)
{
return DoSameLen(num1, num2).ToInt();
}
C1097Int biRet;
biRet += DoSameLen(num1, string(l1, ‘9’));
for (int i = l1 + 1; i < l2; i++)
{
biRet += DoSameLen(“1” + string(i - 1, ‘0’), string(i,‘9’));
}
biRet += DoSameLen(“1” + string(l2-1,‘0’), num2);
return biRet.ToInt();
}
C1097Int<> DoSameLen(string num1, string num2)
{
int n = num1.size();//只处理相等位数
int i = 0;
int sum = 0;
for (; (i < n) && (num1[i] == num2[i]); i++)
{
sum += num1[i] - ‘0’;
}
if (i >= n)
{
return ((sum >= m_min_sum)&&( sum <= m_max_sum)) ? 1 : 0;
}
//注[1]
vector<vector<C1097Int<>>> pre(3, vector<C1097Int<>>(m_max_sum+1));
Set(pre, 1, sum + num1[i]-‘0’, 1);
for (int j = num1[i] + 1; j < num2[i]; j++)
{
Set(pre, 0, sum +j - ‘0’, 1);
}
Set(pre, 2, sum + num2[i] - ‘0’, 1);
for (i++; i < n; i++)
{
vector<vector<C1097Int<>>> dp(3, vector<C1097Int<>>(m_max_sum + 1));
for (int preSum = 0; preSum <= m_max_sum; preSum++)
{
//处理下界
Set(dp, 1, preSum + num1[i] - ‘0’, pre[1][preSum]);
for (int j = num1[i] + 1; j <= ‘9’; j++)
{
Set(dp, 0, preSum + j - ‘0’, pre[1][preSum]);
}
//处理无边界
for (int j = ‘0’; j <= ‘9’; j++)
{
Set(dp, 0, preSum + j - ‘0’, pre[0][preSum]);
}
//处理上界
for (int j = ‘0’; j < num2[i]; j++)
{
Set(dp, 0, preSum + j - ‘0’, pre[2][preSum]);
}
Set(dp,2, preSum + num2[i] - ‘0’, pre[2][preSum]);
}
pre.swap(dp);
}
return Cal(pre);
}
void Set(vector<vector<C1097Int<>>>& dp, int status, int sum,C1097Int<> iAddNum)
{
if (sum > m_max_sum)
{
return;
}
dp[status][sum] += iAddNum;
}
C1097Int<> Cal(const vector<vector<C1097Int<>>>& pre)
{
C1097Int<> biRet;
for (int i = 0; i < 3; i++)
{
for (int j = m_min_sum; j <= m_max_sum; j++)
{
biRet += pre[i][j];
}
}
return biRet;
}
int m_min_sum, m_max_sum;
};
测试代码
int main()
{
int res = 0;
res = Solution().count(“2”, “5”, 0, 100);
assert(res == 4);
res = Solution().count(“12”, “15”, 0, 100);
assert(res == 4);
res = Solution().count(“112”, “115”, 0, 100);
assert(res == 4);
res = Solution().count(“112”, “115”, 5, 100);
assert(res == 3);
res = Solution().count(“112”, “115”, 0, 6);
assert(res == 3);
res = Solution().count(“112”, “115”, 5, 6);
assert(res == 2);
res = Solution().count(“1”, “12”, 1, 8);
assert(res == 11);
CConsole::Out(res);
}

其它
视频课程
如果你觉得复杂,想从简单的算法开始,可以学习我的视频课程。
https://edu.csdn.net/course/detail/38771
我的其它课程
[https://edu.csdn.net/lecturer/6176]
(https://edu.csdn.net/lecturer/6176)
测试环境
win7 VS2019 C++17
相关下载
算法精讲《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653

相关文章:

C++数位动态规划算法:统计整数数目
题目 给你两个数字字符串 num1 和 num2 ,以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件,我们称它是一个好整数: num1 < x < num2 min_sum < digit_sum(x) < max_sum. 请你返回好整数的数目。答案可能很大&…...

ip 网段设置 --chatGPT
问:host all all 127.0.0.1/32 scram-sha-256 里的 127.0.0.1/32 是什么含义 ,要指定某个呢 gpt: 在 PostgreSQL 的 pg_hba.conf 文件中,127.0.0.1/32 是一个用于定义访问控制规则的CIDR(无类域间路由)标记࿰…...

使用JMeter进行接口测试教程
安装 使用JMeter的前提需要安装JDK,需要JDK1.7以上版本目前在用的是JMeter5.2版本,大家可自行下载解压使用 运行 进入解压路径如E: \apache-jmeter-5.2\bin,双击jmeter.bat启动运行 启动后默认为英文版本,可通过Options – Cho…...

文本生成解码策略
解码策略 1. sample实现了怎样的功能 不是直接选择概率最大的token,而是根据多项式分布进行采样获得下一个token 这里的概率通过设置一些策略,进行处理。例如,解码最小长度(当长度小于该值的时候,eos的采样概率为0&am…...
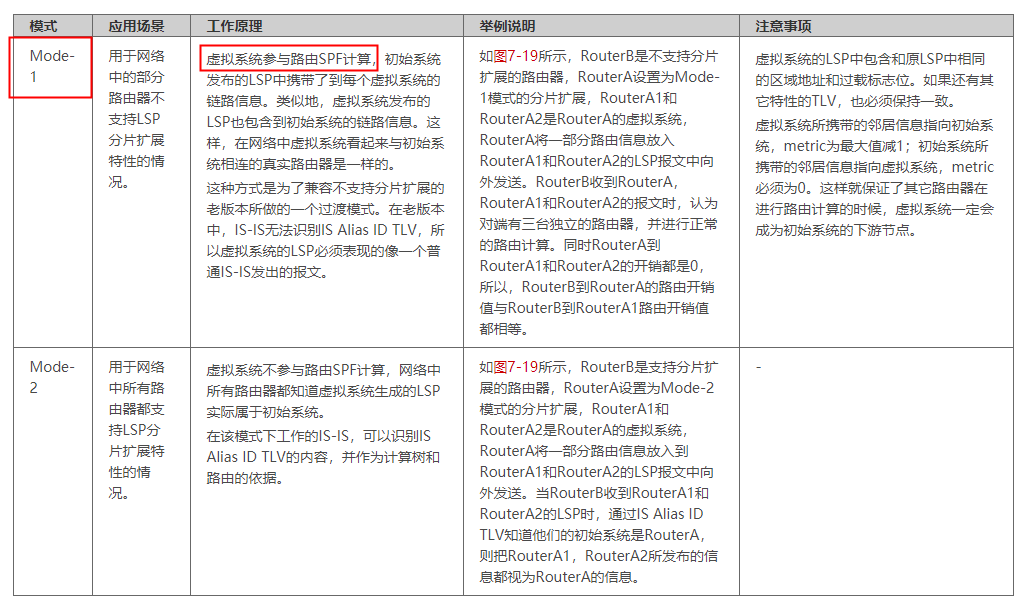
华为数通方向HCIP-DataCom H12-831题库(单选题:221-240)
第221题 以下关于IS-IS的LSP分片功能的描述,正确的是哪一项? A、IS-IS的分片扩展功能的Mode-1模式,虚拟系统是需要参与路由SPF计算的 B、IS-IS的LSP分片功能,是用于让收到LSP分片报文的设备老化相关路由信息 C、IS-IS的分片扩展功能,是通过LSP报文中的LSPID实现的 D、IS-…...

AttributeError: module ‘hanlp.utils.rules‘ has no attribute ‘tokenize_english‘
附原文链接:http://t.csdnimg.cn/wVLib import hanlp tokenizer hanlp.utils.rules.tokenize_english tokenizer(Mr. Hankcs bought hankcs.com for 1.5 thousand dollars.) 改为: from hanlp.utils.lang.en.english_tokenizer import tokenize_eng…...

苍穹外卖(四) AOP切面公共字段自动填充及文件上传
一.AOP切面公共字段填充 问题分析 如果都按照上述的操作方式来处理这些公共字段, 需要在每一个业务方法中进行操作, 编码相对冗余、繁琐,那能不能对于这些公共字段在某个地方统一处理,来简化开发呢? 答案是可以的,我们使用AOP切…...

vue-cli + vue3 项目 ios 苹果手机白屏问题
目录 问题描述原因分析解决方案遇到的坑1,架构问题2,项目引入其他依赖的问题 参考 问题描述 vue-cli vue3 的项目,在苹果手机上打开白屏,安卓手机正常显示。 原因分析 1,借助 vconsole 发现并没有打印报错信息&…...

Spring Boot中的JdbcTemplate是什么,如何使用
Spring Boot中的JdbcTemplate是什么,如何使用 Spring Boot是一个流行的Java应用程序开发框架,它简化了Java应用程序的开发过程,并提供了丰富的功能和工具。在Spring Boot中,JdbcTemplate是一个强大的数据库访问工具,它…...

Python测网络连通性、能否访问某个网络或者端口号<网络检测、ping主机、测试端口>
一、ping命令及其使用 ping命令是在计算机网络领域中用来测试目标主机是否可达以及其延迟时间的命令。对于Python来说,我们可以通过subprocess模块来实现执行命令。下面是示例代码: import subprocessdef ping(host):result subprocess.run([ping, -c…...

【沧元图】玉阳宫主是正是邪,和面具人有勾结吗?现在已有答案了
Hello,小伙伴们,我是小郑继续为大家深度解析沧元图。 沧元图这部动漫中,有一个很特殊的人物,也是一个让人看不透的人物,因为很多人都不知道这个人是正还是邪,这个人就是玉阳宫主。 因为这个人明面上是掌管东宁府维护东…...
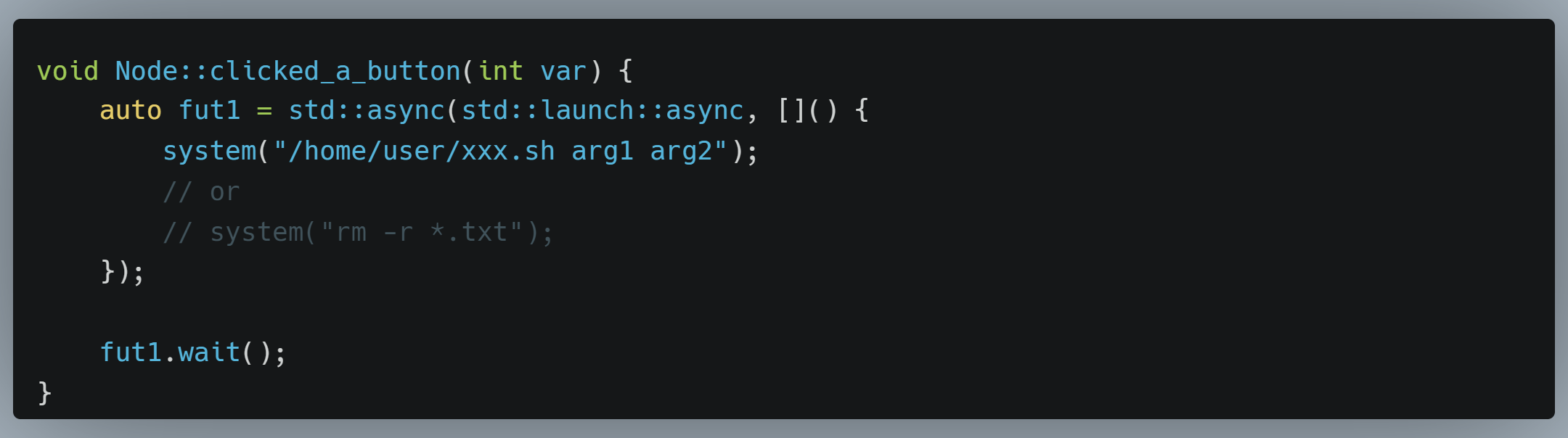
C++笔记之popen()和std_system()和std_async()执行系统命令比较
C笔记之popen()和std_system()和std_async()执行系统命令比较 code review! 文章目录 C笔记之popen()和std_system()和std_async()执行系统命令比较1.popen()2.std::system()3.std::async()——C11提供的异步操作库,适合在多线程中执行外部命令,建议使…...
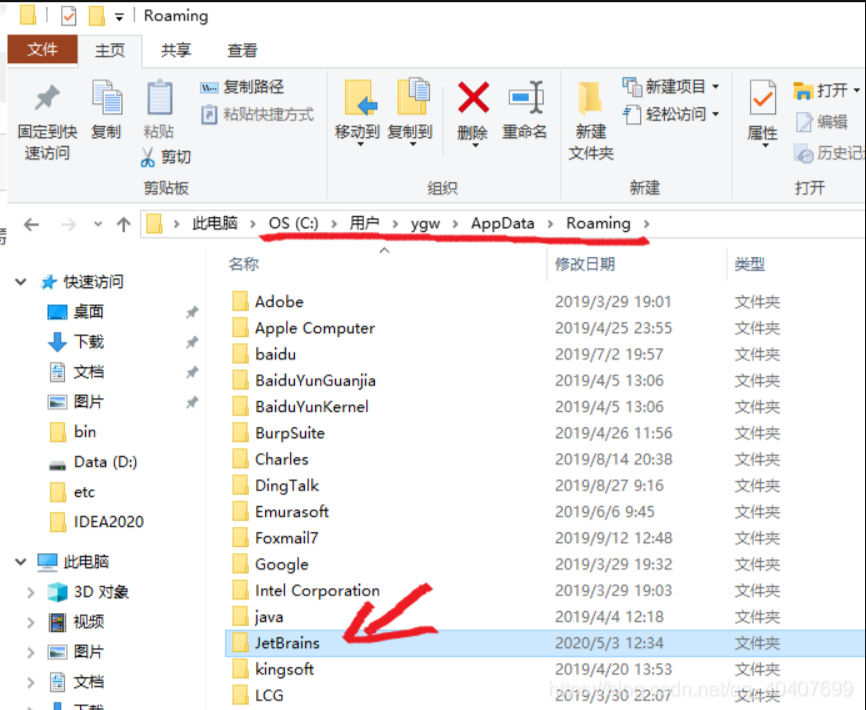
pycharm2020无法打开,点击无反应
pycharm 2020 无法打开,点击无反应,今天我碰到这现象,总结大体原因 C:\Users\ygw\AppData\Roaming\JetBrains (删除该目录即可,一般由于升级安装 或 安装两个不同版本 会存在老旧文件影响导致)...
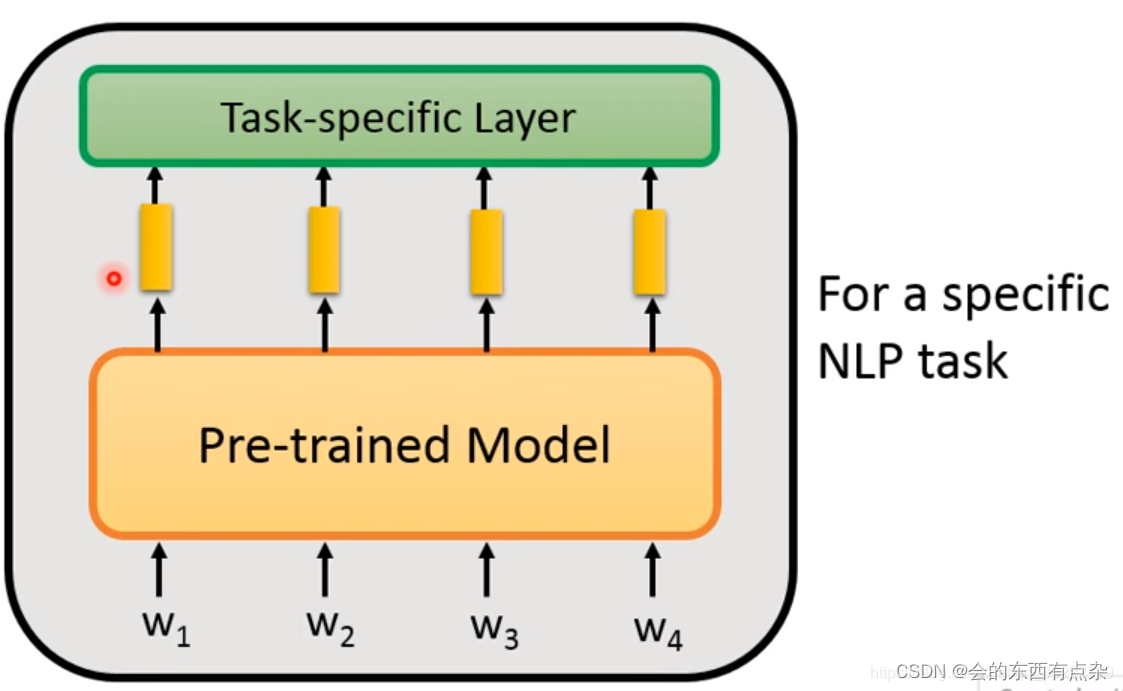
深度学习之微调
在现代深度学习领域,精细调整(Fine-tune)已经成为一种非常重要的技术手段。 预训练模型 在介绍finetune之前,先了解一下什么是预训练模型。在搭建一个网络模型来完成一个特定的图像分类的任务时,首先,需要…...

【# 完美解决 node.js 模块化后报错 ReferenceError: require is not defined】
完美解决 node.js 模块化后报错 ReferenceError: require is not defined 错误信息如图 直接改插件源码:(不是cnpm里的插件,而是下载下来的export2Excel.js) 在export2Excel.js内只要改动头部一行源码即可 改之前:…...

Jackson忽略json数组中null元素
问题 前端传过来的json字符串中,其中json数组包含null字符。类型如下: ["0","1","2",null]这边Spring使用Jackson进行反序列化是会出现List对象中,包含null的数组元素。即List大小为4,本来List的…...
基于SpringBoot的网上订餐系统
基于SpringBoot的网上订餐系统的设计与实现 开发语言:Java数据库:MySQL技术:SpringBootMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 【主要功能】 角色:用户、管理员管理员:登录、个人中心、会员管理、…...

【04】基础知识:React组件实例三大核心属性 - state
一、state 了解 理解 1、state 是组件对象最重要的属性,值是对象(可以包含多个 key-value 的组合) 2、组件被称为 “状态机”, 通过更新组件的 state 来更新对应的页面显示(重新渲染组件) 强烈注意 1、…...
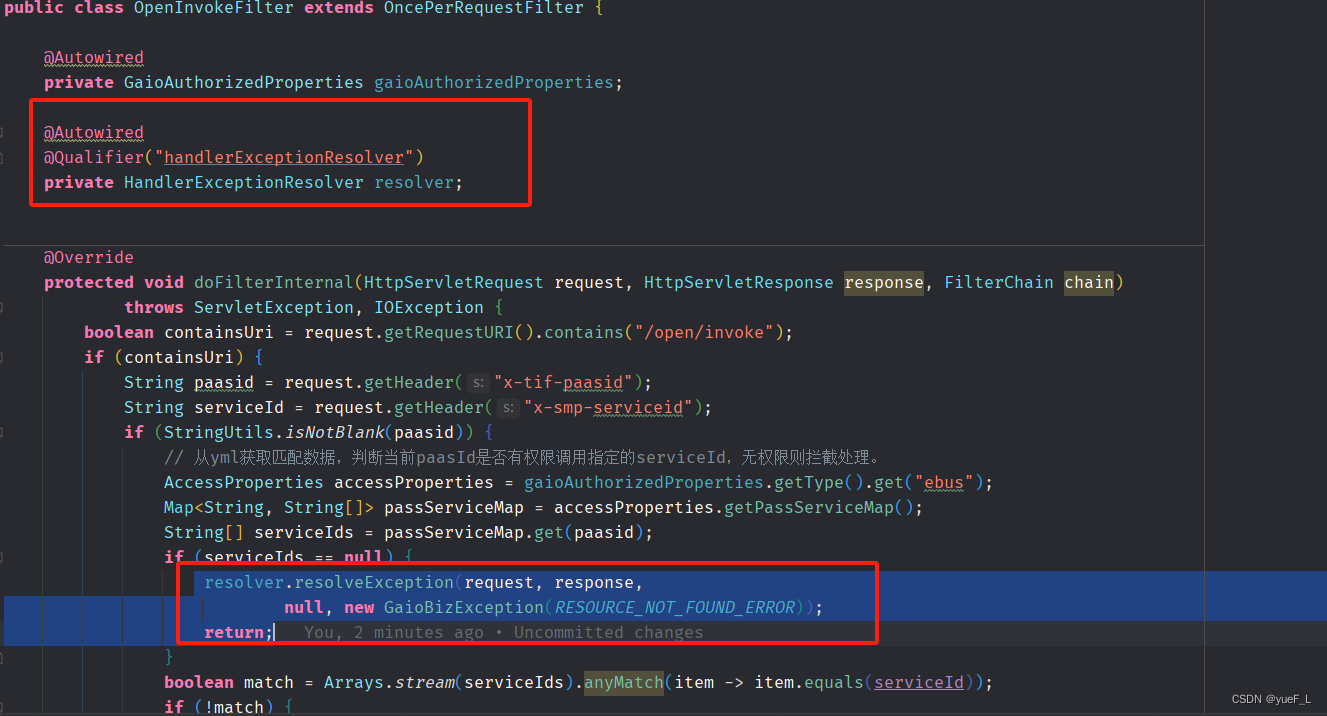
SpringBoot 过滤器filter当中的自定义异常捕获问题
需求描述:需要根据用户的请求路径拦截做权限控制: 但是这样做全局异常无法捕获 解决方案: 在filter当中引入HandlerExceptionResolver类,通过该类的resolveException方法抛出自定义异常: public class OpenInvokeFil…...
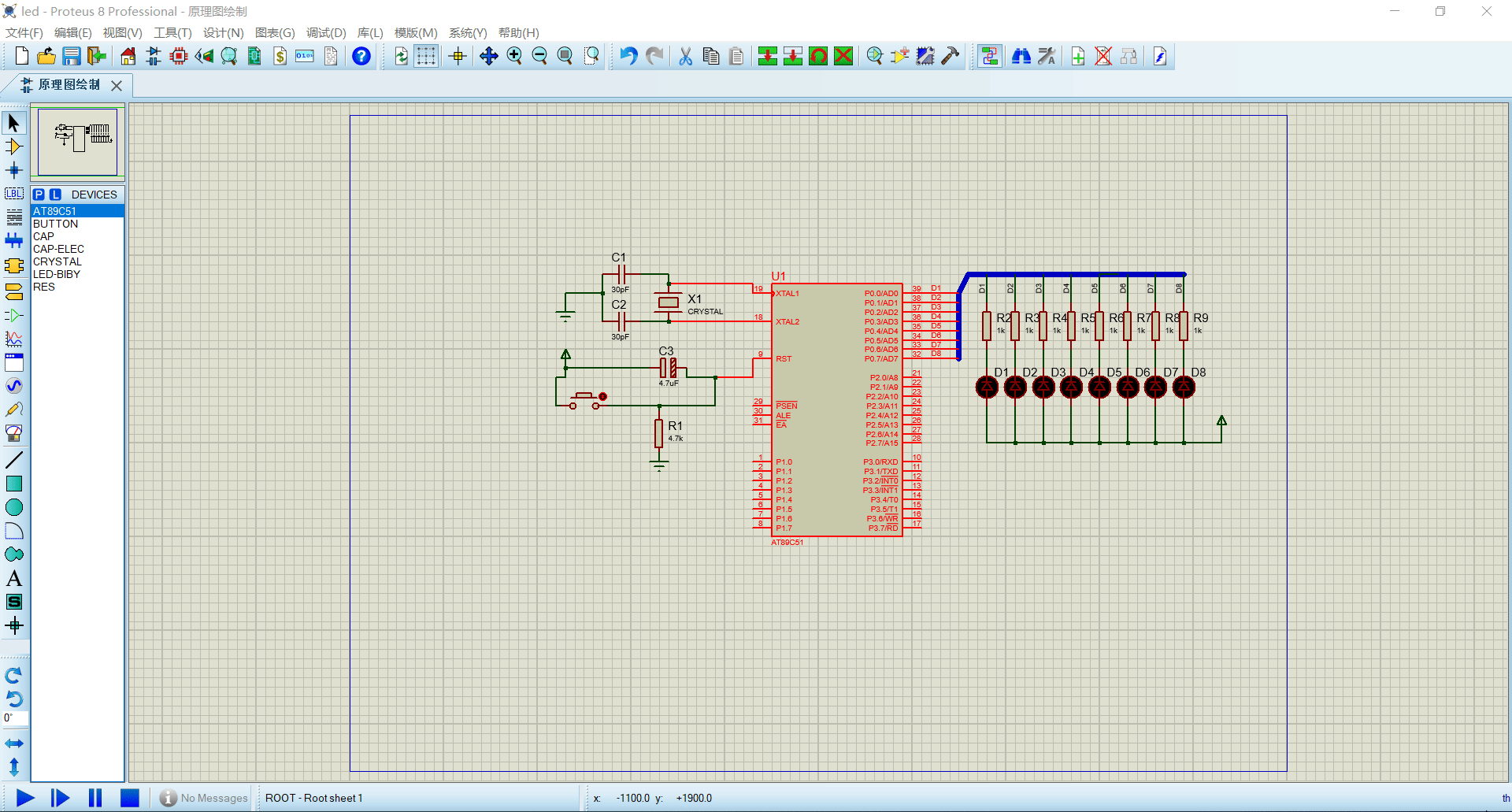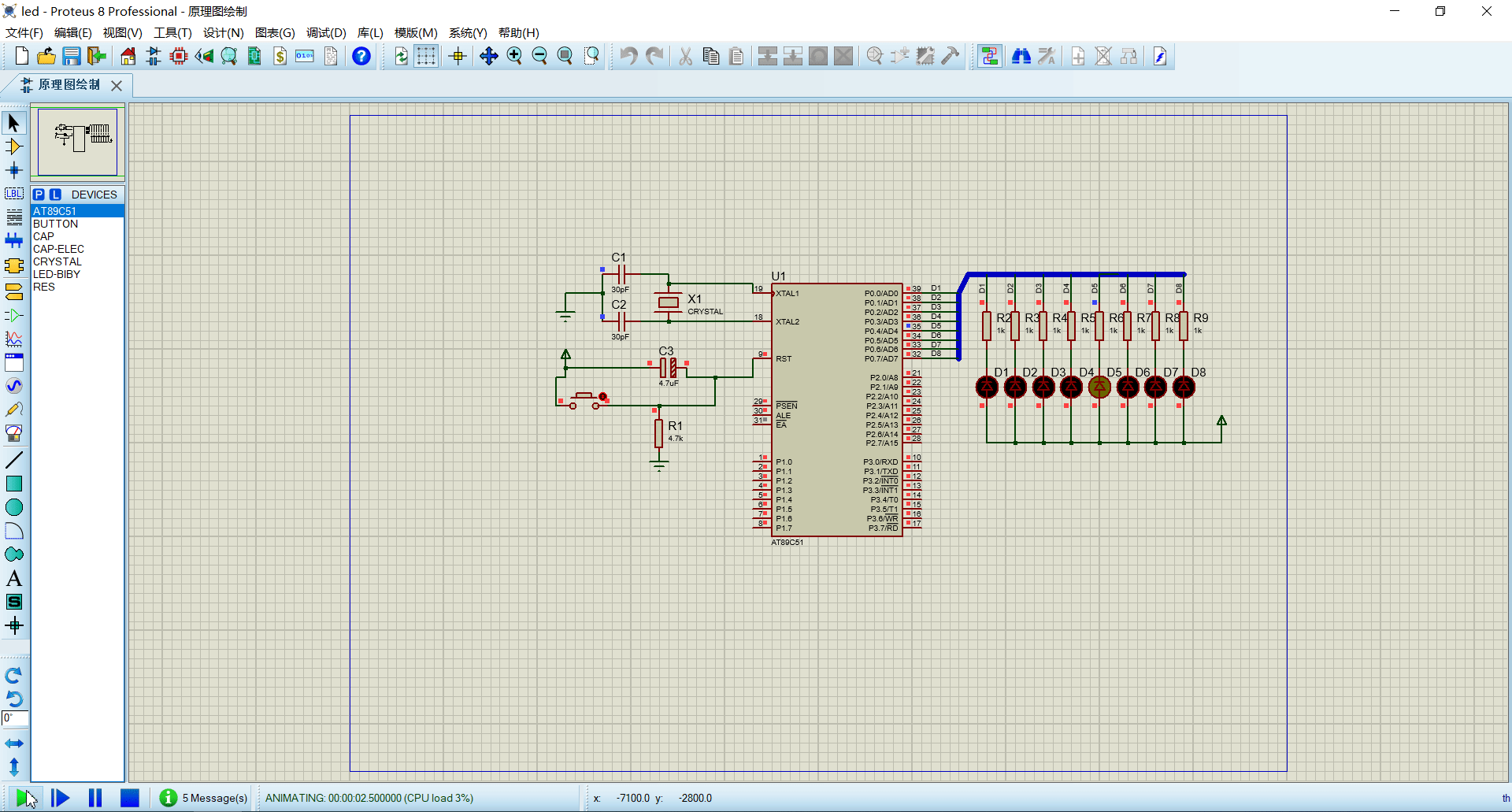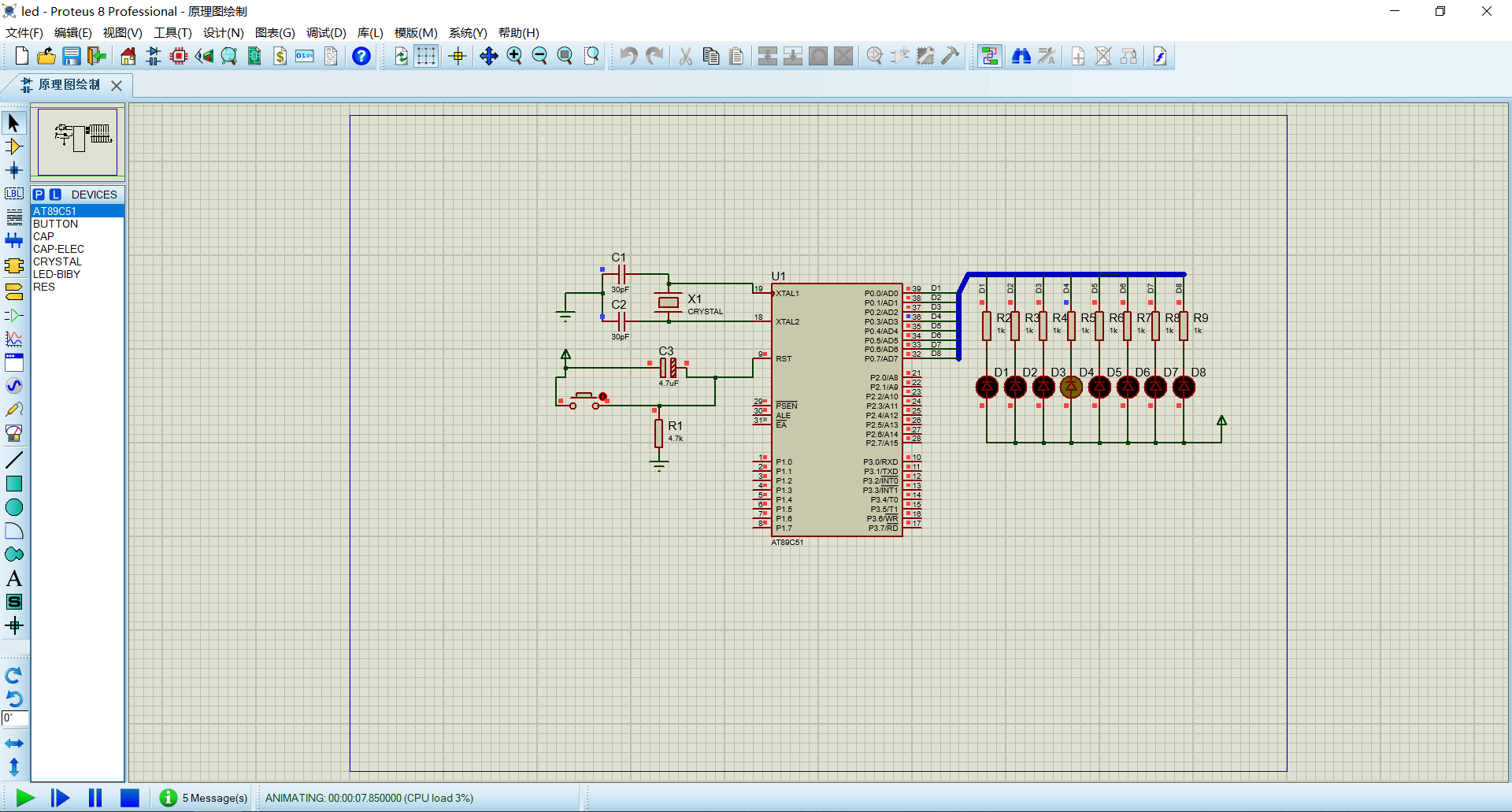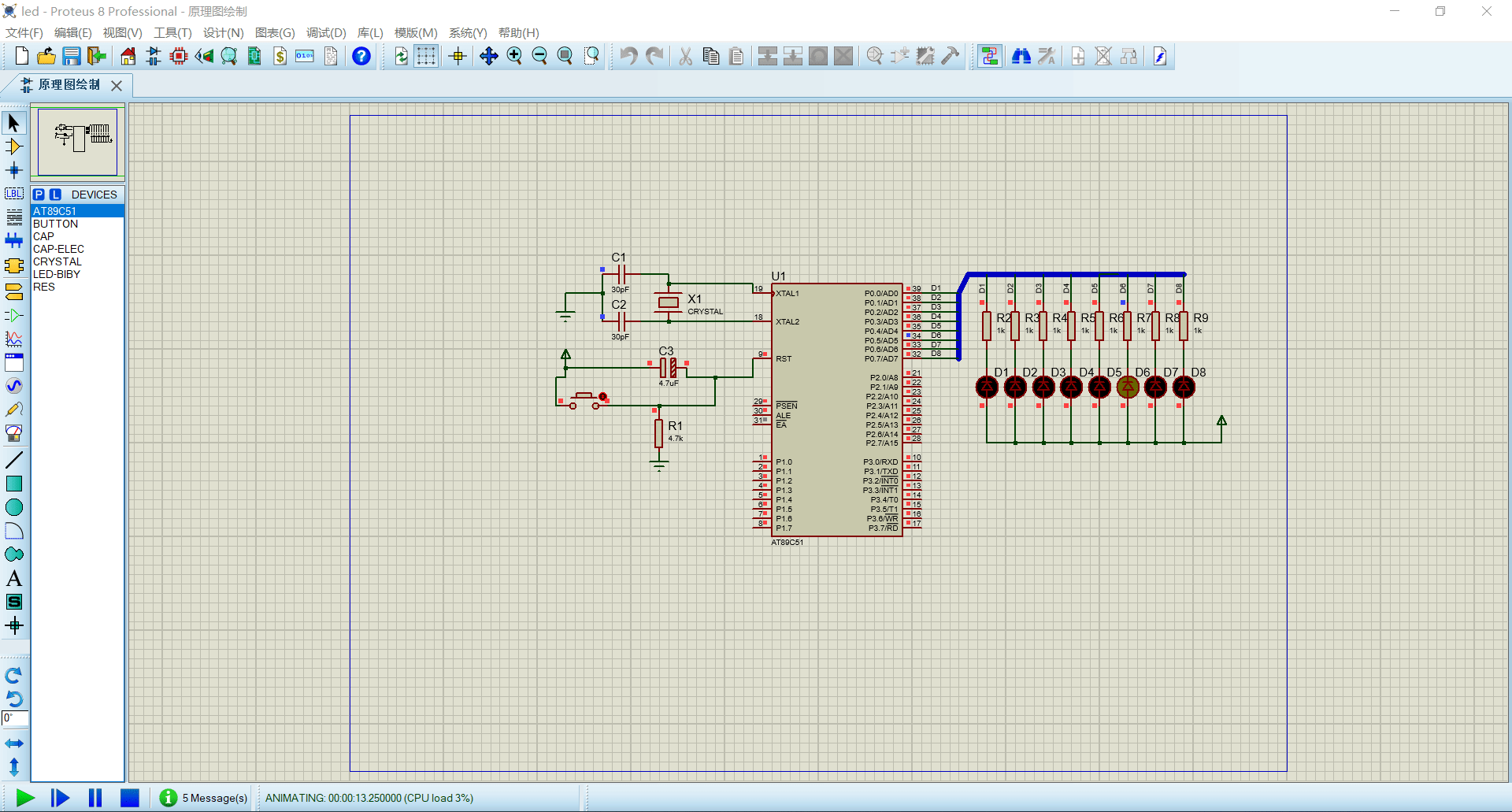
实验3:左右循环LED灯
获取流水灯工程: 方式一: keilproteus 完成最小系统,点亮led 灯实验_吴小凹的博客-CSDN博客 方式二: Flowing_led.zip - 蓝奏云直接下载。 原理图修改: 无须修改只需要使用流水灯的工程即可,解压到桌面…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
