课题学习(八)----卡尔曼滤波动态求解倾角、方位角
一、 卡尔曼滤波
卡尔曼滤波的应用要求系统和底层过程的测量模型都是线性的。离散时间线性状态空间系统的描述为: x k = Φ k , k − 1 x k − 1 + G k − 1 w k − 1 x_k=\Phi_{k,k-1}x_{k-1}+G_{k-1}w_{k-1} xk=Φk,k−1xk−1+Gk−1wk−1
式中 Φ k , k − 1 \Phi_{k,k-1} Φk,k−1为状态转移矩阵, x k x_k xk为状态向量, G k − 1 G_{k-1} Gk−1为噪声分布矩阵, w k − 1 w_{k-1} wk−1为过程噪声向量,k为测量历元。
系统的测量方程由下式给出 z k = H k x k + η k z_k=H_kx_k+\eta_k zk=Hkxk+ηk
式中 z k z_k zk为系统输出的测量向量, H k H_k Hk为观测或设计, η k \eta_k ηk为测量噪声。系统噪声w和测量噪声 η k \eta_k ηk是具有确定的自协方差函数的非相关零均值白噪声过程。
通过对钻柱动力学的分析,提出了一种新的状态空间模型算法。在计算方法中,我们定义KF-1的输入矢量为 X = [ a x a y a z m x m y m z ] X=\begin{bmatrix}a_x&a_y&a_z\\ m_x&m_y&m_z\end{bmatrix} X=[axmxaymyazmz],由三轴磁强计和三轴加速度计测量。KF-2的输入向量为井眼倾角和方位角,定义为 X = [ I A ] X=\begin{bmatrix}I\\ A\end{bmatrix} X=[IA],其中 I I I为井眼倾角, A A A为井眼方位角。
求解过程如下图所示:

在此过程中,设计两个卡尔曼滤波器。在KF-1之后,我们可以得到更精确的重力加速度信号gx, gy和gz,定义为KF-1的输出。利用重力加速度,通过建立钻柱旋转时的方程,可以得到钻柱的倾角和方位角。然后使用KF-2进一步平滑钻井轨迹。KF-2的输出定义为 M ′ = [ I ′ A ′ ] T M'=\begin{bmatrix}I'&A'\end{bmatrix}^T M′=[I′A′]T,这是更精确的。
1.1 KF-1的状态空间模型
传感器安装在钻柱的中心,在旋转过程中,x轴和y轴的测量信号呈现正弦波。理论上,加速度计和磁力计的信号有相同的规律。在实际钻井过程中,钻柱的振动对磁强计信号的影响较小。也就是说,磁力计信号是用来校准加速度计信号的。通过实验室测试,我们可以得出磁通门信号的变化与重力加速度信号的变化是一致的。
假设角速度为 w x , y , z w_{x,y,z} wx,y,z,采样间隔为Δt,则
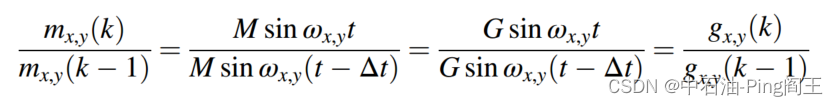
在KF-1中,我们将状态向量定义为 X = [ g x ( k ) g y ( k ) g z ( k ) ] X=\begin{bmatrix}g_x{(k)}\\g_y{(k)}\\g_z{(k)}\end{bmatrix} X= gx(k)gy(k)gz(k) ,从 a x , a y , a z a_x,a_y,a_z ax,ay,az的振动信号可以得到重力加速度信号 x g ( k ) x_g{(k)} xg(k)。因此,系统输出的测量矢量为,当钻柱旋转时,除了z轴信号外,x轴和y轴的测量信号将呈现正弦波。因此,变换矩阵定义为 z ( k ) = [ a x a y a z ] z(k)=\begin{bmatrix}a_x\\a_y\\a_z\end{bmatrix} z(k)= axayaz , H k = [ m x ( k − 1 ) m x ( k ) 0 0 0 m y ( k − 1 ) m y ( k ) 0 0 0 1 ] H_k=\begin{bmatrix}\frac{m_x{(k-1)}}{m_x{(k)}}&0&0\\ 0&\frac{m_y{(k-1)}}{m_y{(k)}}&0\\ 0&0&1\end{bmatrix} Hk= mx(k)mx(k−1)000my(k)my(k−1)0001 。系统噪声 w k w_k wk和测量噪声 η k \eta_k ηk是不相关的零均值白噪声过程。因此,我们得到KF-1的状态空间模型如下: x g ( k ) = [ m x ( k − 1 ) m x ( k ) 0 0 0 m y ( k − 1 ) m y ( k ) 0 0 0 1 ] x g ( k − 1 ) + [ w x ( k − 1 ) w y ( k − 1 ) w z ( k − 1 ) ] x_g{(k)}=\begin{bmatrix}\frac{m_x{(k-1)}}{m_x{(k)}}&0&0\\ 0&\frac{m_y{(k-1)}}{m_y{(k)}}&0\\ 0&0&1\end{bmatrix}x_g{(k-1)+\begin{bmatrix}w_x{(k-1)}\\w_y{(k-1)}\\w_z{(k-1)}\end{bmatrix}} xg(k)= mx(k)mx(k−1)000my(k)my(k−1)0001 xg(k−1)+ wx(k−1)wy(k−1)wz(k−1)
z ( k ) = H k x g ( k ) + η ( k ) z(k)=H_kx_g{(k)}+\eta(k) z(k)=Hkxg(k)+η(k)
1.2 计算倾角和方位角
钻柱旋转时,上述方程不适用。安装在钻柱中心的传感器,即x轴和y轴的测量信号,在旋转过程中呈现正弦波。
通过KF-1,我们得到gx、gy和gz,它们分别定义为x、y和z轴上的重力加速度测量信号。然后定义系统的输入向量为 X ′ = [ g x g y g z m x m y m z ] X'=\begin{bmatrix}g_x&g_y&g_z\\ m_x&m_y&m_z\end{bmatrix} X′=[gxmxgymygzmz]。
定义转速为R,若R为0,则用下式计算倾角和方位角。
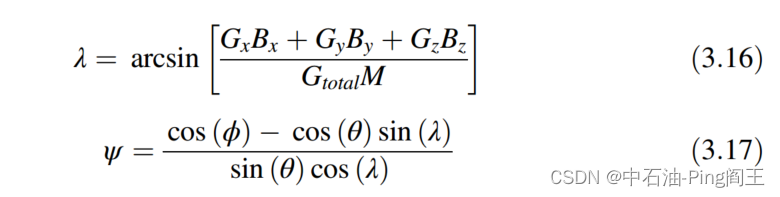
R ≠ 0 R\neq0 R=0表示钻柱在旋转,倾角I和方位角A的计算公式如下:
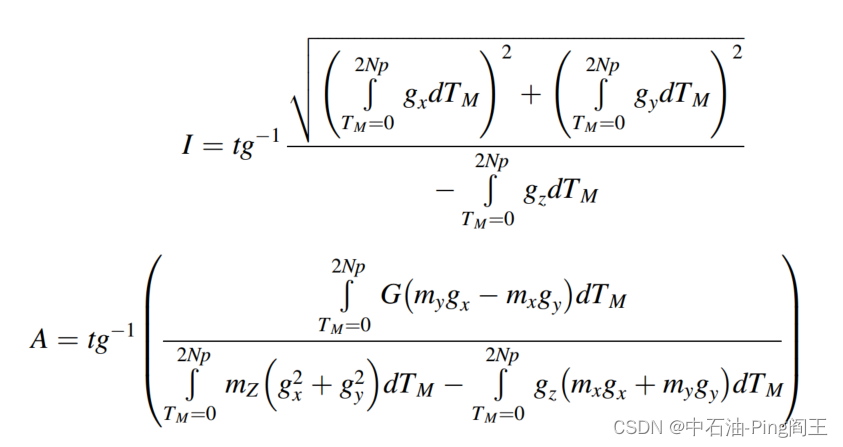
式中 T M T_M TM为磁性工具面角: T M = t g − 1 ( − m y m x ) T_M=tg^-1(\frac{-m_y}{m_x}) TM=tg−1(mx−my)。用于近直井的工具面角。磁性工具面是在垂直于井筒轴线的平面上,顺时针方向测量的井眼测量仪器在井筒内的角度或方位角;北、东、南、西方向的磁性工具面角分别为0°、90°、180°和270°。磁性工具面可以校正为参考栅格北或真北。
虽然钻柱转速是判断钻柱是否旋转的一种方法,但这种方法的可靠性不高。相反,使用标准差统计方法来确定钻柱的运动更加可靠,因为它反映了群体中个体之间的分散程度。使用50个数据点作为时间窗口,假设它们是x1, x2,…, x49, x50,我们得到标准差 σ = 1 N ∑ i = 1 N ( x i − x ˉ ) 2 \sigma=\sqrt{\frac{1}{N}\sum_{i=1}^N(x_i-\bar{x})^2} σ=N1∑i=1N(xi−xˉ)2,当标准差σ接近于零时,钻柱可以认为是静止的。
1.3 KF-2的状态空间模型
在钻孔过程中,运动状态为 σ = 0 \sigma=0 σ=0和 σ ≠ 0 \sigma\neq0 σ=0交替出现。当 σ ≠ 0 \sigma\neq0 σ=0时,由于钻柱不旋转时振动较小,求解结果更为准确。我们开发了另一种卡尔曼滤波器(KF-2)来平滑钻井轨迹。(KF-2分别分为KF-2.1和KF2.2,如下图所示。)
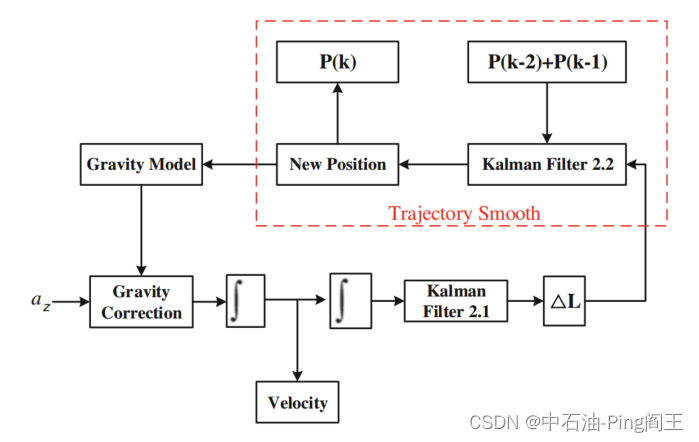
在正常的钻井过程中,为了测量倾角和方位角,钻井作业经常要停在测量站。然后根据数学假设计算两个测量站之间的井眼轨迹。例如,可以假设钻孔距离为直线、圆弧或多角线;每个都需要不同的计算方法。设实际钻井轨迹测量第N点的三维坐标为 ( x N , y N , z N ) (x_N,y_N,z_N) (xN,yN,zN),则测量(N +1)点为 ( x N + 1 , y N + 1 , z N + 1 ) (x_{N+1},y_{N+1},z_{N+1}) (xN+1,yN+1,zN+1),井深、垂深、倾角、方位角分别为 L N 、 H N 、 θ N 、 Ψ N L_N、H_N、\theta_N、\Psi_N LN、HN、θN、ΨN和$L_{N+1}、H_{N+1}、\theta_{N+1}、\Psi_{N+1}。两点之间的井眼轨迹定义如下:

如果垂直深度H已知,则测量(N + 1)-th点的三维坐标可定义为
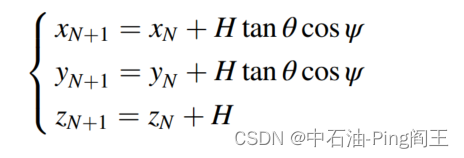
我们可以通过递归计算得到每个点的空间坐标,从而得到整个钻井轨迹。如下图所示,我们可以使用井眼轨迹外推法建立相邻两个测点之间的递推关系。
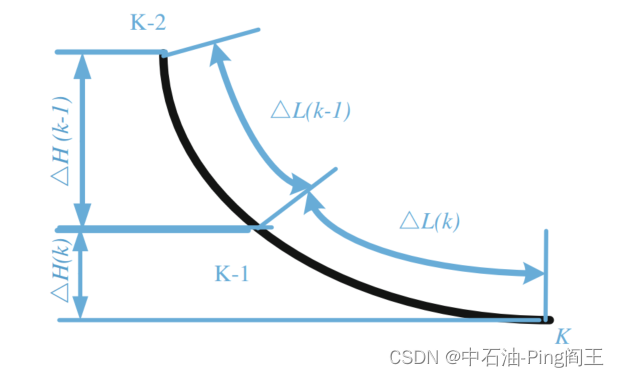
假设L是钻孔深度, γ \gamma γ是钻孔轨迹与其切线的夹角,然后: L ( k ) = L ( k − 1 ) + Δ L ( K ) L(k)=L(k-1)+\Delta L(K) L(k)=L(k−1)+ΔL(K)
γ = a r c c o s [ c o s ( I k − 2 ) c o s ( I k − 1 ) + s i n ( I k − 2 ) s i n ( I k − 1 ) c o s ( A k − 1 − A k − 2 ) ] \gamma=arccos[cos(I_{k-2})cos(I_{k-1})+sin(I_{k-2})sin(I_{k-1})cos(A_{k-1}-A_{k-2})] γ=arccos[cos(Ik−2)cos(Ik−1)+sin(Ik−2)sin(Ik−1)cos(Ak−1−Ak−2)]
γ ( k ) = γ Δ L ( k − 1 ) Δ L ( k ) \gamma(k)=\frac{\gamma}{\Delta L(k-1)}\Delta L(k) γ(k)=ΔL(k−1)γΔL(k)
从上面三个公式看出,我们可以使用两个点来估计下一个点,因此可以平滑井眼轨迹。我们可以使用Kalman Filter 2.2对钻井轨迹进行校准,其中将第k个测量点定义为 P ( k ) = [ I k A k ] P(k)=[I_k A_k] P(k)=[IkAk]。系统输入为P(K -2)和P(K -1), KF-2.2结合实测值和理论计算值估算P(K)。
KF-2.2通过倾角和方位角作为输入,实现井眼轨迹平滑。假设状态向量为 x ( k ) = [ I k A k ] x(k)=\begin{bmatrix}I_k\\A_k\end{bmatrix} x(k)=[IkAk],则系统输出的测量向量为 x ( k ) = [ I k A k ] m x(k)=\begin{bmatrix}I_k\\A_k\end{bmatrix}_m x(k)=[IkAk]m, H ( k ) = [ 1 0 0 1 ] H(k)=\begin{bmatrix}1&0\\0&1\end{bmatrix} H(k)=[1001]。得到KF-2.2的状态空间模型:
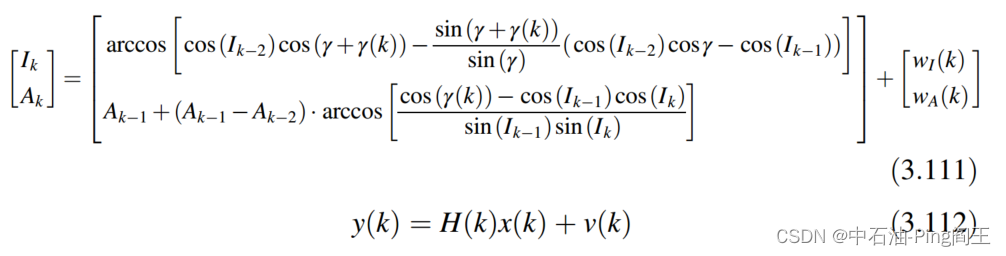
如上所示,我们应该确定 Δ L \Delta L ΔL作为KF-2.2的输入。( Δ t \Delta t Δt期间钻头向前移动的距离)。我们可以通过测量z轴上的加速度来计算位移。 A z A_z Az是z轴上三轴加速度计的信号,它与重力加速度和振动加速度相结合。定义加速度在z轴时间序列上的测量为 a z ( k ) a_z(k) az(k)。
所以在计算位移 Δ L \Delta L ΔL之前,我们首先要排除重力的影响,如下所示: f g z ( k ) = a z ( k ) − G ⋅ c o s ( I k − 1 ) f_{g_z}(k)=a_z(k)-G·cos(I_{k-1}) fgz(k)=az(k)−G⋅cos(Ik−1)
其中 f g z ( k ) f_{g_z}(k) fgz(k)是加速度时间序列函数,通过去掉 g z g_z gz的加速度,可以计算出 a z ( k ) a_z(k) az(k)和倾角 I k − 1 I_{k-1} Ik−1对应的同一时间。
然后我们可以使用z轴时间序列 f g z ( k ) f_{g_z}(k) fgz(k)上的加速度来计算钻探深度( Δ L \Delta L ΔL)。将状态向量定义为 Δ L ( k ) = [ Δ L ( k ) Δ L ˙ ( k ) Δ L ¨ ( k ) ] \Delta L(k)=\begin{bmatrix}\Delta L(k)\\\Delta \dot L(k)\\\Delta \ddot L(k)\end{bmatrix} ΔL(k)= ΔL(k)ΔL˙(k)ΔL¨(k) ,系统输出的测量向量为 z ( k ) = f g z ( k ) z(k)=f_{g_z}(k) z(k)=fgz(k),我们建立了KF-2.1的状态空间模型如下:
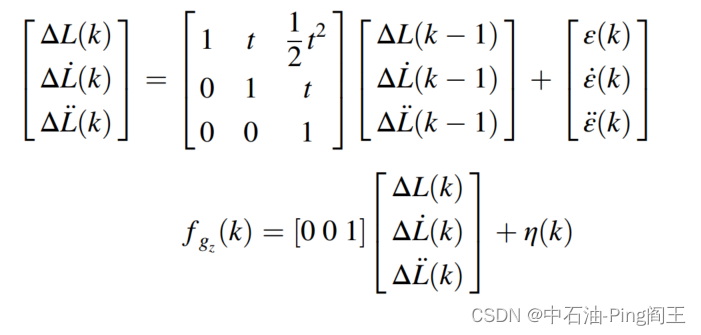
通过对实测信号进行预处理,建立了一种基于底部旋转钻具动力学分析的动态方位和倾角求解算法。在理论模型的基础上,我们开发了一种卡尔曼滤波器来提高求解器的精度;在预测钻井轨迹的基础上,建立了卡尔曼滤波的状态空间方程。基于卡尔曼滤波的动态测量算法是一种能够大大降低求解误差的新模型。
二、 往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
课题学习(七)----粘滑运动的动态算法
相关文章:
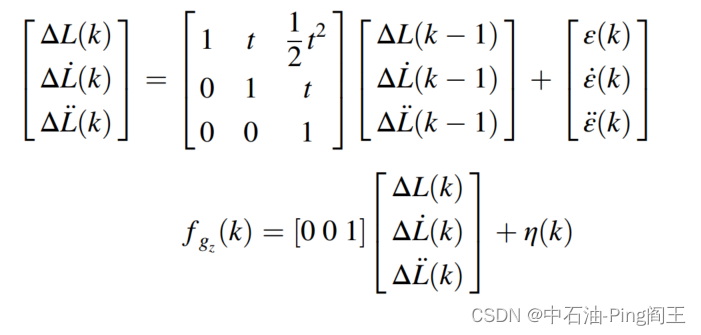
课题学习(八)----卡尔曼滤波动态求解倾角、方位角
一、 卡尔曼滤波 卡尔曼滤波的应用要求系统和底层过程的测量模型都是线性的。离散时间线性状态空间系统的描述为: x k Φ k , k − 1 x k − 1 G k − 1 w k − 1 x_k\Phi_{k,k-1}x_{k-1}G_{k-1}w_{k-1} xkΦk,k−1xk−1Gk−1wk−1 式中 Φ k , k − 1 \Phi_{…...
仿真软件Proteus8.9 SP2 Pro 下载、安装、汉化详细图文教程
Proteus8.9 安装教程 视频教程一、安装软件解压二、软件安装常见问题及解决方法:三、汉化 Proteus8.9 SP2 Pro 安装教程 本破解教程仅供个人及 proteus 8.9粉丝们交流学习之用,请勿用于商业用途, 谢谢支持。此版本为Proteus8.9 SP2 Pro。其他…...

振弦传感器和无线振弦采集仪在隧道安全监测的解决方案
振弦传感器和无线振弦采集仪在隧道安全监测的解决方案 隧道作为交通工程的重要组成部分,具有极高的安全风险,因此隧道安全监测是必不可少的。振弦传感器和无线振弦采集仪作为隧道安全监测的两种重要设备,能够有效地监测隧道的振动情况&#…...

c# xml 参数读取的复杂使用
完整使用2 生产厂家里面包含很多规格型号,一个规格型号里面包含很多出厂序列号,点击下一步如果检测到填充的和保存的不一样 就新增一条(如检测到生产厂家相同,但是规格型号不同,就新增一组规格型号)。 界面一:新增界面 界面2 删除界面 界面一:新增界面 load 其中…...

在Mac中使用 brew services start redis 命令启动、停止Redis服务报错
一、问题现象 启动Redis服务命令: brew services start redis异常信息如下: Error: uninitialized constant Homebrew::Service::System /opt/homebrew/Library/Homebrew/macos_version.rb:150:in const_missing /opt/homebrew/Library/Taps/homebrew…...

iapp源码-----比较经典
2.0底部菜单导航栏.rar: https://url18.ctfile.com/f/7715018-958700751-6096bd?p6511 (访问密码: 6511) 2.0涟漪_拖动条控制音乐播放.rar: https://url18.ctfile.com/f/7715018-958700754-4cec13?p6511 (访问密码: 6511) 2.0手电筒.rar: https://url18.ctfile.com/f/7715018…...

为什么手机会莫名多出许多软件?
许多手机用户都曾遭遇过这样的问题,他们在使用手机的过程中,突然发现手机屏幕上出现了一些未知的软件。这些软件并非他们主动下载的,但它们却显现在屏幕上。这些软件从何而来? 其实,这些软件往往是在浏览网页、阅读小…...

测试自动化的边缘:DevTestOps 和 DevSecOps
什么是 DevOps? DevOps 允许企业通过自动化基础设施、工作流程和持续测量应用程序的性能来提高开发人员和运营团队之间的协作和生产力。通过 DevOps,开发人员可以以小块的形式编写代码,以便在几个小时内集成、测试、监控和部署代码ÿ…...
fatal:Could not read from remote repository解决方法
Linux服务器如何连接GitHub? 生成SSH密钥 ssh-keygen -C “邮箱” -t rsa 存放位置一般是/root/.ssh/id_rsa 登录个人github,添加客户端生成的公钥 打开Settings,点击SSH and GPG keys,点击New SSH Key。Key中粘贴id_rsa.pub…...

数学基础
线性代数 关键词:线性方程组、矩阵、增广矩阵(系数矩阵、常数项矩阵)、阶梯型矩阵、行最简矩阵、最简形矩阵、向量系统、向量加法、向量空间、基本单位向量、线性相关、线性无关、Span张成空间、 向量乘法(点积、内积、外积、叉积…...

【Python】Python语言基础(上)
第一章 前言 1. Python简介 Python语言并不是新的语言,它早于HTTP 1.0协议5年,早于Java语言 4年。 Python是由荷兰人Guido van Rossum(吉多范罗苏姆)于1989年圣诞节期间在阿姆斯特丹休假时为了打发无聊的假期而编写的一个脚本…...

C#设计模式六大原则之依赖倒置原则
C#设计模式六大原则是单一职责原则、里氏替换原则、依赖倒置原则、接口隔离原则、迪米特法则、开闭原则。它们不是要我们刻板的遵守,而是根据实际需要灵活运用。只要对它们的遵守程度在一个合理的范围内,努为做到一个良好的设计。以下介绍C#依赖倒置原则…...
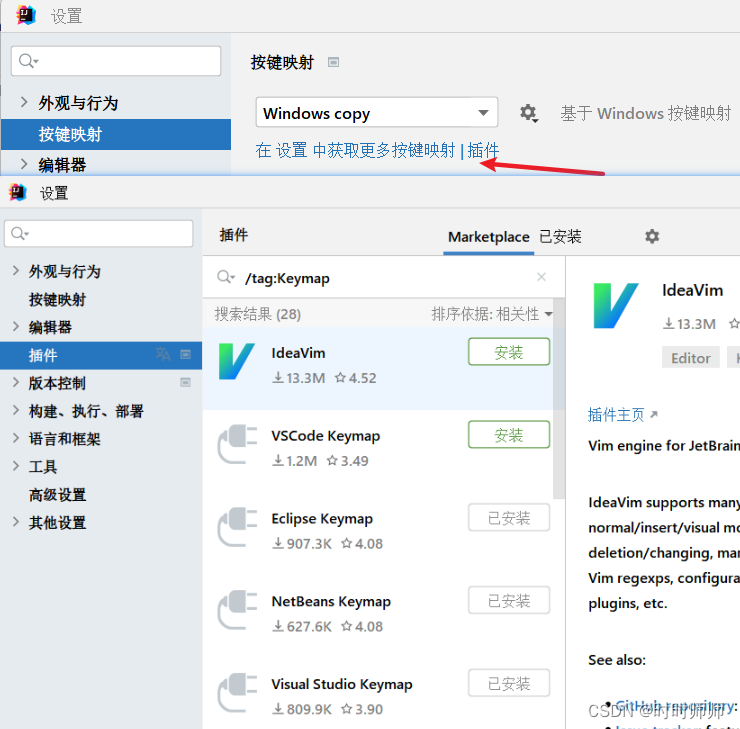
IDEA的使用(二)快捷键 (IntelliJ IDEA 2022.1.3版本)
1. IDEA中的常用快捷键 1.1 通用型快捷键 1.2 提高编写速度 ctrl shift ↑或↓ 只能在方法里面移动代码。 alt shift ↑或↓ 可以向方法外移动代码。 设置过自动导包,所以不用批量导包啦。 1.3 类结构、查找和查看源码 1.4 查找、替换和关闭 1.5 调整格式 1.6 De…...

微信小程序个人账号申请和配置详细教程
一、注册小程序管理账号 1、注册方法 在微信公众平台官网首页(mp.weixin.qq.com),点击右上角的“立即注册”按钮。 2、选择注册的账号类型 选择“小程序”,点击“查看类型区别”可查看不同类型账号的区别和优势。 3、填写邮箱和…...

opencv定位图片中的图案?
import cv2 as cv2def find_positions(image_path, small_image_path):# 读取大图和小图large_image cv2.imread(image_path)small_image cv2.imread(small_image_path)# 小图规格small_image_h, small_image_w small_image.shape[:2]# 对比大图与小图# 匹配模板res cv2.ma…...

高防CDN:网络安全的不可或缺之选
在当今数字化时代,网络攻击已经成为互联网上的一种不可避免的风险。为了应对不断升级的网络威胁,许多企业和组织正在采用高防御CDN(Content Delivery Network)技术,以确保他们的在线资产得到保护,用户体验得…...

flutter 常用组件:文本、图片和按钮
文章目录 文本控件富文本控件图片本地图片网络图片按钮文本控件 ##一’码’当先 Text(这是一段文本这是一段文本这是一段文本这是一段文本这是一段文本这是一段文本这是一段文本这是一段文本,textAlign:TextAlign.center,style: TextStyle(fontWeight: FontWeight.bold, font…...

BI工具:让数据分析井然有序一望而知
BI(Business Intelligence)工具是一类专门用于数据分析和决策支持的软件工具。 它们能够将企业内部和外部的数据进行整合、处理和可视化,帮助用户从海量数据中获取有价值的见解和洞察,并以直观、易懂的方式展示给决策者和相关人员…...
2024级199管理类联考之逻辑核心基础
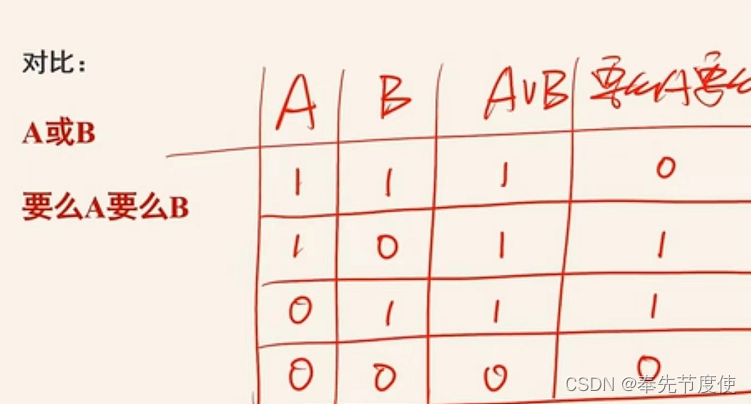
且与或 含义 A且B(A^B):同时存在 常见形式 A并且B既A又B不但A而且B虽然A但是BA或B:二者至少有一个成立(即A且非B,非A且B,A且B) 否定形式 且的否定 A且B否定形式:非(A^B) 非A 或 非B非A且非B否定形式:非(非A^非B) A 或 B非A且B否定形式:…...
)
第二次课,文件校验(预习)
hash 计算接口 Crypto API (证书,对称加密,非对称加密,编码和解码) CryptAcquireContext CryptCreateHash CryptReleaseContext CryptHashData CryptDestroyHash CryptGetHashParam 注册表操作接口 RegEnumKeyEx RegE…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
