C++算法:图中的最短环
题目
现有一个含 n 个顶点的 双向 图,每个顶点按从 0 到 n - 1 标记。图中的边由二维整数数组 edges 表示,其中 edges[i] = [ui, vi] 表示顶点 ui 和 vi 之间存在一条边。每对顶点最多通过一条边连接,并且不存在与自身相连的顶点。
返回图中 最短 环的长度。如果不存在环,则返回 -1 。
环 是指以同一节点开始和结束,并且路径中的每条边仅使用一次。
2 <= n <= 1000
1 <= edges.length <= 1000
edges[i].length == 2
0 <= ui, vi < n
ui != vi
不存在重复的边
分析

返回还是真环
利用BFS求到A的最短距离,B和C到A的距离都为1,处理BC是发现B和C都已经和A连通,说明存在环。注意:求EFG到点D的距离,处理完DE ED EF FE FG后,处理GF,发现F和G都和D连通。判断是返回,还是真环有两种思路:
一,记录已经使用的双向边,枚举新边的时候,忽略。此方案容易理解。
二,记录各点的最短距离的前一点。此方案性能。
各点都要BFS
如果以H为源点,则最短的环长4。以k为源点,最短的环是3。
多个连通区域
由于所有点都会作为起点,所以所有点都会处理。和起点不连通的点不会重复处理。
不会遗漏任意环
某个包括x的奇数长度的环,假定其长度为len2+1,环上有两个点距离x为len,假定先处理的为x1,后处理的为x2。处理x1->x2是发现此环。假定此环长为偶数,假定其长度为len2+2。环上有两个点距离x为len,假定先处理的为x1,后处理的为x2。距离x为len+1的点为x3,则处理x2->x3时,发现此环。
不会误判环
发现cur和next都和源点连通,那说明next在cur之前已经处理,也就是vDis[next] <= vDis[cur]。vDis[next]不会比v[cur]小2,否则源点->next->cur更短。也就是vDis[next]和vDis[cur]相等或少1。源点到next的最短路径,不会包括cur,否则vDis[next]大于v[cur]。两者相等的情况,cur的最短路径不会包括next。少1的情况,如果cur的最短路径包括next,则最后一条边是next->cur。
方案一代码
class Solution {
public:
int findShortestCycle(int n, vector<vector>& edges) {
CNeiBo2 neiBo(n, edges, false);
for (int i = 0; i < n; i++)
{
Do(neiBo.m_vNeiB, i);
}
return (INT_MAX == m_iMinCycle) ? -1 : m_iMinCycle;
}
void Do(const vector<vector>& vNeiB, int src)
{
int n = vNeiB.size();
vector<unordered_set> setHas(n);
vector vDis(n, -1);
queue q;
vDis[src] = 0;
q.emplace(src);
while (q.size())
{
const auto cur = q.front();
q.pop();
for (const auto& next : vNeiB[cur])
{
if (setHas[next].count(cur))
{
continue;
}
setHas[cur].emplace(next);
if (-1 != vDis[next])
{
m_iMinCycle = min(m_iMinCycle, vDis[cur] + vDis[next] + 1);
continue;
}
vDis[next] = vDis[cur] + 1;
q.emplace(next);
}
}
}
int m_iMinCycle = INT_MAX;
};
方案二代码
class Solution {
public:int findShortestCycle(int n, vector<vector<int>>& edges) {CNeiBo2 neiBo(n, edges, false);for (int i = 0; i < n; i++){Do(neiBo.m_vNeiB, i);}return (INT_MAX == m_iMinCycle) ? -1 : m_iMinCycle;}void Do(const vector<vector<int>>& vNeiB, int src){int n = vNeiB.size();vector<int> vDis(n, -1), vPre(n,-1);queue<int> q;vDis[src] = 0;vPre[src] = -1;q.emplace(src);while (q.size()){const auto cur = q.front();q.pop();for (const auto& next : vNeiB[cur]){ if (-1 != vDis[next]){if (vPre[cur] != next){m_iMinCycle = min(m_iMinCycle, vDis[cur] + vDis[next] + 1);}continue;}vDis[next] = vDis[cur] + 1;vPre[next] = cur;q.emplace(next);}} }int m_iMinCycle = INT_MAX;
};
方案三
方案一和方案二时间复杂度都是O(n^2),方案一比方案二慢。方案三相比方案一,稍稍提速。
void Do(const vector<vector>& vNeiB, int src)
{
int n = vNeiB.size();
vector<int> vDis(n, -1);
queue<int> q;
vDis[src] = 0;
q.emplace(src);
while (q.size())
{const auto cur = q.front();q.pop();for (const auto& next : vNeiB[cur]){if (m_vHasDo[next][cur]){continue;}m_vHasDo[cur][next] = 1;if (-1 != vDis[next]){m_iMinCycle = min(m_iMinCycle, vDis[cur] + vDis[next] + 1);continue;}vDis[next] = vDis[cur] + 1;q.emplace(next);}
}
}
2023年4月版本
class Solution {
public:
int findShortestCycle(int n, vector<vector>& edges) {
m_iN = n;
m_vNeiB.resize(n);
for (const auto&v : edges)
{
m_vNeiB[v[0]].emplace_back(v[1]);
m_vNeiB[v[1]].emplace_back(v[0]);
}
for (int i = 0; i < n; i++){bfs(i);}return (INT_MAX == m_iRet) ? -1 : m_iRet;
}
void bfs(int iRoot)
{std::vector<int> vDis(m_iN, -1);vDis[iRoot] = 0;std::queue<pair<int,int>> que;que.emplace(iRoot, -1);//当前节点,父节点while (que.size()){const int iPre = que.front().first;const int iPrePre = que.front().second;que.pop();for (const auto& next : m_vNeiB[iPre]){if (-1 == vDis[next]){vDis[next] = vDis[iPre] + 1;que.emplace(next, iPre);}else{if (next == iPrePre){continue;}m_iRet = min(m_iRet, vDis[iPre] + 1 + vDis[next]);}}}
}
vector<std::vector<int>> m_vNeiB;int m_iN;
int m_iRet = INT_MAX;
};
其它
视频课程
如果你觉得复杂,想从简单的算法开始,可以学习我的视频课程。
https://edu.csdn.net/course/detail/38771
我的其它课程
https://edu.csdn.net/lecturer/6176
测试环境
win7 VS2019 C++17
相关下载
算法精讲《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
相关文章:

C++算法:图中的最短环
题目 现有一个含 n 个顶点的 双向 图,每个顶点按从 0 到 n - 1 标记。图中的边由二维整数数组 edges 表示,其中 edges[i] [ui, vi] 表示顶点 ui 和 vi 之间存在一条边。每对顶点最多通过一条边连接,并且不存在与自身相连的顶点。 返回图中 …...

C++学习——类其实也是一种作用域
以下内容源于C语言中文网的学习与整理,非原创,如有侵权请告知删除。 其实也是一种作用域,每个类都会定义它自己的作用域。在类的作用域之外,普通的成员只能通过对象(可以是对象本身,也可以是对象指针或对象…...

Seata入门系列【4】undo_log、global_table、branch_table、lock_table字段及作用详解
1 客户端 1.1 undo_log 在AT模式中,需要在参与全局事务的数据库中,添加一个undo_log表,建表语句如下: SET NAMES utf8mb4; SET FOREIGN_KEY_CHECKS 0;-- ---------------------------- -- Table structure for undo_log -- --…...

虚幻引擎:数据表格的C++常用API
1.将数据表格中的所有数据存到一个数组中 //参数1 // 错误提示 //参数2 // 存储的数组 TArray<FKeyInfoHeader*> array; KeyInfoDT->GetAllRows<FKeyInfoHeader>(TEXT("错误"),array); 2.获取表格中所有的行名称 TArray<FName>array; …...
)
Java日期格式化(DateFormat类和SimpleDateFormat类)
格式化日期表示将日期/时间格式转换为预先定义的日期/时间格式。例如将日期“Fri May 18 15:46:24 CST2016” 格式转换为 “2016-5-18 15:46:24 星期五”的格式。 在 java 中,可以使用 DateFormat 类和 SimpleDateFormat 类来格式化日期,下面详细介绍这两…...
centos 7 lamp owncloud
OwnCloud是一款开源的云存储软件,基于PHP的自建网盘。基本上是私人使用,没有用户注册功能,但是有用户添加功能,你可以无限制地添加用户,OwnCloud支持多个平台(windows,MAC,Android&a…...

屏幕亮度调节保护您的眼睛
官方下载地址: 安果移动 视频演示:屏幕亮度调节-保护您的眼睛_哔哩哔哩_bilibili 嗨,亲爱的用户,你是否有过这样的体验:夜晚安静的时刻,想要在抖音上看看热门的舞蹈、在快手上发现生活的 趣味、或是在哔…...

CentOS Linux下CMake二进制文件安装并使用Visual Studio调试
cmake安装——二进制安装(很简单,推荐!!) 1)下载二进制包。首先就是官网下载二进制安装包(我们是64位系统,就下载对应的包),这里。 例如:在/home/DOWNLOAD目录下执行,即下载二进制…...

ASP.net相关目录,相关配置文件和.后缀名解释
App_Data:用于存储应用程序的数据文件,例如数据库文件或其他本地文件。 App_Start:包含应用程序的启动配置文件,例如路由配置、日志配置等。 Content:存放应用程序的静态资源文件,如 CSS、JavaScript、图…...
一键批量转换,轻松将TS视频转为MP4视频,实现更广泛的播放和分享!
在享受精彩视频内容的同时,有时我们可能会面临一个问题:某些视频格式可能不太适合我们的播放设备或分享平台。特别是TS格式的视频,在一些情况下可能无法直接播放或上传。但是不用担心,因为我们为您提供了一款强大的视频剪辑工具&a…...
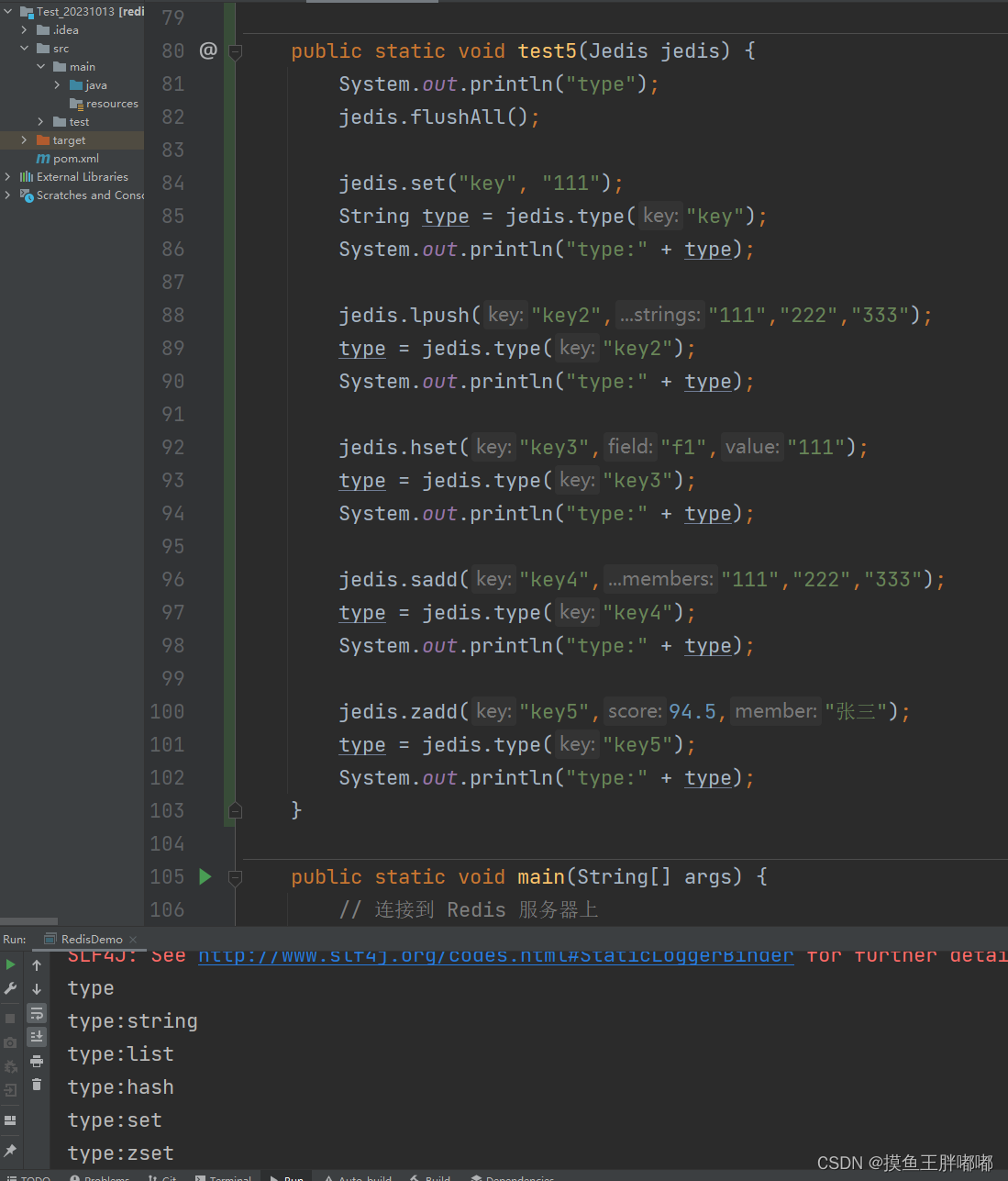
【Redis】使用Java客户端操作Redis
目录 引入jedis依赖连接Redis命令get/setexists/delkeysexpire/ttltype 引入jedis依赖 连接Redis 命令 get/set exists/del keys expire/ttl type...

BSPHP 未授权访问 信息泄露
漏洞描述 BSPHP 存在未授权访问 泄露用户 IP 和 账户名信息 漏洞复现 访问url: 构造payload访问: /admin/index.php?madmin&clog&atable_json&jsonget&soso_ok1&tuser_login_log&page1&limit10&bsphptime16004073…...
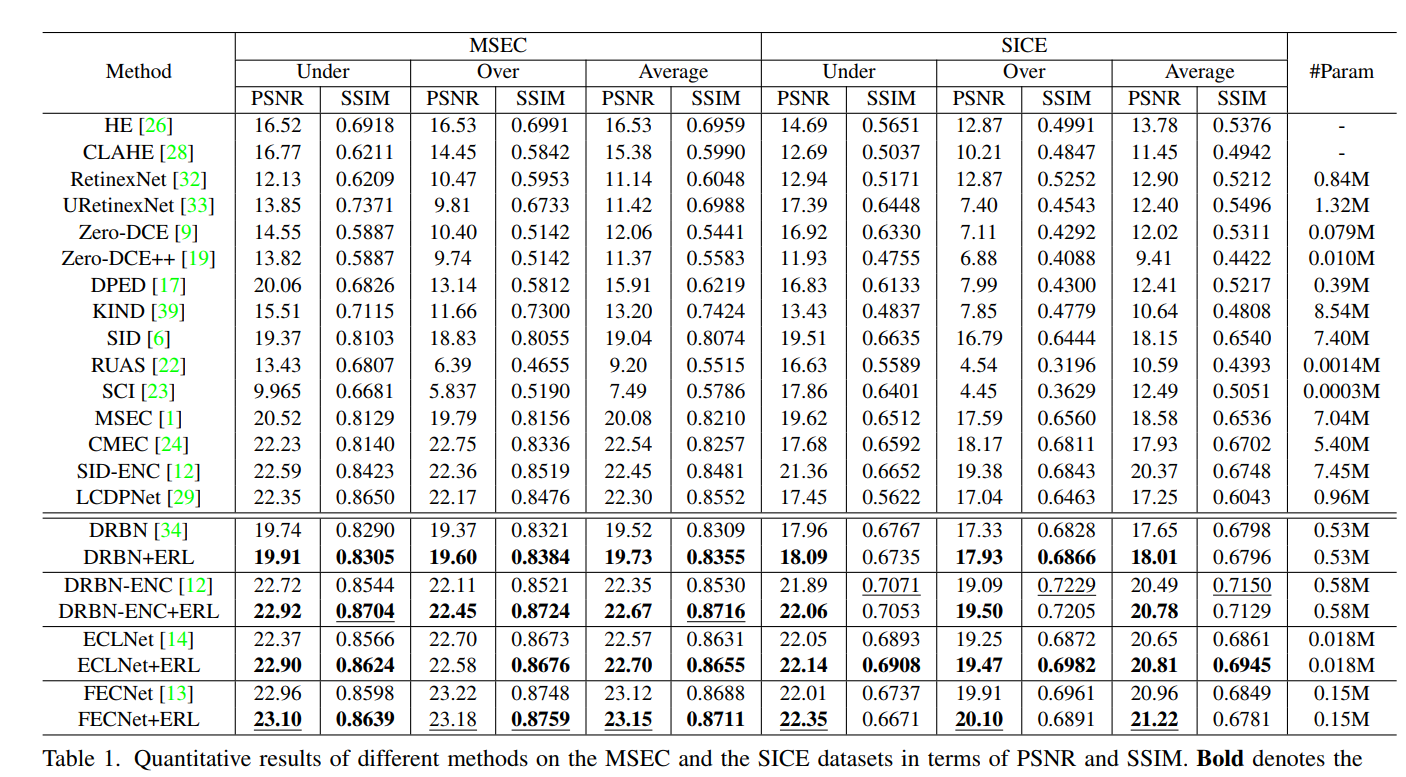
Learning Sample Relationship for Exposure Correction 论文阅读笔记
这是中科大发表在CVPR2023的一篇论文,提出了一个module和一个损失项,能够提高现有exposure correction网络的性能。这已经是最近第三次看到这种论文了,前两篇分别是CVPR2022的ENC(和这篇文章是同一个一作作者)和CVPR20…...

Vue项目 -- 解决Eslint导致的console报错问题
在利用vue-cli3构建的项目中引入eslint进行语法检查时,使用console.log(‘xxx’)时,控制台抛出了Unexpected console statement (no-console) 异常, 例:一使用console就提示报错 解决办法是: 在 .eslintrc.js 文件中…...

uni-app 在已有的数据对象中动态添加更多的数据对象
原数据对象 flowData: {list: [], // 数据值column: 2, // 瀑布列数columnSpace: 2 // 瀑布列宽间距 } 动态添加后的数据对象 flowData: {list: [], // 数据值column: 2, // 瀑布列数columnSpace: 2, // 瀑布列宽间距column_1: [],column_2: [] } 动态添加更多的数据对象的…...

【LeetCode】17. 电话号码的字母组合
1 问题 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 示例 1: 输入:digits “23” 输出&…...
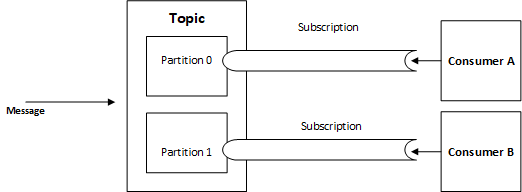
使用 Apache Kafka 进行发布-订阅通信中的微服务
发布-订阅消息系统在任何企业架构中都发挥着重要作用,因为它可以实现可靠的集成,而无需紧密耦合应用程序。在解耦的系统之间共享数据的能力并不是一个容易解决的问题。 考虑一家拥有多个使用不同语言和平台独立构建的应用程序的企业。它需要响应地共享数…...

valarray 包含对象成员的类(cpp14章)
C代码重用 1.公有继承可以实现 2.包含、私有继承、保护继承用于实现has-a关系,即新的类将包含另一个类的对象。 (使用这样类成员:本身是另外一个类对象称为包含 (组合或层次化)。) 3.函数模板、类模…...
)
2023双11笔记本电脑候选名单(截止2023.10.13的价格,双十一活动可能会更便宜一点)
以下是我最近几天查阅抖音,B站,知乎,百度,朋友后候选出来的一些6000-8000的游戏本电脑,标绿的属性是相比之下较为优秀的 附上几个网上的CPU和显卡排行网站 CPU性能排行榜 - CPU天梯图 - 最强CPU2023(较为全面的CPU排行,收录四千多款) 笔记本性能排行榜 - 快科技天梯榜 笔记本CP…...
-客户端负载均衡Ribbon)
Springcloud笔记(4)-客户端负载均衡Ribbon
Ribbon是一个基于HTTP和TCP的客户端负载均衡工具,不需要独立部署,几乎存在于每一个springcloud构建的微服务和基础设施中。 微服务间调用,API网关的请求转发都通过Ribbon实现。 负载均衡 通常所说的负载均衡都是指的服务端负载均衡…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
