区块链（11）：java区块链项目之页面部分实现
addPeer.html
<!DOCTYPE html>
<html>
<head><meta charset="utf-8"> <title>java区块链</title><meta name="viewport" content="width=device-width, initial-scale=1"><link rel="stylesheet" href="http://cdn.static.runoob.com/libs/bootstrap/3.3.7/css/bootstrap.min.css"> <script src="http://cdn.static.runoob.com/libs/jquery/2.1.1/jquery.min.js"></script><script src="http://cdn.static.runoob.com/libs/bootstrap/3.3.7/js/bootstrap.min.js"></script><script>$(function() { $("#mineing").html("点击添加节点").css("color","red");$("#myButton4").click(function(){var params={};var data = $("#data").val();if(data==""){aler相关文章：
区块链（11）：java区块链项目之页面部分实现
addPeer.html <!DOCTYPE html> <html> <head><meta charset="utf-8"> <title>java区块链</title><meta name="viewport" content="width=device-width, initial-scale=1"><link rel="styles…...
RootSIFT---SIFT图像特征的扩展
RootSIFT是论文 Three things everyone should know to improve object retrieval - 2012所提出的 A Comparative Analysis of RootSIFT and SIFT Methods for Drowsy Features Extraction - 2020 当比较直方图时，使用欧氏距离通常比卡方距离或Hellinger核时的性能…...
ChatGPT角色扮演教程，Prompt词分享
使用指南 1、可直复制使用 2、可以前往已经添加好Prompt预设的AI系统测试使用 https://ai.idcyli.comhttps://ai.idcyli.com 雅思写作考官 我希望你假定自己是雅思写作考官，根据雅思评判标准，按我给你的雅思考题和对应答案给我评分，并且按…...
zabbix监控——自定义监控内容
目录 自定义监控项步骤 案例 1、明确需要执行的命令 2、创建 zabbix 的监控项配置文件，用于自定义 key，并重启zabbix-agent2 3、.在服务端验证新建的监控项 4、在 Web 页面创建自定义监控项模板 1）创建模板 2）创建监控项 …...
中断机制-中断协商机制、中断方法
4.1 线程中断机制 4.1.1 从阿里蚂蚁金服面试题讲起 Java.lang.Thread下的三个方法: 4.1.2 什么是中断机制 首先，一个线程不应该由其他线程来强制中断或停止，而是应该由线程自己自行停止，自己来决定自己的命运，所以，…...
three.js入门 —— 实现第一个3D案例
前言： three.js入门，根据文档实现第一个3D案例 效果图： 代码实现： const scene new THREE.Scene();//创建一个长方体几何对象Geometryconst geometry new THREE.BoxGeometry(100, 100, 100);//创建一个网络基础材质的材质对象…...
《动手学深度学习 Pytorch版》 8.4 循环神经网络
8.4.1 无隐状态的神经网络 对于无隐藏装态的神经网络来说，给定一个小批量样本 X ∈ R n d \boldsymbol{X}\in\mathbb{R}^{n\times d} X∈Rnd，则隐藏层的输出 H ∈ R n h \boldsymbol{H}\in\mathbb{R}^{n\times h} H∈Rnh 通过下式计算： …...
什么是物联网阀控水表？
物联网阀控水表是一种新型的水表，结合了物联网技术和传统水表的功能，可以实现对水的计量、控制和管理。随着人们对水资源的日益重视，物联网阀控水表的应用越来越广泛，为水资源的合理利用和管理提供了有效手段。 物联网阀控水表是由…...
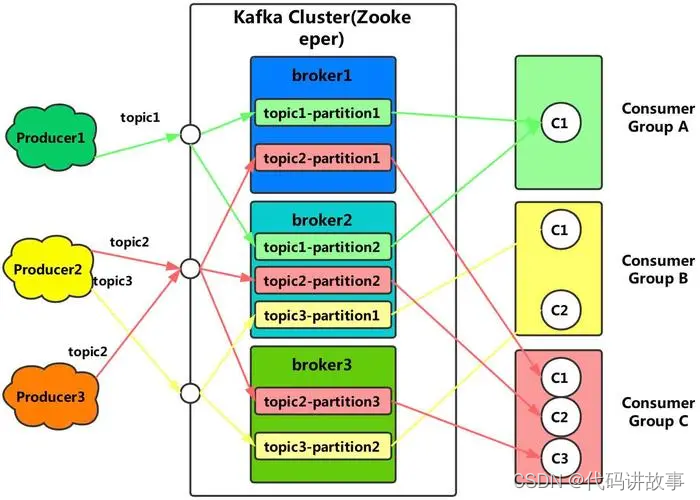
Kafka 开启SASL/SCRAM认证 及 ACL授权（一）认证
Kafka 开启SASL/SCRAM认证 及 ACL授权（一）认证。 kafka安全涉及3部份：传输加密，用户认证与授权，ZK开启ACL（Zookeeper存储了kafka的元数据以及用户信息，默认不开启acl所有用户可改，内网环境机器不对外开放可考虑使用默认不开启ZK ACL）。 官网地址：https://kafka.ap…...
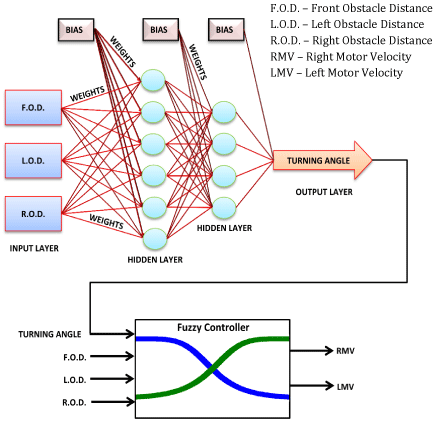
关于智能控制领域中模糊控制算法的概述
智能控制领域中的模糊控制算法是一种基于模糊逻辑的控制策略，它通过对模糊集合的刻画来处理模糊信息，从而获得模糊输出并进行控制。模糊控制算法在实际控制工程中具有良好的应用前景，它不但具有较强的鲁棒性和适应性，而且可以为复…...
剖析伦敦银最新价格走势图
国际金融市场瞬息万变，伦敦银的价格走势会受到诸多因素的影响，比如重要经济数据的公布，国际间的政治博弈，突发的政经大事，都可以令白银价格的走势，在短时间内暴涨暴跌的情况。 要在伦敦银市场实现良好的收益…...
通用人工智能技术（深度学习，大模型，Chatgpt，多模态，强化学习，具身智能）
目录 前言 1.通用人工智能 1.1 生物学分析 1.2具身智能 1.2.1当前的人工智能的局限 1.2.2 具身智能实现的基础 1.2.3 强化学习（决策大模型） 2.结论 往期文章 参考文献 前言 目前的人工智能实质上只是强人工智能，或者说单个领域的通…...
makefile的特性-部分语法记录
1.变量定义 1.1 来实现a1 $(a2)a2 lib.o1.2 : 来实现, 这种不能通过后面的变量来定义a1 : $(a2) b.0a2 : lib.o1.3 来实现a1 b.0a2 a11.4 ? 来实现,这种方式前面如果定义了，后面定义则无效a1 : a.oa1 ? lib.o //结果 a1 a.o 2.文件查找 2.1 VPATH 目录…...
【Java 进阶篇】JavaScript 正则表达式（RegExp）详解
JavaScript 正则表达式，通常简写为 RegExp，是一种强大的文本匹配工具，它允许你通过一种灵活的语法来查找和替换字符串中的文本。正则表达式在编程中用途广泛，不仅限于 JavaScript，在许多编程语言中也都有类似的实现。 …...
51单片机之串口通信例程
51单片机之串口通信例程 简介原理例程 简介 串行通信是指使用一条数据线，将数据一位一位地依次传输，每一位数据占据一个固定的时间长度。在串行通信中，数据可以以字符为单位进行传输，也可以以帧为单位进行传输。 在51单片机中&a…...
Hadoop高可用集群（HA）一键启动脚本
高可用集群启动时，需要分别在每个节点上都执行zkServer.sh start启动zookeeper，这个过程比较麻烦，并且当我们节点增多时，这个过程无疑不增加了我们的工作量，因此我们可以写一个一键启动所有节点zookeeper的脚本 脚本实…...
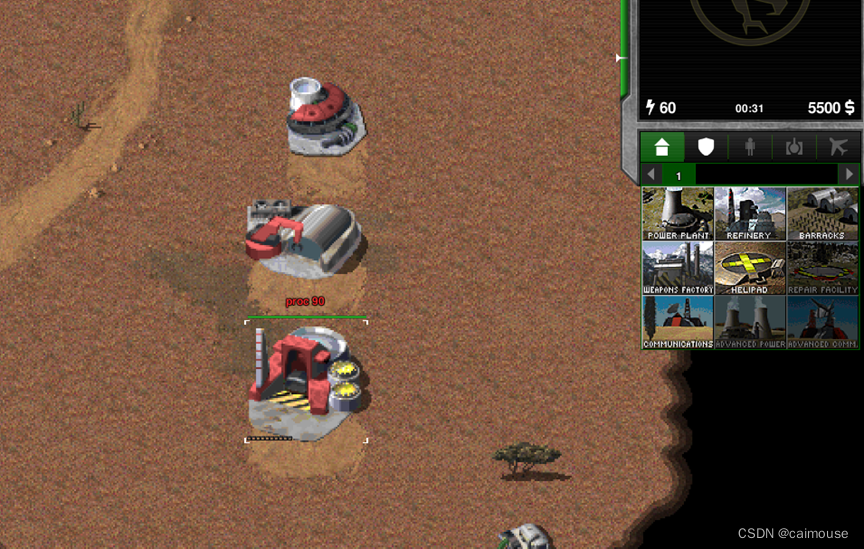
C#开发的OpenRA游戏之金钱系统（1）
C#开发的OpenRA游戏之金钱系统（1） 设计一个游戏，肯定要有一个唯一的资源，用这个资源来管理整个游戏的进度，以及相互争夺的焦点。在OpenRA里，就是使用矿产资源。所以在地图上分布几个矿场，玩家就需要相互争夺矿场，谁开采多谁就更有钱，谁有钱了就可以升级更好的科技，以…...
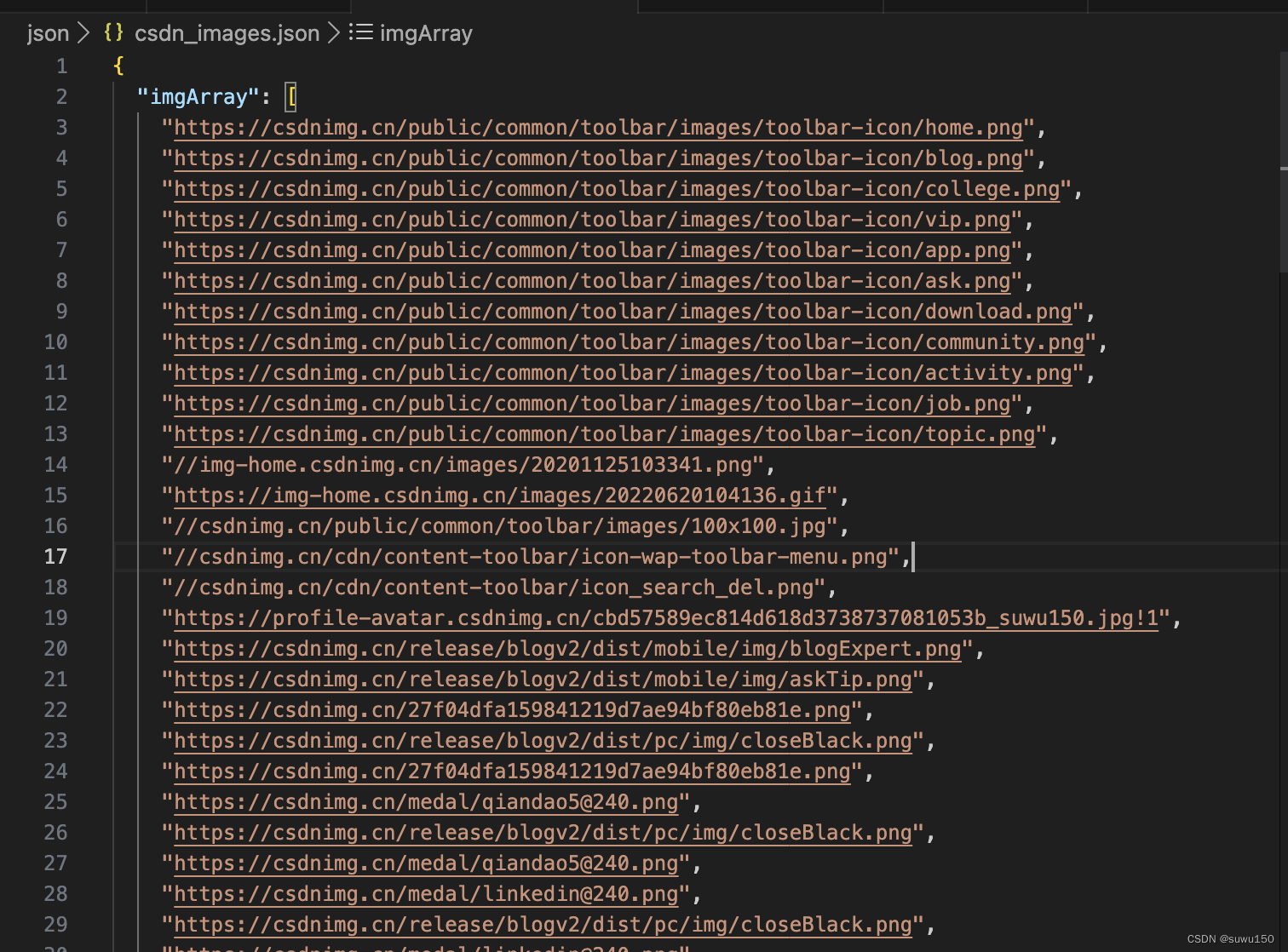
Puppeteer监听网络请求、爬取网页图片（二）
Puppeteer监听网络请求、爬取网页图片（二） Puppeteer监听网络请求、爬取网页图片（二）一、爬取需求二、实现讲解三、效果查看 一、爬取需求 首先打开浏览器，打开指定网站监听网站发出的所有请求，记录请求&a…...
GoLang连接mysql数据库
跟着文档走GORM 指南 | GORM - The fantastic ORM library for Golang, aims to be developer friendly. 1.使用命令拉取 go get -u gorm.io/gorm go get -u gorm.io/driver/sqlite2.开始使用 package mainimport ("fmt""github.com/gin-gonic/gin"&…...
软件工程与计算总结（八）软件设计基础
一.设计思想的发展 1958：软件这个名词第一次在公开刊物上使用~60年代中后期and70年代前中期：结构化编程、逐步求精、自顶向下理念是程序设计主要方法70年代中后期and90年代：结构化设计方法、抽象数据类型、信息隐藏、封装、继承、多态等思想…...
JavaSec-RCE
简介 RCE(Remote Code Execution)，可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景：Groovy代码注入 Groovy是一种基于JVM的动态语言，语法简洁，支持闭包、动态类型和Java互操作性，…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源： http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...
【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1：执行计划绑定问题？尝试：SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库，并对 SQL 进行优化了，添加了强制索引。 UAT 环境已经生效，但 PROD 环境强制索…...
IGP（Interior Gateway Protocol，内部网关协议）
IGP（Interior Gateway Protocol，内部网关协议） 是一种用于在一个自治系统（AS）内部传递路由信息的路由协议，主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...
剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表，若其中包含环，则输出环的入口节点。 若其中不包含环，则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...
【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课，做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程，它的核心机制是 Goroutine 协程、Channel 通道，并基于CSP（Communicating Sequential Processes࿰…...
CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库，而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例，演示如何： 使用 FetchContent 从 GitH…...
C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj，再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）
考察一般的三次多项式，以r为参数： p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]； 此多项式的根为： 尽管看起来这个多项式是特殊的，其实一般的三次多项式都是可以通过线性变换化为这个形式…...
计算机基础知识解析：从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域：无处不在的数字助手 2、 计算机的进化史：从算盘到量子计算 3、计算机的分类：不止 “台式机和笔记本” 4、计算机的组件：硬件与软件的协同 4.1 硬件：五大核心部件 4.2 软件&#…...