【LeetCode第115场双周赛】100029. 和带限制的子多重集合的数目 | 前缀和背包 | 中等
题目内容
原题链接
给定一个长度为 n n n 的数组 n u m s nums nums 和一个区间左右端点 [ l , r ] [l,r] [l,r] 。
返回 n u m s nums nums 中子多重集合的和在闭区间 [ l , r ] [l, r] [l,r] 之间的 子多重集合的数目 。
子多重集合 指的是从数组中选出一些元素构成的 无序 集合,每个元素 x x x 出现的次数可以是 0 , 1 , . . . , o c c [ x ] 0, 1, ..., occ[x] 0,1,...,occ[x] 次,其中 o c c [ x ] occ[x] occ[x] 是元素 x x x 在数组中的出现次数。
注意:
- 如果两个子多重集合中的元素排序后一模一样,那么它们两个是相同的子多重集合 。
- 空集合的和是 0 。
数据范围
- 1 ≤ n ≤ 2 ⋅ 1 0 4 1\leq n\leq 2\cdot 10^4 1≤n≤2⋅104
- 0 ≤ n u m s [ i ] ≤ 2 ⋅ 1 0 4 , s u m ( n u m s ) ≤ 2 ⋅ 1 0 4 0\leq nums[i]\leq 2\cdot 10^4, sum(nums)\leq 2\cdot 10^4 0≤nums[i]≤2⋅104,sum(nums)≤2⋅104
- 0 ≤ l ≤ r ≤ 2 ⋅ 1 0 4 0\leq l\leq r\leq 2\cdot 10^4 0≤l≤r≤2⋅104
题解
本题从数据范围出发。
考虑 n u m s nums nums 总和不超过 20000 20000 20000 ,那么 n u m s nums nums 中不同的数有多少个呢?
考虑最小的情况下有 x x x 种数,每种数一个,那么总和为: x × ( x + 1 ) 2 \frac{x\times (x+1)}{2} 2x×(x+1)
当 x = 200 x=200 x=200 时, x × ( x + 1 ) 2 = 20100 > 20000 \frac{x\times (x+1)}{2}=20100>20000 2x×(x+1)=20100>20000 ,故至多有 199 199 199 个不同的数。
那么问题转换为一个分组背包问题,值为 v v v 的数的个数有 c c c 个,那么可以选择这个数 [ 0 , v ] [0,v] [0,v] 次,这样可以转换成 01 01 01 背包,最多有 O ( n ) O(n) O(n) 个物品。
这样时间复杂度为: O ( n ∑ n u m s ) O(n\sum nums) O(n∑nums) , 4 e 8 4e8 4e8 不能通过。
考虑从定义出发:
d p [ i ] [ j ] dp[i][j] dp[i][j] 表示前 i i i 种物品,容量使用为 j j j 的方案数。
那么 d p [ i ] [ j ] dp[i][j] dp[i][j] 的状态转移方程是什么呢?
d p [ i ] [ j ] = ∑ k d p [ i − 1 ] [ k ] dp[i][j]=\sum\limits_{k} dp[i-1][k] dp[i][j]=k∑dp[i−1][k] ,满足 0 ≤ j − k ≤ c n t [ i ] × v a l [ i ] 0\leq j-k\leq cnt[i]\times val[i] 0≤j−k≤cnt[i]×val[i]
其中 c n t [ i ] cnt[i] cnt[i] 表示第 i i i 个数的数量, v a l [ i ] val[i] val[i] 表示第 i i i 个数的值。
那么就是要求一个区间和了。
麻烦在于如果二维转移,时间复杂度还是 O ( n ∑ n u m s ) O(n\sum nums) O(n∑nums) 。
这里具体的实现是,先用完全背包计算前缀和,然后最多考虑每个数的次数 c n t [ i ] cnt[i] cnt[i] 次。
def func():dp = [0] * (r + 1)dp[0] = 1nums_cnt// 枚举每个数及其次数for v, c in nums_cnt;for i in range(x, r + 1):dp[i] += dp[i - 1]// 这样 dp[i] 就是考虑有 0 个,1 个,... i/v 个数 v 的集合// 做完了前缀和// 但是需要注意的是,数的数量只有 c 个// 所以我们还需要多的部分for i in range(r + 1, (c + 1) * v - 1, -1):// dp[i] 只能由 dp[i], dp[i-v], dp[i-2v], ..., dp[i-cv] // 转移而来,所以对于 dp[i-(c+1)*v]存储的是 i-(c+1)*v 的前缀和,// 其并不能转移到 dp[i] ,删去即可dp[i] -= dp[i-(c + 1) * v]// 最后考虑 0 选择即可,有 zero + 1 种选法return (nums_cnt[0] + 1) * sum(dp[l:r+1])
时间复杂度: O ( 200 ∑ n u m s ) O(200\sum nums) O(200∑nums)
代码
class Solution {
public:int countSubMultisets(vector<int>& nums, int l, int r) {const int MAX = 20010;const int MOD = 1e9 + 7;vector<int> dp(r + 1);dp[0] = 1;vector<int> cnt(MAX);vector<int> vec;int zero = 0;for (int u: nums) {if (u == 0) {zero += 1;continue;}cnt[u] += 1;if (cnt[u] == 1) vec.push_back(u);}for (int u: vec) {for (int i = u; i <= r; ++i) {dp[i] += dp[i - u];if (dp[i] >= MOD) dp[i] -= MOD;}int l = (cnt[u] + 1) * u;for (int i = r; i >= l; --i) {dp[i] -= dp[i - l];if (dp[i] < 0) dp[i] += MOD;}}int ans = 0;for (int i = l; i <= r; ++i) {ans += dp[i];if (ans >= MOD) ans -= MOD;}ans = 1ll * ans * (zero + 1) % MOD;return ans;}
};
相关文章:

【LeetCode第115场双周赛】100029. 和带限制的子多重集合的数目 | 前缀和背包 | 中等
题目内容 原题链接 给定一个长度为 n n n 的数组 n u m s nums nums 和一个区间左右端点 [ l , r ] [l,r] [l,r] 。 返回 n u m s nums nums 中子多重集合的和在闭区间 [ l , r ] [l, r] [l,r] 之间的 子多重集合的数目 。 子多重集合 指的是从数组中选出一些元素构成的 …...

ArcGIS笔记5_生成栅格文件时保存报错怎么办
本文目录 前言Step 1 直接保存到指定文件夹会报错Step 2 先保存到默认位置再数据导出到指定文件夹 前言 有时生成栅格文件时,保存在自定义指定的文件夹内会提示出错,而保存到默认位置则没有问题。因此可以通过先保存到默认位置,再数据导出到…...

YOLO目标检测——跌倒摔倒数据集【含对应voc、coco和yolo三种格式标签】
实际项目应用:公共安全监控、智能家居、工业安全等活动区域无监管情况下的人员摔倒事故数据集说明:YOLO目标检测数据集,真实场景的高质量图片数据,数据场景丰富。使用lableimg标注软件标注,标注框质量高,含…...
uniapp小程序实现绘制内容,生成海报并保存截图(Painter和Canvas两种方式举例)
一、Painter方法 Painter插件传送门 1.下载资源包 2.将资源包的如下部分 3.使用页面引入组件 ui样式 <paintercustomStyle=margin-left: 40rpx; height: 1000rpx;palette="{{palette}}"bind:imgOK="onImgOK"/>data 中数据(绘制内容,替换区域) pai…...

HTTPS双向认证及密钥总结
公钥私钥: 1)公钥加密,私钥解密:加解密 为什么不能私钥加密公钥解密? 私钥加密后,公钥是公开的都能解密,没有意义。 2)私钥签名,公钥验签:属于身份验证,防串改&#x…...
Mybatis用Byte[]存图片,前端显示图片
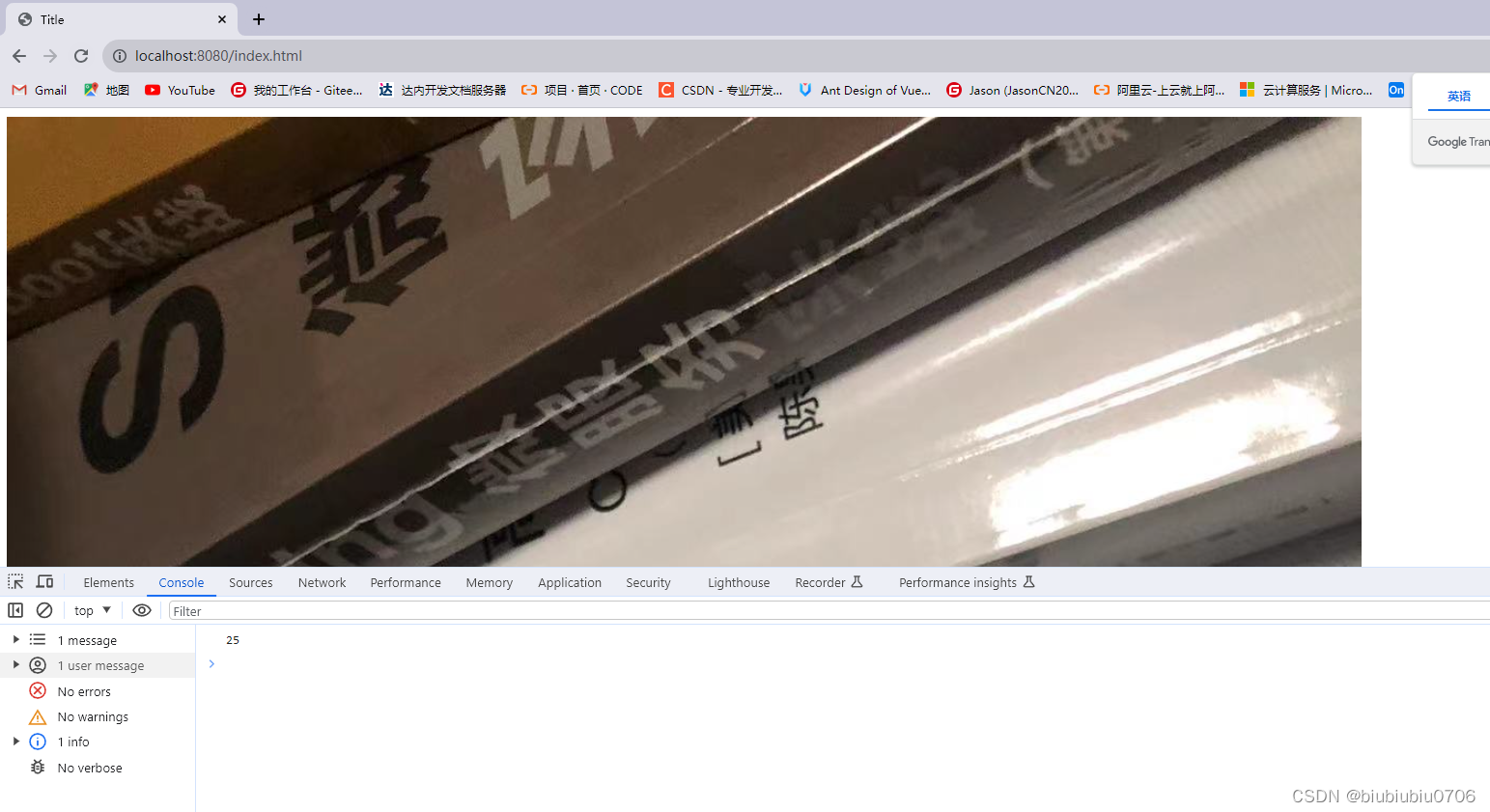
前端页面 static下 也就是说byte[] 转成JSON字符串后,和用BASE64编码后是一摸一样的,那么SpringBoot会自动将实体类转JSON字符串,也就是说根本不需要Base64编码 注意:两个值并非一摸一样,一个多了个双引号 byte[]的值前后有个双引号 有一点点区别 一个有双引号,一个没有…...

MacBook/MacOS如何更新到指定的版本
背景 现在是A版本,想要更新到B,而目前能最新更新到C。 是可以做到的,不一定更新就得更新到最新的。 只要下载好B之后更新即可。 方法 思路是下载好目标的版本后更新,这里可以下载: https://support.apple.com/zh-…...

使用VScode进行C++开发
需要的两个文件 .vscode 目录下 tasks.json {"tasks": [{"type": "cppbuild","label": "C/C: g.exe 生成活动文件","command": "C:/MinGW/bin/g.exe","args": ["-fdiagnostics-color…...

Android Studio的笔记--HttpsURLConnection使用POST请求
HttpsURLConnection使用POST请求 https post请求加返回MainActivity.javaAndroidMainfest.xmlactivity_main.xmllog https post请求加返回 MainActivity.java 用HttpsURLConnection POST方法进行需注意: 1、Android 9及以上版本需要设置这个,否则会有警…...

win redis 配置自启动服务
配置自启动 redis-server --service-install redis.windows-service.conf --loglevel verbose redis.windows-service.conf 配置 Logs 文件夹...

走进Spark
什么是Spark 是一个基于内存的,用于大规模数据处理(离线计算、实时计算、快速查询(交互式查询))的统一分析引擎,因为是基于内存的所以可以更快的完成任务 离线计算:离线计算一般存储在HDFS中使用MapReduce或…...
“小程序:改变电商行业的新趋势“
目录 引言1. 小程序的简介1.1 什么是小程序?1.2 小程序的优势 2. 小程序之电商演示1.注册微信小程序2.安装开发工具3.创建项目 3. 小程序之入门案例总结 引言 随着移动互联网的迅猛发展,小程序作为一种全新的应用形态,正在逐渐改变着传统电商…...
创建图案填充)
Python与CAD系列基础篇(五)创建图案填充
目录 0 简述1 win32com2 ezdxf0 简述 本篇详细介绍使用①pyautocadpyautocad本质是调用接口连接autocad,由于此处未找到正确的填充函数,通过win32com库找到相应填充函数,测试发现更为好用,因此后续将用win32com代替pyautocad连接AutoCAD进行处理 ②通过ezdxf处理dxf格式文…...

终端仿真软件连接交换机调试步骤
背景: 通过一台电脑,连接交换机的console口进行命令行调试; 需要用到终端仿真软件以图形界面显示交换机的命令; 本文以华为交换机和华为提供的终端仿真软件IPOP V4.02为例,其他仿真软件应该类似,可模仿。…...

redis基本数据类型
一) 字符串(String) String是redis最基本的类型,value最大是512M,String类型是二进制安全的,可以包含任何数据,如jpg图片或者序列化的对象 1 使用场景 1) 缓存:redis作为缓存层,mysql做持久化层࿰…...

C++笔记之std::async的用法
C笔记之std::async的用法 code review! 文章目录 C笔记之std::async的用法1.概念2.C 异步任务的使用示例 - 使用 std::async 和 std::future3. std::launch::async 和 std::launch::deferred4.如果需要真正的异步,请指定std::launch::async 1.概念 std::async 是 …...

OpenCV4(C++)—— 图像连通域的详细分析
文章目录 前言一、connectedComponents函数二、connectedComponentsWithStats函数 前言 图像连通域,其实就是图像分割的一种方法。它通过检测像素之间的连接关系和相似性来划分图像中的区域,以便进行后续处理。图像邻域和图像邻域分析就不介绍了&#x…...

Rule-Engine-Starter V1.0.0
一个轻量级的规则引擎、搜索引擎,让条件匹配简单、优雅。 GIT地址 https://gitcode.cosmoplat.com/15011240224/rule-engine-starter 介绍 Rule-Engine-Starter 是一个轻量级规则引擎,V1.0.0主要解决条件匹配问题。比如飞书文档,每个文档都…...
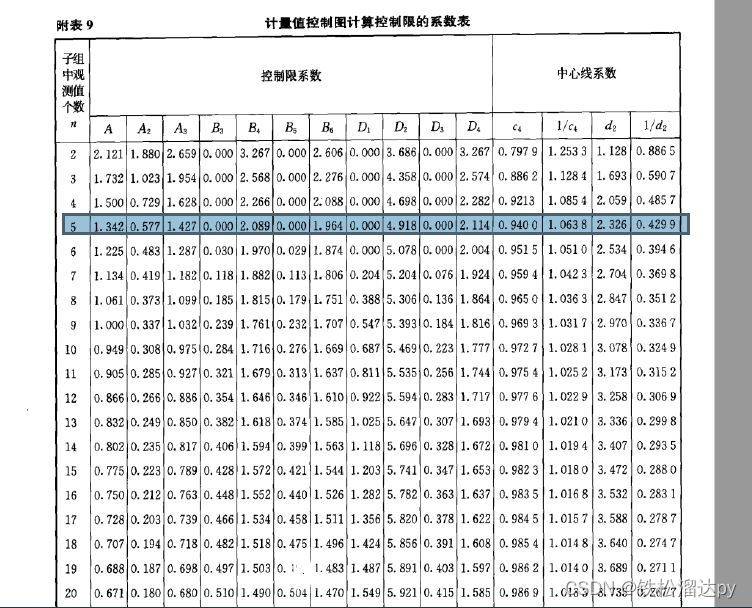
绘制X-Bar-S和X-Bar-R图,监测过程,计算CPK过程能力指数
X-Bar-S图和X-Bar-R图是统计质量控制中常用的两种控制图,用于监测过程的稳定性和一致性。它们的主要区别在于如何计算和呈现数据的变化以及所关注的问题类型。 X-Bar-S图(平均值与标准偏差图): X-Bar代表样本均值,S代表…...

【每日一句】只出现一次的数
文章目录 Tag题目来源题目解读解题思路方法一:位运算 其他语言Cpython3 写在最后 Tag 【位运算-异或和】【数组】【2023-10-14】 题目来源 136. 只出现一次的数字 题目解读 给你一个数组,找出数组中只出现一次的元素。题目保证仅有一个元素出现一次&a…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
