“小程序:改变电商行业的新趋势“
目录
- 引言
- 1. 小程序的简介
- 1.1 什么是小程序?
- 1.2 小程序的优势
- 2. 小程序之电商演示
- 1.注册微信小程序
- 2.安装开发工具
- 3.创建项目
- 3. 小程序之入门案例
- 总结

引言
随着移动互联网的迅猛发展,小程序作为一种全新的应用形态,正在逐渐改变着传统电商行业的格局。本篇博客将从小程序的简介、电商演示以及入门案例三个大目录进行探讨,带您深入了解小程序在电商领域的应用与前景。
1. 小程序的简介
1.1 什么是小程序?
小程序是一种无需下载安装即可使用的应用程序,通过微信等平台直接打开使用,具有轻量化、便捷性和跨平台特点。
1.2 小程序的优势
- 无需下载安装,便于用户快速使用;
- 资源占用少,节省手机存储空间;
- 用户黏性高,留存率较传统应用更高;
- 可与微信生态系统相结合,拓展用户群体;
- 提供丰富的功能组件和API,支持多种业务场景。
2. 小程序之电商演示
1.注册微信小程序
注册链接
https://mp.weixin.qq.com/wxopen/waregister?action=step1
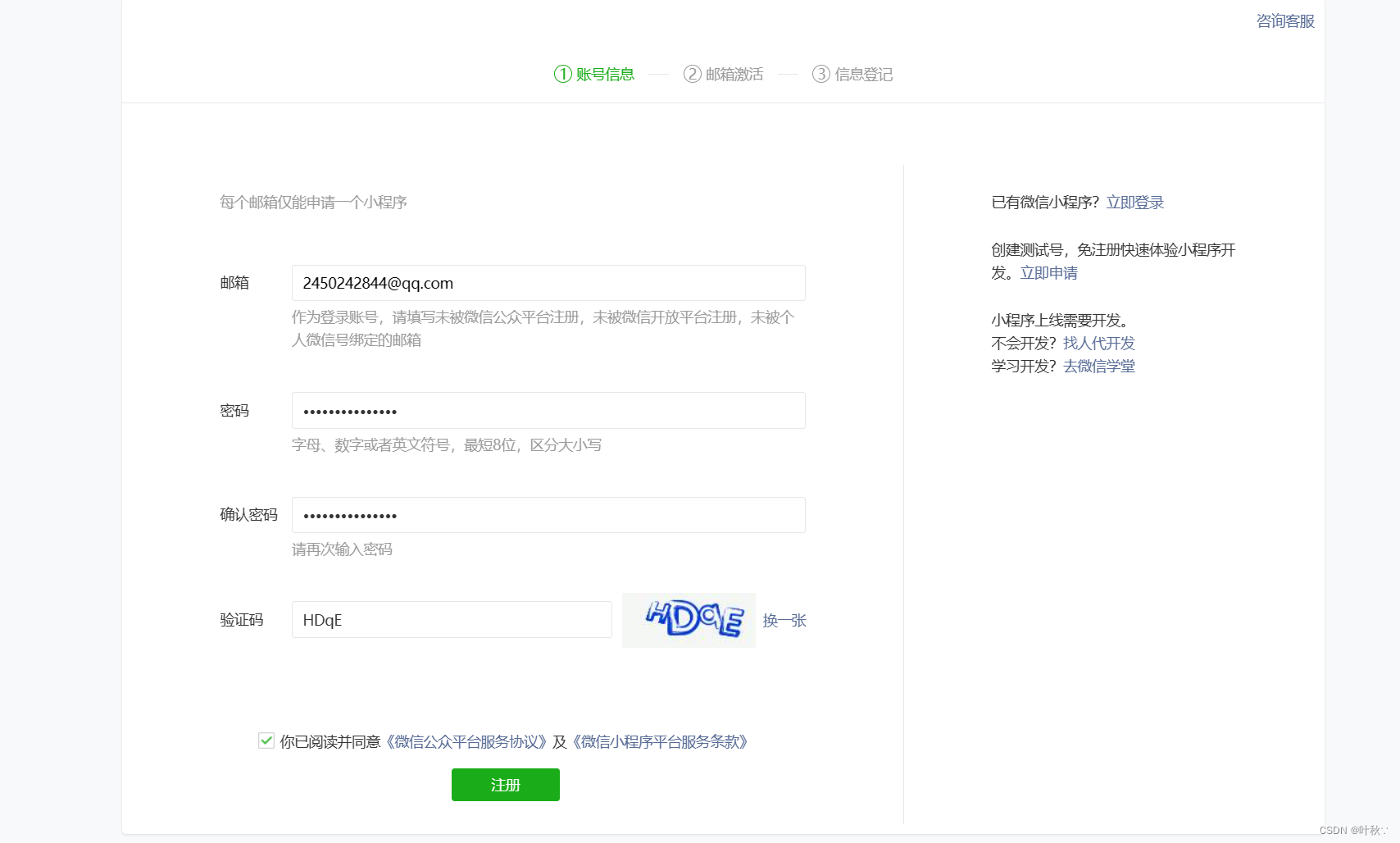
2.安装开发工具
安装链接
https://developers.weixin.qq.com/miniprogram/dev/devtools/download.html
3.创建项目

效果
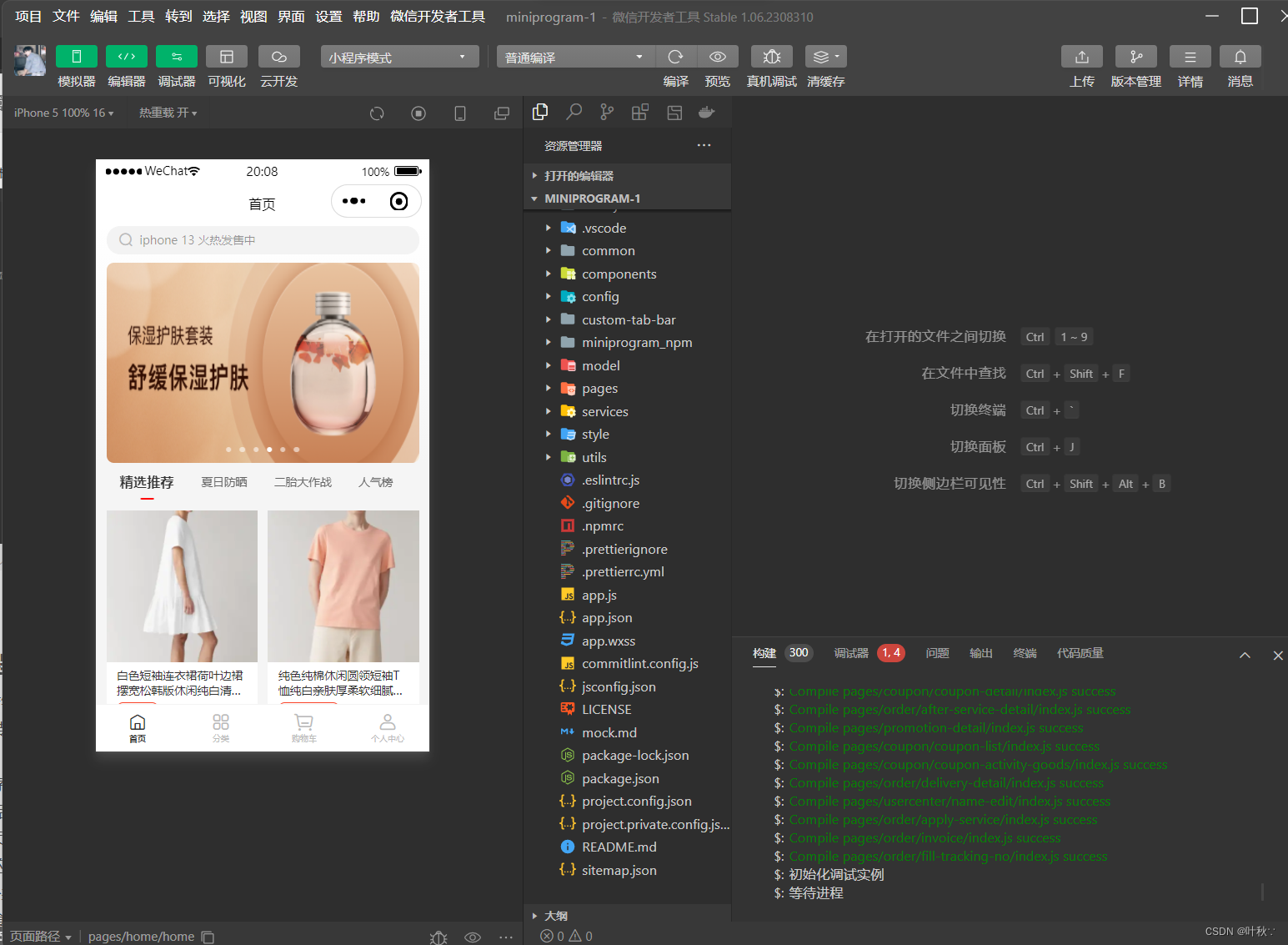
3. 小程序之入门案例
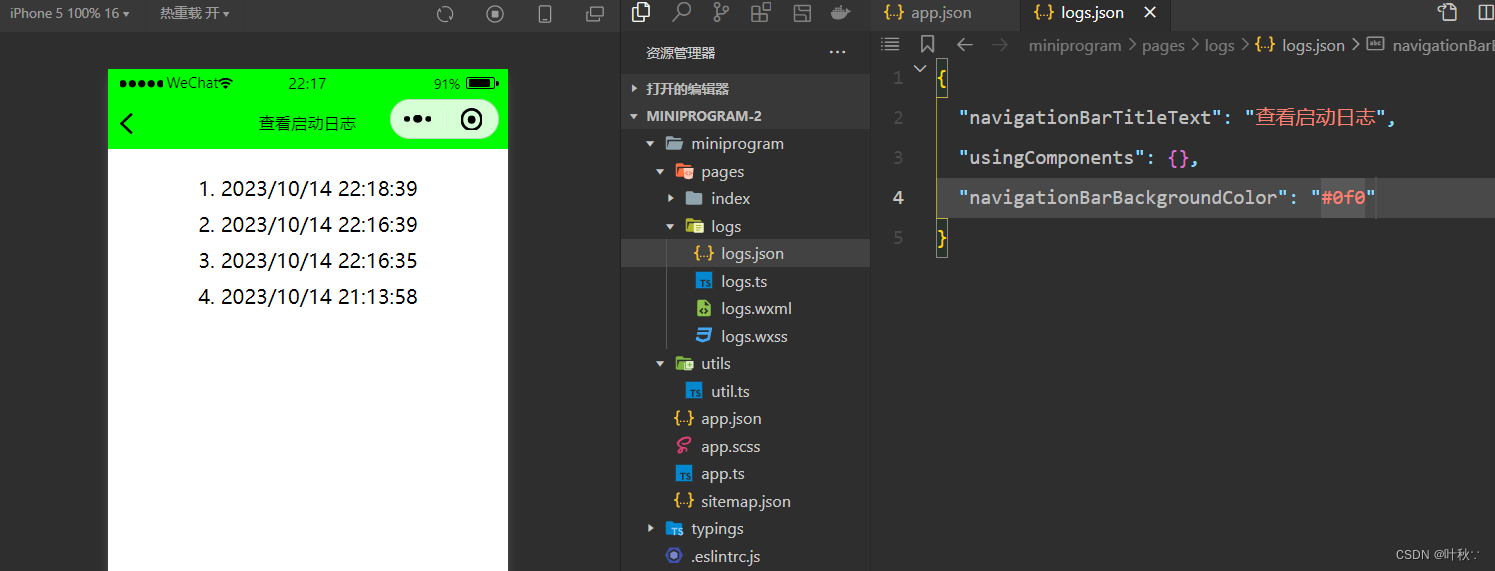
user.json
{"usingComponents": {},"navigationBarTitleText": "用户界面"
}
user.scss
/* pages/user/user.wxss */
.userinfo{color: #0000ff;;
}
user.ts
/* pages/user/user.wxss */
.userinfo{color: #0000ff;;
}
user.wxml
<!--pages/user/user.wxml-->
<view class="container"><view class="userinfo">用户信息:{{userName}}<button bindtap="fun1">点击</button></view>
</view>
总结
本篇博客主要介绍了小程序在电商领域的应用与前景。通过对小程序的简介、电商演示和入门案例进行探讨,希望读者能够深入理解小程序的特点和优势,并在实际应用中发挥其潜力,推动电商行业的进一步发展。
相关文章:

“小程序:改变电商行业的新趋势“
目录 引言1. 小程序的简介1.1 什么是小程序?1.2 小程序的优势 2. 小程序之电商演示1.注册微信小程序2.安装开发工具3.创建项目 3. 小程序之入门案例总结 引言 随着移动互联网的迅猛发展,小程序作为一种全新的应用形态,正在逐渐改变着传统电商…...
创建图案填充)
Python与CAD系列基础篇(五)创建图案填充
目录 0 简述1 win32com2 ezdxf0 简述 本篇详细介绍使用①pyautocadpyautocad本质是调用接口连接autocad,由于此处未找到正确的填充函数,通过win32com库找到相应填充函数,测试发现更为好用,因此后续将用win32com代替pyautocad连接AutoCAD进行处理 ②通过ezdxf处理dxf格式文…...

终端仿真软件连接交换机调试步骤
背景: 通过一台电脑,连接交换机的console口进行命令行调试; 需要用到终端仿真软件以图形界面显示交换机的命令; 本文以华为交换机和华为提供的终端仿真软件IPOP V4.02为例,其他仿真软件应该类似,可模仿。…...

redis基本数据类型
一) 字符串(String) String是redis最基本的类型,value最大是512M,String类型是二进制安全的,可以包含任何数据,如jpg图片或者序列化的对象 1 使用场景 1) 缓存:redis作为缓存层,mysql做持久化层࿰…...

C++笔记之std::async的用法
C笔记之std::async的用法 code review! 文章目录 C笔记之std::async的用法1.概念2.C 异步任务的使用示例 - 使用 std::async 和 std::future3. std::launch::async 和 std::launch::deferred4.如果需要真正的异步,请指定std::launch::async 1.概念 std::async 是 …...

OpenCV4(C++)—— 图像连通域的详细分析
文章目录 前言一、connectedComponents函数二、connectedComponentsWithStats函数 前言 图像连通域,其实就是图像分割的一种方法。它通过检测像素之间的连接关系和相似性来划分图像中的区域,以便进行后续处理。图像邻域和图像邻域分析就不介绍了&#x…...

Rule-Engine-Starter V1.0.0
一个轻量级的规则引擎、搜索引擎,让条件匹配简单、优雅。 GIT地址 https://gitcode.cosmoplat.com/15011240224/rule-engine-starter 介绍 Rule-Engine-Starter 是一个轻量级规则引擎,V1.0.0主要解决条件匹配问题。比如飞书文档,每个文档都…...
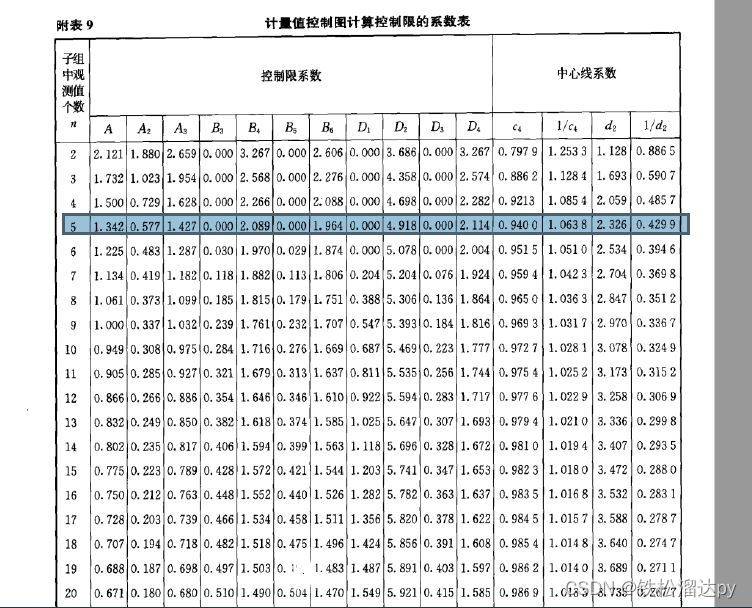
绘制X-Bar-S和X-Bar-R图,监测过程,计算CPK过程能力指数
X-Bar-S图和X-Bar-R图是统计质量控制中常用的两种控制图,用于监测过程的稳定性和一致性。它们的主要区别在于如何计算和呈现数据的变化以及所关注的问题类型。 X-Bar-S图(平均值与标准偏差图): X-Bar代表样本均值,S代表…...

【每日一句】只出现一次的数
文章目录 Tag题目来源题目解读解题思路方法一:位运算 其他语言Cpython3 写在最后 Tag 【位运算-异或和】【数组】【2023-10-14】 题目来源 136. 只出现一次的数字 题目解读 给你一个数组,找出数组中只出现一次的元素。题目保证仅有一个元素出现一次&a…...

GDB调试程序常用命令
编译文件 g -g -o test test.cpp(注意:GDB调试的前提是在编译时加上-g参数.) 启动gdb # 方法一 gdb test # 方法二 gdb file test 设置断点 tbreak:设置临时断点,仅在第一次触发后失效。 watch:设置观察点,监控变量的…...

C语言,求两个数的二进制表达中,有多少个位数不同
以前我的博客中写过一篇求二进制的1的个数的博客,里面用按位与1的方式来判断位数是否为一。 如代码所示: #include <stdio.h> int num(int n) {int a 0;int i 0;while (i < 32){a a (n & 1);n n >> 1;i;}return a; } int main…...

解决Win10电脑无线网卡的移动热点无法开启问题
一、目的 利用无线网卡连接网络,然后又用无线网卡通过移动热点分享该网络。 移动热点,简单地说,就是将台式机或笔记本的 Internet 连接转化成 WIFI 信号以供移动设备无线上网的功能,硬件前提是电脑须安装有无线网卡。 二、问题 …...
Spring framework Day10:JSR330注入注解
前言 JSR330是Java社区标准化进程(Java Community Process,简称JCP)中的一个规范,全名为"Dependency Injection for Java",即Java的依赖注入规范。它定义了一组注解和相关的规范,用于实现依赖注…...

Java开发中List数据量大,需要分片批次处理
在开发过程中可能会遇到需要处理的List数据量过大,可以选择分批处理的方式对大量数据进行处理。 1、使用 apache 的工具包 <dependency><groupId>org.apache.commons</groupId><artifactId>commons-collections4</artifactId><v…...

Apache Doris 2.0.2 版本正式发布!
峰会官网已上线,最新议程请关注:doris-summit.org.cn 点击报名 亲爱的社区小伙伴们,Apache Doris 2.0.2 版本已于 2023 年 10 月 6 日正式发布,该版本对多个功能进行了更新优化,旨在更好地满足用户的需求。有 92 位贡献…...

transformers架构实现
目录 架构代码如下 模型打印如下 架构代码如下 import numpy as np from torch.autograd import Variable import copy from torch import softmax import math import torch import torch.nn.functional as F import torch.nn as nn # 构建Embedding类来实现文本嵌入层 class…...

C++类型推导
这里对C的类型推导方式进行一次全面的总结。 C中有三种类型推导的方式,分别是模板、auto以及decltype()。以下分别介绍这三种方式的同异。 一 模板 假设有这样的函数模板和这样的调用: template<typename T> void f(ParamType param);f(expr);…...
 SVD分解求两个点云的变换矩阵)
Open3D(C++) SVD分解求两个点云的变换矩阵
目录 一、算法原理二、代码实现三、结果展示四、相关链接一、算法原理 计算两个点云的质心计算中心化向量计算协方差矩阵奇异值分解,求解旋转矩阵 R R R计算平移向量 t t...

rtmp htttp推流Windows桌面到srs进行播放
推流命令: ffmpeg -f gdigrab -framerate 30 -i desktop -c:v libx264 -preset ultrafast -tune zerolatency -pix_fmt yuv420p -f flv rtmp://xxx.xxx.xxxx.xx/live/livestream 后面是推流地址 推流后的播放地址为: http://xxxxxx:8080/live/livestream.flv 可以写一个…...

NSSCTF做题(9)
[GDOUCTF 2023]<ez_ze> 看见输入框而且有提示说是ssti注入 输入{{7*7}} 试试,发现报错 输入{%%}发现了是jinja2模板 找到关键函数 Python SSTI利用jinja过滤器进行Bypass ph0ebuss Blog 原理见这篇文章,这里直接给出payload {%set ninedict(aaa…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
