rtmp htttp推流Windows桌面到srs进行播放
推流命令：
ffmpeg -f gdigrab -framerate 30 -i desktop -c:v libx264 -preset ultrafast -tune zerolatency -pix_fmt yuv420p -f flv rtmp://xxx.xxx.xxxx.xx/live/livestream后面是推流地址
推流后的播放地址为：
http://xxxxxx:8080/live/livestream.flv
可以写一个网页来进行播放flv：
<!DOCTYPE html>
<html>
<head><title>FLV Video Player</title><!-- 引入flv.js库 --><script src="https://cdn.jsdelivr.net/npm/flv.js@latest"></script>
</head>
<body><video id="video" controls></video><script>if (flvjs.isSupported()) {var videoElement = document.getElementById('video');var flvPlayer = flvjs.createPlayer({type: 'flv'相关文章：
rtmp htttp推流Windows桌面到srs进行播放
推流命令： ffmpeg -f gdigrab -framerate 30 -i desktop -c:v libx264 -preset ultrafast -tune zerolatency -pix_fmt yuv420p -f flv rtmp://xxx.xxx.xxxx.xx/live/livestream 后面是推流地址 推流后的播放地址为： http://xxxxxx:8080/live/livestream.flv 可以写一个…...
NSSCTF做题（9）
[GDOUCTF 2023]<ez_ze> 看见输入框而且有提示说是ssti注入 输入{{7*7}} 试试，发现报错 输入{%%}发现了是jinja2模板 找到关键函数 Python SSTI利用jinja过滤器进行Bypass ph0ebuss Blog 原理见这篇文章，这里直接给出payload {%set ninedict(aaa…...
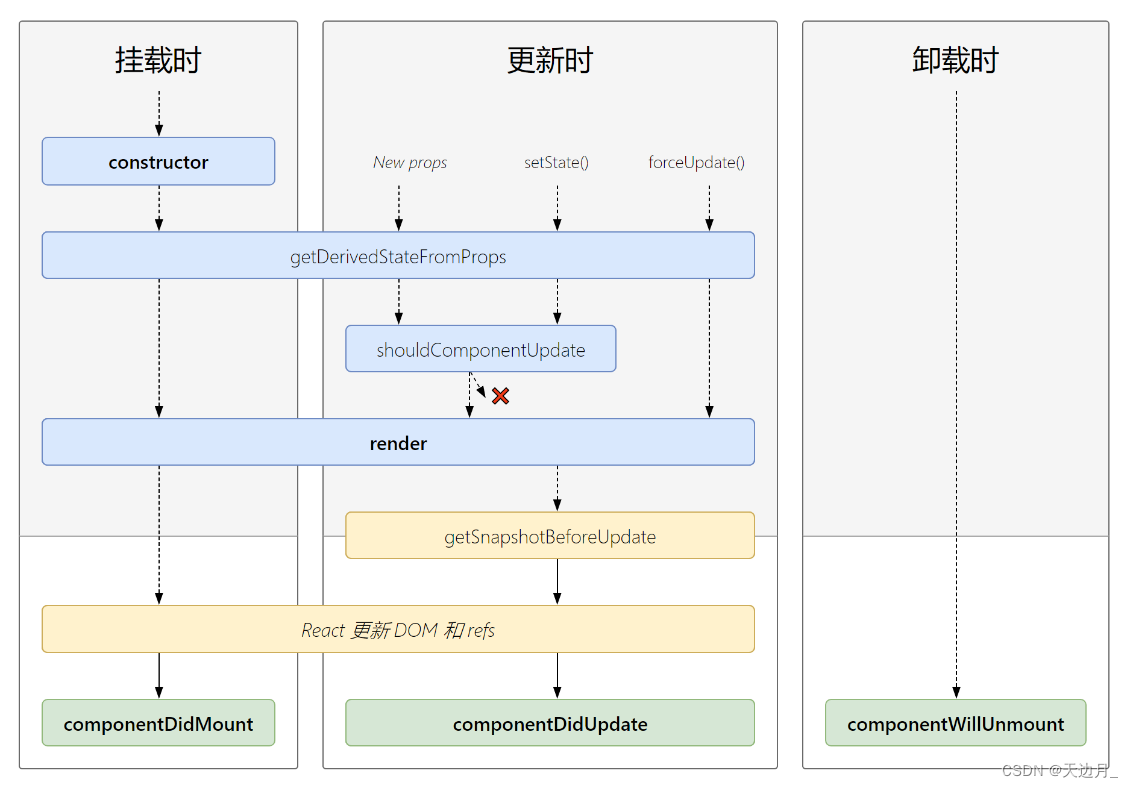
【09】基础知识：React组件的生命周期
组件从创建到死亡它会经历一些特定的阶段。 React 组件中包含一系列勾子函数（生命周期回调函数 <> 生命周期钩子函数 <> 生命周期函数 <> 生命周期钩子），会在特定的时刻调用。 我们在定义组件时，会在特定的生…...
Pytorch之ConvNeXt图像分类
文章目录 前言一、ConvNeXt设计决策1.设计方案2.Training Techniques3.Macro Design🥇Changing stage compute ratio🥈Change stem to "Patchify" 4.ResNeXt-ify5. Inverted Bottleneck6.Large Kernel Size7.Micro Design✨Replacing ReLU wit…...
Linux系统编程：makefile以及文件系统编程
增量编译概念 首先回顾一下我们之前写的各种gcc指令用来执行程序： 可以看见非常繁琐，两个文件就要写这么多，那要是成百上千岂不完蛋。 所以为了简化工作量，很自然的想到了将这些命令放在一起使用脚本文件来一键执行，…...
《动手学深度学习 Pytorch版》 8.5 循环神经网络的从零开始实现
%matplotlib inline import math import torch from torch import nn from torch.nn import functional as F from d2l import torch as d2lbatch_size, num_steps 32, 35 train_iter, vocab d2l.load_data_time_machine(batch_size, num_steps) # 仍然使用时间机器数据集8.…...
写一个宏，可以将一个整数的二进制位的奇数位和偶数位交换
我们这里是利用按位与来计算的 我们可以想想怎么保留偶数上的位？我们可以利用0x55555555按位与上这个数就保留了偶数 我们知道，16进制0x55555555转换为二进制就是0x01010101010101010101010101010101 我们知道，二进制每一位，如…...
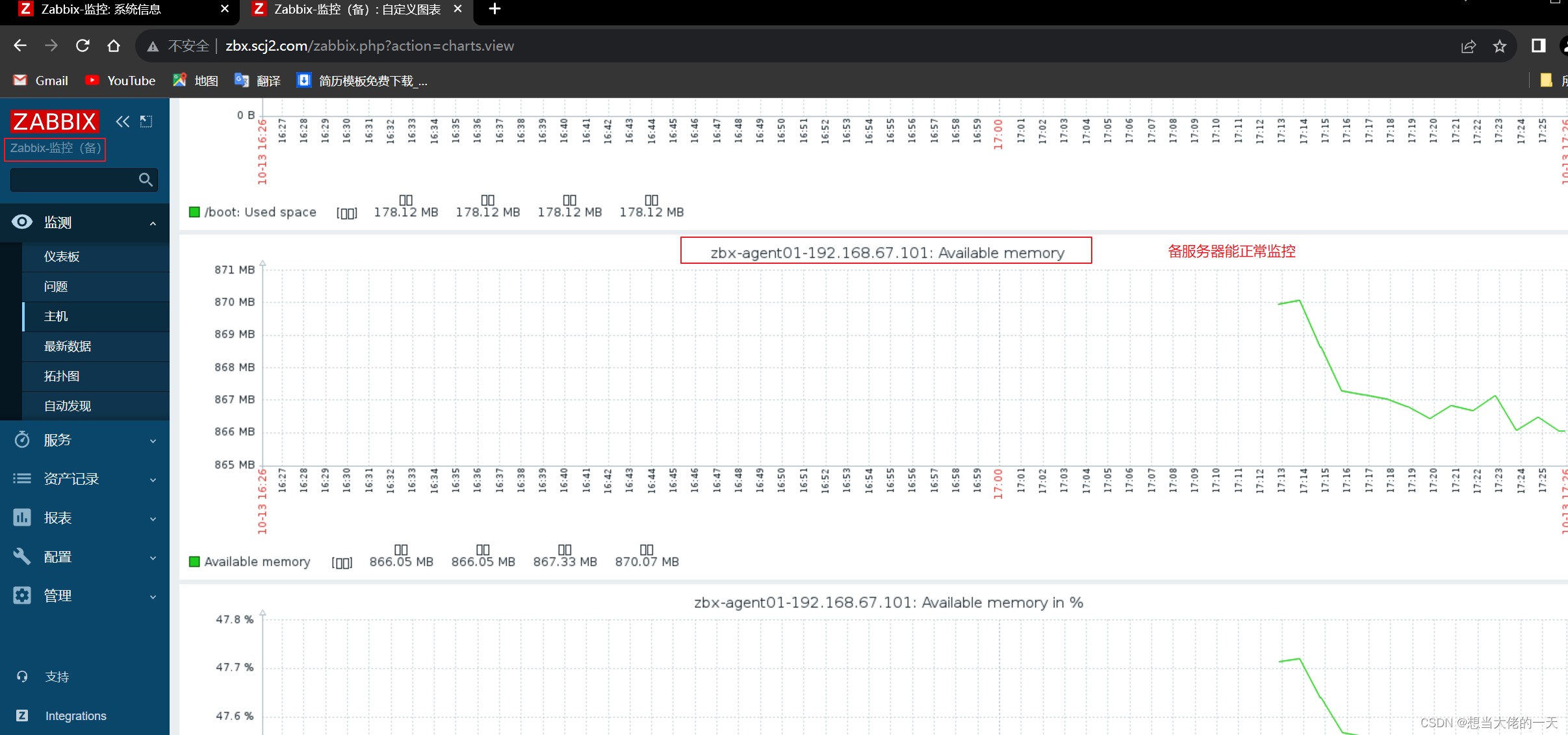
Zabbix监控系统详解2：基于Proxy分布式实现Web应用监控及Zabbix 高可用集群的搭建
文章目录 1. zabbix-proxy的分布式监控的概述1.1 分布式监控的主要作用1.2 监控数据流向1.3 构成组件1.3.1 zabbix-server1.3.2 Database1.3.3 zabbix-proxy1.3.4 zabbix-agent1.3.5 web 界面 2. 部署zabbix代理服务器2.1 前置准备2.2 配置 zabbix 的下载源，安装 za…...
docker 安装oracle
拉取镜像 拉取oracle_11g镜像 拉取oracle镜像(oracle 11.0.2 64bit 企业版 实例名: helowin) Oracle主要在Docker基础上安装，安装环境注意空间和内存，Oracle是一个非常庞大的一个软件， 建议使用网易镜像或阿里镜像网站这里以oracle 11.0.2…...
C++ vector 自定义排序规则（vector＜vector＜int＞＞、vector＜pair＜int,int＞＞）
vector< int > vector<int> vec{1,2,3,4};//默认从小到大排序 1234 sort(vec.begin(),vec.end()); //从大到小排序 4321 sort(vec.begin(),vec.end(),greater<int>());二维向量vector<vector< int >> vector<vector<int>> vec{{0…...
机器学习 Q-Learning
对马尔可夫奖励的理解 看的这个教程 公式：V(s) R(s) γ * V(s’) V(s) 代表当前状态 s 的价值。 R(s) 代表从状态 s 到下一个状态 s’ 执行某个动作后所获得的即时奖励。 γ 是折扣因子，它表示未来奖励的重要性，通常取值在 0 到 1 之间。…...
产品设计心得体会 优漫动游
产品设计需要综合考虑用户需求、市场需求和技术可行性，从而设计出能够满足用户需求并具有市场竞争力的产品。以下是我在产品设计方面的心得体会： 产品设计心得体会 1.深入了解用户需求：在产品设计之前，需要进行充分的用户调研…...
前端--CSS
文章目录 CSS的介绍 引入方式 代码风格 选择器 复合选择器 (选学) 常用元素属性 背景属性 圆角矩形 Chrome 调试工具 -- 查看 CSS 属性 元素的显示模式 盒模型 弹性布局 一、CSS的介绍 层叠样式表 (Cascading Style Sheets). CSS 能够对网页中元素位置的排版进行像素级精…...
实操指南|如何用 OpenTiny Vue 组件库从 Vue 2 升级到 Vue 3
前言 根据 Vue 官网文档的说明，Vue2 的终止支持时间是 2023 年 12 月 31 日，这意味着从明年开始： Vue2 将不再更新和升级新版本，不再增加新特性，不再修复缺陷 虽然 Vue3 正式版本已经发布快3年了，但据我了…...
系统架构设计：15 论软件架构的生命周期
目录 一 软件架构的生命周期 1 需求分析阶段 2 设计阶段 3 实现阶段 4 构件组装阶段...
金山wps golang面试题总结
简单自我介绍如果多个协程并发写map 会导致什么问题如何解决（sync.map，互斥锁，信号量）chan 什么时候会发生阻塞如果 chan 缓冲区满了是阻塞还是丢弃还是panicchan 什么时候会 panic描述一下 goroutine 的调度机制goroutine 什么时…...
计算机视觉实战--直方图均衡化和自适应直方图均衡化
计算机视觉 文章目录 计算机视觉前言一、直方图均衡化1.得到灰度图2. 直方图统计3. 绘制直方图4. 直方图均衡化 二、自适应直方图均衡化1.自适应直方图均衡化（AHE）2.限制对比度自适应直方图均衡化（CRHE）3.读取图片4.自适应直方图均…...
501. 二叉搜索树中的众数
501. 二叉搜索树中的众数 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val0, leftNone, rightNone): # self.val val # self.left left # self.right right class Solution:def findMode(self, root: Option…...
【Linux】常用命令
目录 文件解压缩服务器文件互传scprsync 进程资源网络curl发送简单get请求发送 POST 请求发送 JSON 数据保存响应到文件 文件 ls,打印当前目录下所有文件和目录; ls -l,打印每个文件的基本信息 pwd,查看当前目录的路径 查看文件 catless：可以左右滚动阅读more :翻…...
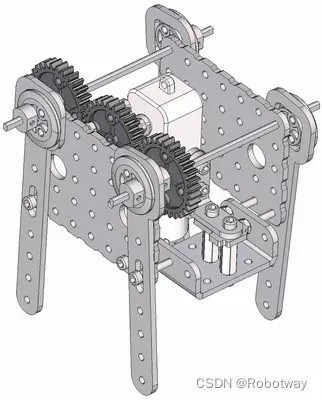
机器人制作开源方案 | 齿轮传动轴偏心轮摇杆简易四足
1. 功能描述 齿轮传动轴偏心轮摇杆简易四足机器人是一种基于齿轮传动和偏心轮摇杆原理的简易四足机器人。它的设计原理通常如下： ① 齿轮传动：通过不同大小的齿轮传动，实现机器人四条腿的运动。通常采用轮式齿轮传动或者行星齿轮传动…...
【Oracle APEX开发小技巧12】
有如下需求： 有一个问题反馈页面，要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据，方便管理员及时处理反馈。 我的方法：直接将逻辑写在SQL中，这样可以直接在页面展示 完整代码： SELECTSF.FE…...
在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能，包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...
在Ubuntu中设置开机自动运行（sudo）指令的指南
在Ubuntu系统中，有时需要在系统启动时自动执行某些命令，特别是需要 sudo权限的指令。为了实现这一功能，可以使用多种方法，包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法，并提供…...
TRS收益互换：跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 （一）概念解析 TRS（Total Return Swap）收益互换是一种金融衍生工具，指交易双方约定在未来一定期限内，基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统，支持多语言对话（如 中文，英文，日语），语音情感（如 开心，悲伤）&#x…...
关于 WASM：1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么？ WebAssembly（WASM） 是一种能在现代浏览器中高效运行的二进制指令格式，它不是传统的编程语言，而是一种 低级字节码格式，可由高级语言（如 C、C、Rust&am…...
让AI看见世界：MCP协议与服务器的工作原理
让AI看见世界：MCP协议与服务器的工作原理 MCP（Model Context Protocol）是一种创新的通信协议，旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天，MCP正成为连接AI与现实世界的重要桥梁。…...
uniapp中使用aixos 报错
问题： 在uniapp中使用aixos，运行后报如下错误： AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
2023赣州旅游投资集团
单选题 1.“不登高山，不知天之高也；不临深溪，不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
Java 二维码
Java 二维码 **技术：**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...