写一个宏,可以将一个整数的二进制位的奇数位和偶数位交换
我们这里是利用按位与来计算的
我们可以想想怎么保留偶数上的位?我们可以利用0x55555555按位与上这个数就保留了偶数
我们知道,16进制0x55555555转换为二进制就是0x01010101010101010101010101010101
我们知道,二进制每一位,如果这个位是0,按位与1还是0,如果这个数是1,按位与1就是1
然后我们把计算的结果<<1,这样偶数上的位就在奇数位上了
奇数位一样的保留方法,我们可以利用0xaaaaaaaa按位与上这个数保留奇数
16进制0xaaaaaaaa转换为二进制就是0x10101010101010101010101010101010
我们把结果>>1,这样奇数位就在偶数位上了
#define SWAP(num) num = ((num&0x55555555)<<1)+((num&0xaaaaaaaa)>>1)
int main()
{int num = 10;//00000000000000000000000000001010 ->10// 其奇偶位交换后得 ://00000000000000000000000000000101 ->5SWAP(num);printf("%d", num);return 0;
}相关文章:

写一个宏,可以将一个整数的二进制位的奇数位和偶数位交换
我们这里是利用按位与来计算的 我们可以想想怎么保留偶数上的位?我们可以利用0x55555555按位与上这个数就保留了偶数 我们知道,16进制0x55555555转换为二进制就是0x01010101010101010101010101010101 我们知道,二进制每一位,如…...
Zabbix监控系统详解2:基于Proxy分布式实现Web应用监控及Zabbix 高可用集群的搭建
文章目录 1. zabbix-proxy的分布式监控的概述1.1 分布式监控的主要作用1.2 监控数据流向1.3 构成组件1.3.1 zabbix-server1.3.2 Database1.3.3 zabbix-proxy1.3.4 zabbix-agent1.3.5 web 界面 2. 部署zabbix代理服务器2.1 前置准备2.2 配置 zabbix 的下载源,安装 za…...
docker 安装oracle
拉取镜像 拉取oracle_11g镜像 拉取oracle镜像(oracle 11.0.2 64bit 企业版 实例名: helowin) Oracle主要在Docker基础上安装,安装环境注意空间和内存,Oracle是一个非常庞大的一个软件, 建议使用网易镜像或阿里镜像网站这里以oracle 11.0.2…...
)
C++ vector 自定义排序规则(vector<vector<int>>、vector<pair<int,int>>)
vector< int > vector<int> vec{1,2,3,4};//默认从小到大排序 1234 sort(vec.begin(),vec.end()); //从大到小排序 4321 sort(vec.begin(),vec.end(),greater<int>());二维向量vector<vector< int >> vector<vector<int>> vec{{0…...

机器学习 Q-Learning
对马尔可夫奖励的理解 看的这个教程 公式:V(s) R(s) γ * V(s’) V(s) 代表当前状态 s 的价值。 R(s) 代表从状态 s 到下一个状态 s’ 执行某个动作后所获得的即时奖励。 γ 是折扣因子,它表示未来奖励的重要性,通常取值在 0 到 1 之间。…...

产品设计心得体会 优漫动游
产品设计需要综合考虑用户需求、市场需求和技术可行性,从而设计出能够满足用户需求并具有市场竞争力的产品。以下是我在产品设计方面的心得体会: 产品设计心得体会 1.深入了解用户需求:在产品设计之前,需要进行充分的用户调研…...

前端--CSS
文章目录 CSS的介绍 引入方式 代码风格 选择器 复合选择器 (选学) 常用元素属性 背景属性 圆角矩形 Chrome 调试工具 -- 查看 CSS 属性 元素的显示模式 盒模型 弹性布局 一、CSS的介绍 层叠样式表 (Cascading Style Sheets). CSS 能够对网页中元素位置的排版进行像素级精…...
实操指南|如何用 OpenTiny Vue 组件库从 Vue 2 升级到 Vue 3
前言 根据 Vue 官网文档的说明,Vue2 的终止支持时间是 2023 年 12 月 31 日,这意味着从明年开始: Vue2 将不再更新和升级新版本,不再增加新特性,不再修复缺陷 虽然 Vue3 正式版本已经发布快3年了,但据我了…...

系统架构设计:15 论软件架构的生命周期
目录 一 软件架构的生命周期 1 需求分析阶段 2 设计阶段 3 实现阶段 4 构件组装阶段...

金山wps golang面试题总结
简单自我介绍如果多个协程并发写map 会导致什么问题如何解决(sync.map,互斥锁,信号量)chan 什么时候会发生阻塞如果 chan 缓冲区满了是阻塞还是丢弃还是panicchan 什么时候会 panic描述一下 goroutine 的调度机制goroutine 什么时…...

计算机视觉实战--直方图均衡化和自适应直方图均衡化
计算机视觉 文章目录 计算机视觉前言一、直方图均衡化1.得到灰度图2. 直方图统计3. 绘制直方图4. 直方图均衡化 二、自适应直方图均衡化1.自适应直方图均衡化(AHE)2.限制对比度自适应直方图均衡化(CRHE)3.读取图片4.自适应直方图均…...

501. 二叉搜索树中的众数
501. 二叉搜索树中的众数 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val0, leftNone, rightNone): # self.val val # self.left left # self.right right class Solution:def findMode(self, root: Option…...

【Linux】常用命令
目录 文件解压缩服务器文件互传scprsync 进程资源网络curl发送简单get请求发送 POST 请求发送 JSON 数据保存响应到文件 文件 ls,打印当前目录下所有文件和目录; ls -l,打印每个文件的基本信息 pwd,查看当前目录的路径 查看文件 catless:可以左右滚动阅读more :翻…...
机器人制作开源方案 | 齿轮传动轴偏心轮摇杆简易四足
1. 功能描述 齿轮传动轴偏心轮摇杆简易四足机器人是一种基于齿轮传动和偏心轮摇杆原理的简易四足机器人。它的设计原理通常如下: ① 齿轮传动:通过不同大小的齿轮传动,实现机器人四条腿的运动。通常采用轮式齿轮传动或者行星齿轮传动…...
Windows中将tomcat以服务的形式安装,然后在服务进行启动管理
Windows中将tomcat以服务的形式安装,然后在服务进行启动管理 第一步: 在已经安装好的tomcat的bin目录下: 输入cmd,进入命令窗口 安装服务: 输入如下命令,最后是你的服务名,避免中文和特殊字符 service.…...
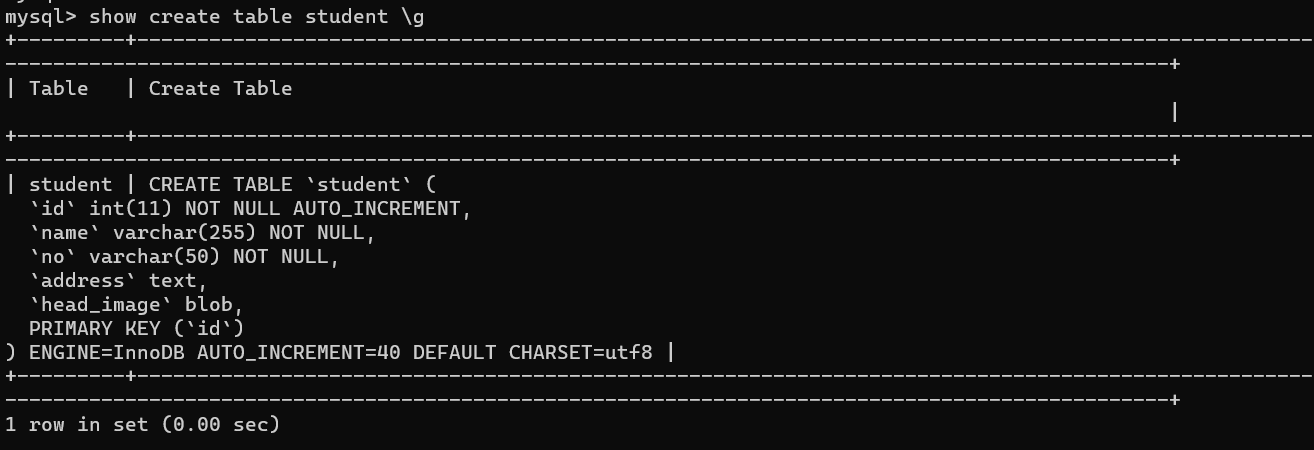
解决ERROR: No query specified的错误以及\G 和 \g 的区别
文章目录 1. 复现错误2. 分析错误3. 解决问题4. \G和\g的区别 1. 复现错误 今天使用powershell连接数据库后,执行如下SQL语句: mysql> select * from student where id 39 \G;虽然成功查询除了数据,但报出如下错误的信息: my…...

mysql中SUBSTRING_INDEX函数用法详解
MySQL中的SUBSTRING_INDEX函数用于从字符串中提取子字符串,其用法如下: SUBSTRING_INDEX(str, delim, count)参数说明: str:要提取子字符串的原始字符串。delim:分隔符,用于确定子字符串的位置。count&am…...

AndroidStudio报错:android.support.v4.app.Fragment
解决办法一 android.support.v4.app.Fragment替换为android.app.Fragment 解决办法二 有时太多,先类型过去再说。 找到gradle.properties,修改: android.useAndroidXfalse android.enableJetifierfalse...
今年这情况,还能不能选计算机了?
在知乎上看到一个有意思的问题,是劝退计算机的。 主要观点: 计算机从业人员众多加班,甚至需要99635岁危机秃头 综上所属,计算机不仅卷,而且还是一个高危职业呀,可别来干了。 关于卷 近两年确实能明显感觉…...

Elastic Cloud v.s. Zilliz Cloud:性能大比拼
Elastic Cloud v.s. Zilliz Cloud:性能大比拼 Zilliz 经常会收到来自开发者和架构师的提问:“Zilliz Cloud 和 Elastic Cloud 比起来,谁进行向量处理能力比较强?” 诸如此类的问题很多,究其根本,大都是开发者/架构师在为语义相似性检索系统进行数据库选型时缺少决策依据有…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
