2023面试必备:web自动化测试POM设计模式详解

1.背景
为UI页面写自动化测试用例时(如:web自动化、app自动化),使用普通的线性代码,测试用例中会存在大量的元素定位及操作细节,当UI界面变化时,测试用例也要跟着变化,在自动化测试用例增加时,用例将难以维护。那么有没有一个方法能够降低UI自动化测试用例的维护难度呢?PageObject设计模式(简称PO模式)很好的解决了这个问题
2.PO简介
PO是PageObject设计模式的简称,有时也称为POM,中文含义:页面对象模型,用于专门对一个系统进行自动化测试实现的设计模式。可以最大程度实现测试的覆盖率,是目前业内公认的最佳设计模式。
3.理解PO模式
我们知道做UI自动化时,就是使用自动化的方式对页面元素进行相关的操作,业务流程就是通过对不同UI页面进行操作、跳转,从而构成我们的主体业务流程。PO模式就是以每个页面为对象主体作为自动化测试的执行对象,来实现整体的自动化测试。下面我们以添加商品到用户购物车为例进行普通思路与PO模式的对比帮助大家进一步理解PO模式
添加商品到购物车的测试---普通模式输入url-->点击登录-->输入账号-->输入密码
-->点击登录按钮-->搜索商品-->选择商品-->
选择商品属性-->点击加入购物车---PO模式进入登录页,执行登录操作进入商品详情页,执行添加商品到购物车操作进入购物车页面,执行校验添加是否成功操作
从上面的对比,我们发现PO模式基于系统的模块页面定义不同的页面对象,来实现不同页面的一个或者多个操作行为;再基于多个页面对象的操作行为进行组装,实现一个完整的系统业务流程
4.如何实现
4.1 PO模式的工程结构
PO模式在实现时,基本上可以分为四层:基类、页面对象类、测试数据类、测试用例类;通过分层架构的思想,实现测试用例与测试数据的分离、业务代码与测试代码的分离,具体每层的作用如下:
基类(base_page):封装各类行为操作,便于测试页面对象类进行调用,是整个PO模式体系的底层实现
页面对象类(obj_page):提取系统中的关键页面,封装成页面对象;主要页面的元素封装为页面对象类的属性,将页面的操作行为封装为页面对象类的方法
测试数据类(case_data):管理测试数据
测试用例类(test_cases):组装各页面对象类的行为,形成完成的业务流程进行测试
具体的工程图例如下:

4.2 工程代码
下面以ecshop项目为例演绎整体的框架设计思路
a.基类的包下创建一个basepage.py文件,里面封装底层的基础操作及公共方法,详细代码如下:
from selenium import webdriver
from time import sleepclass BasePage:#初始化def __init__(self,brow_type):try:driver = getattr(webdriver, brow_type)()except:driver = getattr(webdriver, 'Chrome')()driver.maximize_window()self.driver = driver#封装get方法def get(self,url):self.driver.get(url)#封装定位页面元素的方法def locator(self,locator):return self.driver.find_element(*locator)#封装input方法def input(self,locator,input_value):self.locator(locator).send_keys(input_value)#封装close方法def close(self):self.driver.close()#封装quit方法def quit(self):self.driver.quit()#封装click方法def click(self,locator):self.locator(locator).click()#封装强制等待方法def sleep(self,sec):sleep(sec)
b.页面对象类的包下为每个页面对象创建一个页面对象的.py文件,这里我们举例创建一个login_page.py文件,详细代码如下:
from base_page.basepage import BasePageclass LoginPage(BasePage):'''页面对象类继承于基类页面元素类对象1.页面url:封装为页面对象类的属性2.页面元素:封装为页面对象类的属性3.页面功能:封装页面对象类的方法'''#1.页面urldefault_url = r'http://192.168.53.213/ecshop'login_url = r'/user.php'url = default_url + login_url#2.页面元素username = ('name','username')password = ('name','password')click_locator = ('name','submit')#3.页面功能def login(self,user,pwd):self.get(self.url)self.input(self.username,user)self.input(self.password,pwd)self.click(self.click_locator)
c.在测试数据类的包下面使用yaml格式数据管理测试用例数据,数据具体内容如下:

d.测试用例类的包下创建test_开头的测试用例.py文件,这里我们举例创建一个test_login.py文件,详细代码如下:
**import unittest
from ddt import ddt,file_data
from obj_page.login_page import LoginPage@ddt
class TestLogin(unittest.TestCase):#前置处理:创建登录页面对象def setUp(self) -> None:self.loginpage = LoginPage('Chrome')#后置处理:退出浏览器def tearDown(self) -> None:self.loginpage.quit()#测试登录,结合ddt+yaml进行数据驱动处理 @file_data('../case_data/login.yaml')def test_login(self,user,pwd,locator,except_value):self.loginpage.login(user,pwd)#登录self.assertEqual(self.loginpage.locator(eval(locator)).text,except_value)#断言if __name__ == '__main__':unittest.main()
4.3 执行测试用例查看结果
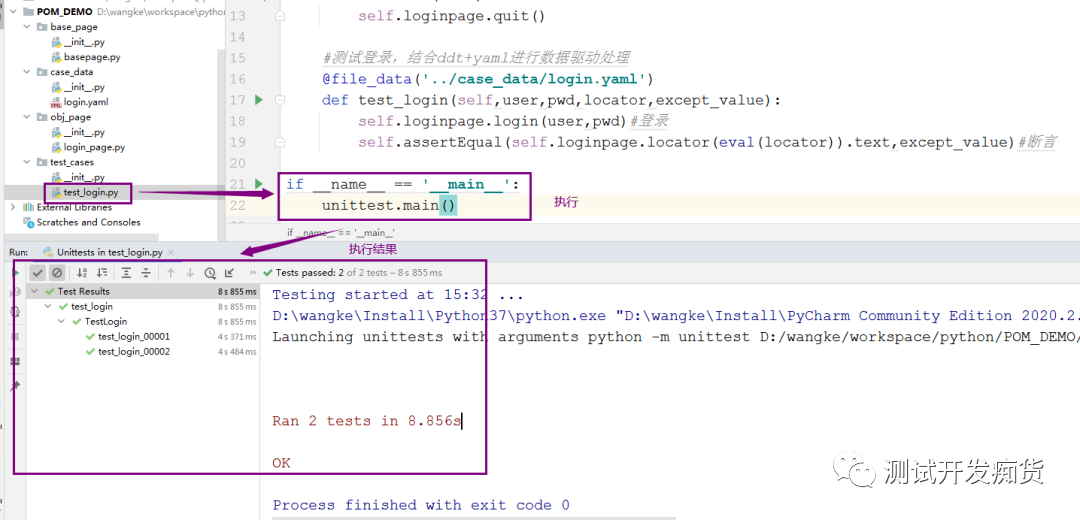
4.4 这样设计具体优点
a.当登录页面的页面元素位置变化时,我们只需要在页面对象类中去具体修改具体页面对应的元素即可,不需要去修改测试用例的内容,如下图:
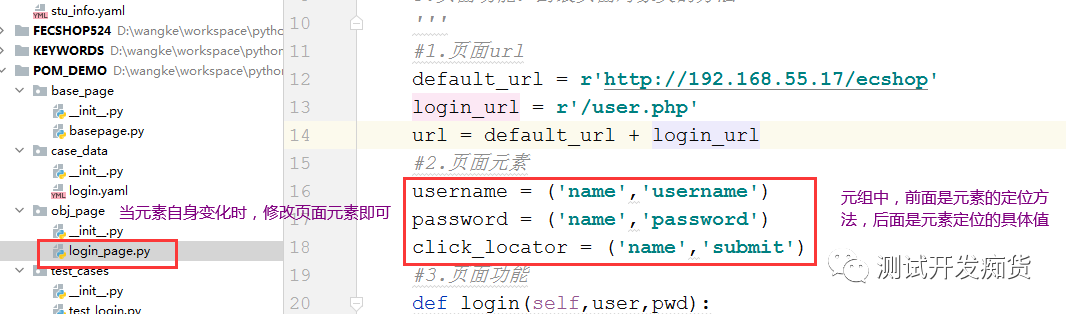
b.当登录的业务流程变化时,比如要加上勾选协议条款等必选操作时,我们只需要在页面对象类中去修改具体对应的操作行为即可,不需求做其它任何修改,如下图:
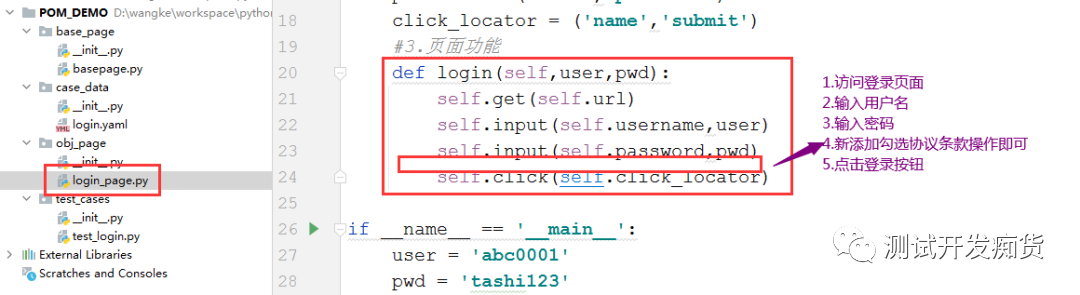
c.我们要测试登录的多种场景时,只需要去测试用例数据管理类中找到对应的数据管理文档,修改或添加测试用例数据即可,不需求做其它任何操作,大大的提高了代码的复用性,如下图:

d.对于相互依赖的复杂业务场景,当业务流程变化时,我们只需要修改测试用例对于各页面对象类行为方法的组装过程,受流程影响的测试数据同步修改即可,不需求修改其它的地方。如下图:
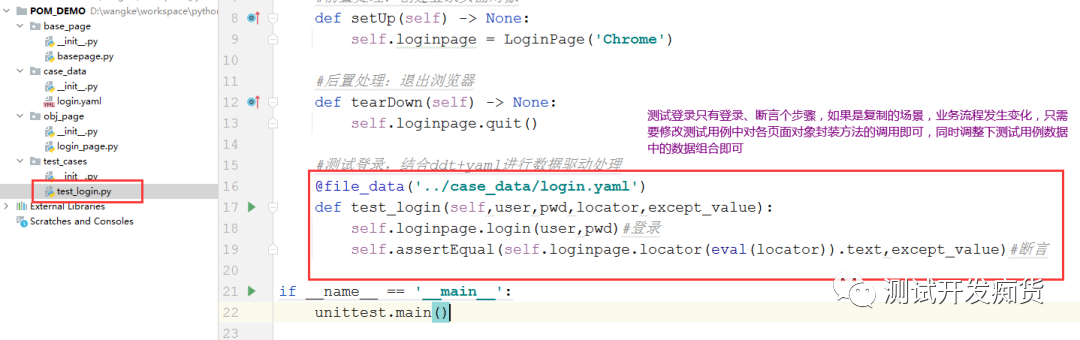
5.PO模式设计总结
a.公共方法代表页面提供的服务
b.不要暴露页面细节,对外只提供方法名
c.不要把断言和操作细节混用,操作细节中不要使用断言,可以把断言放到单独的模块中,如:testcase中
d.页面对象类的方法可以return到新打开的页面,点击一个页面可能会产生新的页面,可以使用return表示跳转,或者通过页面url直接访问
e.不要把整页内容都放到PO中,只为页面中重要的内容进行封装,对不重要的内容进行舍弃
f.相同的行为会产生不同的结果,可以封装不同的接口;如点击登录可能成功,也可能失败,你可以封装为不同的方法;也可以借用测试用例数据来处理
g.UI自动测试以流程测试为主,不是为了所以的细节全部实现自动化
如果文章对你有帮助,记得点赞,收藏,加关注。会不定期分享一些干货哦......
最后感谢每一个认真阅读我文章的人,看着粉丝一路的上涨和关注,礼尚往来总是要有的,虽然不是什么很值钱的东西,如果你用得到的话可以直接拿走:
这些资料,对于想做【软件测试】的朋友来说应该是最全面最完整的备战仓库,这个仓库也陪伴我走过了最艰难的路程,希望也能帮助到你!凡事要趁早,特别是技术行业,一定要提升技术功底。希望对大家有所帮助……加入我的学习交流群一起学习交流讨论把!!!!

相关文章:

2023面试必备:web自动化测试POM设计模式详解
1.背景 为UI页面写自动化测试用例时(如:web自动化、app自动化),使用普通的线性代码,测试用例中会存在大量的元素定位及操作细节,当UI界面变化时,测试用例也要跟着变化,在自动化测试…...

【人工智能 AI】Robotic Process Automation (RPA) 机器人流程自动化 (RPA)
目录 ROBOTIC PROCESS AUTOMATION SERVICES机器人流程自动化服务 What is RPA? 什么是机器人流程自动化?...
ubuntu/linux系统知识(37)systemd管理临时文件的方法systemd-tmpfiles
1、systemd-tmpfiles Linux产生大量的临时文件和目录,例如/tmp、/run 。systemd提供了一个结构化的可配置方法来管理临时文件和目录,即systemd-tmpfiles工具和配套的几个服务,以实现创建、删除和管理临时文件。 systemd创建了几个调用syste…...

云计算专业和计算机专业哪个好就业?
云计算专业其实也是属于计算机类专业呢,他包括了计算机硬件设备、计算机网络、磁盘柜、操作系统、中间件、数据库、服务器/虚拟机、应用软件开发等技术内容,云计算技术是以IT服务的形式面向用户的;所以云计算不是一门技术,而是众多…...

electron sha512 checksum mismatch
sha512 checksum mismatch错误 此错误常常发生在electron检查更新时,导致检查更新失败。 自动更新使用的模块 electron-updater or electron-differential-updater win下electron-builder打包 使用electron-builder打包之后,进行版本增量更新遇到的…...
使用Chemistry Development Kit (CDK) 来进行化学SMILES子结构匹配
摘要 SMILES是一种用于描述化合物结构的字符串表示法,其中子结构搜索是在大规模化合物数据库中查找特定的结构。然而,这种搜索方法存在一个误解,即将化合物的子结构视为一个独立的实体进行搜索,而忽略了它们在更大的化合物中的上…...

CMake模块的使用和自定义模块
CMake模块的使用和自定义模块一、前言二、使用Find模块2.1、准备工作2.2、添加头文件路径和库文件2.3、< name >_FOUND 来控制工程特性三、编写自定义的Find模块3.1、 准备工作3.2、cmake 模块3.3、使用自定义的FindHELLO 模块构建工程3.4、如果没有找到hello library四、…...

jvm调优参数配置
在JVM启动参数中,可以设置跟内存、垃圾回收相关的一些参数设置,默认情况不做任何设置JVM会工作的很好,但对一些配置很好的Server和具体的应用必须仔细调优才能获得最佳性能。通过设置我们希望达到一些目标: GC的时间足够的小 GC的…...

Leetcode.1567 乘积为正数的最长子数组长度
题目链接 Leetcode.1567 乘积为正数的最长子数组长度 Rating : 1710 题目描述 给你一个整数数组 nums,请你求出乘积为正数的最长子数组的长度。 一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。 请你返回乘积为正数的最长子数组长度…...
)
部分库与使用方法总结(自用)
1.tqdm tqdm是Python的进度条库,可以在长循环操作中显示进度提示 tqdm.tqdm:传入数字 from tqdm import tqdm for i in tqdm(range(1, 5)):print(i)使用bar_format "{l_bar}{bar}"可以只显示进度条 from tqdm import tqdm for i in tqdm(range(1, 5), ba…...

C++实现日期类
文章目录前言1.日期类的功能分析1.大致分析2.接口设计2.具体实现1.日期类的成员函数和成员变量2.初始化(构造函数)3.对日期进行天数推算4.比较相关的运算符重载5.前置后置自增或自减6.日期相减与流插入流提取1.日期相减2.重载流插入和流提取3.总结前言 之前介绍了C…...
想成为一名专业黑客,但不知道从哪里学起?我来教你。
成为一名黑客需要学什么? 想成为一名专业黑客,但不知道从哪里学起”很多人在后台问过这个问题,今天就为你介绍成为专业黑客必须学习的十个方面的知识,希望能为迷惘中的你指明方向。 想要成为网络hacker黑客?先来学习…...

VMware ESXi 7.0 U3k Unlocker OEM BIOS 集成网卡驱动和 NVMe 驱动 (集成驱动版)
ESXi 7 U3 标准版集成 Intel 网卡、USB 网卡 和 NVMe 驱动 请访问原文链接:https://sysin.org/blog/vmware-esxi-7-u3-sysin/,查看最新版。原创作品,转载请保留出处。 作者主页:www.sysin.org 本次针对 2023-02-21 发布的 ESXi …...

新的计算方法:预测益生菌在不同生长条件下的相互作用
谷禾健康 益生菌可以产生有益的维生素、消化酶、必需氨基酸、免疫调节和抗菌代谢产物,从而促进人体健康,预防肠道炎症性疾病、自身免疫性疾病和胃肠道感染。其宝贵特性已得到健康行业、医疗专业人士和公众的认可。 比起单菌株益生菌,多菌株益…...

python自学之《21天学通Python》(13)——第16章 数据库编程
数据库指的是以一定方式存储在一起、能为多个用户共享、具有尽可能小的冗余度、与应用程序彼此独立的数据集合。而我们平时所说的数据库实际上是包含了数据库管理系统(DBMS)的,数据库管理系统是为管理数据库而设计的软件系统,它一…...

[架构之路-118]-《软考-系统架构设计师》-软架构设计-11-可靠性相关设计
第11节 可靠性相关设计11.1 可靠性基本概念可靠性工程是研究产品生命周期中故障的发生、发展规律,达到预防故障,消灭故障,提高产品可用性的工程技术。信息系统的可靠性是指系统在满足一定条件的应用环境中能够正常工作的能力,可以…...
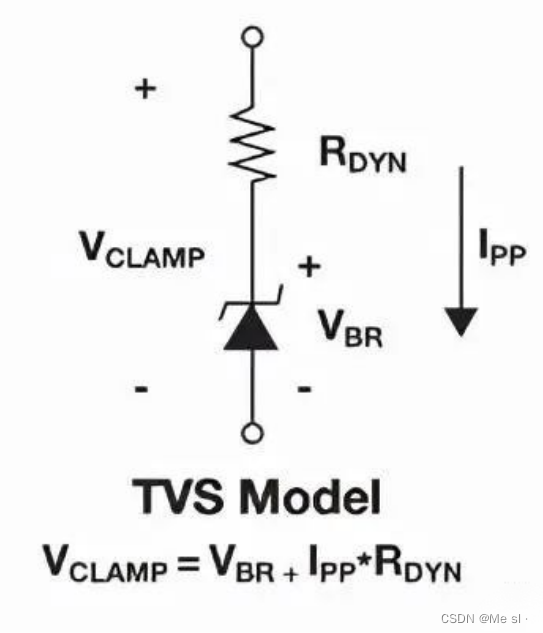
电阻串联的作用
电阻串联常见作用 第一个作用是:阻抗匹配: 因为信号源的阻抗很低,跟信号线之间阻抗不匹配,串上一个电阻后,可以改善匹配情况,以减少反射,避免振荡等。 常见的阻抗匹配方法 1、使用变压器来做…...

leetcode 1675. Minimize Deviation in Array(最小化数组偏差)
数组里面有n个正整数,里面的数字可以无限次进行如下操作: 1.偶数可以除以2 2.奇数可以乘以2 数组中任意两元素差的最大值称为偏差。 把数组中的元素进行上面2种操作,使偏差最小。 思路: 数组中现有2种数字,一种是奇数…...

特征向量中心度(eigenvector centrality)算法原理与源码解析
前言 随着图谱应用的普及,图深度学习技术也逐渐被越来越多的数据挖掘团队所青睐。传统机器学习主要是对独立同分布个体的统计学习,而图深度学习则是在此基础上扩展到了非欧式空间的图数据之上,通过借鉴NLP和CV方向的模型思想,衍生…...
Vue3 中组件的使用(上)
目录前言:一、什么是组件二、注册组件1. 全局注册2. 局部注册二、传递数据【父 -> 子】1. 字符串数组的形式2. 对象的形式三、组件事件【子 -> 父】1. 字符串数组式声明自定义事件2. 【子组件】触发组件事件3. 【父组件】监听子组件自定义事件4. 组件事件例子…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

ubuntu中安装conda的后遗症
缘由: 在编译rk3588的sdk时,遇到编译buildroot失败,提示如下: 提示缺失expect,但是实测相关工具是在的,如下显示: 然后查找借助各个ai工具,重新安装相关的工具,依然无解。 解决&am…...
