动态规划:918. 环形子数组的最大和

个人主页 : 个人主页
个人专栏 : 《数据结构》 《C语言》《C++》《算法》
文章目录
- 前言
- 一、题目解析
- 二、解题思路
- 解题思路
- 状态表示
- 状态转移方程
- 初始化
- 填表顺序
- 返回值
- 三、代码实现
- 总结
前言
本篇文章仅是作为小白的我的一些理解,,如果有错误的地方,希望大佬们指出。
918. 环形子数组的最大和
一、题目解析

求环型数组中连续子数组最大和。
二、解题思路
解题思路
关于子数组的最大和,其有两种情况。
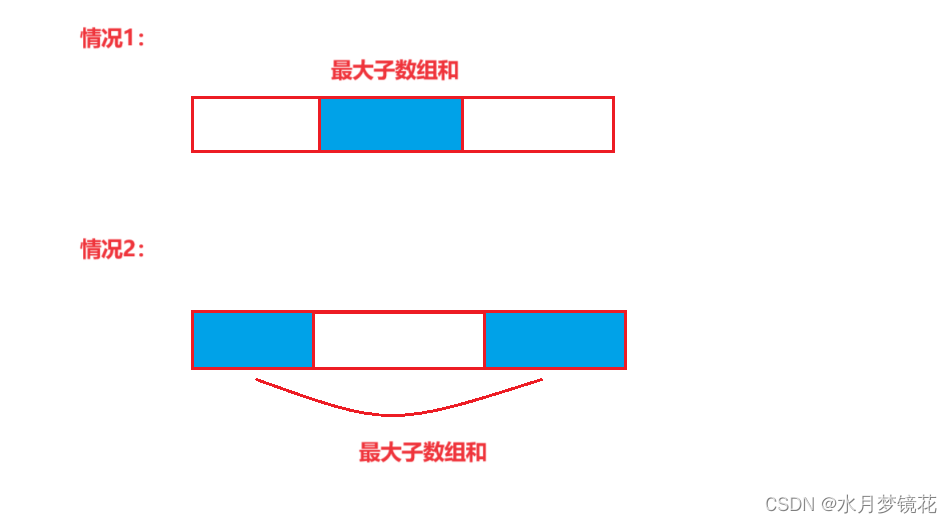
对于情况1而言,我们只需要正常使用dp求最大子数组和即可。
对于情况2而言,如果我们使用前缀和 与 后缀和 求和来求最大子数组和就相对麻烦,但如果我们先求最小子数组和呢?

情况二:求最大子数组和,就可以转换为数组和(sum) - 最小子数组和。
状态表示
该题的状态表示:经验(以该位置为终点 / 以该位置为起点) + 题目要求

那么对于情况1记为 f() ,f [ i ]表示以 i 位置为终点的所以子数组的最大和。
那么对于情况2记为 g(),g [ i ]表示以 i 位置为终点的所以子数组的最小和。
状态转移方程
情况1
对于在数组 i 位置的元素,我们可以将其分成两个状态。
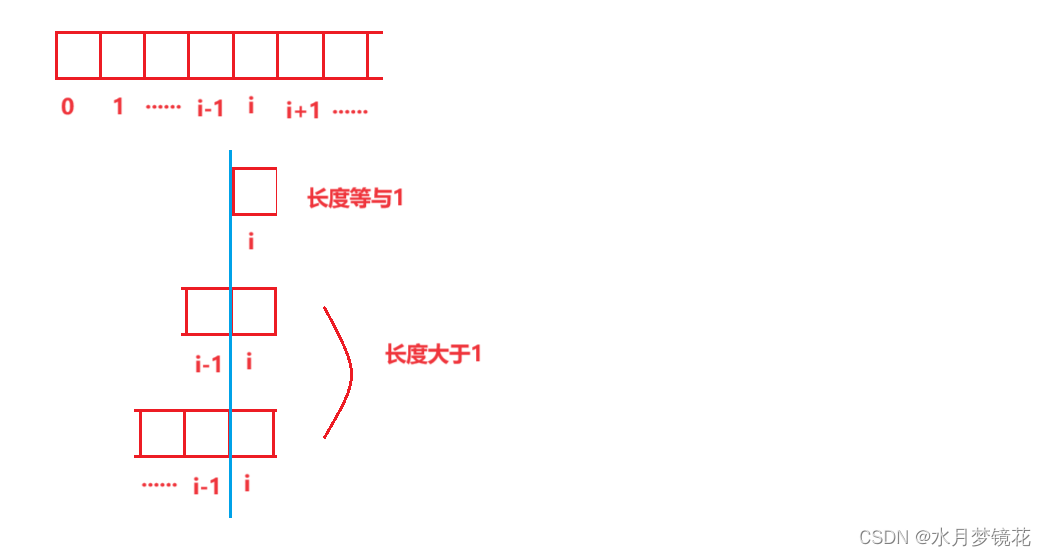
即 f [i]的长度等于1,和 f [i]的长度大于1。
当 f [i]的长度等于1时,此时子数组最大和不就是该元素的大小,即f [i] = nums[i]
当 f [i]的长度大于1时,此时子数组最大和不就是 之前子数组最大和(f[i-1]) + 该元素大小,即f[i] = f[i-1] + nums[i]
那么我们对这两种情况取最大值即可得 f [ i ] 的状态转移方程。

情况2
和情况1类似,对于情况2,我们同样可以以 i位置,分成两种状态。

即 g [i]的长度等于1,和 g [i]的长度大于1。
当 g [i]的长度等于1时,此时子数组最小和不就是该元素的大小,即g [i] = nums[i]
当 g [i]的长度大于1时,此时子数组最小和不就是 之前子数组最小和(g[i-1]) + 该元素大小,即g[i] = g[i-1] + nums[i]
那么我们对这两种状态取最小值,既可以得到 g [i]的状态转移方程

初始化
我们要求 f [i]就要先知道 f [i -1],但如果当 i = 0时,f [i-1]就会越界。那么我们虚拟一块空间,将整个 f[i] 后移一个位置。如下所示:

如果我们进行这样的操作,有两点需要注意。
- 如何填写 f[0]保证后续填表结果正确?
只要f[0] = 0即可,毕竟f[1] = max(f[0], f[0]+nums[0])此时f[0] == f[0] + nums[0] - 映射关系
因为整个f[i]后移了一个,所以f[i] 所对应的元素 nums[i]相对前移了,即f[i] 与 nums[i-1]的元素相对应。
填表顺序
要求f[i],就要先知道f[i-1],那么我们就要从前向后遍历数组nums,来填表。
返回值
我们只需要 返回情况1 与 情况2 的最大值即可。
但对于{-1, -2, -3, -4}而言,情况2 的值是:sum(-10) - gmin(-10)等于0,情况1 的值是:fmax(-1)。那么返回值就是0,结果错误。所以要先判断gmin == sum,如果相等,表示此时数组全是负数,返回fmax即可。如果不相等,返回情况1 与 情况2 的最大值即可。
三、代码实现
class Solution {
public:int maxSubarraySumCircular(vector<int>& nums) {int n = nums.size();vector<int> f(n+1), g(n+1);int fmax = INT_MIN, gmin = INT_MAX, sum = 0;for(int i = 1; i <= n; i++){f[i] = max(f[i-1] + nums[i-1], nums[i-1]);fmax = max(f[i], fmax);g[i] = min(g[i-1] + nums[i-1], nums[i-1]);gmin = min(g[i], gmin);sum += nums[i-1];}return sum == gmin? fmax: max(fmax, sum - gmin);}
};
总结
以上就是我对于环形子数组的最大和的理解。感谢支持!!!

相关文章:

动态规划:918. 环形子数组的最大和
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》《算法》 文章目录 前言一、题目解析二、解题思路解题思路状态表示状态转移方程初始化填表顺序返回值 三、代码实现总结 前言 本篇文章仅是作为小白的我的一些理解,,…...

毅速丨模具3D打印材料有哪些选择
当前1.2709和CX是市面上最常用的3D打印模具钢材料,模具3D打印有没有更多的材料选择呢? 据了解,上海毅速推出的几款3D打印新材料正在被越来越多的行业所采用。如毅速的EM191S高性能高抛光不锈钢粉末,这款材料的抗开裂和耐腐蚀性能是…...
Springcloud笔记(1)-微服务和springcloud介绍
微服务简介 就是将一个大的应用,拆分成多个小的模块,每个模块都有自己的功能和职责,每个模块可以 进行交互,这就是微服务对于微服务,业界没有严格统一的定义,但是作为“微服务”这名词的发明人,…...
十六、代码校验(4)
本章概要 调试 使用 JDB 调试图形化调试器 调试 尽管聪明地使用 System.out 或日志信息能给我们带来对程序行为的有效见解,但对于困难问题来说,这种方式就显得笨拙且耗时了。 你也可能需要更加深入地理解程序,仅依靠打印日志做不到。此时…...

【已解决】No Python at ‘D:\Python\python.exe‘
起因,我把我的python解释器,重新移了个位置,导致我在Pycharm中的爬虫项目启动,结果出现这个问题。 然后,从网上查到了这篇博客: 【已解决】No Python at ‘D:\Python\python.exe‘-CSDN博客 但是,按照上述…...

蓝桥杯双周赛算法心得——数树数(dfs)
大家好,我是晴天学长,一个简单的dfs思想,需要的小伙伴可以关注支持一下哦!后续会继续更新的。 1) .数树数 2) .算法思路 代码的主要逻辑是: 1.使用Scanner读取输入的整数n和q,其中n表示测试用例的数量&am…...
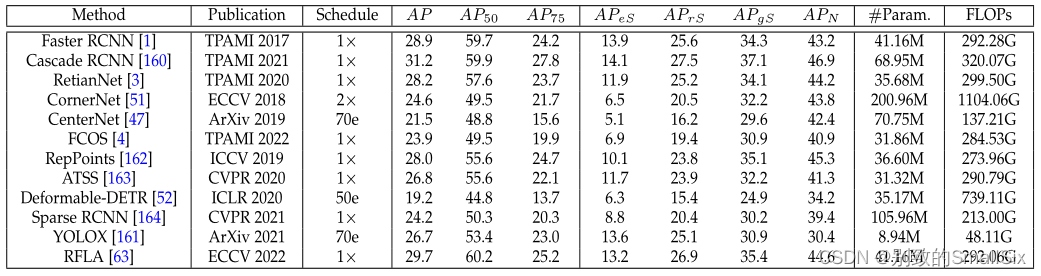
综述:大规模小目标检测
论文地址: Towards Large-Scale Small Object Detection: Survey and Benchmarksarxiv.org/abs/2207.14096 目录 摘要 1.Introduction 1.1 与之前综述的比较 1.2 总结 2.小目标检测回顾 2.1 问题定义 2.2 主要挑战 2.3 小目标检测算法回顾 3.小目标检测的数据集 …...

ORACLE XXX序列 goes below MINVALUE 无法实例化的处理办法
--序列增加区分 --删除未使用序列表 DECLARE V_CNT INT; BEGINSELECT COUNT(*) INTO V_CNT FROM USER_SEQUENCES WHERE SEQUENCE_NAME SEQ_INTELLECT_BIZ_DETAIL_ID;IF V_CNT1 THEN BEGINEXECUTE IMMEDIATE DROP SEQUENCE SEQ_INTELLECT_BIZ_DETAIL_ID;END;END IF; END; / ---…...

6款流程图制作软件:一站式指南
流程图是一种常用的图示工具,可以帮助我们更清晰地表达和展示流程、流程图等内容。在今天已经变得非常普及和便捷,接下来本文将于大家分享6款好用的流程图软件,一起来看看吧! 博思白板boardmix 博思白板boardmix是一款基于浏览器…...
)
第三章:Python中的序列(上)
Python中的序列 是一种有序的数据结构,通常用于存储一组相关的元素。Python中的序列包括列表(list)、元组(tuple)和字符串(string)。 1. 列表 是最常用的序列类型,它是可变的(即可以添加、删除和修改元素)。列表中的元素可以是任何类型,包括其他列表或元组。列表…...
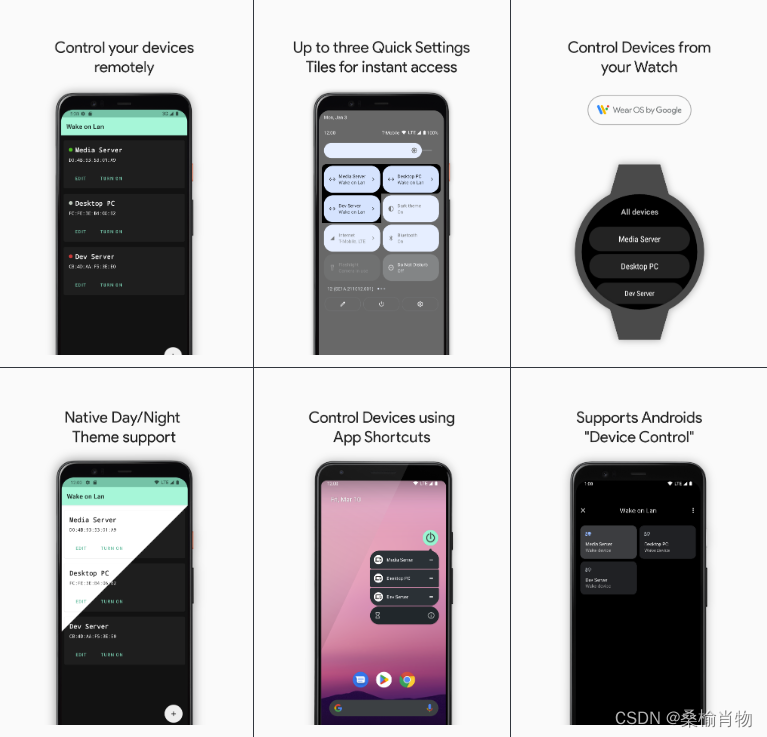
使用.NET实现WOL唤醒远程开机
文章目录 1. 背景2. 关于 WOL2.1 WOL 工作原理2.2 开启网卡唤醒功能 3. 快速验证3.1 局域网 Wake on Lan 应用3.2 Ubuntu 的 etherwake 命令4. 代码实现4.1 创建.NET控制台应用程序4.2 编写代码4.3 运行应用程序 5. 最后 1. 背景 家居自动化是现代智能家居的重要组成部分&…...

适用于 Golang 的任务调度程序 AGScheduler
以前一直使用 Python 的任务调度库 APScheduler(支持任务持久化,支持多种存储方式),但由于没有找到和它功能和使用方式类似的 Golang 库,所以模仿 APScheduler 3.x 写了个简易版本的 AGScheduler。 AGScheduler Advan…...
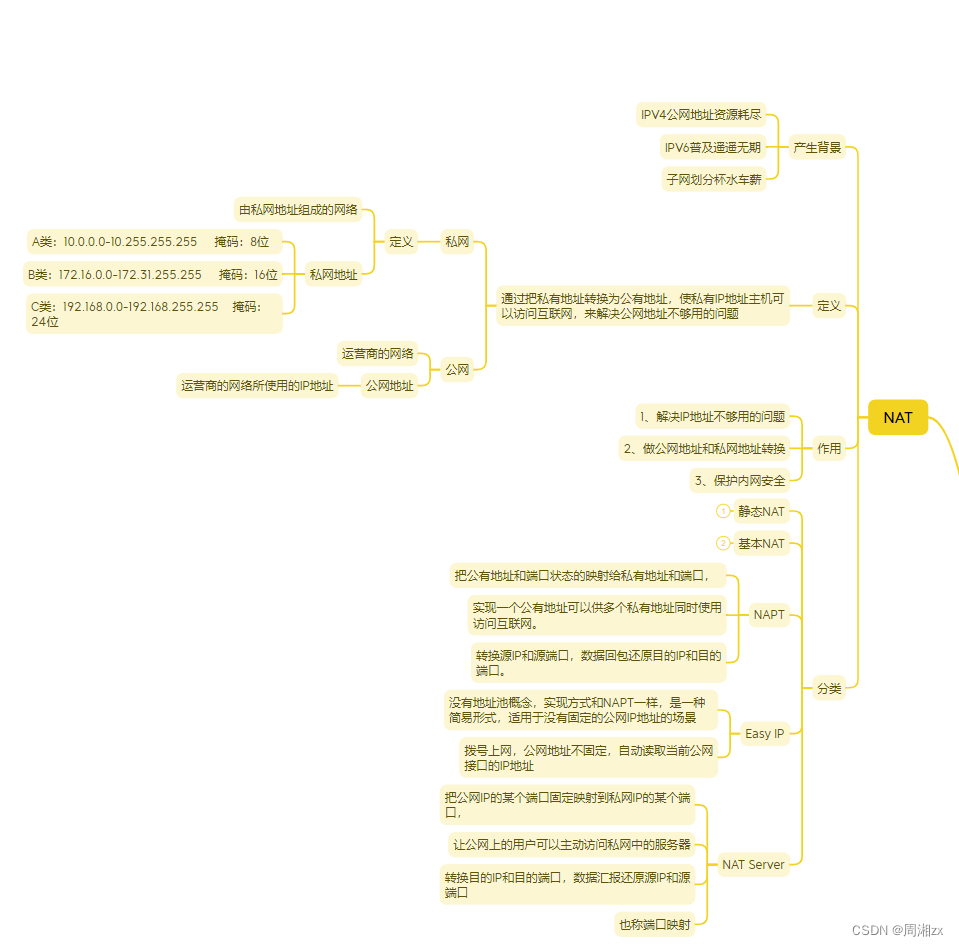
【HCIP】HCIA复习
目录 大纲 情景代入 访问百度/谷歌服务器的准备工作 1、计算机网络发展第一阶段人机交互的加工过程 2、OSI参考模型 3、TCP/IP参考模型 访问谷歌(百度)服务器的流程 1、主机需要一个IP地址才能上网(本场景中通过DHCP服务获取IP地址&a…...
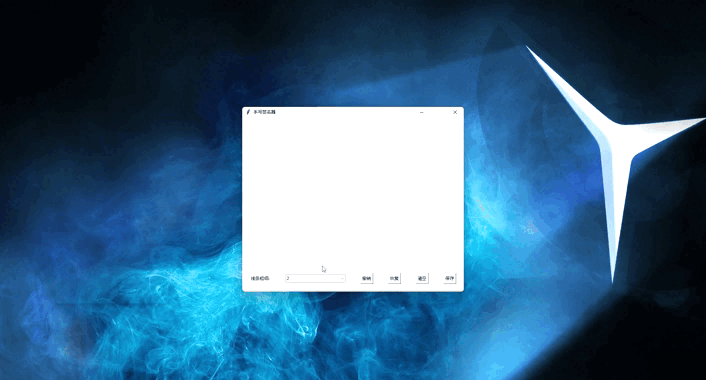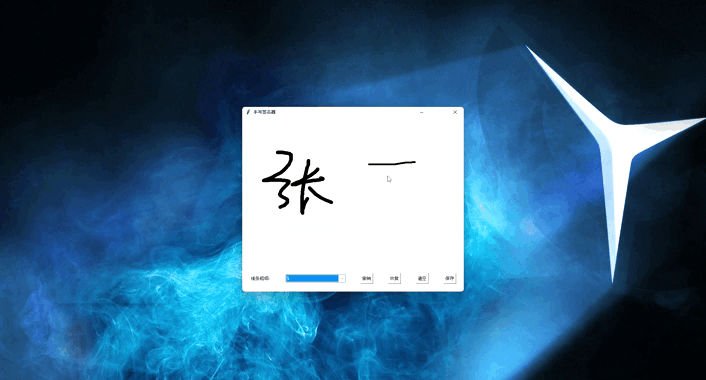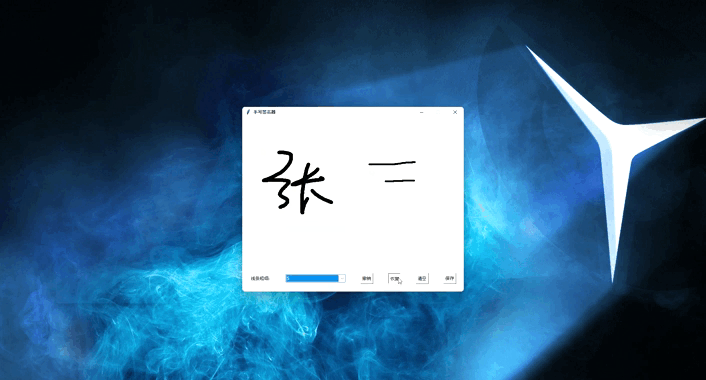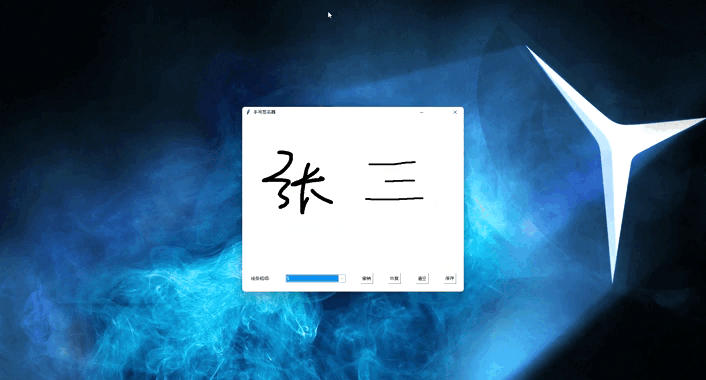
【Python小项目之Tkinter应用】【实用工具】实现手写签名器,可选线条粗细,支持清空、撤销、恢复功能,可将写好的签名保存成图片
文章目录 前言一、实现思路二、关键代码三、完整代码总结同系列项目文章:前言 老规矩,先看效果: 在手写签名窗口中,用户可以选择线条粗细来签名,点击清空按钮可以清空画布,点击撤销按钮可以撤销一笔,点击恢复按钮可以撤销上一步进行的清空或撤销操作,点击保存按钮可以…...

Jenkins集成newman
一、Docker环境准备 二、Jenkins环境准备 三、登录Jenkins 安装NodeJs插件 四、Jenkins全局工具配置Nodejs 五、创建Jenkins自由风格项目 构建步骤1:选择Execute NodeJS script构建步骤2:选择执行shell脚本 六、将postman相关的脚本、环境变量数据、全局…...

Excel——对其他工作表和工作簿的引用
一、引用其他sheet页表区域 若希望在公式中引用其他工作表的单元格区域,可以在公式编辑状态下,通过鼠标单击相应的工作表标签,然后选择相应的单元格区域。 例1 跨sheet页引用其他工作表区域 如图1所示的工作表Sheet2为工资表。 在Sheet1表…...

如何正确的防止服务器被攻击?103.216.153.x
网站服务器被攻击是新建网站常常发生的事情,对于新手来说这也是非常棘手的问题。那么一旦遇到这样的情况,我们需要如何解决呢?怎么才能防止服务器被攻击,怎么保障自己网站信息的安全,如果发现被攻击又该怎么做呢&#…...

本地生活将成快手新的营收增长点
监制 | 何玺 排版 | 叶媛 快手本地生活开始强化B端市场。 据了解,快手 “本地商家”APP已经正式上线。这是快手为本地生活商家推出的独立工作平台,有助于商家提升经营效率。 新APP的上线,标志着快手本地生活业务布局,正从过去侧…...

信息化工程测试验收管理制度
1、总则 1.1、目的 为规范XXXXX单位的信息系统建设和工程项目测试验收准则,特制订本管理制度。 1.2、范围 本制度适用于XXXXX单位工程测试验收管理。 1.3、职责 信息系统建设和其他信息系统工程类项目的测试和验收主要由项目负责人负责,必要的时候…...

解决vue2设置cross-env设置环境变量不起作用问题
1. 配置package.json package.json的scripts里增加打包脚本 "build-app": "cross-env VUE_APP_LOGIN_VALUEapp NODE_OPTIONS--max_old_space_size4096 node build/build.js",2.配置webpack.prod.conf.js webpack.prod.conf.js的plugins里增加脚本 new …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
