正交实验与极差分析

正交试验极差分析流程如下图：

1. 正交试验说明
   正交试验是研究多因素试验的设计方法。对于多因素、多水平的实验要求，如果每个因素的每个水平都要进行试验，这样就会耗费大量的人力和时间，正交试验可以选择出具有代表性的少数试验进行试验，从而找出最优试验方案。
   例如进行一个三因素三水平的试验，按照全面试验的思想，就要进行=27次实验，实验次数多且重复；但是如果选择进行正交试验就只需要做9次试验，大大节省了人力物力和时间，因此正交试验在很多领域都被广泛应用。
2. 正交表设计

正交试验是通过现成的规格化表——正交表，科学的安排试验并通过极差分析或者方差分析来分析试验结果，找到最优试验方案的。

正交表是正交试验的基本工具，以正交表为例说明下正交表的概念和特点。式中L表示正交表，数字 3 表示因素的水平个数，右上指数为 4，标明最多可安排因素(包括交互)的个数。L右下的 9 表示本正交试验总的试验次数。即如采用该试验，那么可以完成安排最多4 个因素，每个因素最多 3个水平的总共9次的试验。

当前有一份三因素三水平的数据需要进行正交试验，目的是得到最优试验组合。

首先进行正交表的设计。设计正交表，可以使用SPSSAU进行，分析路径【SPSSAU->实验/医学研究->正交试验】。有时候可能会遇到SPSSAU输出的正交表的因素或水平数与预期不一致，是因为SPSSAU系统默认找到最接近的标准正交表，如果不一致，需要进行正交表的改造，例如使用拟水平法、组合法、并列法等。

具体操作可以查看SPSSAU帮助手册进行了解学习。https://spssau.com/helps/medicalmethod/orthogonal.html

本案例使用SPSSAU得到三因素三水平正交设计表如下：

得到正交设计表后，接下来需要按照正交表进行试验。

三、进行试验

从得到正交表可以看出，本次试验共需要进行9次。试验1为使用因子1的1水平、因子2的1水平和因子3的1水平进行试验；试验2为使用因子1的1水平、因子2的2水平和因子3的3水平进行试验，以此类推，分别得到9次试验的分析结果。

本次试验的三个因子分别是A、B、C，三个因子各有三个水平简单记为水平123，得到最终试验结果如下：

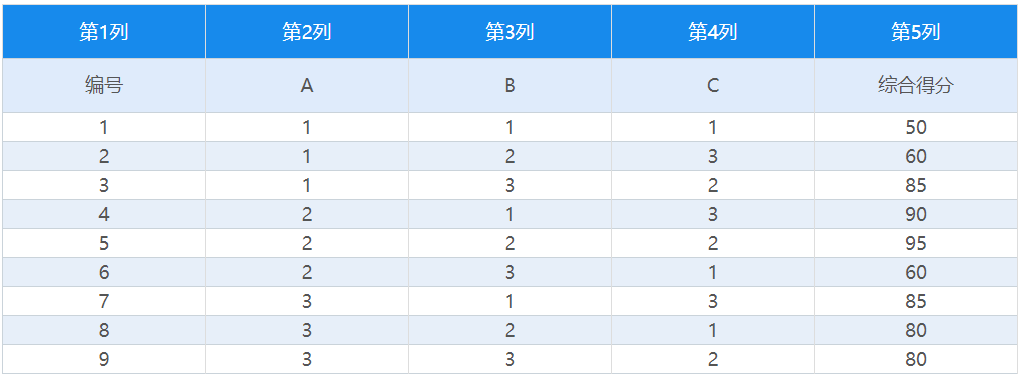
得到试验结果之后，对实验数据进行分析，目的是找到试验的最优因素和最优试验组合，即希望找到ABC三个因子中哪一个对综合得分的影响最优，同时找到综合得分最高的因素水平组合。

四、极差分析

对正交试验数据进行分析主要有两种分析方法，分别是极差分析与方差分析。极差分析又称直观分析法，它具有计算简单、直观形象、简单易懂等优点，是正交试验结果分析最常用的方法。本案例使用极差分析法进行分析。

极差分析设计的相关指标机器说明，如下表所示：

使用SPSSAU进行极差分析，操作如下图，需要注意的是，SPSSAU默认情况下试验数据越大越好，如果试验数据越小越好，此时可下拉选择‘试验数据类型’参数为‘越小越好’即可。

极差分析输出两类结果，分别是极差分析表格和因子各水平均值图。接下来进行极差分析结果解读，确定最优因素和最佳因素水平组合。

五、结果解读

结果1：极差分析表格

首先看R值（因素极差值）：R值的大小反映了各因素对于试验结果的影响程度大小。所以本次试验结果显示，C因素为最优因素，对试验结果影响最大，其次是A因素，最后是B因素。因而三个因素的优劣排列顺序为因子C>因子A>因子B。

再看最佳水平：最佳水平显示，因子A在水平3的时候最优；因子B在水平2的时候最优；因子3在水平2的时候最优。

综合上述分析，得到这次试验的最优因素是“因子C”，最佳因素水平组合是“因子A的3水平、因子B的2水平、因子C的2水平”。

结果2：因子各水平均值图

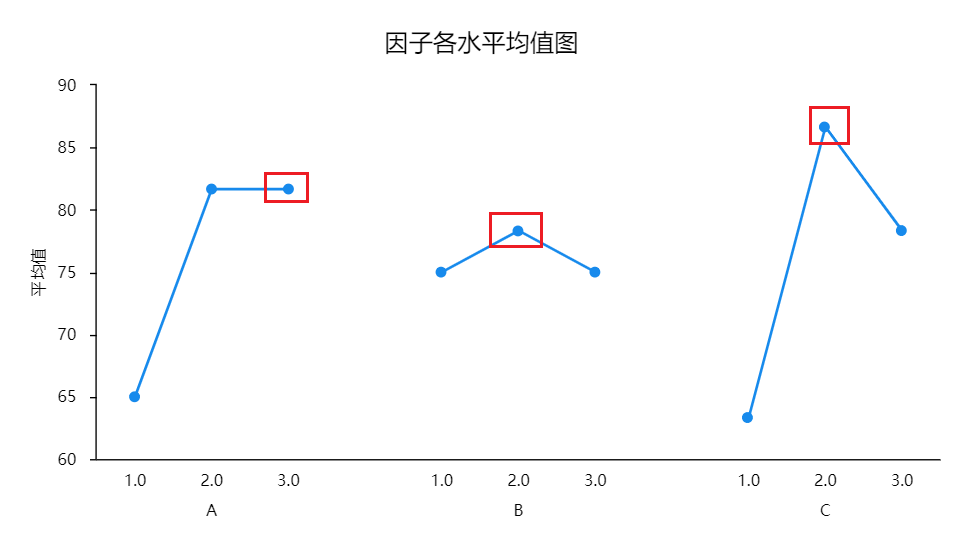
因素各水平均值图展示各个因素各个水平的试验数据平均值情况；可通过图形直观查看各水平的试验数据平均值情况并进行对比；并找出最佳水平组合，进行分析汇总。从上图也可以直观看出最佳因素水平组合为“因子A的3水平、因子B的2水平、因子C的2水平”。

六、总结

进行正交试验分析，首先需要进行正交表的设计， SPSSAU默认找到最接近的标准正交表，如果与试验预期不符，可以进行正交表的改造后再使用。然后根据得到的正交表进行试验，记录好试验结果，上传到SPSSAU系统。最后使用极差分析（或方差分析）来分析正交试验结果，得到最优因素和最佳因素水平组合。