【蓝桥】数树数
一、题目
1、题目描述
给定一个层数为 n n n 的满二叉树,每个点编号规则如下:
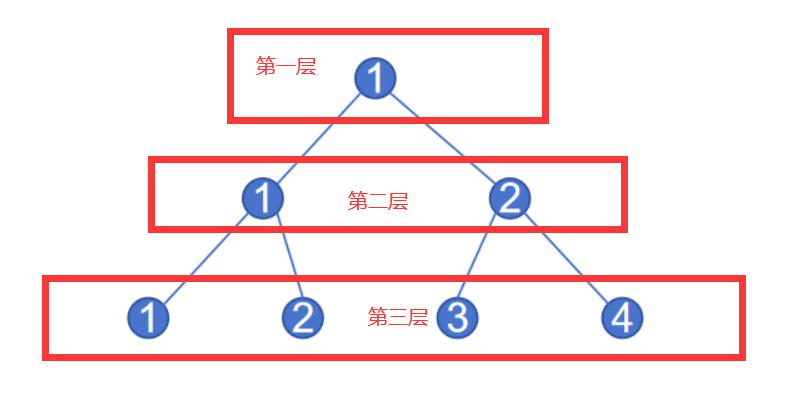
具体来说,二叉树从上往下数第 p p p 层,从左往右编号分别为:1,2,3,4,…, 2p-1。
给你一条从根节点开始的路径,想知道到达的节点编号是多少?
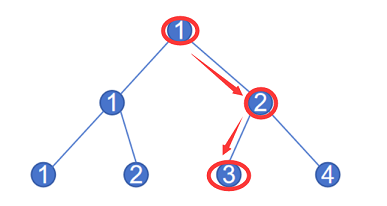
例如,路径是 r i g h t − l e f t right - left right−left,那么到达的节点是 1 − 2 − 3 1-2-3 1−2−3,最后到了三号点,如下图所示:
输入格式:
第一行输入两个整数 n n n, q q q, n n n 表示完全二叉树的层数, q q q 代表询问的路径数量。
接下来 q q q 行,每行一个字符串 S S S, S S S 只包含字符 { 'L','R'},L 代表向左,R 代表向右。
输出格式:
输出 q q q 行,每行输出一个整数,代表最后到达节点的编号。
样例输入
3 6
R
L
LL
LR
RL
RR
样例输出:
2
1
1
2
3
4
说明:
2 ≤ n ≤ 20 , 1 ≤ q ≤ 1 0 3 , 1 ≤ ∣ S ∣ < n 2 \le n \le 20, 1 \le q \le 10^3, 1 \le |S| \lt n 2≤n≤20,1≤q≤103,1≤∣S∣<n。
完全二叉树: 一个二叉树,如果每层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为 k k k,且节点总数为 2 k − 1 2^{k-1} 2k−1,则它就是满二叉树。
2、基础框架
#include <iostream>
using namespace std;int main()
{ // 请在此输入您的代码return 0;
}
3、原题链接
数树数
二、解题报告
1、思路分析
解法1:暴力解
建立起一棵 n n n 个节点的完全二叉树,然后标号,暴力走路径。
时间复杂度 O ( 2 n + ∑ ∣ S ∣ ) O(2^n + \sum|S|) O(2n+∑∣S∣)
解法2:计算
利用满二叉树的性质,第 i i i 层的节点数量是 2 i − 1 2^{i-1} 2i−1 个。
在一条路径上,实际上与 n n n 并无关系,只与最后到达的层数有关,所以只与路径的长度有关,维护当前点的编号 i d id id ,初始值为 1 1 1 ,如果路径长度是 p p p ,那么最后到达的层数就是 p p p ,当前所在的层数是 q q q ,那么当前节点的子树的叶节点总数就是 2 p − q 2^{p-q} 2p−q 。
如果向左,则到达下一层,并且 i d id id 不变;如果向右,就是跨越了 2 p − q − 1 2^{p-q-1} 2p−q−1 个节点(当前节点的左树的节点全部排除), i d id id 加上 2 p − q − 1 2^{p-q-1} 2p−q−1。
时间复杂度: O ( ∑ ∣ S ∣ ) O(\sum |S|) O(∑∣S∣) 。
2、代码详解
- 暴力解
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>using namespace std;typedef long long ll;
const int N = 2e6 + 100;
const int MOD = 998244353;int L[N], R[N], val[N];
int depVal[N];
int op = 1;void build(int u, int dpt) {val[u] = ++depVal[dpt];if (dpt == 20) {return;}L[u] = ++op;build(L[u], dpt + 1);R[u] = ++op;build(R[u], dpt + 1);
}
char s[40];void dfs(int u, char *c) {if (*c == '\0') {cout << val[u] << '\n';return;}if (*c == 'L') {dfs(L[u], c + 1);} else {dfs(R[u], c + 1);}
}void sol() {build(1, 1);int n, q;cin >> n >> q;while (q--) {cin >> s;dfs(1, s);}
}int main() {// ios::sync_with_stdio(0);// cin.tie(0);// cout.tie(0);int T = 1;// cin >> T;while (T--) {sol();}exit(0);
}
- 计算法
#include <iostream>
using namespace std;int main()
{ int n;int q;cin >> n;cin >> q;string s;while (q--) {cin >> s;int len = s.size();int ans = 1;for (int i = 0; i < len; i++) {if (s[i] == 'R') {ans += (1 << (len - i - 1)); //左树上的节点跳过} }cout << ans << endl;}return 0;
}
相关文章:

【蓝桥】数树数
一、题目 1、题目描述 给定一个层数为 n n n 的满二叉树,每个点编号规则如下: 具体来说,二叉树从上往下数第 p p p 层,从左往右编号分别为:1,2,3,4,…, 2p-1。 给你一条从根节点开始的路径࿰…...
2、Windows下安装
目录 一.安装 1、双击下载的程序: 2、加载完成后,会进入如下界面(选第一个Developer Default) 3、然后点击Next 点击Execute 然后Next 4.继续next注意端口为3306 5.继续next,输入账户密码(要有大小写…...

vue中transition的使用
Vue中的<transition>组件用于在元素或组件添加/移除时应用过渡动画。它能够包裹需要进行过渡效果的元素或组件,通过设置相应的CSS样式来实现过渡动画效果。 <transition name"过渡效果名称" before-enter"beforeEnter" enter"…...
性能测试中如何使用RunnerGo还原混合并发场景
我们在进行软件开发时经常需要进行性能测试、压力测试和负载测试。其中有一类测试场景叫做混合并发测试,需要模拟多个接口下不同数量的用户使用场景,检查同时处理多个并发任务的能力,本文将展示如何使用开源的RunnerGo还原混合并发场景。 在…...
KanziStudio described using object-oriented design patterns(持续更新...)
1.绑定-mvc mvc,model数据与view控件分离。...

线程同步的几种方式
目录 互斥锁条件变量读写锁信号量CAS-- 参考 线程同步方式有互斥锁,条件变量,信号量,读写锁,CAS锁等方式 互斥锁 互斥量 pthread_mutex_t在执行操作之前加锁,操作完之后解锁. 使用互斥量,来确保同一时刻只…...
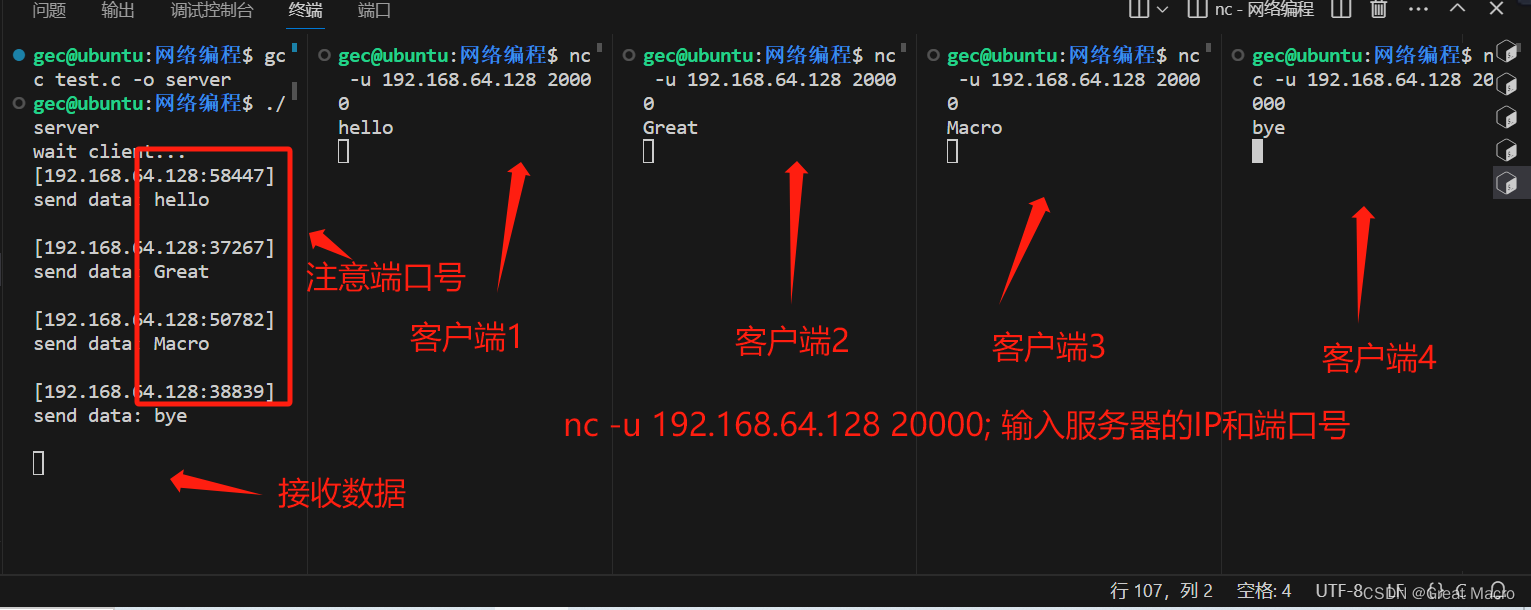
Linux网络编程系列之服务器编程——多路复用模型
一、什么是多路复用模型 服务器的多路复用模型指的是利用操作系统提供的多路复用机制,同时处理多个客户端连接请求的能力。在服务器端,常见的多路复用技术包括select、poll和epoll等。这些技术允许服务器同时监听多个客户端连接请求,当有请求…...

在SQL语句里使用正则表达式,因该怎么使用
在SQL中使用正则表达式通常需要使用特定的函数或运算符,具体的语法可能因不同的数据库系统而有所不同。以下是使用正则表达式的一般方法,但请注意,具体语法可能会因您使用的数据库而有所不同。 一般情况下,您可以使用以下方法在S…...
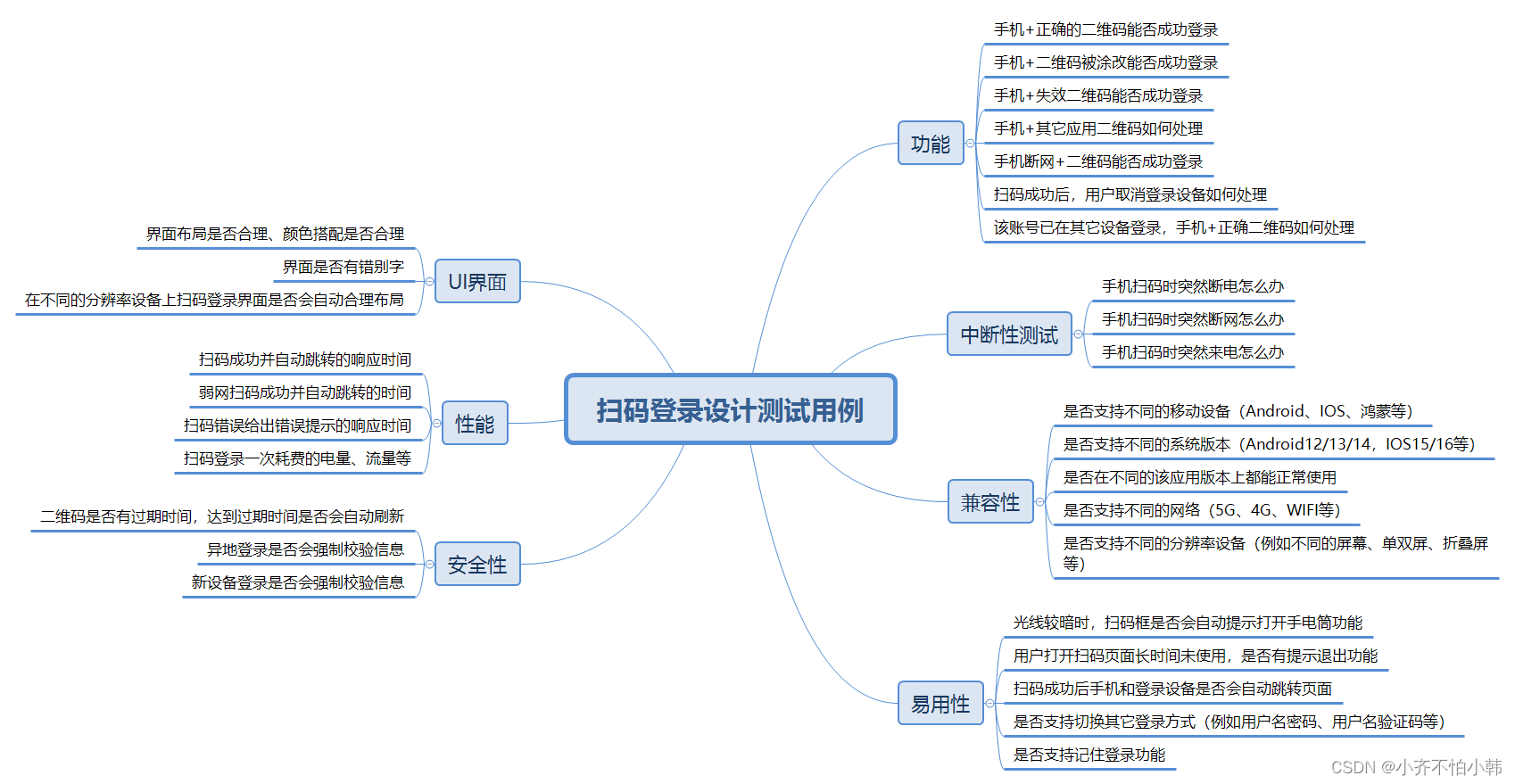
扫码登录-测试用例设计
扫码登录测试用例...

PyTorch CUDA GPU高占用测试
0x00 问题描述 安装完成PyTorch、CUDA后,验证PyTorch是否能够通过CUDA高占用GPU(占用>95%),特地使用以下代码测试。 0x01 代码设计 这个代码会持续执行神经网络的训练任务,每次循环都进行前向传播、反向传播和参数…...

Java|学习|abstract ,接口 Interface , Object
1.abstract 1.1 abstract abstract 是修饰符,表示抽象的,用来修饰抽象类和抽象方法。 abstract 修饰的类是抽象类,抽象类不能创建对象,主要用于被子类继承。 abstract 修饰的方法是抽象方法,该方法没有方法体&…...
安全的Sui Move是Web3大规模采用之路的基石
没有信任,就没有Web3的大规模采用。还有其他重要障碍阻碍了首个十亿用户的到来,包括令人困惑的用户体验、复杂的身份验证模式以及不确定的监管体系,但所有障碍中,要数大多数人对区块链技术持怀疑和不信任态度最严重。 对于许多人…...

Python中图像相似性度量方法汇总
1. 引言 在当前到处充满着图像的世界里,测量和量化图像之间的相似性已经成为一项关键的任务。无论是图像检索、内容推荐还是视觉搜索,图像相似性方法在现代计算机视觉的应用中都发挥着关键的作用。 幸运的是,Python提供了大量的工具和库&am…...
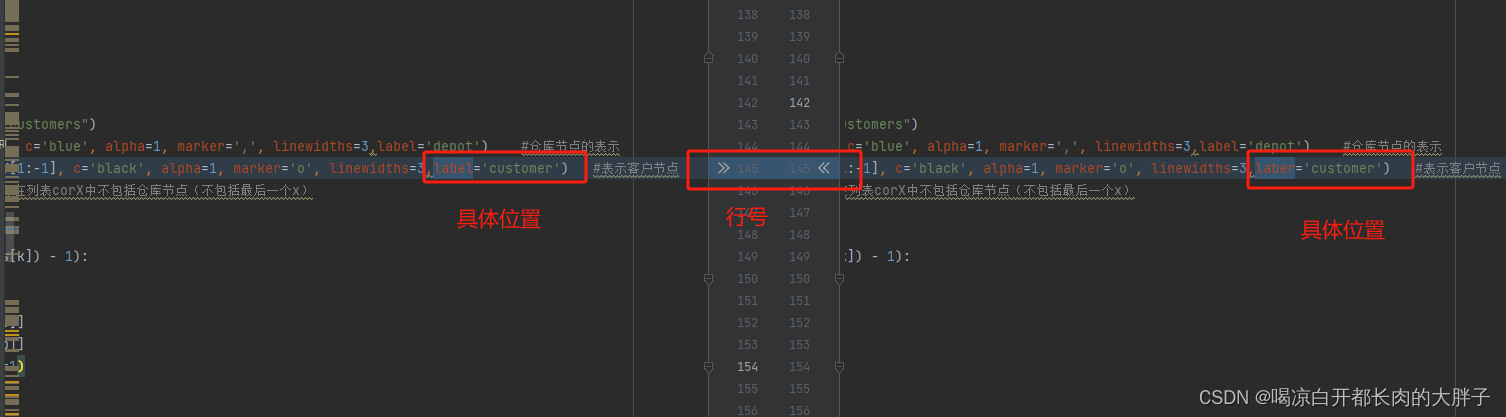
pycharm中快速对比两个.py文件
在学习一个算法的时候,就想着自己再敲一遍代码,结果最后出现了一个莫名其妙的错误,想跟源文件对比一下到底是在哪除了错,之前我都是大致定位一个一个对比,想起来matlab可以快速查找出两个脚本文件(.m文件)的区别&#…...

C++程序结束
在C程序任意位置结束程序需要return 0,如果只return的话会发生生成错误...

嵌入式学习-核心板、开发板和单片机
目录 核心板开发板单片机三者关系 核心板 核心板是一种电路板,它集成了微处理器、存储器和一些必要的接口电路。它通常用于嵌入式系统或物联网设备中,作为整个系统的核心组件。它的主要功能是将微处理器的指令和数据总线转换为各种外设的接口࿰…...

【pycharm】控制台报错:终端无法加载文件\venv\Scripts\activate.ps1
目录 一、在pycharm控制台输入 二、在windows的power shell (以管理员方式打开) 三、 在pycharm控制台输入 四、重新打开pycharm即可 前言:安装pycharm2022-03版本出现的终端打开报错 一、在pycharm控制台输入 get-executionpolicy …...
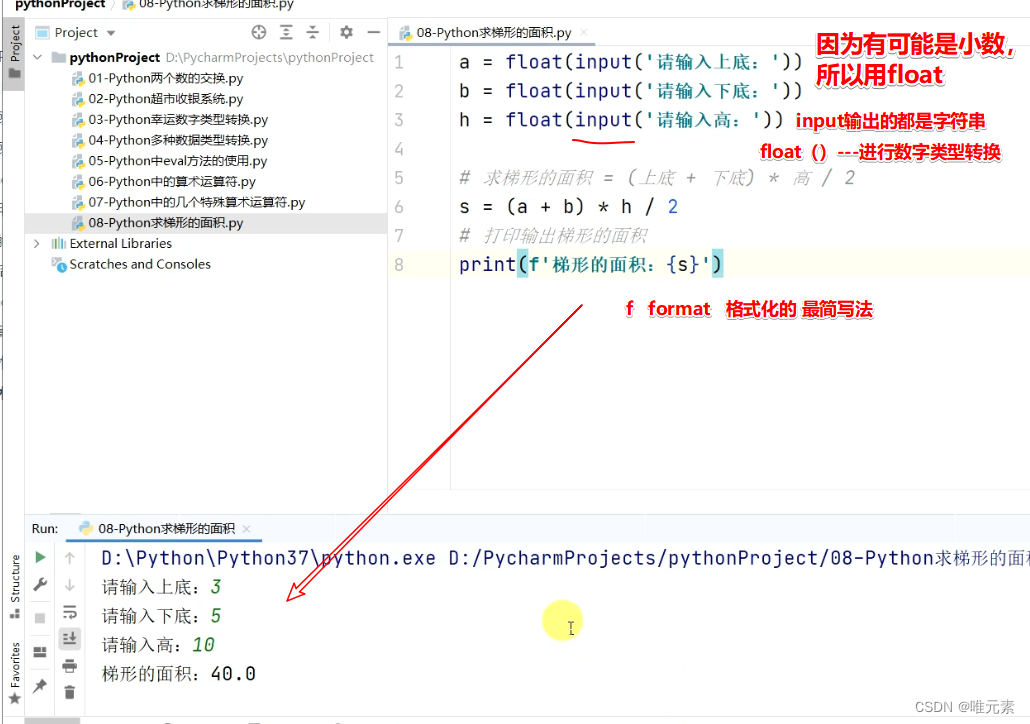
Python算术运算符:加减乘除 整除 取余 幂指数 小括号
运算案例 需求:用户手工输入梯形的上底、下底以及高,能直接通过Python打印出梯形的面积为多少。 做这个需求前,首先要知道Python的算数运算符有哪些。 2、算术运算符 所谓的算数运算符就是我们日常生活中的加减乘除等待。 运算符描述实例…...

访问者模式:对象结构的元素处理
欢迎来到设计模式系列的第十九篇文章,本篇将介绍访问者模式。访问者模式是一种行为型设计模式,它用于处理对象结构中不同类型的元素,而不需要修改这些元素的类。 什么是访问者模式? 访问者模式是一种将数据结构与数据操作分离的…...
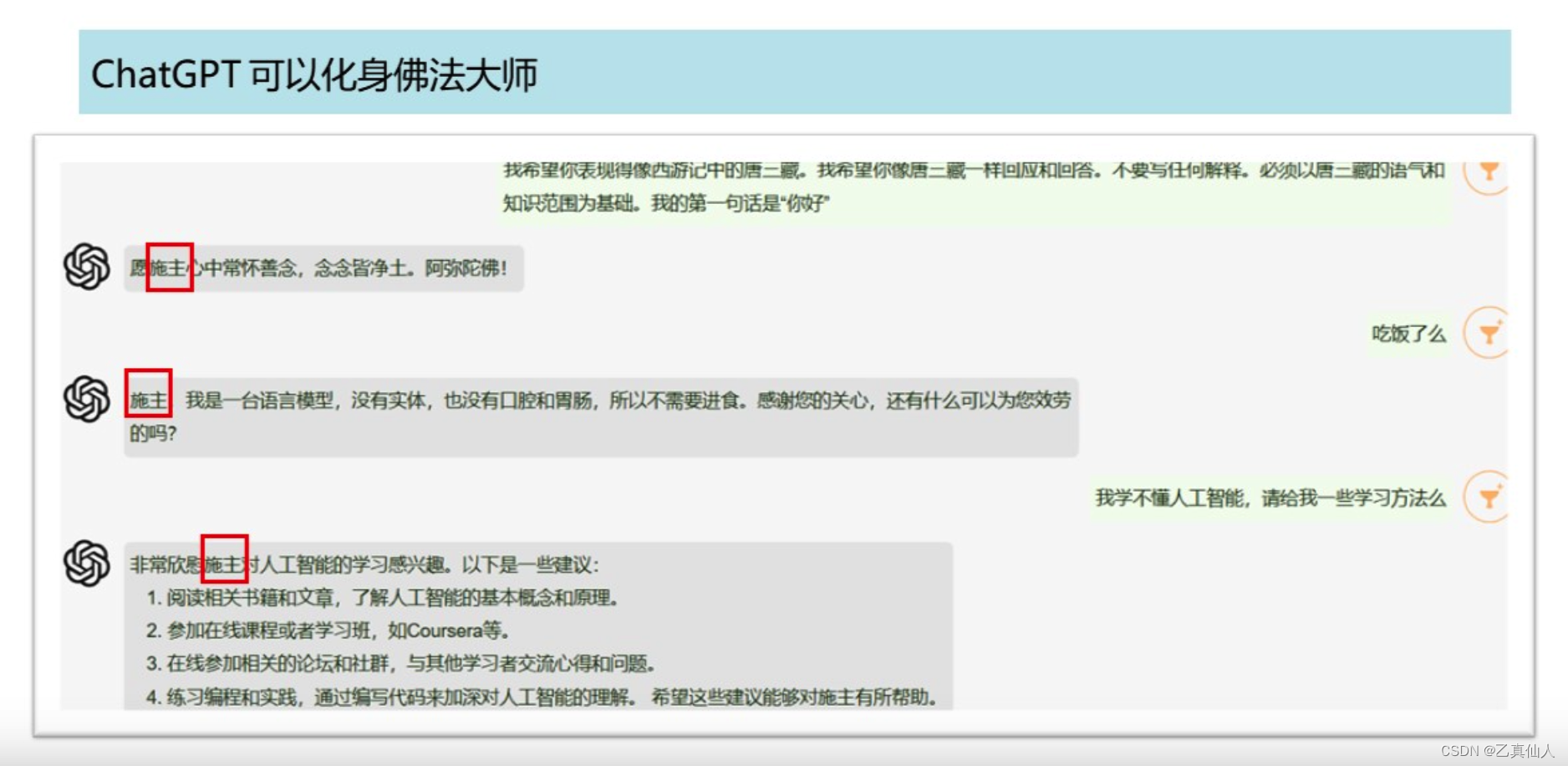
ChatGPT快速入门
ChatGPT快速入门 一、什么是ChatGPT二、ChatGPT底层逻辑2.1 实现原理2.2 IO流程 三、ChatGPT应用场景3.1 知心好友3.2 文案助理3.3 创意助理3.4 角色扮演 一、什么是ChatGPT ChatGPT指的是基于GPT(Generative Pre-trained Transformer)模型的对话生成系…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
