十个面试排序算法
一、 前言
最常考的是快速排序和归并排序,并且经常有面试官要求现场写出这两种排序的代码。对这两种排序的代码一定要信手拈来才行。还有插入排序、冒泡排序、堆排序、基数排序、桶排序等。面试官对于这些排序可能会要求比较各自的优劣、各种算法的思想及其使用场景。还有要会分析算法的时间和空间复杂度。
二、排序算法
2.1 冒泡算法
大体思想就是通过与相邻元素的比较和交换来把小的数交换到最前面。类似于水泡向上升一样,因此而得名。举个栗子,对5,3,8,6,4这个无序序列进行冒泡排序。首先从后向前冒泡,4和6比较,把4交换到前面,序列变成5,3,8,4,6。同理4和8交换,变成5,3,4,8,6,3和4无需交换。5和3交换,变成3,5,4,8,6,3.这样一次冒泡就完了,把最小的数3排到最前面了。对剩下的序列依次冒泡就会得到一个有序序列。冒泡排序的时间复杂度为O(n^2)。
import java.util.Arrays;public class Test {public static void BubbleSort(int[] arr) {if (arr == null || arr.length <= 0) {return;}for (int i = 0; i < arr.length - 1; i++) {for (int j = arr.length - 1; j > i; j--) {if (arr[j] < arr[j - 1]) {swap(arr, j - 1, j);}}}}private static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}public static void main(String[] args) {int[] array = {0, 31, 12, 2, 8};// 执行冒泡排序BubbleSort(array);Arrays.stream(array).forEach(System.out::println);}}
2.2 选择排序
选择排序的思想其实和冒泡排序有点类似,都是在一次排序后把最小的元素放到最前面。但是过程不同,冒泡排序是通过相邻的比较和交换。而选择排序是通过对整体的选择。举个栗子,对5,3,8,6,4这个无序序列进行简单选择排序,首先要选择5以外的最小数来和5交换,也就是选择3和5交换,一次排序后就变成了3,5,8,6,4.对剩下的序列一次进行选择和交换,最终就会得到一个有序序列。其实选择排序可以看成冒泡排序的优化,因为其目的相同,只是选择排序只有在确定了最小数的前提下才进行交换,大大减少了交换的次数。选择排序的时间复杂度为O(n^2)
import java.util.Arrays;public class Test {public static void SelectSort(int[] arr) {if (arr == null || arr.length <= 0) {return;}int minIndex = 0;for (int i = 0; i < arr.length - 1; i++) {minIndex = i;for (int j = i + 1; j < arr.length; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}if (minIndex != i) {swap(arr, i, minIndex);}}}private static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}public static void main(String[] args) {int[] array = {0, 31, 12, 2, 8};SelectSort(array);Arrays.stream(array).forEach(System.out::println);}}
2.3 插入算法
插入排序不是通过交换位置而是通过比较找到合适的位置插入元素来达到排序的目的的。相信大家都有过打扑克牌的经历,特别是牌数较大的。在分牌时可能要整理自己的牌,牌多的时候怎么整理呢?就是拿到一张牌,找到一个合适的位置插入。这个原理其实和插入排序是一样的。举个栗子,对5,3,8,6,4这个无序序列进行简单插入排序,首先假设第一个数的位置时正确的,想一下在拿到第一张牌的时候,没必要整理。然后3要插到5前面,把5后移一位,变成3,5,8,6,4.想一下整理牌的时候应该也是这样吧。然后8不用动,6插在8前面,8后移一位,4插在5前面,从5开始都向后移一位。注意在插入一个数的时候要保证这个数前面的数已经有序。简单插入排序的时间复杂度也是O(n^2)。
import java.util.Arrays;public class Test {public static void InsertSort(int[] arr) {if (arr == null || arr.length <= 0) {return;}for (int i = 1; i < arr.length; i++) {int j = i;int target = arr[i];while (j >0 && target <arr[j-1]) {arr[j]=arr[j-1];j --;}arr[j] = target;}}public static void main(String[] args) {int[] array = {0, 31, 12, 2, 8};InsertSort(array);Arrays.stream(array).forEach(System.out::println);}}
2.4 快速算法
实际应用当中快速排序确实也是表现最好的排序算法。冒泡排序虽然高端,但其实其思想是来自冒泡排序,冒泡排序是通过相邻元素的比较和交换把最小的冒泡到最顶端,而快速排序是比较和交换小数和大数,这样一来不仅把小数冒泡到上面同时也把大数沉到下面。
举个栗子:对5,3,8,6,4这个无序序列进行快速排序,思路是右指针找比基准数小的,左指针找比基准数大的,交换之。
5,3,8,6,4 用5作为比较的基准,最终会把5小的移动到5的左边,比5大的移动到5的右边。
5,3,8,6,4 首先设置i,j两个指针分别指向两端,j指针先扫描(思考一下为什么?)4比5小停止。然后i扫描,8比5大停止。交换i,j位置。
5,3,4,6,8 然后j指针再扫描,这时j扫描4时两指针相遇。停止。然后交换4和基准数。
4,3,5,6,8 一次划分后达到了左边比5小,右边比5大的目的。之后对左右子序列递归排序,最终得到有序序列。
上面留下来了一个问题为什么一定要j指针先动呢?首先这也不是绝对的,这取决于基准数的位置,因为在最后两个指针相遇的时候,要交换基准数到相遇的位置。一般选取第一个数作为基准数,那么就是在左边,所以最后相遇的数要和基准数交换,那么相遇的数一定要比基准数小。所以j指针先移动才能先找到比基准数小的数。
快速排序是不稳定的,其时间平均时间复杂度是O(nlgn)。
import java.util.Arrays;public class Test {public static int partition(int[]arr , int left , int right) {int pKey = arr[left];int pPointer = left;while (left < right) {while (left <right && arr[right] >= pKey) {right --;}while (left < right && arr[left] <= pKey) {left ++;}swap(arr, left, right);}swap(arr, pPointer, left);return left;}public static void QuickSort(int[] arr, int left, int right){if (left >= right || arr == null || arr.length <=0) {return;}int mid = partition(arr, left, right);QuickSort(arr, left, mid - 1);QuickSort(arr,mid +1, right);}private static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}public static void main(String[] args) {int[] array = {0, 31, 12, 2, 8};QuickSort(array, 0,array.length-1);Arrays.stream(array).forEach(System.out::println);}}
总结快速排序的思想:冒泡+二分+递归分治
2.5 堆排序
堆排序是借助堆来实现的选择排序,思想同简单的选择排序,以下以大顶堆为例。注意:如果想升序排序就使用大顶堆,反之使用小顶堆。原因是堆顶元素需要交换到序列尾部。
首先,实现堆排序需要解决两个问题:
1. 如何由一个无序序列键成一个堆?
2. 如何在输出堆顶元素之后,调整剩余元素成为一个新的堆?
第一个问题,可以直接使用线性数组来表示一个堆,由初始的无序序列建成一个堆就需要自底向上从第一个非叶元素开始挨个调整成一个堆。
第二个问题,怎么调整成堆?首先是将堆顶元素和最后一个元素交换。然后比较当前堆顶元素的左右孩子节点,因为除了当前的堆顶元素,左右孩子堆均满足条件,这时需要选择当前堆顶元素与左右孩子节点的较大者(大顶堆)交换,直至叶子节点。我们称这个自堆顶自叶子的调整成为筛选。
从一个无序序列建堆的过程就是一个反复筛选的过程。若将此序列看成是一个完全二叉树,则最后一个非终端节点是n/2取底个元素,由此筛选即可。
import java.util.Arrays;public class Test {public static void AdjustHeap(int[]arr , int start , int end) {int temp = arr[start];for (int i = 2 * start + 1; i <= end; i *= 2) {if (i < end && arr[i] < arr[i + 1]){i++;}if (temp > arr[i]) {break;}arr[start] = arr[i];start = i;}arr[start] = temp;}public static void HeapSort(int[]arr) {if ( arr == null || arr.length <=0) {return;}for (int i = arr.length/2; i>=0 ; i--) {AdjustHeap(arr, i, arr.length-1);}for (int i = arr.length-1; i >=0 ; i--) {swap(arr, 0, i);AdjustHeap(arr, 0, i-1);}}private static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}public static void main(String[] args) {int[] array = {0, 31, 12, 2, 8};HeapSort(array );Arrays.stream(array).forEach(System.out::println);}}
2.6 希尔排序
希尔排序是插入排序的一种高效率的实现,也叫缩小增量排序。简单的插入排序中,如果待排序列是正序时,时间复杂度是O(n),如果序列是基本有序的,使用直接插入排序效率就非常高。希尔排序就利用了这个特点。基本思想是:先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录基本有序时再对全体记录进行一次直接插入排序。
import java.util.Arrays;public class Test {public static void shellInsert(int[] arr, int d) {for (int i = d; i < arr.length; i++) {int j = i - d;int temp = arr[i];while (j >= 0 && arr[j] > temp) {arr[j + d] = arr[j];j = j - d;}if (j != i - d) {arr[j + d] = temp;}}}public static void ShellSort(int[] arr) {if (arr == null || arr.length <= 0) {return;}int d = arr.length / 2;while (d >= 1) {shellInsert(arr, d);d = d / 2;}}private static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}public static void main(String[] args) {int[] array = {0, 31, 12, 2, 8};ShellSort(array);Arrays.stream(array).forEach(System.out::println);}}
2.7 归并排序
归并排序是另一种不同的排序方法,因为归并排序使用了递归分治的思想,所以理解起来比较容易。其基本思想是,先递归划分子问题,然后合并结果。把待排序列看成由两个有序的子序列,然后合并两个子序列,然后把子序列看成由两个有序序列。。。。。倒着来看,其实就是先两两合并,然后四四合并。。。最终形成有序序列。空间复杂度为O(n),时间复杂度为O(nlogn)。
2.8 计数排序
虽然前面基于比较的排序的下限是O(nlogn)。但是确实也有线性时间复杂度的排序,只不过有前提条件,就是待排序的数要满足一定的范围的整数,而且计数排序需要比较多的辅助空间。其基本思想是,用待排序的数作为计数数组的下标,统计每个数字的个数。然后依次输出即可得到有序序列。
2.9 桶排序
假设有一组长度为N的待排关键字序列K[1....n]。首先将这个序列划分成M个的子区间(桶) 。然后基于某种映射函数 ,将待排序列的关键字k映射到第i个桶中(即桶数组B的下标 i) ,那么该关键字k就作为B[i]中的元素(每个桶B[i]都是一组大小为N/M的序列)。接着对每个桶B[i]中的所有元素进行比较排序(可以使用快排)。然后依次枚举输出B[0]….B[M]中的全部内容即是一个有序序列。bindex=f(key) 其中,bindex 为桶数组B的下标(即第bindex个桶), k为待排序列的关键字。桶排序之所以能够高效,其关键在于这个映射函数,它必须做到:如果关键字k1<k2,那么f(k1)<=f(k2)。也就是说B(i)中的最小数据都要大于B(i-1)中最大数据。很显然,映射函数的确定与数据本身的特点有很大的关系。
2.10 基数排序
基数排序又是一种和前面排序方式不同的排序方式,基数排序不需要进行记录关键字之间的比较。基数排序是一种借助多关键字排序思想对单逻辑关键字进行排序的方法。所谓的多关键字排序就是有多个优先级不同的关键字。比如说成绩的排序,如果两个人总分相同,则语文高的排在前面,语文成绩也相同则数学高的排在前面。。。如果对数字进行排序,那么个位、十位、百位就是不同优先级的关键字,如果要进行升序排序,那么个位、十位、百位优先级一次增加。基数排序是通过多次的收分配和收集来实现的,关键字优先级低的先进行分配和收集。
三、总结
冒泡排序、选择排序、插入排序三种简单的排序及其变种快速排序、堆排序、希尔排序三种比较高效的排序。后面我们又分析了基于分治递归思想的归并排序还有计数排序、桶排序、基数排序三种线性排序。我们可以知道排序算法要么简单有效,要么是利用简单排序的特点加以改进,要么是以空间换取时间在特定情况下的高效排序。但是这些排序方法都不是固定不变的,需要结合具体的需求和场景来选择甚至组合使用。才能达到高效稳定的目的。没有最好的排序,只有最适合的排序。
下面就总结一下排序算法的各自的使用场景和适用场合。
| 排序方法 | 平均时间 | 最坏时间 | 辅助存储 |
|---|---|---|---|
| 简单排序 | |||
| 快速排序 | |||
| 堆排序 | |||
| 归并排序 | |||
| 基数排序 |
1. 从平均时间来看,快速排序是效率最高的,但快速排序在最坏情况下的时间性能不如堆排序和归并排序。而后者相比较的结果是,在n较大时归并排序使用时间较少,但使用辅助空间较多。
2. 上面说的简单排序包括除希尔排序之外的所有冒泡排序、插入排序、简单选择排序。其中直接插入排序最简单,但序列基本有序或者n较小时,直接插入排序是好的方法,因此常将它和其他的排序方法,如快速排序、归并排序等结合在一起使用。
3. 基数排序的时间复杂度也可以写成O(d*n)。因此它最使用于n值很大而关键字较小的的序列。若关键字也很大,而序列中大多数记录的最高关键字均不同,则亦可先按最高关键字不同,将序列分成若干小的子序列,而后进行直接插入排序。
4. 从方法的稳定性来比较,基数排序是稳定的内排方法,所有时间复杂度为O(n^2)的简单排序也是稳定的。但是快速排序、堆排序、希尔排序等时间性能较好的排序方法都是不稳定的。稳定性需要根据具体需求选择。
5. 上面的算法实现大多数是使用线性存储结构,像插入排序这种算法用链表实现更好,省去了移动元素的时间。具体的存储结构在具体的实现版本中也是不同的。
相关文章:
十个面试排序算法
一、 前言 最常考的是快速排序和归并排序,并且经常有面试官要求现场写出这两种排序的代码。对这两种排序的代码一定要信手拈来才行。还有插入排序、冒泡排序、堆排序、基数排序、桶排序等。面试官对于这些排序可能会要求比较各自的优劣、各种算法的思想及其使用场景…...
技术学习群-第四期内容共享
本期是技术群聊的第四期。还是那句话,《群聊免费进入》。一起来看看本期分享内容。 uiautomator-Error问题 在使用u2的过程中,有时候需要使用到uiautomator这个工具来进行查阅层级。但是博主遇到了这么个问题。 《问题分析》:发生此问题的原因…...

冒泡排序/鸡尾酒排序
冒泡排序 冒泡排序(Bubble Sort)是一种简单的排序算法,它通过多次交换相邻元素的位置来实现排序。它的基本思想是从数组的第一个元素开始,比较相邻的两个元素,如果它们的顺序错误,则交换它们的位置。重复进…...

代码随想录算法训练营第五十三天|309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费
代码随想录算法训练营第五十三天|309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费 309.最佳买卖股票时机含冷冻期714.买卖股票的最佳时机含手续费 309.最佳买卖股票时机含冷冻期 题目链接:309.最佳买卖股票时机含冷冻期 文章链接 状态:有…...
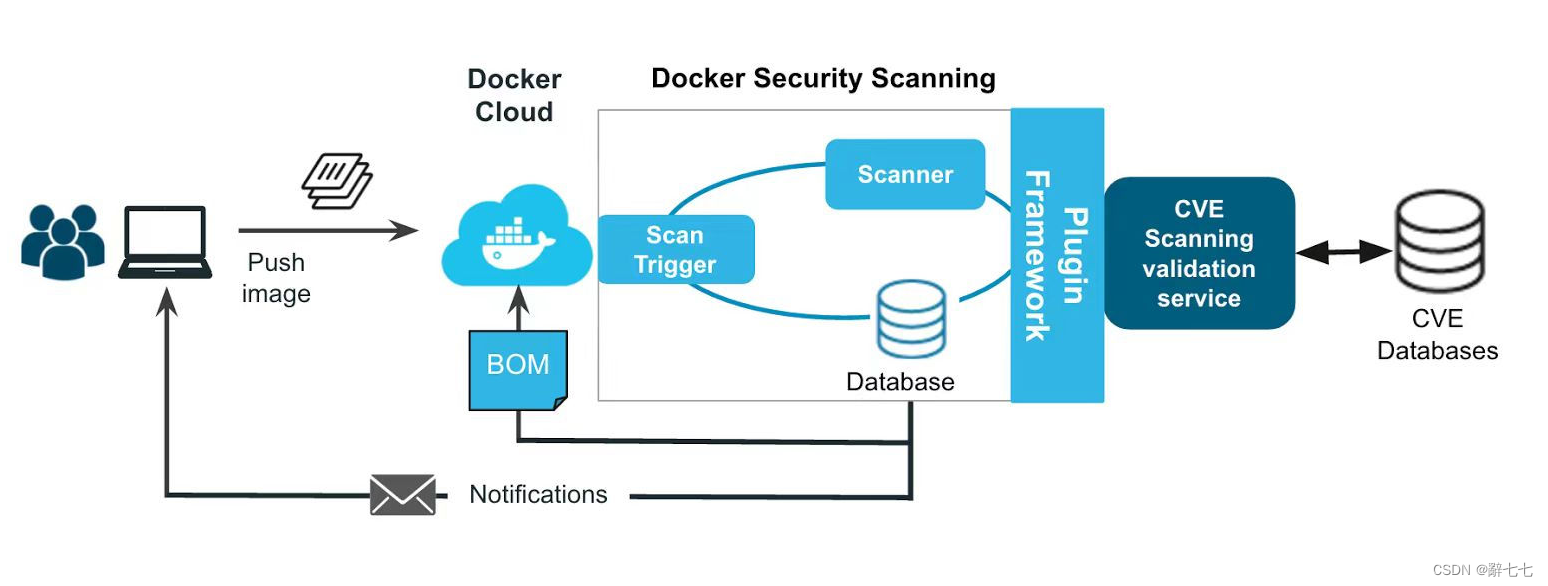
【Docker】Docker的使用案例以及未来发展、Docker Hub 服务、环境安全、容器部署安全
作者简介: 辭七七,目前大二,正在学习C/C,Java,Python等 作者主页: 七七的个人主页 文章收录专栏: 七七的闲谈 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!💖…...

qt qtabwidget获取当前选项卡的所有按键
要获取当前选项卡中的所有按键,可以通过以下步骤进行: 通过currentIndex()函数获取当前选项卡的索引。 使用widget()函数获取当前选项卡的QWidget。 连接QWidget的keyPressEvent事件,并在事件处理函数中获取按下的按键信息。 下面是示例代…...
为什么Excel插入图片不显示,点击能够显示
很久没有Excel了,今天在做Excel表格时,发现上传图片后不能显示,但是点击还是能够出现图片的 点击如下 点击能看到,但是不显示? 最后发现只需鼠标右键点击浮动即可显示...
使用Python创建faker实例生成csv大数据测试文件并导入Hive数仓
文章目录 一、Python生成数据1.1 代码说明1.2 代码参考 二、数据迁移2.1 从本机上传至服务器2.2 检查源数据格式2.3 检查大小并上传至HDFS 三、beeline建表3.1 创建测试表并导入测试数据3.2 建表显示内容 四、csv文件首行列名的处理4.1 创建新的表4.2 将旧表过滤首行插入新表 一…...

qml基础语法
文章目录 基础语法例子 属性例子 核心元素元素item RectangleText例子 Image例子 MouseArea例子Component(组件)例子简单变换例子 定位器ColumnRowGridFlowRepeater 布局InputKeys 基础语法 QML是一种用于描述对象如何相互关联的声明式语言。 QtQuick是…...
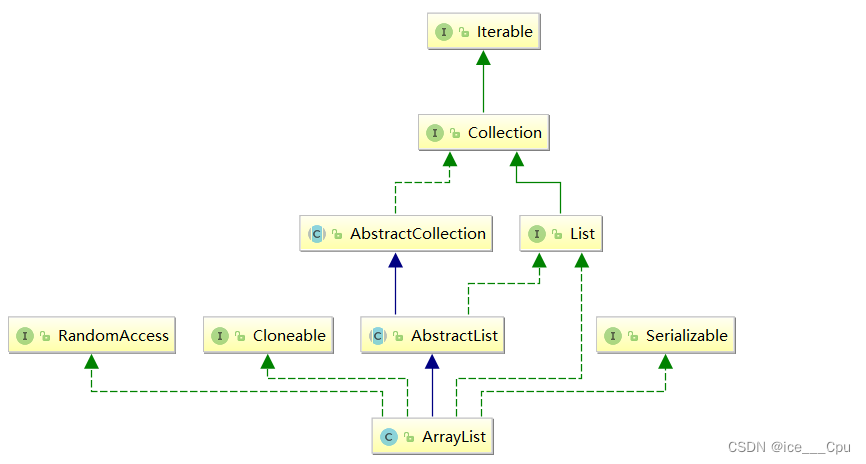
数据结构 - 2(顺序表10000字详解)
一:List 1.1 什么是List 在集合框架中,List是一个接口,继承自Collection。 Collection也是一个接口,该接口中规范了后序容器中常用的一些方法,具体如下所示: Iterable也是一个接口,Iterabl…...

05在IDEA中配置Maven的基本信息
配置Maven信息 配置Maven家目录 每次创建Project工程后都需要设置Maven家目录位置,否则IDEA将使用内置的Maven核心程序和使用默认的本地仓库位置 一般我们配置了Maven家目录后IDEA就会自动识别到conf/settings.xml配置文件和配置文件指定的本地仓库位置创建新的P…...
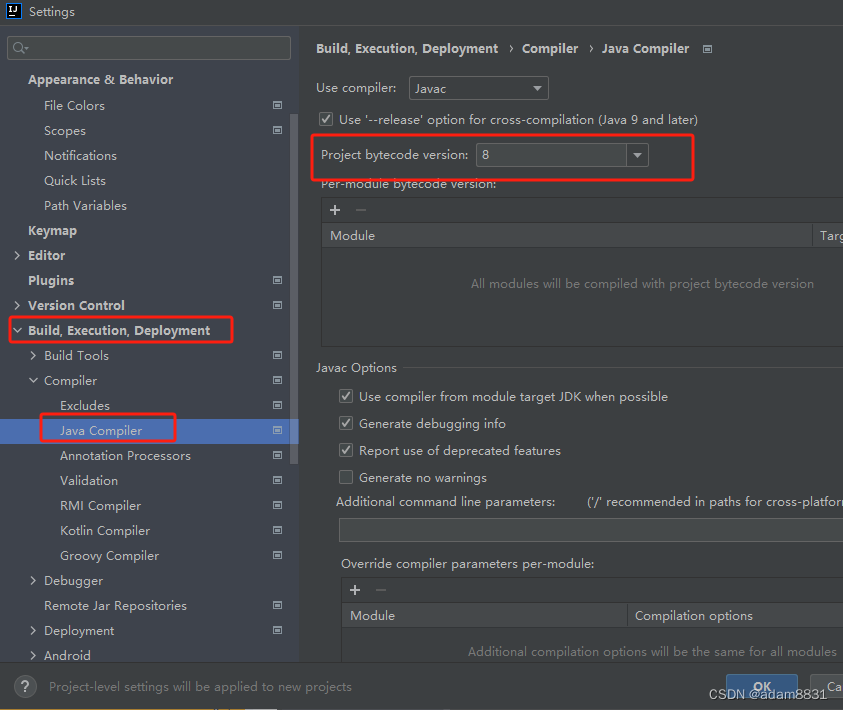
基于IDEA 配置Maven环境和JDK版本(全局)
1.首先启动IDEA,进去初始界面 选择 Customize 之后,选择 All settings 2. 选择下图中的列表配置 3. 找到Maven下的Runner, 配置JRE的版本,选择自己下载使用的jdk的版本即可 4.最后配置Compiler 下的 Java Compiler 选择自己的jdk版本号&am…...

mysql数据库 windows迁移至linux
1.打开navicat,选择一个数据库进行操作: 之后文件会保存为一个xxx.sql文件,之后打开xftp,把生成的sql放进一个文件夹中(/home/dell/linuxmysql): 之后登录mysql数据库,并创建一个新的数据库,然后…...

P4491 [HAOI2018] 染色
传送门:洛谷 解题思路: 写本题需要知道一个前置知识: 假设恰好选 k k k个条件的方案数为 f ( k ) f(k) f(k);先钦定选 k k k个条件,其他条件无所谓的方案数为 g ( k ) g(k) g(k) 那么存在这样的一个关系: g ( k ) ∑ i k n C i k f ( i ) g(k)\sum_{ik}^nC_{i}^kf(i) g(k)…...
)
12096 - The SetStack Computer (UVA)
题目链接如下: Online Judge 这道题我一开始的思路大方向其实是对的,但细节怎么实现set到int的哈希没能想清楚(没想到这都能用map)。用set<string>的做法来做,测试数据小的话答案是对的,但大数据时…...

Pygame中将鼠标形状设置为图片2-1
在Pygame中利用Sprite类的派生类将鼠标形状设置为图片,其原理就是将Sprite类的派生类对应图片的位置设置为鼠标的当前位置即可。其效果如图1所示。 图1 将鼠标设置为图片 从图1可以看出,鼠标的形状变为红色的,该红色的随着鼠标的移动而移动&…...

Vue3 + Nodejs 实战 ,文件上传项目--实现图片上传
目录 技术栈 1. 项目搭建前期工作(不算太详细) 前端 后端 2.配置基本的路由和静态页面 3.完成图片上传的页面(imageUp) 静态页面搭建 上传图片的接口 js逻辑 4.编写上传图片的接口 5.测试效果 结语 博客主页:専心_前端,javascript,mys…...
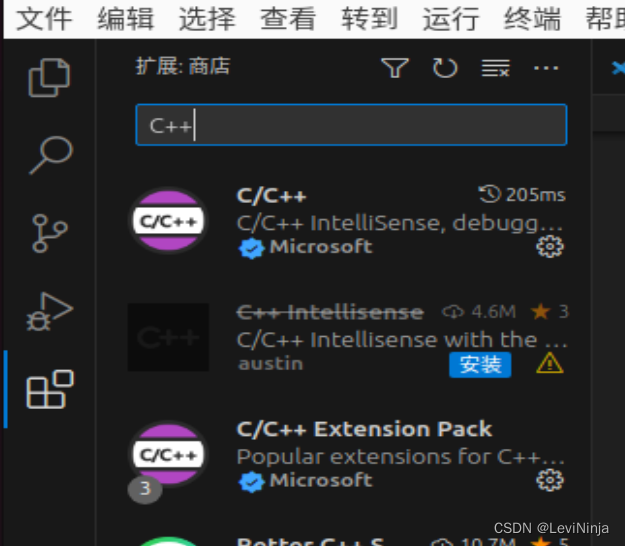
linux C++ vscode连接mysql
1.linux使用Ubuntu 2.Ubuntu安装vscode 2.1 安装的是snap版本,直接打开命令行执行 sudo snap install --classic code 3.vscode配置C 3.1 直接在扩展中搜索C安装即可 我安装了C, Chinese, code runner, 安装都是同理 4.安装mysql sudo apt update sudo apt install mysql-…...
[资源推荐]langchain、LLM相关
之前很多次逛github或者去B站看东西或者说各种浏览资讯的情况,都会先看两眼然后收藏然后就吃灰的情况,那既然这样,不如多看几眼,看看是否真的能用得上,能用在哪,然后用几句话总结出来,分享出来&…...

hdfs笔记
1.HDFS shell 1.0查看帮助 hadoop fs -help <cmd> 1.1上传 hadoop fs -put <linux上文件> <hdfs上的路径> 1.2查看文件内容 hadoop fs -cat <hdfs上的路径> 1.3查看文件列表 hadoop fs -ls / 1.4…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
