P4491 [HAOI2018] 染色
传送门:洛谷
解题思路:
写本题需要知道一个前置知识:
假设恰好选 k k k个条件的方案数为 f ( k ) f(k) f(k);先钦定选 k k k个条件,其他条件无所谓的方案数为 g ( k ) g(k) g(k)
那么存在这样的一个关系: g ( k ) = ∑ i = k n C i k f ( i ) g(k)=\sum_{i=k}^nC_{i}^kf(i) g(k)=∑i=knCikf(i)
上述式子的含义是可以枚举实际上选了几个,然后再这 i i i个中选择 k k k个作为钦定的计算方案数.因为钦定这种方式是存在重复方案的
然后使用二项式反演可以实现钦定和恰好之间的转化.
经过二项式反演可以得到: f ( k ) = ∑ i = k n C i k ∗ ( − 1 ) i − k ∗ g ( i ) f(k)=\sum_{i=k}^nC_{i}^{k}*(-1)^{i-k}*g(i) f(k)=∑i=knCik∗(−1)i−k∗g(i).
对于本题来说,我们的 g ( i ) g(i) g(i)其实很容易写出.设 g ( i ) g(i) g(i)为恰好出现 i i i个的出现次数为 s s s的颜色的方案数.不难写出 g ( i ) = C m i A n s ∗ i ( s ∗ i ) ! ∗ ( m − i ) n − s ∗ i g(i)=C_m^i\frac{A_n^{s*i}}{(s*i)!}*(m-i)^{n-s*i} g(i)=Cmi(s∗i)!Ans∗i∗(m−i)n−s∗i
然后我们反演一下就得到了: f ( k ) = ∑ i = k n C i k ( − 1 ) i − k g ( i ) f(k)=\sum_{i=k}^{n}C_{i}^{k}(-1)^{i-k}g(i) f(k)=i=k∑nCik(−1)i−kg(i)
稍微化解一下就能得到:
f ( k ) ∗ k ! = ∑ i = k n g ( i ) ∗ i ! ∗ ( − 1 ) i − k ( i − k ) ! f(k)*k!=\sum_{i=k}^ng(i)*i!*\frac{(-1)^{i-k}}{(i-k)!} f(k)∗k!=i=k∑ng(i)∗i!∗(i−k)!(−1)i−k
然后我们设 G ( i ) = g ( i ) ∗ i ! , H ( i ) = ( − 1 ) i − k ( i − k ) ! G(i)=g(i)*i!,H(i)=\frac{(-1)^{i-k}}{(i-k)!} G(i)=g(i)∗i!,H(i)=(i−k)!(−1)i−k就能得到 F ( k ) = ∑ i = k n G ( i ) ∗ H ( i − k ) F(k)=\sum_{i=k}^nG(i)*H(i-k) F(k)=i=k∑nG(i)∗H(i−k)
我们使用经典套路将 G G G数组 r e v e r s e reverse reverse一下,就得到了 F ( K ) = ∑ i = k n G ( n − i ) ∗ H ( i − k ) F(K)=\sum_{i=k}^nG(n-i)*H(i-k) F(K)=i=k∑nG(n−i)∗H(i−k)
PS:需要注意的是此时翻转的n可以不为n,不熟悉的人可能会搞不清楚
然后这是一道很显然的卷积式子.此时我们使用 N T T NTT NTT卷一下即可.此时我们的的 f ( k ) f(k) f(k)就是卷积完之后第 n − k n-k n−k项的系数.
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
inline void print(__int128 x){if(x<0) {putchar('-');x=-x;}if(x>9) print(x/10);putchar(x%10+'0');
}
#define maxn 10001000
#define int long long
const int mod=1004535809;
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int qpow(int a,int b) {int ans=1;while(b) {if(b&1) ans=ans*a%mod;b>>=1;a=a*a%mod;}return ans;
}
int rev[maxn];
void NTT(int *a,int n,int inv) {for(int i=0;i<=n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);for(int len=1;len<=(n>>1);len<<=1) {int gn=qpow(inv==1?3:qpow(3,mod-2),(mod-1)/(len<<1));for(int i=0;i<=n;i+=(len<<1)) {int g0=1;for(int j=0;j<=len-1;j++) {int x=a[i+j],y=a[i+j+len]*g0%mod;a[i+j]=(x+y)%mod;a[i+j+len]=((x-y)%mod+mod)%mod;g0=g0*gn%mod;}}}
}
int fac[maxn],in_fac[maxn];
void init(int limit) {fac[0]=1;for(int i=1;i<=limit;i++) {fac[i]=fac[i-1]*i%mod;}in_fac[limit]=qpow(fac[limit],mod-2);for(int i=limit-1;i>=0;i--) {in_fac[i]=in_fac[i+1]*(i+1)%mod;}
}
int C(int a,int b) {return fac[a]*in_fac[b]%mod*in_fac[a-b]%mod;
}
int A(int a,int b) {return fac[a]*in_fac[a-b]%mod;
}
int w[maxn];int g[maxn];int G[maxn],H[maxn];int F[maxn];
signed main() {int n=read();int m=read();int s=read();init(max(n,m));for(int i=0;i<=m;i++) {w[i]=read();}int k=min(m,n/s);for(int i=0;i<=k;i++) {g[i]=C(m,i)*A(n,s*i)%mod*qpow(in_fac[s],i)%mod*qpow(m-i,n-s*i)%mod;}for(int i=0;i<=k;i++) {G[i]=g[i]*fac[i]%mod;H[i]=((i&1?-1:1)*in_fac[i]%mod+mod)%mod;}reverse(G,G+k+1);int limit=1,len=0;while(limit<=k+k) limit<<=1,len++;for(int i=0;i<=limit;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(len-1));NTT(G,limit,1);NTT(H,limit,1);for(int i=0;i<=limit;i++) F[i]=G[i]*H[i]%mod;NTT(F,limit,-1);int inv=qpow(limit,mod-2);for(int i=0;i<=limit;i++) {F[i]=F[i]*inv%mod;}int ans=0;for(int i=0;i<=k;i++) {ans=(ans+F[k-i]*in_fac[i]%mod*w[i]%mod)%mod;}cout<<ans<<endl;return 0;
}
相关文章:

P4491 [HAOI2018] 染色
传送门:洛谷 解题思路: 写本题需要知道一个前置知识: 假设恰好选 k k k个条件的方案数为 f ( k ) f(k) f(k);先钦定选 k k k个条件,其他条件无所谓的方案数为 g ( k ) g(k) g(k) 那么存在这样的一个关系: g ( k ) ∑ i k n C i k f ( i ) g(k)\sum_{ik}^nC_{i}^kf(i) g(k)…...
)
12096 - The SetStack Computer (UVA)
题目链接如下: Online Judge 这道题我一开始的思路大方向其实是对的,但细节怎么实现set到int的哈希没能想清楚(没想到这都能用map)。用set<string>的做法来做,测试数据小的话答案是对的,但大数据时…...

Pygame中将鼠标形状设置为图片2-1
在Pygame中利用Sprite类的派生类将鼠标形状设置为图片,其原理就是将Sprite类的派生类对应图片的位置设置为鼠标的当前位置即可。其效果如图1所示。 图1 将鼠标设置为图片 从图1可以看出,鼠标的形状变为红色的,该红色的随着鼠标的移动而移动&…...

Vue3 + Nodejs 实战 ,文件上传项目--实现图片上传
目录 技术栈 1. 项目搭建前期工作(不算太详细) 前端 后端 2.配置基本的路由和静态页面 3.完成图片上传的页面(imageUp) 静态页面搭建 上传图片的接口 js逻辑 4.编写上传图片的接口 5.测试效果 结语 博客主页:専心_前端,javascript,mys…...
linux C++ vscode连接mysql
1.linux使用Ubuntu 2.Ubuntu安装vscode 2.1 安装的是snap版本,直接打开命令行执行 sudo snap install --classic code 3.vscode配置C 3.1 直接在扩展中搜索C安装即可 我安装了C, Chinese, code runner, 安装都是同理 4.安装mysql sudo apt update sudo apt install mysql-…...
[资源推荐]langchain、LLM相关
之前很多次逛github或者去B站看东西或者说各种浏览资讯的情况,都会先看两眼然后收藏然后就吃灰的情况,那既然这样,不如多看几眼,看看是否真的能用得上,能用在哪,然后用几句话总结出来,分享出来&…...

hdfs笔记
1.HDFS shell 1.0查看帮助 hadoop fs -help <cmd> 1.1上传 hadoop fs -put <linux上文件> <hdfs上的路径> 1.2查看文件内容 hadoop fs -cat <hdfs上的路径> 1.3查看文件列表 hadoop fs -ls / 1.4…...

java_方法引用和构造器引用
文章目录 一、方法引用1.1、方法引用的理解1.2、格式1.3、举例 二、构造器引用2.1、格式2.2、例子2.3、数组引用 一、方法引用 1.1、方法引用的理解 方法引用,可以看做是基于lambda表达式的进一步刻画当需要提供一个函数式接口的实例时,可以使用lambda…...

Flink Log4j 2.x使用Filter过滤日志类型
Flink Log4j 2.x使用Filter过滤日志类型(区别INFO、ERROR) 文章目录 Flink Log4j 2.x使用Filter过滤日志类型(区别INFO、ERROR)ThresholdFilterLevelMatchFilter 日志级别: ALL < TRACE < DEBUG < INFO < …...
Ubuntu下怎么配置vsftpd
2023年10月12日,周四中午 目录 首先要添加一个系统用户然后设置这个系统用户的密码给新创建的系统用户创建主目录启动vsftpd服务查看vsftpd服务的状态打开外界访问vsftpd服务所需的端口获取服务器的IP地址大功告成 首先要添加一个系统用户 useradd 用户名然后设置…...

链表(7.27)
3.3 链表的实现 3.3.1头插 原理图: newnode为新创建的节点 实现: //头插 //让新节点指向原来的头指针(节点),即新节点位于开头 newnode->next plist; //再让头指针(节点)指向新节点&#…...
在 Elasticsearch 中实现自动完成功能 1:Prefix queries
自动完成与搜索功能不同 - 我们应该在用户键入下一个字符后立即更新自动完成选项,每秒都会访问数据库,过滤数百万条记录,而不会导致任何性能下降! Elasticsearch 是一种可以轻松实现此类功能的技术,它是一种基于 Apac…...

『PyQt5-Qt Designer篇』| 13 Qt Designer中如何给工具添加菜单和工具栏?
13 Qt Designer中如何给工具添加菜单和工具栏? 1 创建默认窗口2 添加菜单栏3 查看和调用1 创建默认窗口 当新创建一个窗口的时候,默认会显示有:菜单栏和状态栏,如下: 可以在菜单栏上右键-移除菜单栏: 可以在菜单栏上右键-移除状态栏: 2 添加菜单栏 在窗口上,右键-创建…...
Android Studio新建项目教程
Android Studio新建项目教程 一、创建新项目 二、选择空白页项目类型 配置然后finish 等待项目完成初试化 等待初始化结束,创建完成...

前端页面布局之【响应式布局】
目录 🌟前言🌟优点🌟缺点🌟media兼容性🌟利用CSS3-Media Query实现响应式布局🌟常见的媒体类型🌟常见的操作符🌟属性值🌟设备检测🌟响应式阈值选取dz…...

定制排序小案例
案例:自定义 Book 类,里面包含 name 和 price,按 price 排序(从大到小)。 要求使用两种方式排序 , 有一个 Book[] books 4 本书对象. 使用前面学习过的传递 实现 Comparator 接口匿名内部类,也称为定制排序。 可以按照 price …...
如何设计一个ToC的弹窗
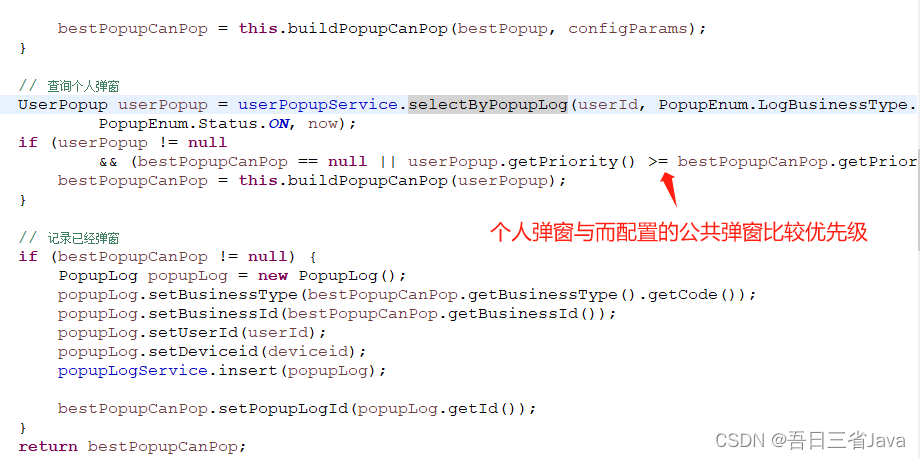
本文主要分享了如何设计一个具有高可扩展性的弹窗功能。 本设计参考了优惠券功能的设计思路,有兴趣的朋友可以看看优惠券的分享:如何设计一个可扩展的优惠券功能_java优惠券系统设计-CSDN博客 一、需求介绍 假如你的项目需要实现以下弹窗,…...
Idea执行Pom.xml导入jar包提示sun.misc.BASE64Encoder jar找不到---SpringCloud工作笔记197
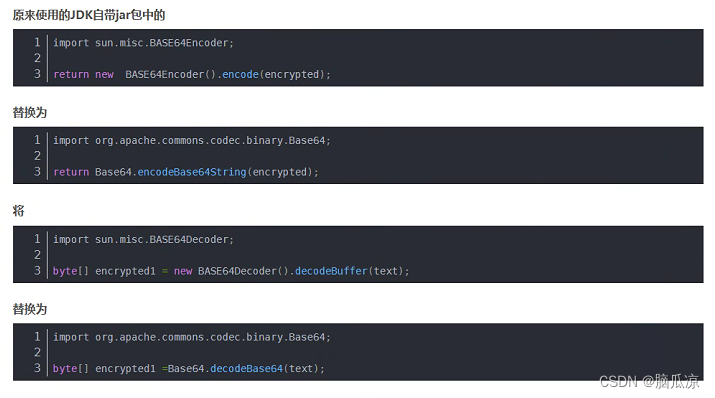
奇怪之前都是好好的,这个是因为,jdk的版本不对,重新打开以后自动被选择成jdk11了...记录一下 原因是从jdk9的时候,这个jar包已经被删除了,所以会报错,如果你用的是jdk自带的这个jar包就会报错,那么还可以,修改,不让他用jdk的,让他用 用org.apache.commons.codec.binary.Base64…...

大数据面试题:Spark和Flink的区别
面试题来源: 《大数据面试题 V4.0》 大数据面试题V3.0,523道题,679页,46w字 可回答:1)Spark Streaming和Flink的区别 问过的一些公司:杰创智能科技(2022.11),阿里蚂蚁(2022.11)&…...
 等级考试试卷(二级))
2023年9月青少年软件编程(C 语言) 等级考试试卷(二级)
2023年9月青少年软件编程(C 语言) 等级考试试卷(二级) 编程题 1.数组指定部分逆序重放 题目描述 将一个数组中的前k项按逆序重新存放。 例如,将数组8,6,5,4,1前3项逆序重放得到5,6,8,4,1。 输入 输入为两行ÿ…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
