【学习笔记】AGC055
A - ABC Identity
如果只有AAA,BBB两种字符的话,我们发现要寻找p∈[1,n]p\in [1,n]p∈[1,n],使得[1:p][1:p][1:p]中AAA的数目与[p+1:n][p+1:n][p+1:n]中BBB的数目相同。
如果有A,B,CA,B,CA,B,C三种字符,我们可以先将A,BA,BA,B分离出来,再将B,CB,CB,C分离出来,最后把A,CA,CA,C分离出来,这样最后会生成888个子序列 然后无法通过
神谕告诉我们,A,B,CA,B,CA,B,C三种字符一共只有666种本质不同的排列,因此我们可以考虑把原序列分成长度为nnn的333段,从每一段中分别选取一个字符构成A,B,CA,B,CA,B,C的排列,最后把相同的排列放在一起即可。猜一下结论,这显然是有解的。
这种题还是要多尝试
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
vector<int>v[3][3];
string s;
int n,res[600005];
int has(int x,int y,int z){return x*2+(y-(x<y))*1;
}
int main(){cin>>n>>s;for(int i=0;i<3*n;i++){v[i/n][s[i]-'A'].pb(i);}for(int i=1;i<=n;i++){for(int j=0;j<3;j++){for(int k=0;k<3;k++){for(int l=0;l<3;l++){if(v[0][j].size()&&v[1][k].size()&&v[2][l].size()&&j!=k&&k!=l&&j!=l){res[v[0][j].back()]=has(j,k,l);res[v[1][k].back()]=has(j,k,l);res[v[2][l].back()]=has(j,k,l);v[0][j].pop_back();v[1][k].pop_back();v[2][l].pop_back();}}}}}for(int i=0;i<3*n;i++)cout<<res[i]+1;
}
B - ABC Supremacy
如果只考虑SSS怎么生成TTT的话,怎么做都是O(n2)O(n^2)O(n2)的。数据删除
上面那种思路可能不太好处理 但是操作是可逆的,因此判断S,TS,TS,T同构的一个充分条件是它们都能到达一个相同的状态PPP。所以我们只要求出S,TS,TS,T的最小表示即可,这样一个字符串生成的表示是唯一的,就不用担心上述问题了。
剩下的就是怎么去寻找最小串。比较烦恼就先咕了
显然我们要凑出尽量多的ABCABCABC串(这里指轮换),并且每次操作相当于将ABCABCABC串这个整体挪到前面,然后把AAA放在最前面。那么BCBCBC是固定的吗?如果BCBCBC不是固定的,这个问题也比较烦恼,可以先咕着
开始慌张 不过幸运的是之前的结论还是正确的
我们可以把最小表示的定义换成 得到最多的ABCABCABC轮换组,那么BCBCBC就肯定是固定的了。
复杂度O(n)O(n)O(n)。
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
int n;
string s,t;
vector<char>solve(string s){vector<char>v;for(int i=0;i<s.size();i++){v.pb(s[i]);if(v.size()>=3&&(v[v.size()-3]=='A'&&v[v.size()-2]=='B'&&v[v.size()-1]=='C'||v[v.size()-3]=='B'&&v[v.size()-2]=='C'&&v[v.size()-1]=='A'||v[v.size()-3]=='C'&&v[v.size()-2]=='A'&&v[v.size()-1]=='B')){v.pop_back();v.pop_back();v.pop_back();}}return v;
}
int main(){cin>>n>>s>>t;cout<<(solve(s)==solve(t)?"YES":"NO");
}
C - Weird LIS
如果我们能思考清楚{Ai}\{A_i\}{Ai}合法的充要条件,那么这道题也就解决了。
或者说能建立双射然后计数也行
想不太清楚所以先咕了
思路其实并不困难,不过可能需要猜几个结论。
1.11.11.1 如果AiA_iAi全部等于KKK,猜测K≤⌊n2⌋K\le \lfloor\frac{n}{2}\rfloorK≤⌊2n⌋,这还是比较容易看出来。
1.21.21.2 如果KKK和K−1K-1K−1同时存在,那么Ai=K−1A_i=K-1Ai=K−1的那些点是固定的,我们要在所有Ai=KA_i=KAi=K的连续段中挑选一段接在固定的数之间,那么根据1.11.11.1的推论,这一段的长度不能超过⌊l2⌋\lfloor\frac{l}{2}\rfloor⌊2l⌋(lll表示连续段长度),我们猜测对于更小的情况也是取得到的,因此∑⌊li2⌋+cntK−1≥K\sum{\lfloor\frac{l_i}{2}\rfloor}+cnt_{K-1}\ge K∑⌊2li⌋+cntK−1≥K,并且cntK−1≤Kcnt_{K-1}\le KcntK−1≤K。
这个向下取整好像不太妙,先咕了
计数这个地方可能要多尝试
复杂度O(n2)O(n^2)O(n2)。不过要注意特判Ai=n−1A_i=n-1Ai=n−1的情况。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int N=5005;
int n,m,mod;
ll fac[N],inv[N],res;
ll pw(ll x,ll y=mod-2){ll z(1);for(;y;y>>=1){if(y&1)z=z*x%mod;x=x*x%mod;}return z;
}
void init(int n){fac[0]=1;for(int i=1;i<=n;i++)fac[i]=fac[i-1]*i%mod;inv[n]=pw(fac[n]);for(int i=n;i>=1;i--)inv[i-1]=inv[i]*i%mod;
}
ll binom(int x,int y){if(x<0||y<0||x<y)return 0;return fac[x]*inv[y]%mod*inv[x-y]%mod;
}
int main(){cin>>n>>m>>mod,init(n+1);for(int x=1;x<n;x++){for(int y=0;y<=(n-x)/2;y++){int L=max(3,x),R=min(m,x+y);if(L<=R)res=(res+binom(x+y,x)*binom(x+1,n-x-2*y)%mod*(R-L+1))%mod;}}for(int i=2;i<=min(m,n/2);i++)res++;if(m==n-1)res++;cout<<res%mod;
}
D - ABC Ultimatum
先考虑怎么判断给定串合法。
好像没什么思路先咕了
不过这题还是有学习的价值的,我们可以照着结论来翻译一下
设Sa(i),Sb(i),Sc(i)S_a(i),S_b(i),S_c(i)Sa(i),Sb(i),Sc(i)表示1∼i1\sim i1∼i中a,b,ca,b,ca,b,c的个数,Ma=max(Sb(i)−Sa(i)),Mb=max(Sc(i)−Sb(i)),Mc=max(Sa(i)−Sc(i))M_a=\max (S_b(i)-S_a(i)),M_b=\max(S_c(i)-S_b(i)),M_c=\max(S_a(i)-S_c(i))Ma=max(Sb(i)−Sa(i)),Mb=max(Sc(i)−Sb(i)),Mc=max(Sa(i)−Sc(i)),则SSS是好的当且仅当Ma+Mb+Mc≤nM_a+M_b+M_c\le nMa+Mb+Mc≤n
必要性应该很显然,可以猜一个结论,或者打表证明这是充要的。
可能有时间会补一下证明
然后暴力复杂度O(n7)O(n^7)O(n7)。但是很显然可以省去一维状态,因此就可以在O(n6)O(n^6)O(n6)时间内通过了。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int mod=998244353;
int n,dp[17][17][17][17][17][17],res;
string s;
void add(int &x,int y){if((x+=y)>=mod)x-=mod;
}
int main(){cin>>n>>s;dp[0][0][0][0][0][0]=1;for(int i=0;i<3*n;i++){for(int a=0;a<=n;a++){for(int b=0;b<=n;b++){int c=i-a-b;if(c>n||c<0)continue;for(int j=0;j<=n;j++){for(int k=0;k<=n;k++){for(int l=0;l<=n;l++){int tmp=dp[a][b][c][j][k][l];if(s[i]=='A'||s[i]=='?'){add(dp[a+1][b][c][j][k][max(l,a+1-c)],tmp);}if(s[i]=='B'||s[i]=='?'){add(dp[a][b+1][c][max(b+1-a,j)][k][l],tmp);}if(s[i]=='C'||s[i]=='?'){add(dp[a][b][c+1][j][max(c+1-b,k)][l],tmp);}}}}}}}for(int i=0;i<=n;i++){for(int j=0;j<=n;j++){for(int k=0;k<=n;k++){if(i+j+k<=n)add(res,dp[n][n][n][i][j][k]);}}}cout<<res;
}
E - Set Merging
场上无一人AC
这种给你规定输入的构造题就很烦,那么我们就要去分析一些性质,看它在不同情况下是否成立。
某个人曾经说过,第一个做出这种题的人一定是具有非凡的人类智慧的
相关文章:

【学习笔记】AGC055
A - ABC Identity 如果只有AAA,BBB两种字符的话,我们发现要寻找p∈[1,n]p\in [1,n]p∈[1,n],使得[1:p][1:p][1:p]中AAA的数目与[p1:n][p1:n][p1:n]中BBB的数目相同。 如果有A,B,CA,B,CA,B,C三种字符,我们可以先将A,BA,BA,B分离出来…...
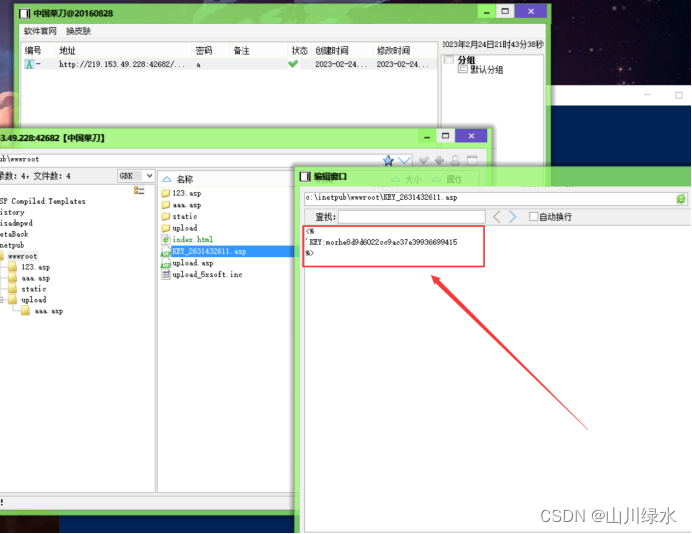
墨者——内部文件上传系统漏洞分析溯源 内部文件上传系统漏洞分析溯源
墨者——内部文件上传系统漏洞分析溯源 内部文件上传系统漏洞分析溯源 1.选择合适的文件上传 2.可以看到为*.asp文件 3.可以推测出此站点为IIS 4.上传shell.asp试试 5.上传报错,将其改名为shell.asp.txt上传,发现上传成功 6.有个问题就是服务器将我们所…...

5.2 Python if语句
5.2.3 检查是否不相等要判断两个值是否不等,可结合使用惊叹号和等号(!),其中的惊叹号表示不,在很多编程语言中都如此。下面再使用一条if语句来演示如何使用不等运算符。我们将把要求的比萨配料存储在一个变量中,再打印一条消息&am…...

ubuntu gerrit 配置
1 - 简介 参考地址: https://www.cnblogs.com/anliven/p/12019974.html https://www.cnblogs.com/anliven/p/11980432.html 虽然Gerrit 本身提供 Code Review和 Git 仓库的两大功能,但实际上很多项目用的是其他的Git仓库,例如GitLab和GitHub。 一般情况下,Gerrit位于最终…...

运动蓝牙耳机什么牌子好,运动蓝牙耳机品牌推荐
现在市面上运动耳机的品牌越来越多,还不知道选择哪一些运动耳机品牌,可以看看下面的一些耳机分享,运动耳机需要注意耳机的参数配置以及佩戴舒适度,根据自己最根本的使用需求来选择运动耳机。 1、南卡Runner Pro4骨传导蓝牙运动耳…...
C#传智:方法及参数、重载(第7天))
(7)C#传智:方法及参数、重载(第7天)
一、方法作用域 被调用者需要调用者的值,方法有二: 1.传参数. private static void Main(string[] args){int m 3;Console.WriteLine(m);Console.ReadKey();}public static int GetMax(int m){return m 3;} 2.使用静态字段模拟全局. 多个方法都需要时&#x…...

Python 函数式编程
函数式编程:允许把函数本身作为参数传入另一个函数,还允许返回一个函数! 1.高阶函数 一个函数可以接收另一个函数作为参数,这种函数称之为高阶函数 abs(-10) 是函数调用 abs是函数本身 abs函数名其实是一个变量名 变量可以…...
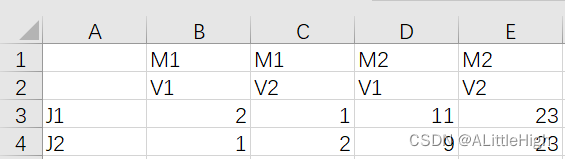
pandas读取EXCEL列名重复问题解决——pandas设置多行为列名(多层列名)
问题呈现 这是我在问答区看到的一个问题。 问:在python中使用pandas读取Excel数据,重复数据被区分了,如何做到重复数据不被区分? 解决思路 很明显,这是pandas读取excel文件时列名设置问题,我第一时间想…...

CMake常用语法
1. cmake_minimum_required(VERSION 3.4.1) 指定需要的最小的cmake版本 2. aux_source_directory 查找源文件并保存到相应的变量中: #查找当前目录下所有源文件并保存至SRC_LIST变量中 aux_source_directory(. SRC_LIST)3. add_library 3.1 添加一个库 add_library(<n…...
基础知识)
Java知识复习(一)基础知识
1、什么是JVM、JDK和JRE? JVM是指运行Java字节码的虚拟机。而字节码文件指的就是扩展名为.class的文件,JDK指功能齐全的Java SDK,能够创建和编译程序JRE指Java运行的环境,包括JVM、类库和命令等 2、重载和重写的主要区别 重载&…...
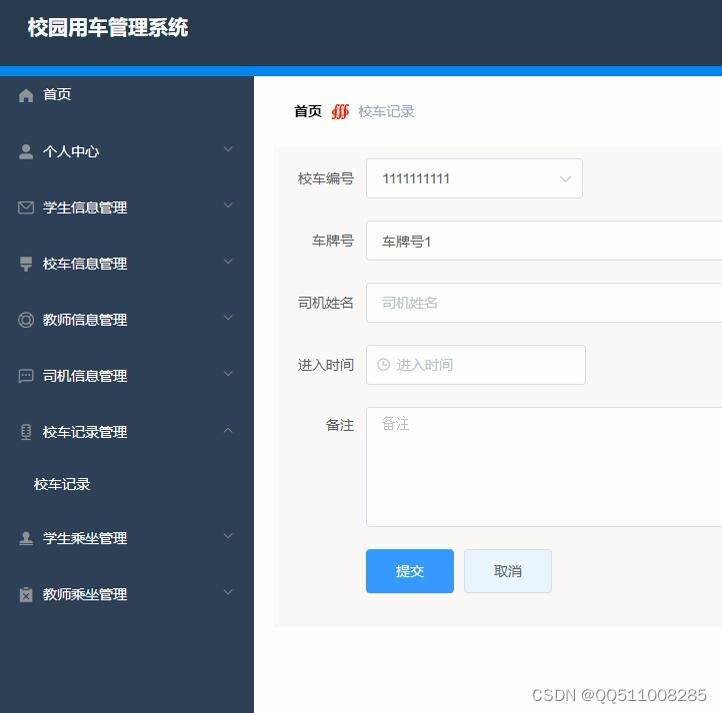
springboot+vue.js校园车辆用车预约管理系统
springboot是基于spring的快速开发框架, 相比于原生的spring而言, 它通过大量的java config来避免了大量的xml文件, 只需要简单的生成器便能生成一个可以运行的javaweb项目, 是目前最火热的java开发框架 前端技术:nodejsvueelementui本项目的应用场景描述如下&…...

【 K8s 源码之调度学习】Pod 间亲和性和反亲和性的源码分析
查看案例 字段含义podAffinityPod 间的亲和性定义podAntiAffinityPod 间的反亲和性定义requiredDuringSchedulingIgnoredDuringExecution硬性要求,必须满足条件,保证分散部署的效果最好使用用此方式preferredDuringSchedulingIgnoredDuringExecution软性…...

计及绿证交易及碳排放的含智能楼宇微网优化调度(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
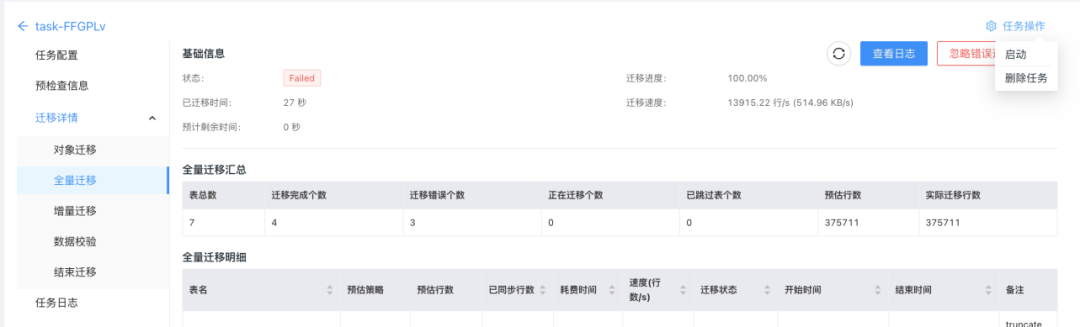
场景扩展,体验升级 | DBMotion新增无公网数据库迁移、支持监控报警等多项功能
丝滑的零停机数据库在线迁移工具——DBMotion,又双叒叕发新版:新增的网关、数据源功能,让你无公网IP的数据库也可以迁移;新增的监控功能,让你对迁移性能一目了然;新增的报警功能,让你及时获得同…...
【正点原子FPGA连载】第十五章eMMC读写测试实验 摘自【正点原子】DFZU2EG_4EV MPSoC之嵌入式Vitis开发指南
1)实验平台:正点原子MPSoC开发板 2)平台购买地址:https://detail.tmall.com/item.htm?id692450874670 3)全套实验源码手册视频下载地址: http://www.openedv.com/thread-340252-1-1.html 第十五章eMMC读写…...
i2c子系统
i2c 硬件协议 Linux 应用层读写i2c 数据 在Linux系统上,不仅可以在内核中使用 i2c 总线发送、接收数据,同时也支持应用层使用i2c 总线发送、接收。 如果在内核中使能了drivers/i2c/i2c-dev.c 配置,内核就会为每一个i2c 控制器生成一个/dev/…...

【K3s】第17篇 Helm版本和支持的Kubernetes版本对照表
目录 Helm版本和支持的Kubernetes版本对照表 Helm版本和支持的Kubernetes版本对照表 描述了在Helm和Kubernetes之间支持的最大版本偏差。 Helm的版本用 x.y.z 描述,x是主版本,y是次版本,z是补丁版本。 当一个Helm的新版本发布时࿰…...
如何自己搭建一个ai画图系统? 从0开始云服务器部署novelai
如何自己搭建一个ai画图系统? 从0开始云服务器部署novelai 上面两张图都是通过ai生成的,是不是有以假乱真的感觉。 本教程提供的是自己搭建一个可以外网访问的ai系统的方法,需要采购gpu服务器(后续会出白嫖的方式)&…...

SpringSecurity过滤请求导致的系统bug
背景 今天开发一个新的会员管理系统,继承了SpringSecurity的,用以控制权限。结果无论怎么配置,都会报错:An Authentication object was not found in the SecurityContext 这句话的意思很明确:指的就是在SecurityCon…...

css\js\vue知识点
1.css3新特性 css3新特性 1)选择器 2)阴影 3)形状转换(2D <-> 3D) 4)变形 5)动画(过渡动画、帧动画) 6)边框 7)多重背景 8)反…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...

VSCode 使用CMake 构建 Qt 5 窗口程序
首先,目录结构如下图: 运行效果: cmake -B build cmake --build build 运行: windeployqt.exe F:\testQt5\build\Debug\app.exe main.cpp #include "mainwindow.h"#include <QAppli...
