图论-最短路径算法-弗洛伊德算法与迪杰斯特拉算法
弗洛伊德算法:
弗洛伊德算法本质是动态规划,通过添加点进如可选择的点组成的集合的同时更新所有点之间的距离,从而得到每两个点之间的最短距离。
-
初始化: 创建一个二维数组
dist,其中dist[i][j]表示从节点i到节点j的最短路径的权重。将对角线上的元素初始化为0,表示节点到自身的距离。如果存在直接相连的边,则将dist[i][j]初始化为这些边的权重;否则,初始化为一个大数表示无穷大。 -
三重循环: 对于每一对节点
(i, j),以及所有可能的中间节点k,进行三重循环:plaintextCopy code
for k from 1 to n: for i from 1 to n: for j from 1 to n: dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])在每一次迭代中,检查是否通过中间节点
k能够获得更短的路径。如果dist[i][k] + dist[k][j]小于当前已知的dist[i][j],则更新dist[i][j]。 -
输出结果: 算法结束后,矩阵
dist中的元素即为图中所有节点对之间的最短路径。
迪杰斯特拉算法:
迪杰斯特拉算法是广度优先遍历算法的一种,遍历当前节点的所有邻接点,更新原点到邻接点的距离。最终得到原点到每个点的最小距离。
-
初始化: 创建两个数组,
distance和visited。distance数组用于存储从起始节点到各个节点的当前最短路径长度,初始时将起始节点到自身的距离设置为0,其他节点的距离设置为无穷大。visited数组用于标记节点是否已经被访问,初始时所有节点都未被访问。 -
选择起始节点: 将起始节点标记为当前的工作节点。
-
更新邻接节点的距离: 遍历当前工作节点的所有邻接节点,计算从起始节点经过当前工作节点到邻接节点的路径长度。如果这个路径长度小于
distance数组中记录的邻接节点的当前最短路径长度,则更新distance数组。 -
选择下一个工作节点: 从未访问的节点中选择一个具有最小最短路径长度的节点,将其标记为当前的工作节点。如果所有未访问的节点都具有无穷大的最短路径长度,说明剩下的节点不可达,算法结束。
-
重复步骤3和4: 重复执行步骤3和步骤4,直到所有节点都被访问过。
案例题目
现在小丽在城镇A,小明在城镇B。小丽要出发找小明。
城镇之间有双向通行的道路,通过道路要消耗一定的时间。
其中已知城镇C和城镇D之间有双向的传送门,可以不消耗时间瞬间传送过去
现在请你求出小丽从城镇A抵达城镇B的最短时间。保证从起点到终点有路径可达。
输入描述
第一行两个正整数n,m,以空格分开,表示总共有n个城镇,有m条道路相连
第二行两个正整数A,B,以空格分开,分别表示小丽所在城镇A,小明所在城镇B。
第三行两个正整数C,D,以空格分开,表示城镇C和城镇D之间有瞬间的双向传送门。
接下来m行,每行三个正整数u,v, c,以空格分开,表示城镇u和城镇v之间有道路,通过道路消耗时间c。
对于100%的数据保证 1<=n <=100,1<=m<=2*n,每条道路的时间花费在[1,10]之间
输出描述
一行,一个整教表示最短到达时间。
样例输入
4 3
1 4
1 3
1 2 1
2 3 1
2 4 1
样例输出
2代码
弗洛伊德算法
n,m = map(int,input().split(" "))
A,B = map(int,input().split(" "))
print(A,B)
C,D = map(int,input().split(" "))
dis = [[float('inf') for i in range(n+1)] for j in range(n+1)]
for i in range(m):u,v,c = map(int,input().split(" "))dis[u][v] = cdis[v][u] = cdis[C][D] = dis[D][C] = 0for k in range(1,n+1):for i in range(1,n+1):for j in range(1,n+1):dis[i][j] = min(dis[i][j],dis[i][k]+dis[k][j])print(dis[A][B])迪杰斯特拉算法
import collectionsn,m = map(int,input().split(" "))
A,B = map(int,input().split(" "))
C,D = map(int,input().split(" "))graph = [[] for _ in range(n)]
for i in range(m):u,v,c = map(int,input().split(" "))graph[u-1].append((v-1,c))graph[v- 1].append((u-1,c))graph[C-1].append((D-1,0))
graph[D-1].append((C-1,0))def dijkstra(graph,start,end):n = len(graph)distances = [float('inf') for i in range(n)]distances[start] = 0queue = collections.deque( [(0,start)])vis = [False] * nwhile queue:current_distance,current_node = queue.popleft();if vis[current_node]:continuevis[current_node] = Truefor neighbor,weight in graph[current_node]:new_distance = current_distance + weightif new_distance < distances[neighbor]:distances[neighbor] = new_distancequeue.append((new_distance,neighbor))return distances[end]print(dijkstra(graph,A-1,B-1))相关文章:

图论-最短路径算法-弗洛伊德算法与迪杰斯特拉算法
弗洛伊德算法: 弗洛伊德算法本质是动态规划,通过添加点进如可选择的点组成的集合的同时更新所有点之间的距离,从而得到每两个点之间的最短距离。 初始化: 创建一个二维数组 dist,其中 dist[i][j] 表示从节点 i 到节点…...

[23] IPDreamer: Appearance-Controllable 3D Object Generation with Image Prompts
pdf Text-to-3D任务中,对3D模型外观的控制不强,本文提出IPDreamer来解决该问题。在NeRF Training阶段,IPDreamer根据文本用ControlNet生成参考图,并将参考图作为Zero 1-to-3的控制条件,用基于Zero 1-to-3的SDS损失生成…...

深入理解React中的useEffect钩子函数
引言: React是一种流行的JavaScript库,它通过组件化和声明式编程的方式简化了前端开发。在React中,一个核心概念是组件的生命周期,其中包含了许多钩子函数,用于管理组件的不同阶段。其中之一就是useEffect钩子函数&…...

数字化时代的财务管理:挑战与机遇
导语:随着数字化技术的不断发展,财务管理正面临着前所未有的挑战和机遇。数字化不仅改变了财务数据的收集、处理和分析方式,还为财务决策提供了更多的依据和方向。本文将探讨数字化时代财务管理的新特点,以及如何利用数字化技术提…...
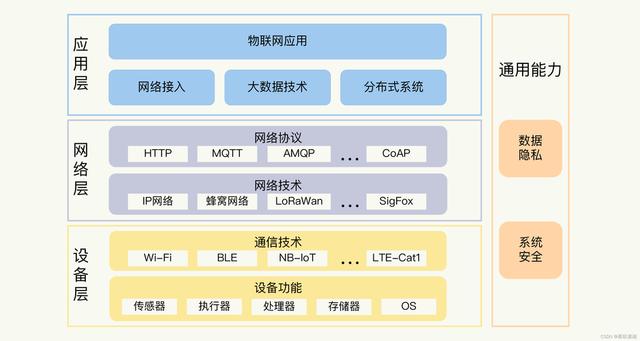
网络通信协议-HTTP、WebSocket、MQTT的比较与应用
在今天的数字化世界中,各种通信协议起着关键的作用,以确保信息的传递和交换。HTTP、WebSocket 和 MQTT 是三种常用的网络通信协议,它们各自适用于不同的应用场景。本文将比较这三种协议,并探讨它们的主要应用领域。 HTTPÿ…...
、dataloader、长短期记忆网络(LSTM)、门控循环单元(GRU)、超参数对比)
【深度学习】深度学习实验四——循环神经网络(RNN)、dataloader、长短期记忆网络(LSTM)、门控循环单元(GRU)、超参数对比
一、实验内容 实验内容包含要进行什么实验,实验的目的是什么,实验用到的算法及其原理的简单介绍。 1.1 循环神经网络 (1)理解序列数据处理方法,补全面向对象编程中的缺失代码,并使用torch自带数据工具将数据封装为dataloader。 (2)分别采用手动方式以及调用接口方式…...

DB2分区表详解
一、分区表基本概念 当表中的数据量不断增大,查询数据的速度就会变慢,应用程序的性能就会下降,这时就应该考虑对表进行分区。分区后的表称为分区表。 表进行分区后,逻辑上表仍然是一张完整的表,只是将表中的数据在物理上存放到多个“表空间”(物理文件上),这样查询数据时…...

基本地址变换机构
基本地址变换机构:用于实现逻辑地址到物理地址转换的一组硬件机构。 关于页号页表的定义,放个本人的传送门 1.页表寄存器 基本地址变换机构可以借助进程的页表将逻辑地址转换为物理地址。 1.作用 通常会在系统中设置一个页表寄存器(PTR&…...
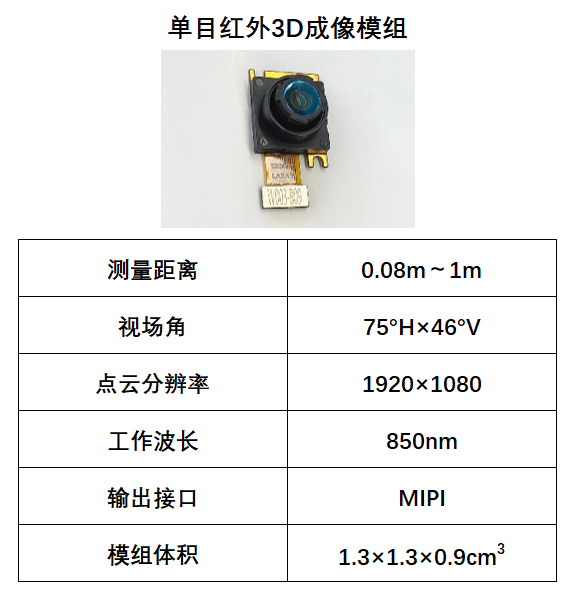
以单颗CMOS摄像头重构三维场景,维悟光子发布单目红外3D成像模组
维悟光子近期发布全新单目红外3D成像模组,现可提供下游用户进行测试导入。通过结合微纳光学元件编码和人工智能算法解码,维悟光子单目红外3D成像模组采用单颗摄像头,通过单帧拍摄,可同时获取像素级配准的3D点云和红外图像信息,可被应用于机器人、生物识别等广阔领域。 市场…...
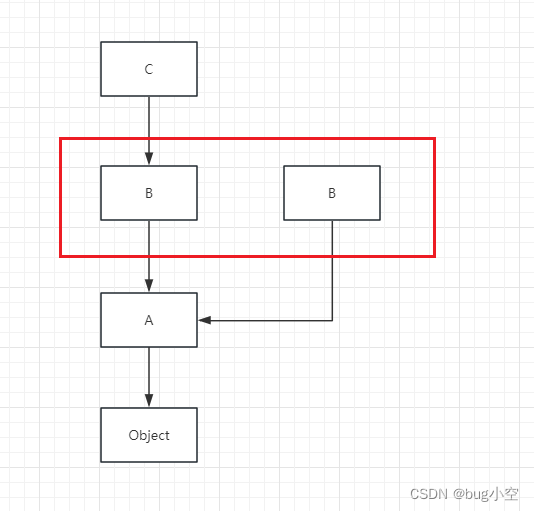
Jinja2模板注入 | python模板注入特殊属性 / 对象讲解
在进行模板利用的时候需要使用特殊的属性和对象进行利用,这里对这些特殊属性及方法进行讲解 以下实验输出python3版本为 3.10.4, python2版本为 2.7.13 特殊属性 __class__ 类实例上使用,它用于获取该实例对应的类__base__ 用于获取父类__mr…...

一致性公式证明
首先,假设存在两个不同的聚类假设 f 1 f^1 f1和 f 2 f^2 f2,它们在两个视角上的聚类结果分别为 y 1 ∈ { − 1 , 1 } n y^1\in\{-1,1\}^n y1∈{−1,1}n和 y 2 ∈ { − 1 , 1 } n y^2\in\{-1,1\}^n y2∈{−1,1}n。 证明一致性不等式: …...
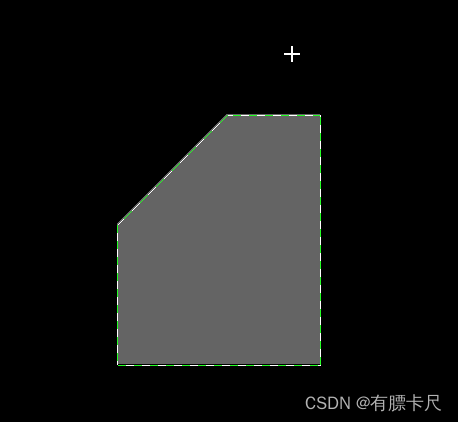
allegro中shape的一些基本操作(一)——添加和修改shape
添加shape 简单添加shape的方式有3种,如下图所示 点击选择相应的shape模式后可以在option面板中设置相应的shape参数(这里不做过多介绍,里面可以设置shape的大小、静态或动态shape等参数),然后再用鼠标在相应的层上添…...
HBuilder创建uniapp默认项目导入uview(胎教)
1:更新HBuilder 建议更新 2:更新插件 我本人在没有更新插件的情况下报错了,找到了**这个大佬**解决问题,所以建议更新插件 先卸载uni-app(Vue2)编译 再重新安装 uni-app(Vue2)…...

C语言基础算法复习
003 斐波那契数列问题 #include<stdio.h> int main() {int i,f11,f21,f3,num;printf("%5d %5d",f1,f2);num2;for(i1; i<18; i){f3f1f2;f1f2;f2f3;num;printf("%5d",f3);if(num%40) printf("\n");}return 0; }//#输数斐波那契数列的前20…...
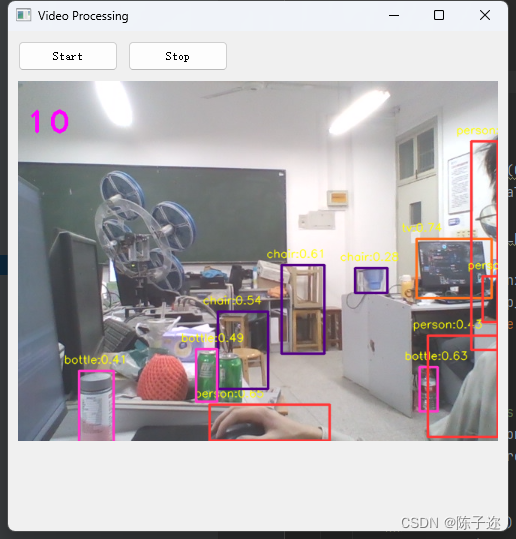
PyQt界面里如何加载本地视频以及调用摄像头实时检测(小白入门必看)
目录 1.PyQt介绍 2.代码实现 2.1实时调用摄像头 2.2 使用YOLOv5推理 2.3 代码中用到的主要函数 1.PyQt介绍 PyQt是一个用于创建桌面应用程序的Python绑定库,它基于Qt框架。Qt是一个跨平台的C应用程序开发框架,提供了丰富的图形界面、网络通信、数据…...
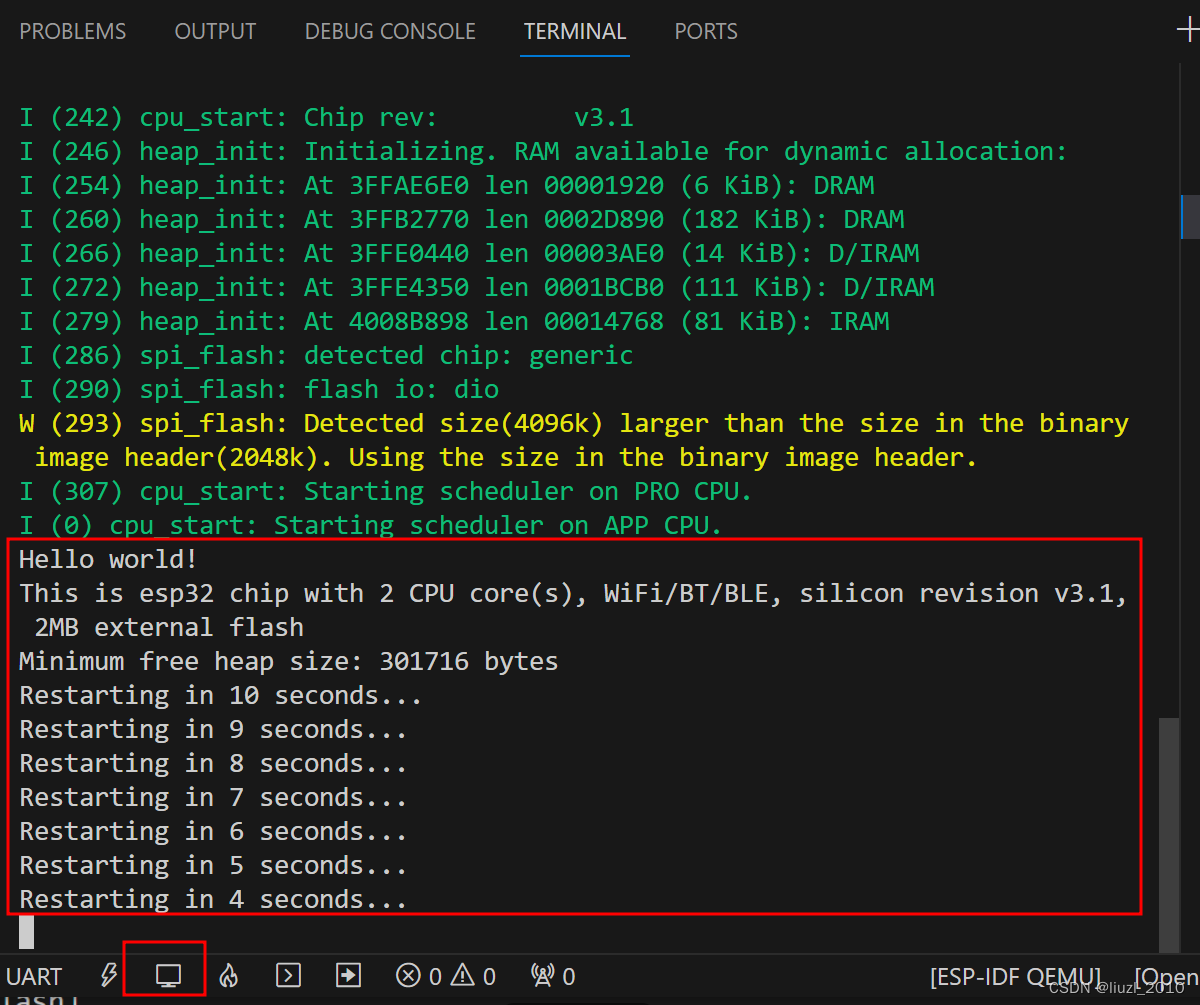
Ubuntu:VS Code IDE安装ESP-IDF【保姆级】
物联网开发学习笔记——目录索引 参考: VS Code官网:Visual Studio Code - Code Editing. Redefined 乐鑫官网:ESP-IDF 编程指南 - ESP32 VSCode ESP-ID Extension Install 一、前提条件 Visual Studio Code IDE安装ESP-IDF扩展&…...

软考高级系统架构设计师系列之:快速掌握软件工程核心知识点
软考高级系统架构设计师系列之:快速掌握软件工程核心知识点 一、软件开发方法二、软件开发模型三、软件开发模型-瀑布模型四、软件开发模型-经典模型汇总五、软件开发模型-增量模型与螺旋模型六、软件开发模型-V模型七、软件开发模型-构件组装模型八、软件开发模型-统一过程九…...

Java基础面试-ArrayList和LinkedList的区别
ArrayList: 基于动态数组,连续内存存储,适合下标访问(随机访问),扩容机制: 因为数组长度固定,超出长度存数据时需要新建数组,然后将老数组的数据拷贝到新数组,如果不是尾部插入数据还会涉及到元素的移动(往…...

如何从 Pod 内访问 Kubernetes 集群的 API
Kubernetes API 是您检查和管理集群操作的途径。您可以使用Kubectl CLI、工具(例如curl)或流行编程语言的官方集成库来使用 API 。 该 API 也可供集群内的应用程序使用。Kubernetes Pod 会自动获得对 API 的访问权限,并且可以使用提供的服务帐户进行身份验证。您可以通过使…...

计网面试复习自用
五层: 应用层:应用层是最高层,负责为用户提供网络服务和应用程序。在应用层,用户应用程序与网络进行交互,发送和接收数据。典型的应用层协议包括HTTP(用于网页浏览)、SMTP(用于电子邮…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
