当前位置： 首页 > news >正文

近万字概述L3及以上自动驾驶故障运行和故障安全机制

news 文章来源：https://blog.csdn.net/xiaoming0907/article/details/128027550 2025/4/28 16:11:15

本文描述了对ADS的FO和FS机制的评估方法。当系统不能按预期运行时，ADS将使用FO和FS机制。这些机制使ADS能够在最大程度上达到使车辆及其乘员脱离危险的MRC。定义、测试和验证实现MRC的FO和FS策略是确保ADS安全运行和部署的重要步骤。

MRC在SAE J3016中被定义为：

用户或ADS在执行DDT接管后可使车辆达到的状态，以减少在特定行程不能或不应该完成时发生碰撞的风险。

SAE J3016进一步指出：

在L3级，考虑到ADS或车辆的DDT性能相关的系统故障，DDT准备接管的用户在确定有必要时，应达到最小风险的状态。

在L4级和L5级，ADS能够在必要时（即，由于ODD退出，如果适用，或ADS与DDT性能相关的系统故障）自动实现最小风险条件。在L4级和L5级自动实现最小风险条件的特点将根据系统故障的类型和程度、有关ADS功能的ODD（如果有）以及系统故障或ODD退出发生时的特定操作条件而变化。它可能需要自动将车辆停在其当前的行驶路线上，也可能需要一个更广泛的操作，旨在将车辆从一个有效的车道上移开和/或将车辆自动返回到调度设施。

如《万字概述L3级及以上自动驾驶测试和评估方法》所述，样本测试框架包括

相关文章：

近万字概述L3及以上自动驾驶故障运行和故障安全机制

本文描述了对ADS的FO和FS机制的评估方法。当系统不能按预期运行时，ADS将使用FO和FS机制。这些机制使ADS能够在最大程度上达到使车辆及其乘员脱离危险的MRC。定义、测试和验证实现MRC的FO和FS策略是确保ADS安全运行和部署的重要步骤。 MRC在SAE J3016中被定义为： 用户或ADS在…...

编程日记 2023/3/17 3:28:54

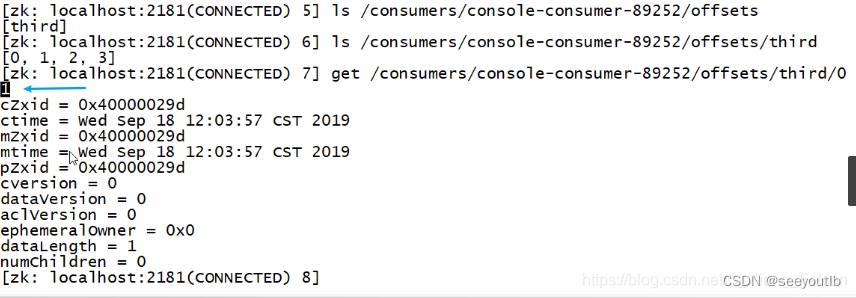
kafka入门到精通

文章目录一、kafka概述？1.定义1.2消息队列1.2.1 传统消息队列的使用场景1.2.2 消息队列好处1.2.3 消息队列两种模式1.3 kafka基础架构二、kafka快速入门1.1使用docker-compose安装kafka1.2测试访问kafka-manager1.3 查看kafka版本号1.4 查看zookeeper版本号1.5 扩展…...

编程日记 2023/3/15 12:33:08

es-09模糊查询

模糊查询 前缀搜索&#xff1a;prefix 概念&#xff1a;以xx开头的搜索&#xff0c;不计算相关度评分。 注意&#xff1a; 前缀搜索匹配的是term&#xff0c;而不是field。前缀搜索的性能很差前缀搜索没有缓存前缀搜索尽可能把前缀长度设置的更长 语法&#xff1a; GET <ind…...

编程日记 2023/2/25 11:03:33

57 - 深入解析任务调度

---- 整理自狄泰软件唐佐林老师课程 文章目录1. 问题1.1 思考1.2 实例分析&#xff1a;问题分析及解决2. 深入讨论2.1 任务调度的定义2.2 关于调度算法的分类2.3 什么时候进行任务调度2.4 任务的分类2.5 关于优先级调度2.6 问题2.7 调度算法的终极目标2.8 课后扩展1. 问题 系统…...

编程日记 2023/4/2 2:50:46

CAN总线开发一本全（3） - 微控制器集成的FlexCAN外设

CAN总线开发一本全&#xff08;3&#xff09; - 微控制器集成的FlexCAN外设 苏勇&#xff0c;2023年2月 文章目录CAN总线开发一本全&#xff08;3&#xff09; - 微控制器集成的FlexCAN外设引言硬件外设模块系统概要总线接口单元 - 寄存器清单数据结构 - 消息缓冲区MB初始化过…...

编程日记 2023/3/15 12:34:17

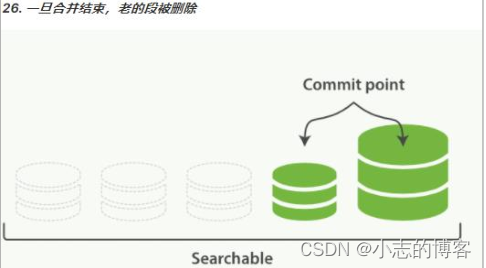
Elasticsearch7.8.0版本进阶——段合并

目录一、段的概述1.1、段的概念1.2、段的缺点1.3、如何解决段数量暴增问题二、段合并的流程三、段合并的注意事项一、段的概述 1.1、段的概念 每一 段 本身都是一个倒排索引。 1.2、段的缺点 由于自动刷新流程每秒会创建一个新的段 &#xff0c;这样会导致短时间内的段数量…...

编程日记 2023/4/2 15:10:13

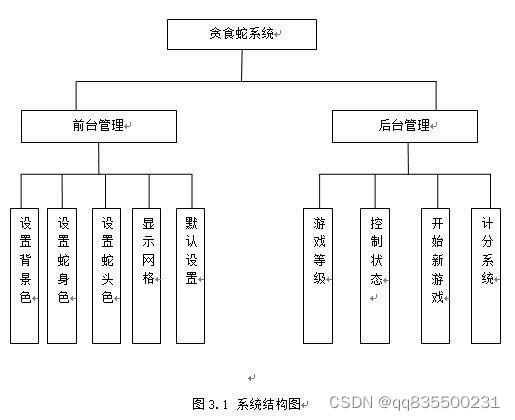
Java版贪食蛇游戏

技术&#xff1a;Java等摘要&#xff1a;近年来Java作为一种新的编程语言&#xff0c;以其简单性、可移植性和平台无关性等优点&#xff0c;得到了广泛地应用&#xff0c;特别是Java与万维网的完美结合&#xff0c;使其成为网络编程和嵌入式编程领域的首选编程语言。MyEclipse是…...

编程日记 2023/4/2 15:11:38

2023年度数学建模竞赛汇总

本人7年数学建模竞赛经验&#xff0c;历史获奖率百分之百。团队成员都是拿过全国一等奖的硕博&#xff0c;有需要数模竞赛帮助的可以私信我。 下面主要列几年一些比较有含金量的数学建模竞赛&#xff08;按比赛时间顺序&#xff09; 1. 美国大学生数学建模竞赛 报名时间&…...

编程日记 2023/3/16 21:19:10

了解Python语言和版本

1.1 任务1了解Python语言和版本 Python 语言的名字来自于一个著名的电视剧"Monty Pythons Flying Cireus",Python之父 Guido van Rossum是这部电视剧的狂热爱好者&#xff0c;所以把他设计的语言命名为Python。 Python 是一门跨平台、开源、免费的解释型高级动态编…...

编程日记 2023/3/22 15:20:16

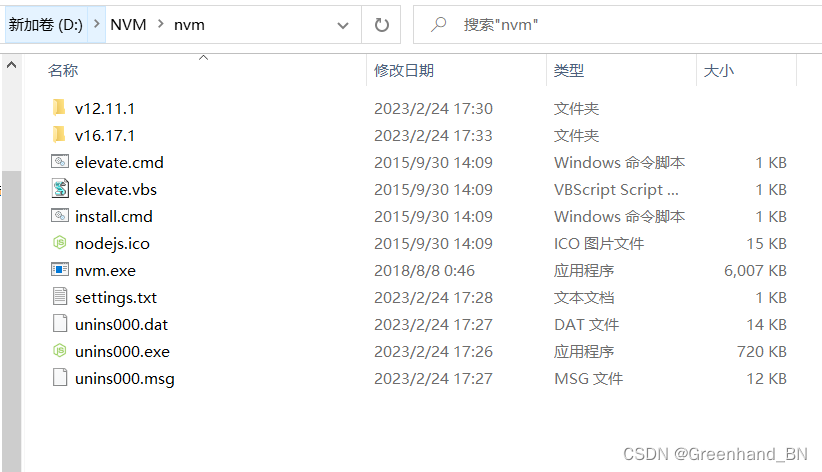
nvm （node版本管理工具）安装的详细步骤，并解决安装过程中遇到的问题

1、下载NVM&#xff0c;跳转下载链接后&#xff0c;如下图&#xff0c;下载红框后解压文件 2、安装 注意&#xff1a;双击安装之后&#xff0c;会有两个地址选择&#xff0c; 1、地址中不能存在空格 2、不要放在C盘中&#xff0c;后面需要改个设置文件&#xff0c;安装到C盘的…...

编程日记 2023/4/1 3:02:17

朴素贝叶斯笔记

贝叶斯公式在A 条件成立下&#xff0c;B的概率等于B的概率*在B条件成立下&#xff0c;A的概率/A的概率&#xff0c;推导假设一个学校中男生占总数的60%&#xff0c;女生占总数的40%。并且男生总是穿长裤&#xff0c;女生则一半穿长裤、一半穿裙子。1.正向概率。随机选取一个学生…...

编程日记 2023/3/15 12:38:59

【GUI】用于电动助力车性能分析的GUI(Matlab代码实现）

&#x1f468;‍&#x1f393;个人主页&#xff1a;研学社的博客&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5;&#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密…...

编程日记 2023/3/18 8:11:02

Android：反编译apk踩坑/apktool/dex2jar/JDGUI

需求描述 想要反编译apk文件&#xff0c;搜到了这篇博客&#xff1a;Android APK反编译就这么简单 详解&#xff08;附图&#xff09;&#xff0c;非常有参考价值~但其中的工具下载链接都已404&#xff0c;而本杂鱼实际操作的过程中也出现了亿点点点点点点的问题&#xff0c;于…...

编程日记 2023/3/15 12:40:28

React 跨域的配置

1、为什么会出现跨域&#xff1f; 浏览器遵循同源政策&#xff08;同源策略三要素&#xff1a;协议相同、域名相同、端口相同&#xff09; 2、配置跨域代理 使用中间件 http-proxy-middleware&#xff08;安装依赖&#xff09; npm install http-proxy-middleware 创建setupP…...

编程日记 2023/3/21 11:32:49

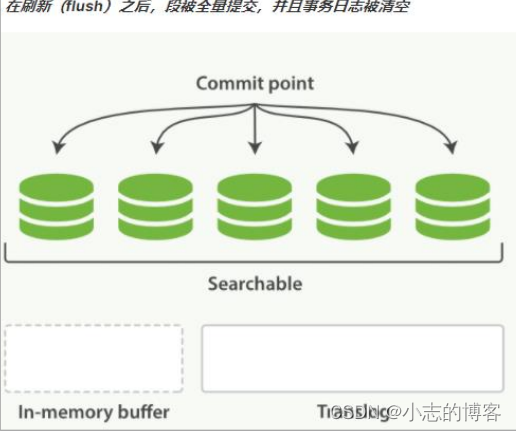
Elasticsearch7.8.0版本进阶——持久化变更

目录一、持久化变更的概述二、事务日志&#xff08;translog&#xff09;三、持久化变更完整流程四、事务日志&#xff08;translog&#xff09;的作用五、事务日志&#xff08;translog&#xff09;的目的一、持久化变更的概述 没有用 fsync 把数据从文件系统缓存刷&#xff…...

编程日记 2023/3/15 23:56:30

CF Edu 127 A-E vp补题

CF Edu 127 A-D vp补题 继续每日一vp&#xff0c;今天晚上有课&#xff0c;时间不太多&#xff0c;回去就直接vp。前三题比较简单&#xff0c;过了之后排名rk2000&#xff0c;然后就去洗澡了。d题没怎么认真思考&#xff0c;其实也可做。最后rk4000。发挥还行&#xff0c;b题罚…...

编程日记 2023/4/1 12:37:55

剑指 Offer 05. 替换空格

摘要 剑指 Offer 05. 替换空格 一、字符替换 由于每次替换从1个字符变成3个字符&#xff0c;使用字符数组可方便地进行替换。建立字符数组地长度为 s 的长度的3倍&#xff0c;这样可保证字符数组可以容纳所有替换后的字符。 获得 s 的长度 length创建字符数组 array&#x…...

编程日记 2023/2/25 10:45:27

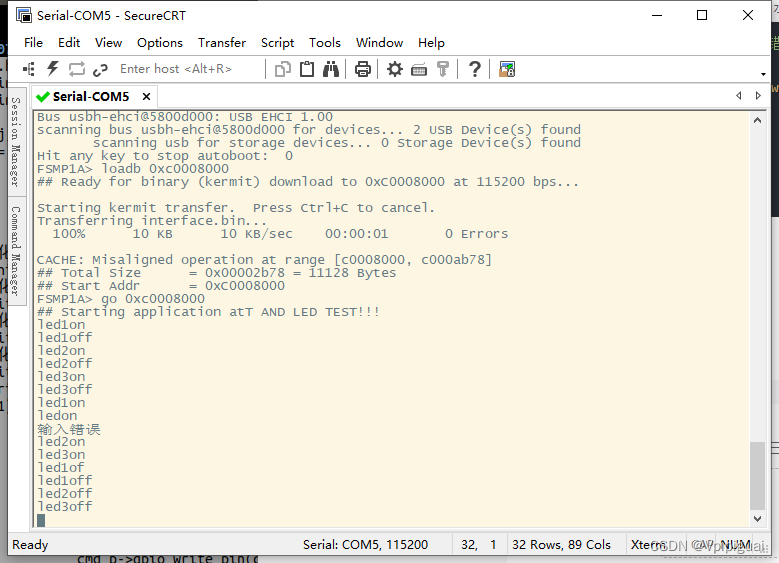
通过操作Cortex-A7核，串口输入相应的命令，控制LED灯进行工作

1.通过操作Cortex-A7核&#xff0c;串口输入相应的命令&#xff0c;控制LED灯进行工作 例如在串口输入led1on,开饭led1灯点亮 2.例如在串口输入led1off,开饭led1灯熄灭 3.例如在串口输入led2on,开饭led2灯点亮 4.例如在串口输入led2off,开饭led2灯熄灭 5.例如在串口输入led…...

编程日记 2023/3/15 23:57:36

Python实现某du文库vip内容下载，保存成PDF

前言 是谁&#xff0c;是谁在网页上搜索往年考试卷题答案的时候只能阅读前两页的选择题&#xff0c;是谁在搜几千字的文档资料只能看25%&#xff0c;是谁在百度文库找七找八的时候所有的东西都要付费才能继续看… 我先说 是我自己 我又不经常用&#xff0c;只有偶尔需要看看…...

编程日记 2023/3/15 12:41:37

vue3.0 模板语法

文章目录前言&#xff1a;1. 内容渲染指令1.1 v-text1.2 {{ }}插值表达式1.3 v-html2. 双向绑定指令2.1 v-model2.2 v-model的修饰符3. 属性绑定指令3.1 动态绑定多个属性值3.2 绑定class和style属性4.条件渲染指令4.1 v-if、v-else-if、v-else4.2 v-show4.3 v-if与v-show的区别…...

编程日记 2023/3/15 12:44:44

【GlobalMapper精品教程】054：标签（标注）功能案例详解

同ArcGIS标注一样，globalmapper提供了动态标注的功能，称为标签，本文详解标签的使用方法。 文章目录 一、标签配置二、创建标签图层三、标签图层选项1. 标签字段2. 标签样式3. 标签格式4. 标签语言5. 标签优先级一、标签配置 在配置页面的【矢量显示】→标签选项卡下，有标签…...

编程日记 2023/3/15 23:58:45

超详细树状数组讲解（+例题：动态求连续区间和）

树状数组的作用&#xff1a;快速的对数列的一段范围求和快速的修改数列的某一个数为什么要使用树状数组&#xff1a;大家从作用中看到快速求和的时候可能会想到为什么不使用前缀和只需要预处理一下就可以在O(1)的时间复杂度下实行对于数列的一段范围的和但是我们可以得到当我们…...

编程日记 2023/2/25 10:38:40

【学习笔记】AGC055

A - ABC Identity 如果只有AAA,BBB两种字符的话&#xff0c;我们发现要寻找p∈[1,n]p\in [1,n]p∈[1,n]&#xff0c;使得[1:p][1:p][1:p]中AAA的数目与[p1:n][p1:n][p1:n]中BBB的数目相同。 如果有A,B,CA,B,CA,B,C三种字符&#xff0c;我们可以先将A,BA,BA,B分离出来&#xf…...

编程日记 2023/3/17 6:31:29

墨者——内部文件上传系统漏洞分析溯源 内部文件上传系统漏洞分析溯源

墨者——内部文件上传系统漏洞分析溯源 内部文件上传系统漏洞分析溯源 1.选择合适的文件上传 2.可以看到为*.asp文件 3.可以推测出此站点为IIS 4.上传shell.asp试试 5.上传报错&#xff0c;将其改名为shell.asp.txt上传&#xff0c;发现上传成功 6.有个问题就是服务器将我们所…...

编程日记 2023/3/16 7:57:05

5.2 Python if语句

5.2.3 检查是否不相等要判断两个值是否不等&#xff0c;可结合使用惊叹号和等号(!)&#xff0c;其中的惊叹号表示不&#xff0c;在很多编程语言中都如此。下面再使用一条if语句来演示如何使用不等运算符。我们将把要求的比萨配料存储在一个变量中&#xff0c;再打印一条消息&am…...

编程日记 2023/3/16 16:13:15

ubuntu gerrit 配置

1 - 简介 参考地址： https://www.cnblogs.com/anliven/p/12019974.html https://www.cnblogs.com/anliven/p/11980432.html 虽然Gerrit 本身提供 Code Review和 Git 仓库的两大功能，但实际上很多项目用的是其他的Git仓库，例如GitLab和GitHub。 一般情况下，Gerrit位于最终…...

编程日记 2023/4/1 3:03:15

运动蓝牙耳机什么牌子好，运动蓝牙耳机品牌推荐

现在市面上运动耳机的品牌越来越多&#xff0c;还不知道选择哪一些运动耳机品牌&#xff0c;可以看看下面的一些耳机分享&#xff0c;运动耳机需要注意耳机的参数配置以及佩戴舒适度&#xff0c;根据自己最根本的使用需求来选择运动耳机。 1、南卡Runner Pro4骨传导蓝牙运动耳…...

编程日记 2023/4/1 3:05:07

(7)C#传智：方法及参数、重载(第7天)

一、方法作用域 被调用者需要调用者的值,方法有二: 1.传参数. private static void Main(string[] args){int m 3;Console.WriteLine(m);Console.ReadKey();}public static int GetMax(int m){return m 3;} 2.使用静态字段模拟全局. 多个方法都需要时&#x…...

编程日记 2023/3/21 11:34:58

Python 函数式编程

函数式编程&#xff1a;允许把函数本身作为参数传入另一个函数&#xff0c;还允许返回一个函数&#xff01; 1.高阶函数 一个函数可以接收另一个函数作为参数&#xff0c;这种函数称之为高阶函数 abs(-10) 是函数调用 abs是函数本身 abs函数名其实是一个变量名 变量可以…...

编程日记 2023/3/15 12:49:37

pandas读取EXCEL列名重复问题解决——pandas设置多行为列名（多层列名）

问题呈现 这是我在问答区看到的一个问题。 问&#xff1a;在python中使用pandas读取Excel数据&#xff0c;重复数据被区分了&#xff0c;如何做到重复数据不被区分&#xff1f; 解决思路 很明显&#xff0c;这是pandas读取excel文件时列名设置问题&#xff0c;我第一时间想…...

编程日记 2023/3/20 11:15:55