排序算法-基数排序法(RadixSort)
排序算法-基数排序法(RadixSort)
1、说明
基数排序法与我们之前讨论的排序法不太一样,并不需要进行元素之间的比较操作,而是属于一种分配模式排序方式。
基数排序法比较的方向可分为最高位优先(Most Significant Digit First,MSD)和最低位优先(Least Significant Digit First,LSD)两种。MSD是从最左边的位数开始比较的,而LSD则是从最右边的位数开始比较的。
2、算法分析
- 在所有情况下,时间复杂度均为
,k是原始数据的最大值。
- 基数排序法是稳定排序法。
- 基数排序法要使用很大的额外空间来存放列表数据,其空间复杂度为
,n是原始数据的个数,p是数据字符数。
- 若n很大,p固定或很小,则此排序法的效率很高。
3、C++代码
#include<iostream>
#include<iomanip>
using namespace std;void PrintData(int data[], int size) {for (int i = 0; i < size; i++) {cout << data[i] << " ";}cout << endl;
}void SetData(int data[], int size) {srand(time(nullptr));for (int i = 0; i < size; i++) {data[i] = rand() % 999 + 1;}
}void Radix(int data[], int size) {for (int n = 1; n <= 100; n *= 10) {int temp[10][100] = { 0 };for (int i = 0; i < size; i++) {int m = (data[i] / n) % 10;temp[m][i] = data[i];}int k = 0;for (int i = 0; i < 10; i++) {for (int j = 0; j < size; j++) {if (temp[i][j] != 0) {data[k] = temp[i][j];k++;}}}cout << "经过" << setw(3) << n << "位排序后:";PrintData(data, size);}
}int main() {int size = 20;int* data = new int[size];SetData(data, size);cout << "原始数据:";PrintData(data, size);cout << "---------------------------------" << endl;Radix(data, size);cout << "---------------------------------" << endl;cout << "最终数据:";PrintData(data, size);return 0;
}输出结果
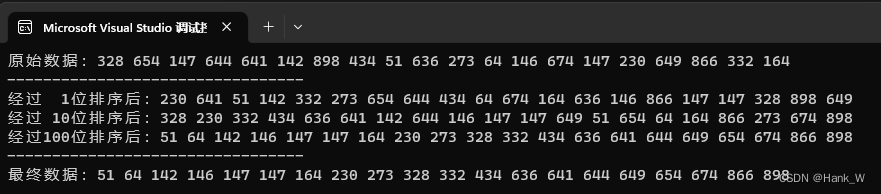
相关文章:

排序算法-基数排序法(RadixSort)
排序算法-基数排序法(RadixSort) 1、说明 基数排序法与我们之前讨论的排序法不太一样,并不需要进行元素之间的比较操作,而是属于一种分配模式排序方式。 基数排序法比较的方向可分为最高位优先(Most Significant Di…...

nginx绑定tomcat与tomcat联合使用的配置(nginx反向代理tomcat的配置说明)
nginx反向代理tomcat通信配置 (内容来自网上,注解部分才是原创) 切记: url的意思就是 unifed resource location 统一资源定位 其中location就是定位的意思 所以上文中的location就有 对应匹配的 url 标识的资源的相关配置之…...
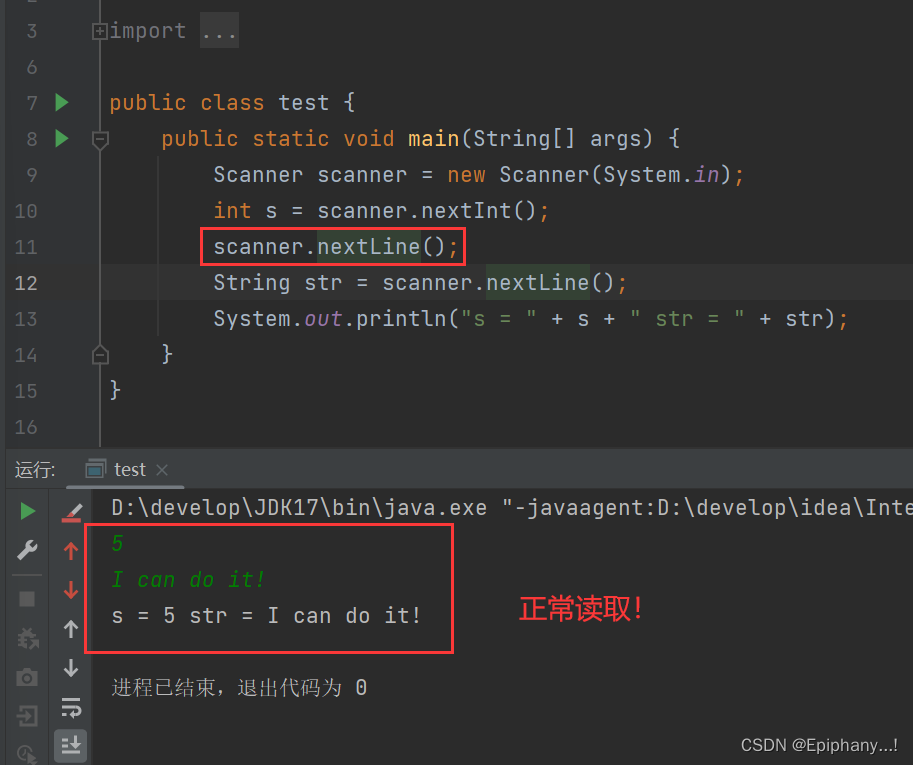
【Java】nextInt()后面紧接nextLine()读取不到数据/InputMismatchException异常的解决方案
错误如下: 有时候还会抛出InputMismatchException异常 看!我只输入了一个5,并没有给str赋值,它就已经将结果打印出来了!这就意味着,str是读取到了数据的,只不过这个数据并不是我们想要的输入的…...
【传输层协议】UDP/TCP结构特点与原理(详解)
文章目录 1. UDP1.1 UDP结构1.2 UDP特点1. 无连接2. 不可靠3. 面向数据报4. 缓冲区5. 大小受限6. 无序性 2. TCP2.1 TCP结构2.2 TCP特点1. 有连接2. 可靠性3. 面向字节流4. 拥塞控制5. 头部开销 2.3 TCP原理1. 确认应答(安全机制)2. 超时重传(…...

哪种网站适合物理服务器
哪种网站适合物理服务器 看到独立服务器这一词语,相信大家脑海立马就浮现出了它的种种优势,但是有优势就伴随着也有一定的弊端,比如说它的空间大、特殊的的组件配置,权限配置等,但是成本却非常的高,那么我…...

uni-app集成使用SQLite
一、打开uni-app中SQLite 二、封装sqlite.js module.exports {dbName: chat, // 数据库名称dbPath: _doc/chat.db, // 数据库地址,推荐以下划线为开头 _doc/xxx.db/*** Description: 创建数据库 或 有该数据库就打开* author: ZXL* createTime: 2023-10-12 09:23:10* Copyr…...

Qt不能安装自己想要的版本,如Qt 5.15.2
使用在线安装工具安装Qt5.15.2时,发现没有Qt 5的相关版本,只有Qt 6的版本,这时选择右边的Archive,再点击筛选,这时就会出现之前的Qt版本。...
学信息系统项目管理师第4版系列28_组织级项目管理和量化项目管理
1. OPM 1.1. 旨在确保组织开展正确项目并合适地分配关键资源 1.1.1. 有助于确保组织的各个层级都了解组织的战略愿景、实现愿景的措施、组织目标以及可交付成果 1.2. 业务评估是建立OPM框架的必要组件 1.3. OPM3 是组织级项目管理成熟度模型,可用于评估组织项目…...

Bean实例化的三级缓存
在Spring框架中,Bean实例化的三级缓存(三级缓存也称为三级缓存机制)是用于缓存Bean定义的一种机制,用于管理和加速Spring容器中Bean的创建和初始化过程。三级缓存包括了singletonObjects、earlySingletonObjects 和 singletonFact…...

Jenkins+Gitlab+Docker(Dockerfile)部署
Docker部署运行 上一篇内容中使用Jenkins(运行服务器)Gitlab(代码存储库)Webhook(网络钩子)的方式部署运行我们的项目。需要我们在服务器上做好很多相关的环境配置及依赖。 那么假如有这样一个场景:需要把不同技术栈的项目部署到同一台服务器上运行。比如PH…...
)
Web前端-Vue2+Vue3基础入门到实战项目-Day4(组件的三大组成部分, 组件通信, 案例-组件版小黑记事本, 进阶语法)
Web前端-Vue2Vue3基础入门到实战项目-Day4 组件的三大组成部分(结构/样式/逻辑)scoped样式冲突data是一个函数 组件通信组件通信语法父传子子传父props详解什么是propsprops检验props与data的区别 非父子(扩展)事件总线 (event bus)provide - inject 案例 - 小黑记事本(组件版)…...
【大模型应用开发教程】01_大模型简介
C1 大模型简介 一. 什么是LLM(大语言模型)?1. 发展历程2. 大语言模型的概念LLM的应用和影响 二、大模型的能力和特点1. 大模型的能力1.1 涌现能力(emergent abilities)1.2 作为基座模型支持多元应用的能力1.3 支持对话…...

Flume 简介及基本使用
1.Flume简介 Apache Flume 是一个分布式,高可用的数据收集系统。它可以从不同的数据源收集数据,经过聚合后发送到存储系统中,通常用于日志数据的收集。Flume 分为 NG 和 OG (1.0 之前) 两个版本,NG 在 OG 的基础上进行了完全的重构…...
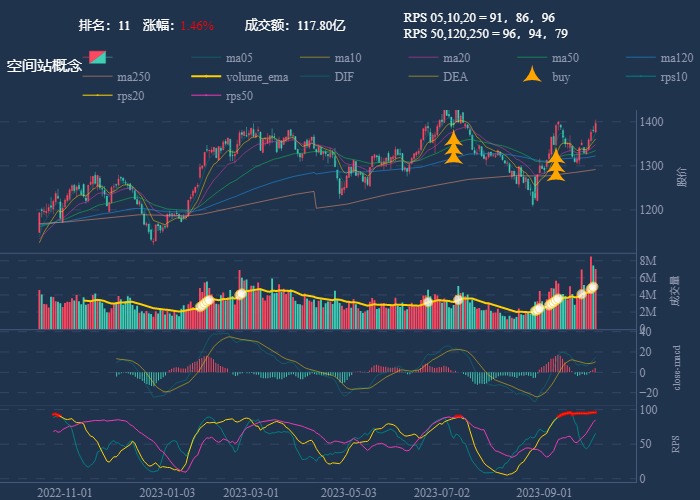
行业追踪,2023-10-11
自动复盘 2023-10-11 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...
Linux:进程控制
目录 一、进程创建 写时拷贝 二、进程终止 echo $? 如何终止进程 _exit与exit 三、进程等待 进程等待的必要性 进程等待的操作 wait waitpid status 异常退出情况 status相关宏 options 四、进程程序替换 1、关于进程程序替换 2、如何进行进程程序替换 程序…...

HTTP中的GET方法与POST方法
1、GET 和 POST方法之间的区别 根据 RFC 规范,GET 的语义是从服务器获取指定的资源,这个资源可以是静态的文本、页面、图片视频等。GET 请求的参数位置一般是写在 URL 中,URL 规定只能支持 ASCII,所以 GET 请求的参数只允许 ASCI…...
)
2023年10月16日-10月22日,(光追+ue+osg继续按部就班进行即可。)
根据月计划, 本周计划如下: 2023年10月16日-10月22日,光追10.7-10.13,ue rpg(p47-p53),ue5底层渲染01A19-01B4,osg29,osg30,filament文档每天看 落实到天就是 2023年10月16日光追10.7,ue rpg(p47),ue5底层渲染01A19,o…...

【Docker】命令使用大全
【Docker】命令使用大全 目录 【Docker】命令使用大全 简述 Docker 的主要用途 基本概念 容器周期管理 run start/stop/restart kill rm pause/unpause create exec 容器操作 ps inspect top attach events logs wait export port 容器 rootfs 命令 c…...

查找算法:二分查找、插值查找、斐波那契查找
二分查找 查找的前提是数组有序 思路分析 代码实现 # 二分查找(递归法实现) # 找到一个相等的值就返回该值的下标 def binary_search(arr: list, find_val: int, left: int, right: int):mid (left right) // 2 # 寻找数组中间位置的下标if left &…...
python+django高校教室资源预约管理系统lqg8u
技术栈 后端:pythondjango 前端:vueCSSJavaScriptjQueryelementui 开发语言:Python 框架:django/flask Python版本:python3.7.7 数据库:mysql 数据库工具:Navicat 开发软件:PyChar…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
