Elucidating the Design Space of Diffusion-Based Generative Models 阅读笔记
文章使用模块化(modular)的思想,分别从采样、训练、score network设计三个方面分析和改进diffusion-based models。
之前的工作1已经把diffusion-based models统一到SDE或者ODE框架下了,这篇文章的作者同样也从SDE和ODE的角度出发,不过换了一种SDE和ODE的表示形式。
假设有方差是 σ d a t a \sigma_{data} σdata的数据分布 p d a t a ( x ) p_{data}(\mathbf x) pdata(x)。考虑一族分布 p ( x ; σ ) p(\mathbf x; \sigma) p(x;σ),其通过对数据添加方差为 σ \sigma σ的高斯噪声产生。在变化的过程中加入缩放 x = s ( t ) x ^ \mathbf x=s(t)\hat{\mathbf x} x=s(t)x^,则有下面的ODE:
d x = [ s ˙ ( t ) s ( t ) x − s ( t ) 2 σ ˙ ( t ) σ ( t ) ∇ x log p ( x s ( t ) ; σ ( t ) ) ] d t (4) \mathrm{d} \mathbf x = \left[ \frac{\dot s(t)}{s(t)} \mathbf x - s(t)^2 \dot\sigma(t) \sigma(t) \nabla_{\mathbf x} \log p(\frac{\mathbf x}{s(t)}; \sigma(t)) \right] dt \tag{4} dx=[s(t)s˙(t)x−s(t)2σ˙(t)σ(t)∇xlogp(s(t)x;σ(t))]dt(4)perturbation kernel的形式是:
p 0 t ( x ( t ) ∣ x ( 0 ) ) = N ( x ( t ) ; s ( t ) x ( 0 ) , s ( t ) 2 σ ( t ) 2 I ) (11) p_{0t}(\mathbf x(t) | \mathbf x(0)) = \mathcal N(\mathbf x(t) ; s(t)\mathbf x(0), s(t)^2\sigma(t)^2 \mathbf I) \tag{11} p0t(x(t)∣x(0))=N(x(t);s(t)x(0),s(t)2σ(t)2I)(11)在之前的工作1中SDE的形式是:
d x = f ( t ) x + g ( t ) d w t (10) \mathrm{d} \mathbf x = f(t)\mathbf x + g(t)dw_t \tag{10} dx=f(t)x+g(t)dwt(10)其中 s ( t ) = exp ( ∫ o t f ( ξ ) d ξ ) s(t)=\exp(\int_o^t f(\xi)d\xi) s(t)=exp(∫otf(ξ)dξ), σ ( t ) = ∫ o t g ( ξ ) 2 s ( ξ ) 2 d ξ \sigma(t)=\sqrt{\int_o^t \frac{g(\xi)^2}{s(\xi)^2}d\xi} σ(t)=∫ots(ξ)2g(ξ)2dξ。
不同于之前的论文,这篇文章考虑的是一个直接估计去噪输出的去噪函数 D ( x ; σ ) D(\mathbf x;\sigma) D(x;σ)。
E y ∼ p d a t a E n ∼ N ( 0 , σ 2 I ) ∥ D ( y + n ; σ ) − y ∥ 2 2 , ∇ x log p ( x ; σ ) = ( D ( x ; σ ) − x ) / σ 2 (2,3) \mathbb E_{y \sim p_{data}} \mathbb E_{\mathbf n \sim \mathcal N(\mathbf 0, \sigma^2 \mathbf I)} \| D(\mathbf y + \mathbf n;\sigma) - \mathbf y \|_2^2,~~~~\nabla_{\mathbf x}\log p(\mathbf x ; \sigma) = (D(\mathbf x; \sigma) - \mathbf x)/ \sigma^2 \tag{2,3} Ey∼pdataEn∼N(0,σ2I)∥D(y+n;σ)−y∥22, ∇xlogp(x;σ)=(D(x;σ)−x)/σ2(2,3)其中 y \mathbf y y是训练样本, n \mathbf n n是添加的噪声。在这种设置下,score function变成了用 D ( x ; σ ) D(\mathbf x;\sigma) D(x;σ)估计添加的噪声。用网络 D θ ( x ; σ ) D_\theta(\mathbf x;\sigma) Dθ(x;σ)按照公式(2)可以估计 D ( x ; σ ) D(\mathbf x;\sigma) D(x;σ)。需要注意的是, D θ ( x ; σ ) D_\theta(\mathbf x;\sigma) Dθ(x;σ)可能包括额外的预处理步骤和后处理步骤。
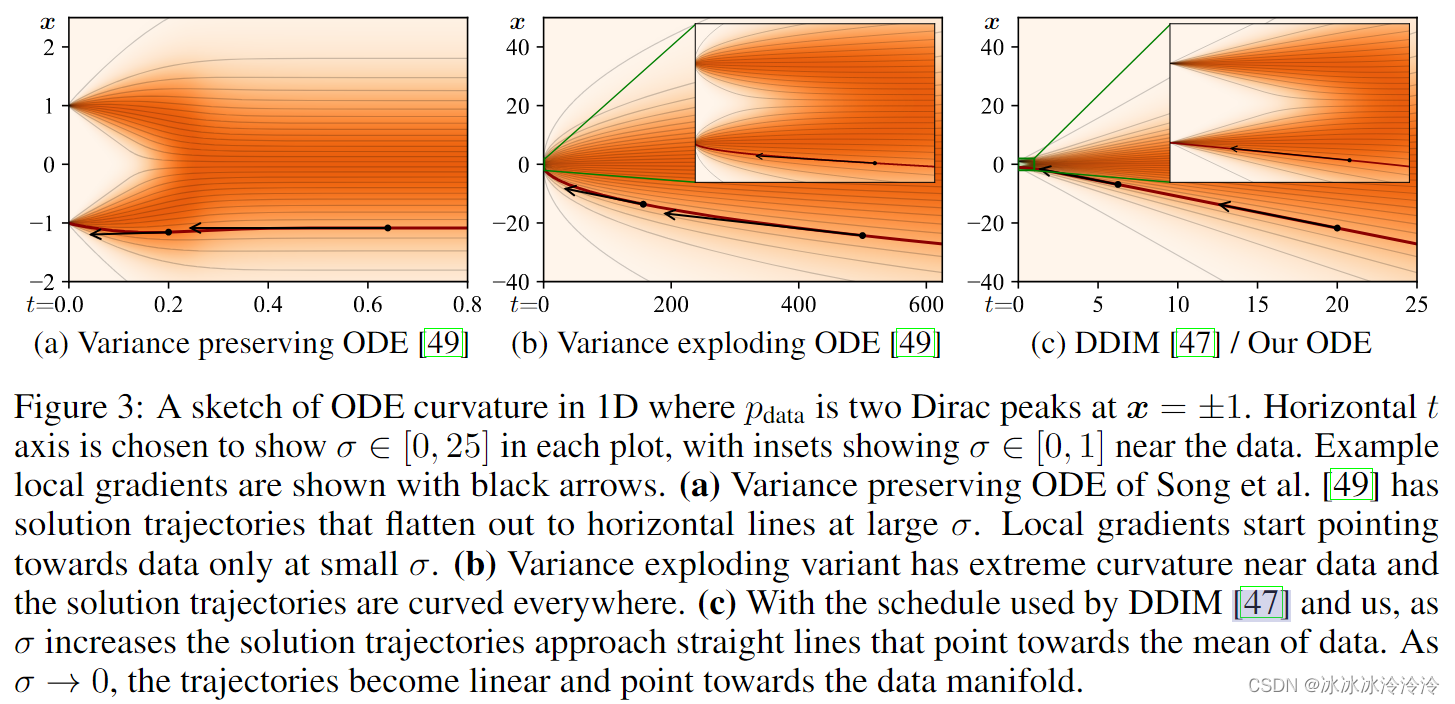
ODE解轨迹的形状由 σ ( t ) \sigma(t) σ(t)和 s ( t ) s(t) s(t)决定。因为在求解微分方程的时候截断误差(truncation error)和 d x / d t dx/dt dx/dt的曲率有关,作者认为最好的选择是 σ ( t ) = t \sigma(t)=t σ(t)=t和 s ( t ) = 1 s(t)=1 s(t)=1,这样 d x / d t = ( x − D ( x ; t ) ) / t dx/dt=(\mathbf x-D(\mathbf x;t))/t dx/dt=(x−D(x;t))/t,并且 σ \sigma σ和 t t t是相同的,两个符号可以串着用。好处是在任何 x , t x,t x,t位置,一个到 t = 0 t=0 t=0的Euler步就是对去噪图像的估计 D θ ( x ; t ) D_\theta(\mathbf x;t) Dθ(x;t),解估计的切线总是指向去噪图像。如下图所示(c)也就是 σ ( t ) = t \sigma(t)=t σ(t)=t和 s ( t ) = 1 s(t)=1 s(t)=1的情况,这和DDIM相同。
SDE可以表示成:
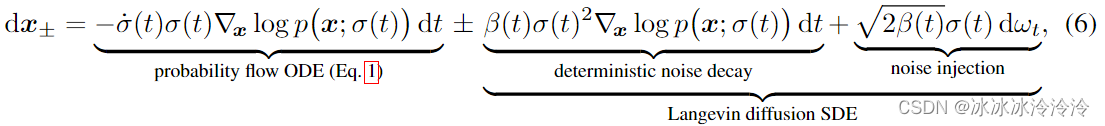
这揭示了为什么随机性在实践中有帮助:隐式朗之万扩散驱动样本在给定时间朝向所需的边际分布,主动纠正早期采样步骤中产生的任何错误。
直接用网络 D θ D_\theta Dθ预测 D ( x ; σ ) D(\mathbf x;\sigma) D(x;σ)在实践中效果并不好,作者考虑对网络 F θ F_\theta Fθ添加预处理步骤和后处理步骤来预测 D ( x ; σ ) D(\mathbf x;\sigma) D(x;σ)
D θ ( x ; σ ) = c s k i p ( σ ) x + c o u t ( σ ) F θ ( c i n ( σ ) x ; c n o i s e ( σ ) ) D_\theta(\mathbf x;\sigma)=c_{skip}(\sigma) \mathbf x + c_{out}(\sigma) F_\theta(c_{in}(\sigma)\mathbf x; c_{noise}(\sigma)) Dθ(x;σ)=cskip(σ)x+cout(σ)Fθ(cin(σ)x;cnoise(σ))

Score-Based Generative Modeling through Stochastic Differential Equations ↩︎ ↩︎
相关文章:

Elucidating the Design Space of Diffusion-Based Generative Models 阅读笔记
文章使用模块化(modular)的思想,分别从采样、训练、score network设计三个方面分析和改进diffusion-based models。 之前的工作1已经把diffusion-based models统一到SDE或者ODE框架下了,这篇文章的作者同样也从SDE和ODE的角度出发…...
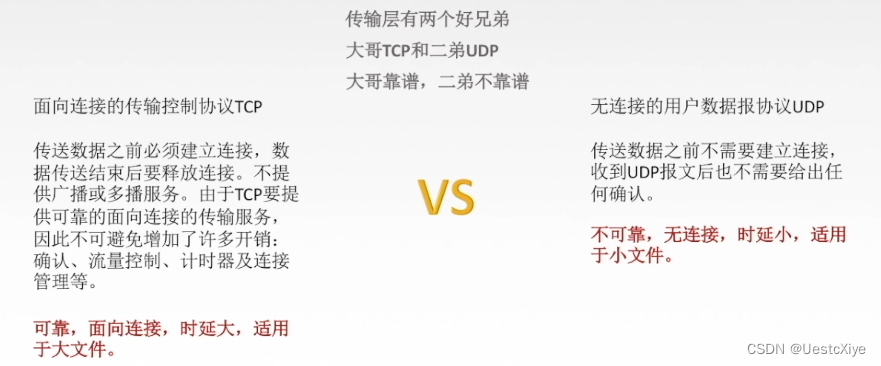
计算机网络 | 传输层
计算机网络 | 传输层 计算机网络 | 传输层功能概述 参考视频:王道计算机考研 计算机网络 参考书:《2022年计算机网络考研复习指导》 计算机网络 | 传输层 功能概述 传输层是主机才有的层次。 复用:发送方的不同应用进程都可以使用同一个传…...

Android 13 隐私权限和安全变更之通知
介绍 根据官网https://developer.android.com/about/versions/13/summary?hlzh-cn展示的Android 13 功能和变更列表中提及的,Android 13(API 级别 33)引入了新的权限POST_NOTIFICATIONS。 使用 在Android 13及以上版本,如需向…...
)
docker-compose安装和使用(自启、redis、mysql、rabbitmq、activemq、es、nginx、java应用)
1.在线安装docker-compose: 参考官网:https://docs.docker.com/compose/install/other/ docker-compose安装及简单入门 [Docker] docker-compose使用教程 Docker系列教程22-docker-compose.yml常用命令 # 安装(加速下载https://ghproxy.…...

dll文件缺失,ps,pr无法打开,游戏运行不了如何解决
最近重装了系统,然后打开原来的软件发现都会报错,说***.dll文件缺失 于是找了很多解决办法 方案一 说是下载一个dll文件恢复助手,一键恢复 不要信 统统不管用,不是收费高就是没作用 方案二 下载对应dll文件去c盘对应软件位置…...
前后端数据导入导出Excel
一:导入 Excel有读取也便有写出,Hutool针对将数据写出到Excel做了封装。 原理 Hutool将Excel写出封装为ExcelWriter,原理为包装了Workbook对象,每次调用merge(合并单元格)或者write(写出数据&…...

RackNerd 圣何塞 VPS 测评
发布于 2023-07-06 on https://chenhaotian.top/vps/racknerd-ca/ RackNerd 圣何塞 VPS 测评 官网链接:https://my.racknerd.com/index.php?rp/store/kvm-vps 这款是2022年双十一特别款,现在已经买不到了 网络是G口,4T流量 稳定性不错&…...
php74 安装sodium
下载编译安装libsodium wget https://download.libsodium.org/libsodium/releases/libsodium-1.0.18-stable.tar.gz tar -zxf libsodium-1.0.18-stable.tar.gz cd libsodium-stable ./configure --without-libsodium make && make check sudo make install下载编译安装…...

优思学院:想成为质量工程师?了解质量工程师职责和能力是关键!
在职场中,质量工程师的角色显得至关重要。但如果你不清楚质量工程师的工作职责以及所需具备的能力,那么这个岗位可能会显得遥不可及。本文将为你详细介绍质量工程师的工作内容以及如何选择适合自己的质量工程师岗位。 一、质量工程师的工作职责 1. 质量…...
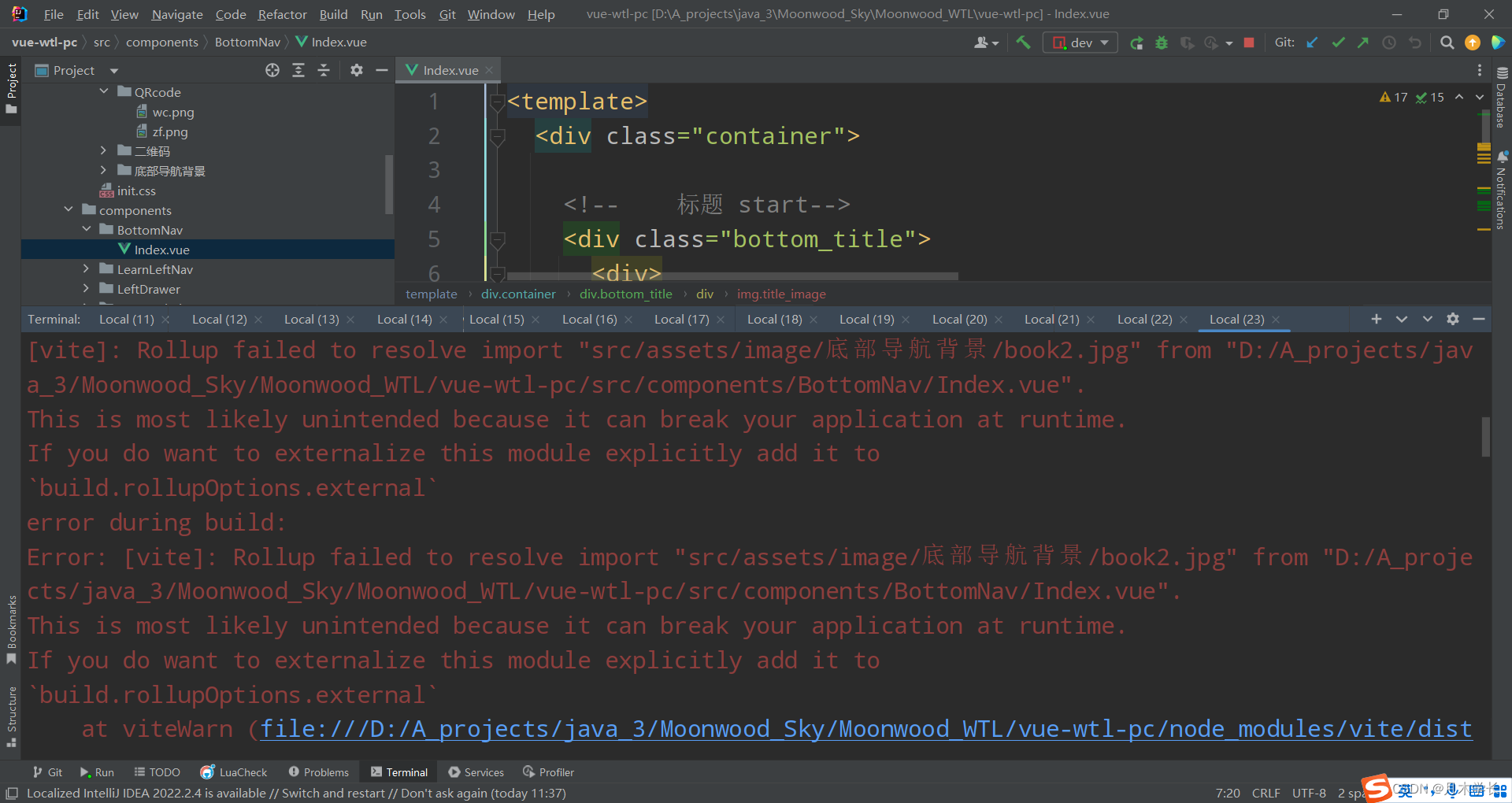
Rollup failed to resolve import
问题描述 我在打包vue3的项目的时候报了以下错误 问题原因 打包时,静态资源目录没有识别出来,导致打包终止并报错 问题解决 需要把路径改为跟路径,就可以打包啦 错误资源路径写法 <img src"src/assets/image/底部导航背景/book2…...

基于VScode 使用plantUML 插件设计状态机
本文主要记录本人初次在VScode上使用PlantUML设计 本文只讲述操作的实际方法,假设java已安装成功 。 1. 在VScode下安装如下插件 2. 验证环境是否正常 新建一个文件夹并在目录下面新建文件test.plantuml 其内容如下所示: startuml hello world skinparam Style …...
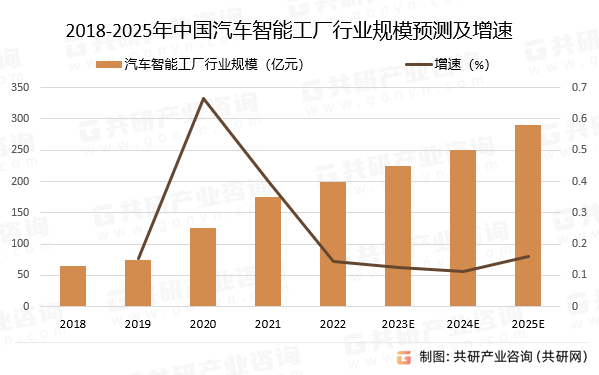
2023年中国汽车智能工厂市场规模不断增大,智能化已成趋势[图]
汽车智能工厂是在数字化工厂的基础上,通过互联网技术与工业技术结合,数据监管设备以及AI等技术的结合,实现汽车整车从原材料及零部件的生产到运输、组装一系列的自动化生产。汽车智能工厂很大程度上降低成本和人为干扰,实现自动化…...

cola架构:一种扩展点的实现思路浅析
目录 1.扩展点使用实例 2.主要技术点 2.1 注解加持 2.2 注解解析 2.3 扩展点路由 在实际项目中,我们经常使用策略模式、或者状态模式来隔离同一接口下不同的实现逻辑,进而消除代码中ifelse硬编码分支,使代码结构更清晰,也大大…...

Thread常用API
setname方法每个线程取名 需要创建构造器 线程设置名字 package Thread_api_test;// 继承Thread类 public class MyThread extends Thread {//创建构造器 线程设置名字public MyThread(String name){super(name);}Overridepublic void run() {super.run();Thread mThread.cur…...
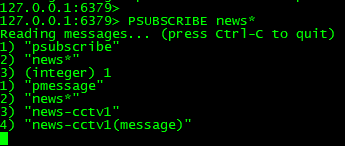
系列九、Redis的发布订阅
一、概述 Redis的发布订阅是进程间的一种消息通信模式,发送者(Publisher)发送消息,订阅者(Subscriber)接收消息。 二、命令 三、案例演示 3.1、订阅单个 客户端订阅 cctv-1、cctv-2、 cctv-3三个频道 SUB…...

《TypeScript》系列之对比JavaScript,TypeScript的优势
概述 TypeScript是微软公司开发的一种基于JavaScript语言的编程语言,它的目的并不是创造一种全新的语言,而是增强JavaScript的功能,使其更适合多人合作的企业级项目。TypeScript可以看做是JavaScript的超集,即它继承了后者的全部…...
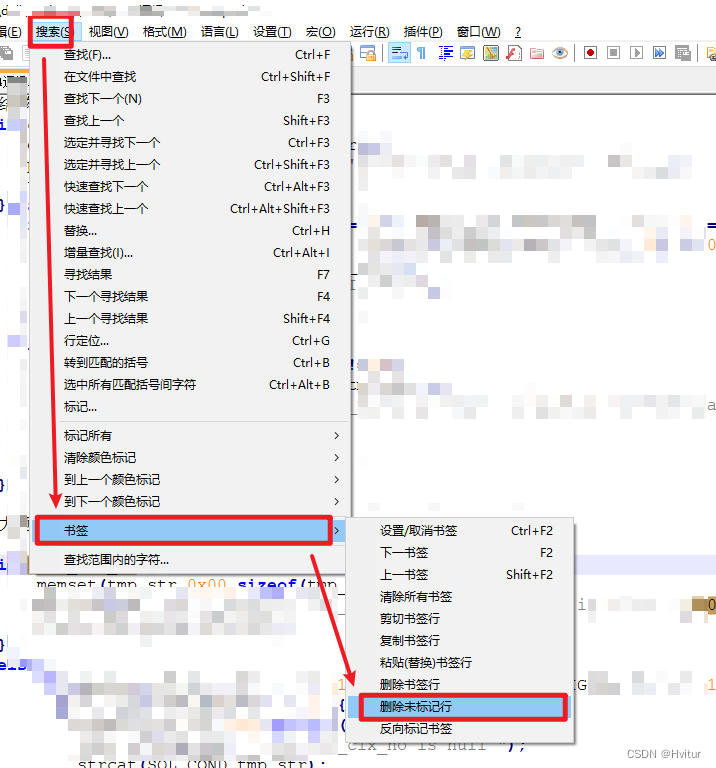
Notepad++使用技巧
显示远程连接的文件目录 自动完成:函数自动提示 自动输入:输入一半括号自动补全另一半 自动关联 .pc文件识别为C 列模式 按住Alt不松手,可以直接范围选择,便于编辑选择的区域 关键行筛选 1.进入搜索页面的标记 2.选中标…...
)
React 中报Type error: Could not find a declaration file for module ‘qs‘.(已解决)
ts项目引入qs 比如 nextjs 或者reactjs npm install --save-dev types/qs 确保你的tsconfig.json文件中有以下设置 {"compilerOptions": {"types": ["qs"]}} 如果你的项目中没有tsconfig.json文件,你可以创建一个。在项目根目录下创…...

【Linux】:Linux环境与版本
以下哪个命令输出Linux内核的版本信息 A.uname -r B.vmstat C.sar D.stat uname -r 查看linux内核版本信息 vmstat 报告关于内核线程、虚拟内存、磁盘、陷阱和 CPU 活动的统计信息 sar 主要帮助我们掌握系统资源的使用情况,特别是内存和CPU的使用情况 stat 用于显示…...

PNG转EPS,包括Latex导入
在电脑TEXLIVE文件夹里中找到bmeps.exe TEXLIVE\2022\bin\win32 可以新建一个文件夹picture(图片和exe文件必须在一个文件夹里),将bmeps.exe复制出来,方便后续大量图片操作 导入png图片 新建一个txt文件,命名为Fig1.…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
