数据结构预算法之买股票最好时机动态规划(可买卖多次)
一.题目

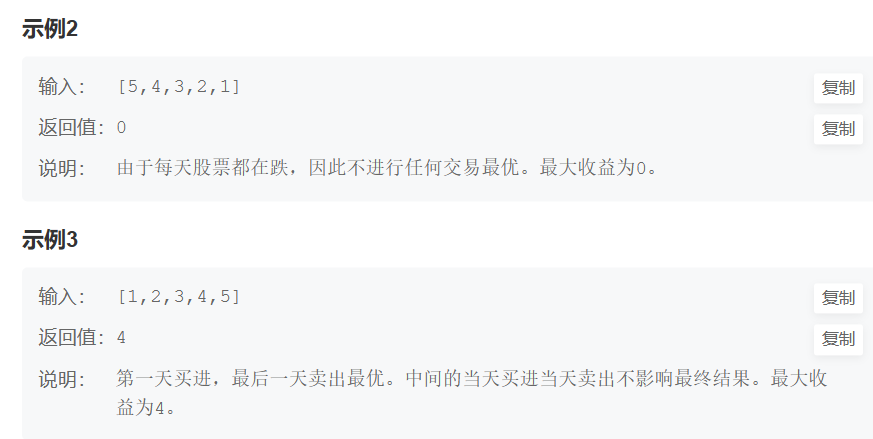

二.思路
在动规五部曲中,这个区别主要是体现在递推公式上,其他都和上一篇文章思路是一样的。
所以我们重点讲一讲递推公式。
这里重申一下dp数组的含义:
dp[i][0] 表示第i天持有股票所得现金。
dp[i][1] 表示第i天不持有股票所得最多现金
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
第i天买入股票,所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即:dp[i - 1][1] - prices[i]
注意这里和上一题唯一不同的地方,就是推导dp[i][0]的时候,第i天买入股票的情况。
在上一题中,因为股票全程只能买卖一次,所以如果买入股票,那么第i天持有股票即dp[i][0]一定就是 -prices[i]。
而本题,因为一只股票可以买卖多次,所以当第i天买入股票的时候,所持有的现金可能有之前买卖过的利润。
那么第i天持有股票即dp[i][0],如果是第i天买入股票,所得现金就是昨天不持有股票的所得现金 减去 今天的股票价格 即:dp[i - 1][1] - prices[i]。
再来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices[i] + dp[i - 1][0]
注意这里和上一题就是一样的逻辑,卖出股票收获利润(可能是负值)天经地义!
C++代码如下:
(注意代码中的注释,标记了和121.买卖股票的最佳时机唯一不同的地方)
class Solution {
public:int maxProfit(vector<int>& prices) {int len = prices.size();vector<vector<int>> dp(len, vector<int>(2, 0));dp[0][0] -= prices[0];dp[0][1] = 0;for (int i = 1; i < len; i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[len - 1][1];}
};时间复杂度:O(n)
空间复杂度:O(n)
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);这正是因为本题的股票可以买卖多次! 所以买入股票的时候,可能会有之前买卖的利润即:dp[i - 1][1],所以dp[i - 1][1] - prices[i]。
想到到这一点,对这两道题理解的就比较深刻了。
Java语言版本:
// 动态规划
class Solution // 实现1:二维数组存储// 可以将每天持有与否的情况分别用 dp[i][0] 和 dp[i][1] 来进行存储// 时间复杂度:O(n),空间复杂度:O(n)public int maxProfit(int[] prices) {int n = prices.length;int[][] dp = new int[n][2]; // 创建二维数组存储状态dp[0][0] = 0; // 初始状态dp[0][1] = -prices[0];for (int i = 1; i < n; ++i) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]); // 第 i 天,没有股票dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]); // 第 i 天,持有股票}return dp[n - 1][0]; // 卖出股票收益高于持有股票收益,因此取[0]}
}相关文章:

数据结构预算法之买股票最好时机动态规划(可买卖多次)
一.题目二.思路在动规五部曲中,这个区别主要是体现在递推公式上,其他都和上一篇文章思路是一样的。所以我们重点讲一讲递推公式。这里重申一下dp数组的含义:dp[i][0] 表示第i天持有股票所得现金。dp[i][1] 表示第i天不持有股票所得最多现金如…...
)
华为OD机试真题Java实现【蛇形矩阵】真题+解题思路+代码(20222023)
蛇形矩阵 蛇形矩阵是由1开始的自然数依次排列成的一个矩阵上三角形。 例如,当输入5时,应该输出的三角形为: 1 3 6 10 15 2 5 9 14 4 8 13 7 12 11请注意本题含有多组样例输入。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Java)真题目录汇总 输入描述:…...
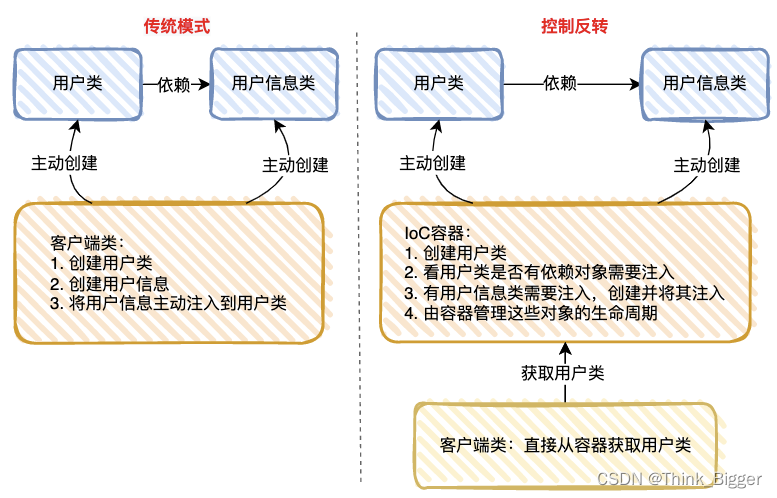
spring Bean的生命周期 IOC
文章目录 1. 基础知识1.1 什么是 IoC ?2. 扩展方法3. 源码入口1. 基础知识 1.1 什么是 IoC ? IoC,控制反转,想必大家都知道,所谓的控制反转,就是把 new 对象的权利交给容器,所有的对象都被容器控制,这就叫所谓的控制反转。 IoC 很好地体现了面向对象设计法则之一 —…...

详解cors跨域
文章目录同源策略cors基本概念cors跨域方式简单请求 simple request非简单请求- 预检请求CORS兼容情况CORS总结同源策略 在以前的一篇博客中有介绍,同源策略是一种安全机制,为了预防某些恶意的行为,限制浏览器从不同源文档和脚本进行交互的行…...
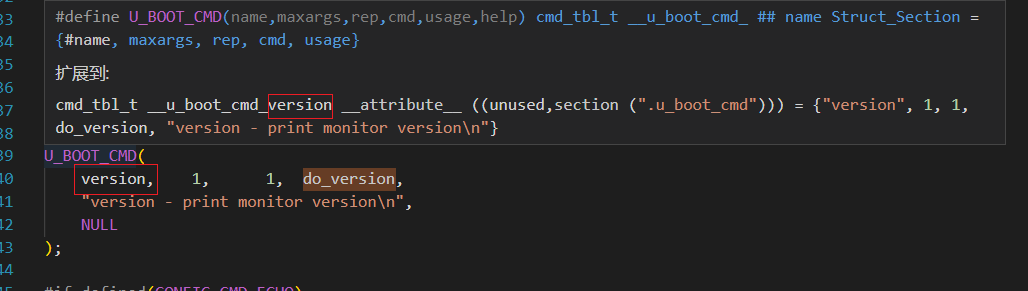
ARM uboot 源码分析7 - uboot的命令体系
一、uboot 命令体系基础 1、使用 uboot 命令 (1) uboot 启动后进入命令行环境下,在此输入命令按回车结束,uboot 会收取这个命令然后解析,然后执行。 2、uboot 命令体系实现代码在哪里 (1) uboot 命令体系的实现代码在 uboot/common/cmd_xx…...

物理服务器与云服务器备份相同吗?
自从云计算兴起以来,服务器备份已经从两阶段的模拟操作演变为由云服务器备份软件执行的复杂的多个过程。但是支持物理服务器和虚拟服务器之间的备份相同吗?主要区别是什么?我们接下来将详细讨论这个问题。 物理服务器与云服务器备份的区别 如果您不熟悉虚拟服务器…...

【Linux】system V共享内存 | 消息队列 | 信号量
🌠 作者:阿亮joy. 🎆专栏:《学会Linux》 🎇 座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根 目录👉system V共…...

FSC的宣传许可 答疑
【FSC的宣传许可 答疑】问:已经采购了认证产品但没有贴FSC标签,是否可以申请宣传许可?答:不可以。要宣传您采用了FSC认证产品的前提条件之一是产品必须是认证且贴有标签的。如果产品没有贴标,则不可申请宣传许可。您的…...

Leetcode力扣秋招刷题路-0100
从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结 100. 相同的树 给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是…...

协作对象死锁及其解决方案
协作对象死锁及其解决方案 1.前言 在遇到转账等的需要保证线程安全的情况时,我们通常会使用加锁的方式来保证线程安全,但如果无法合理的使用锁,很可能导致死锁。或者有时我们使用线程池来进行资源的使用,如调用数据库࿰…...

良许也成为砖家啦~
大家好,我是良许。 没错,良许成为砖家啦,绝不是口嗨,有图有真相! 有人会说,咦,这明明是严宇啊,跟你良许有啥关系? 额。。老读者应该知道良许的来历—— 鄙人真名严宇&a…...

Java中的编程细节
前言: 学习过程中有不少时候遇到一些看似简单,做起来事倍功半的问题。我也想自己是个聪明人,学东西一听就懂,一学就会,马上就能灵活应用。但这种事不能强求,要么自己要看个十遍二十遍最后理清逻辑…...
 环境搭建)
Yolov8从pytorch到caffe (一) 环境搭建
Yolov8从pytorch到caffe (一) 环境搭建 1. 创建虚拟环境2. 安装pytorch与v8相关库3. 测试安装是否成功4. 测试推理图像在windows上配置YOLOv8的环境,训练自己的数据集并转换到caffemodel1. 创建虚拟环境 利用conda创建虚拟环境 conda create -n yolo python=3.8 -y 并进入ac…...
)
2023年CDGA考试-第16章-数据管理组织与角色期望(含答案)
2023年CDGA考试-第16章-数据管理组织与角色期望(含答案) 单选题 1.在定义任何新组织或尝试改进现有组织之前了解当前组织的哪些方面非常重要? A.企业文化、运营模式和人员 B.业务战略、技术战略、数据战略 C.工具、方法和流程 D.事业环境因素、组织过程资产,行动路线图 …...

Stream——集合数据按照某一字段排序
文章目录前言假设业务场景排序前的准备正序排序1、数据集合的判空 Optional.isPresent()2、使用sort排序3、将排序后的数据流转换为list你以为这样就完了?倒序排序前言 之前,针对Stream链式编程中的几个方法做了大致的说明。详情可以参考: J…...

ubuntu:20.04编译arrow
1)拉取代码 git clone https://github.com/apache/arrow.git 2)切换分支 git checkout apache-arrow-11.0.0 3)拉入测试数据并设置环境变量 pushd arrow git submodule update --init export PARQUET_TEST_DATA"${PWD}/cpp/submodules/parquet-testing/da…...

2023如果纯做业务测试的话,在测试行业有出路吗?
直接抛出我的结论:手工做业务类测试,没有前途。 个人建议赶紧从业务测试跳出来,立即学习代码,走自动化测试方向。目前趋势,业务测试需要用自动化做。 为了让大家能够信服我的观点,本文将从以下方面进行阐…...

golang grpc ssl
无CA场景 在不考虑CA的场景下呢,client有client.key和client.crt,server有server.key和server.crt,生成方式可以如下: $ openssl genrsa -out server.key 2048 $ openssl req -new -x509 -days 3650 \-subj "/CGB/LChina/Og…...
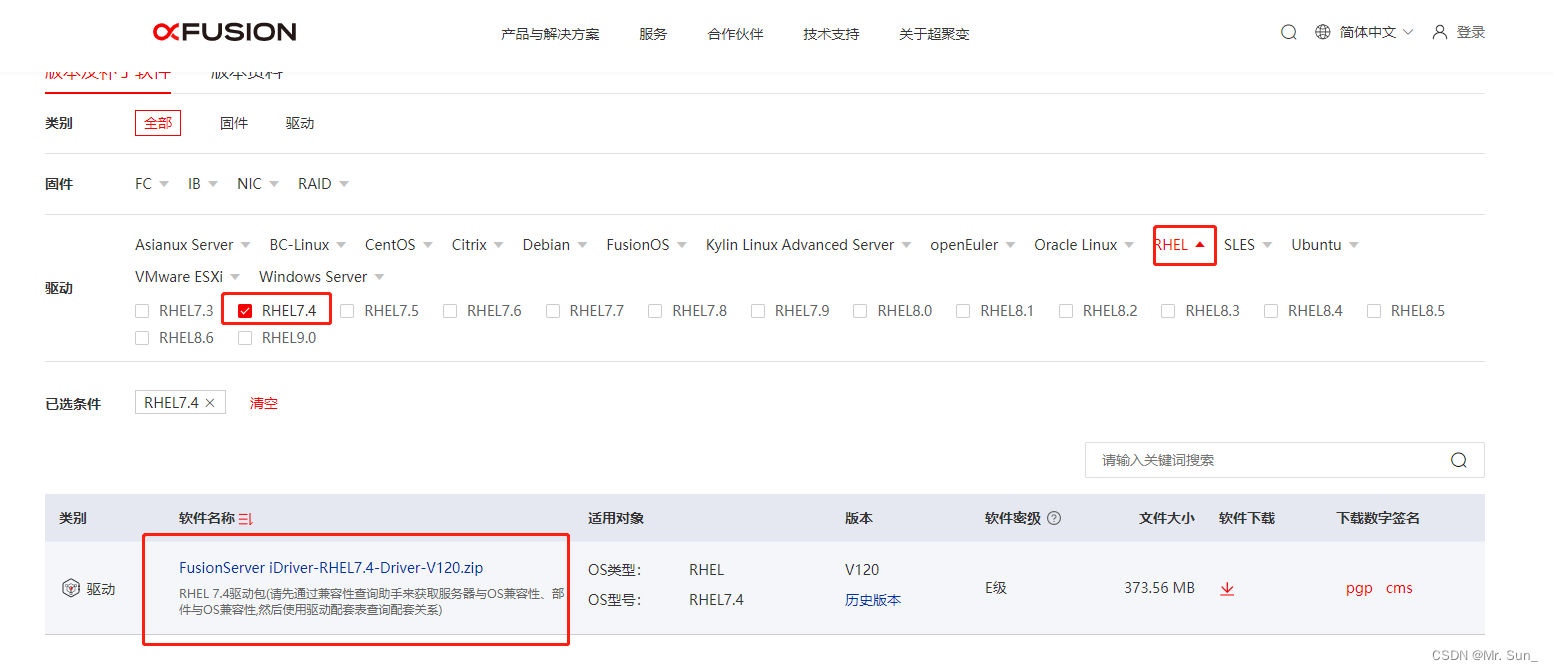
华为服务器驱动下载及安装
1.服务器技术支持网站 https://support.xfusion.com/support/#/zh/home 2.选择软件下载 3.选择服务器型号 4.选择驱动 5.根据需求选择驱动 例如红帽7.4系统 6.安装驱动 自动安装驱动步骤: 1)使用BMC虚拟光驱挂载onboard_driver_xxx.iso: 2)mount /dev/sr0 /mnt …...

【Shell】常用命令合集
常用命令: 文件和目录: cd /home 进入 ‘/home’ 目录 cd … 返回上一级目录 cd …/… 返回上两级目录 cd - 返回上次所在目录 cp file1 file2 将file1复制为file2 cp -a dir1 dir2 复制一个目录 cp -a /tmp/dir1 . 复制一个目录到当前工作目录(.代表当前目录…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
react更新页面数据,操作页面,双向数据绑定
// 路由不是组件的直接跳转use client,useEffect,useRouter,需3个结合, use client表示客户端 use client; import { Button,Card, Space,Tag,Table,message,Input } from antd; import { useEffect,useState } from react; impor…...
