【机器学习】sklearn降维算法PCA
文章目录
- 降维
- PCA
- sklearn中的PCA
- 代码实践
- PCA对手写数字数据集的降维
降维
如何实现降维?【即减少特征的数量,又保留大部分有效信息】
将那些带有重复信息的特征合并,并删除那些带无效信息的特征等等,逐渐创造出能够代表原特征矩阵大部分信息的,特征更少的,新特征矩阵。
在降维中,PCA使用的信息量衡量指标,就是样本方差,又称可解释性方差,方差越大,特征所带的信息量越多。
S 2 = 1 n − 1 ∑ i = 1 n ( x i − x ^ ) 2 S^2=\frac{1}{n-1}\sum_{i=1}^n(x_i-\hat{x})^2 S2=n−11i=1∑n(xi−x^)2
简单看一个二维降到一维的例子:
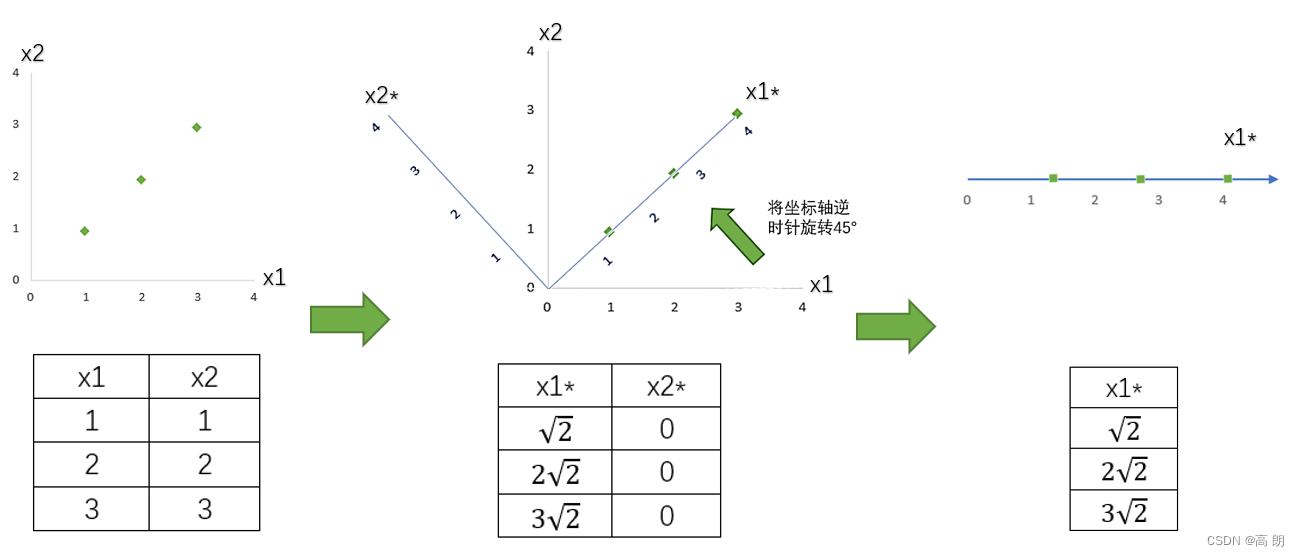 我们原本有两个特征
我们原本有两个特征x1和x2,同过将坐标系旋转45度形成一个新平面,形成两个新的特征和特征值,注意这时候 x 2 ∗ x2^* x2∗的方差是0,所以可以将 x 2 ∗ x2^* x2∗删除,同时也删除图中的 x 2 ∗ x2^* x2∗特征向量,剩下的 x 1 ∗ x1^* x1∗就代表了曾经需要两个特征来代表的三个样本点。
通过旋转原有特征向量组成的坐标轴来找到新特征向量和新坐标平面,我们将三个样本点的信息压缩到了一条直线上,实现了二维变一维,并且尽量保留原始数据的信息。一个成功的降维,就实现了。
以上面二维特征的降维推导到n维数据的降维:
| 过程 | 二维特征矩阵 | n维特征矩阵 |
|---|---|---|
| 1 | 输入原数据,结构为 (3,2) 找出原本的2个特征对应的直角坐标系,本质是找出这2个特征构成的2维平面 | 输入原数据,结构为 (m,n) 找出原本的n个特征向量构成的n维空间V |
| 2 | 决定降维后的特征数量:1 | 决定降维后的特征数量:k |
| 3 | 旋转,找出一个新坐标系 本质是找出2个新的特征向量,以及它们构成的新2维平面 新特征向量让数据能够被压缩到少数特征上,并且总信息量不损失太多 | 通过某种变化,找出n个新的特征向量,以及它们构成的新n维空间V |
| 4 | 找出数据点在新坐标系上,2个新坐标轴上的坐标 | 找出原始数据在新特征空间V中的n个新特征向量上对应的值,即“将数据映射到新空间中” |
| 5 | 选取第1个方差最大的特征向量,删掉没有被选中的特征,成功将2维平面降为1维 | 选取前k个信息量最大的特征,删掉没有被选中的特征,成功将n维空间V降为k维 |
在步骤3当中,我们用来找出n个新特征向量,让数据能够被压缩到少数特征上并且总信息量不损失太多的技术就是矩阵分解。
其中PCA和SVD都是采用矩阵分解的方式来对特征进行降维,两种算法中矩阵分解的方法不同,信息量的衡量指标不同。
PCA
PCA(Principal Component Analysis) 是一种常见的数据分析方式,常用于高维数据的降维,可用于提取数据的主要特征分量,所以常常也叫做主成分分析。
降维,降维的同时尽可能防止数据失真。
核心:构造新的坐标系,丢弃新的坐标系中的部分坐标,从而达到降维。
PCA过程:
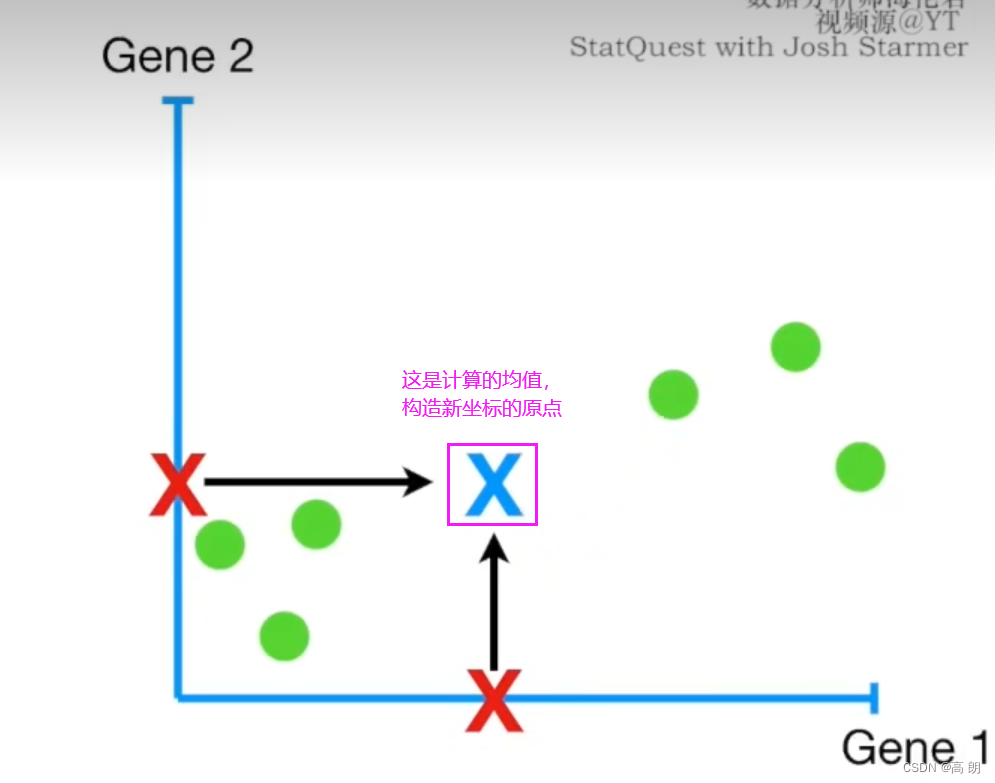
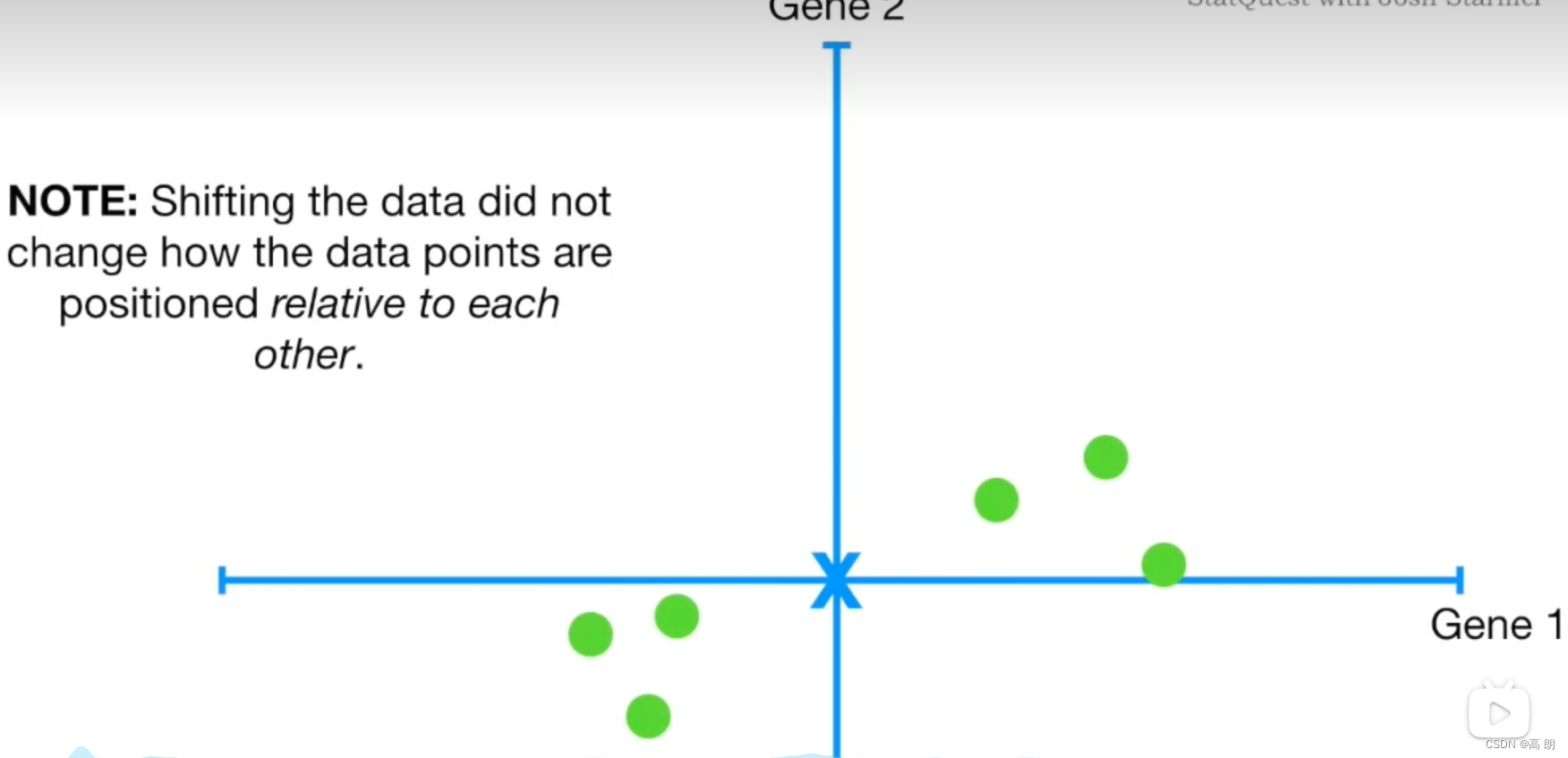
- 数据中心化。
求各样本点到坐标轴的平均值,然后对于所有的样例,都减去对应的均值。其目的是让数据通过中心化处理,得到均值为0的数据。同时中心化后的数据对向量来说也容易描述,因为是以原点为基准的。
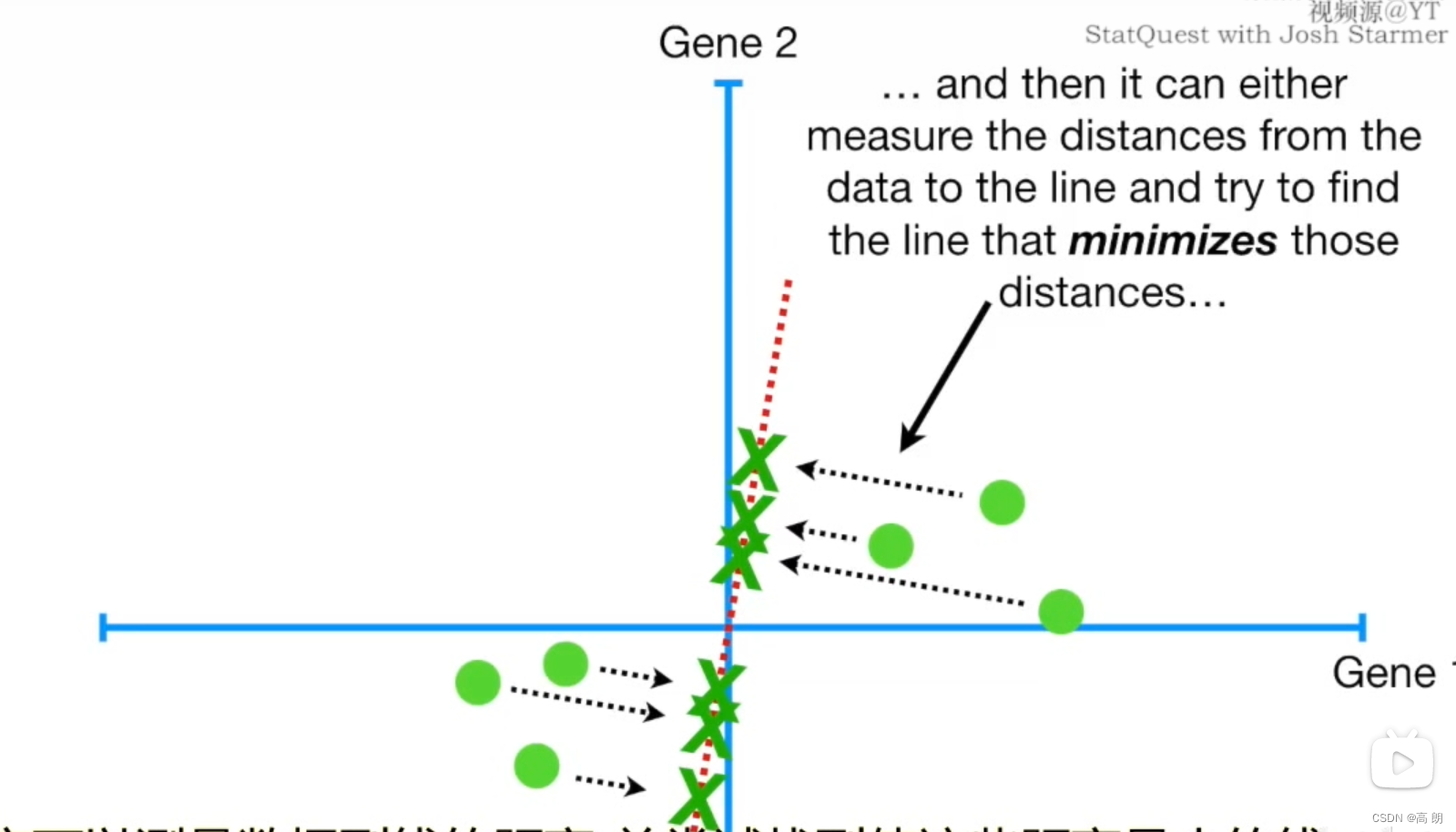
- 拟合线。
数据点到线的距离(越小越好)
数据点到线的距离越小,样本点到原点的距离不变【a的值是固定的】,要使b尽可能的小,根据勾股定理,就是使c尽可能的大,也就是各样本点投影到线上的投影点到原点的距离越大越好。
样本点到线的距离(越小越好)
各样本点投影到线上的投影点到原点的距离(越大越好)
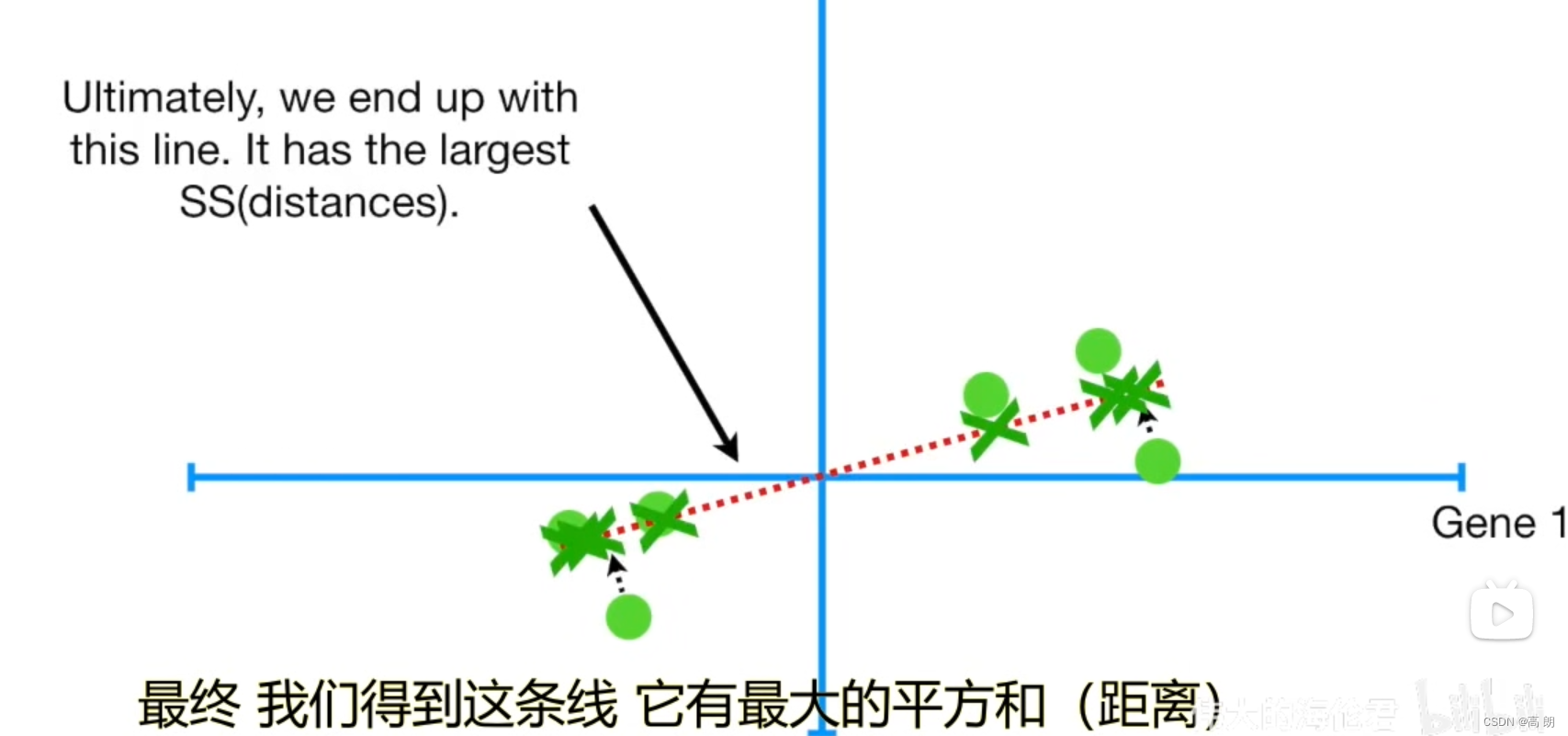
找到所有样本点投影到线上的投影点到原点的距离之和最大的线
这条线就是主成分1(PC1)
通过PC1,可以得出Gene1这个特征要比Gene2要重要,因为PC1中Gene1占的比重要大。
新的特征向量(拟合线):最佳拟合线也就是主成分线上的单位向量。
最佳拟合线的距离叫做PC1的特征值
根据其定义Ax=cx,其中A是矩阵,c是特征值,x是特征向量;
Ax矩阵相乘的含义就是,矩阵A对向量x进行一系列的变换(旋转或者拉伸),其效果等于一个常数c乘以向量x。
通常我们求特征值和特征向量是想知道,矩阵能使哪些向量(当然是特征向量)只发生拉伸,其拉伸程度如何(特征值的大小)。这个真正的意义在于,是为了让我们看清矩阵能在哪个方向(特征向量)产生最大的变化效果。
奇异值:
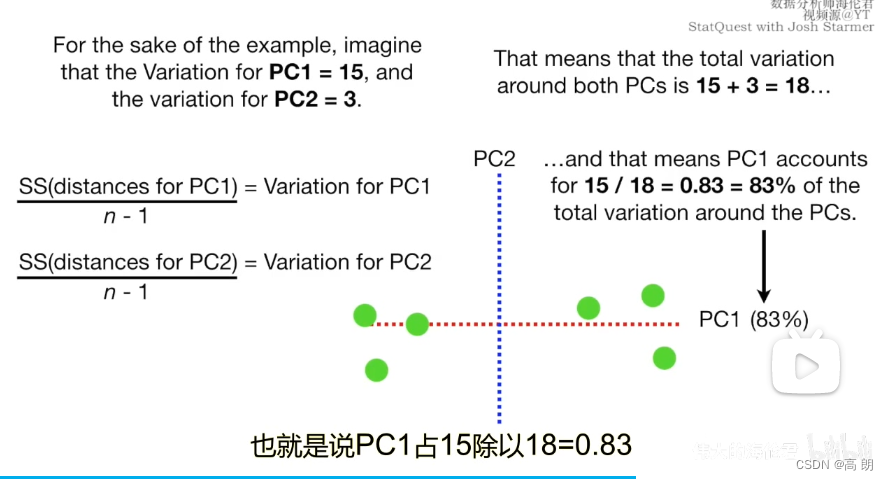 通过垂直PC1构造出PC2,分别计算各样本的到PC1和PC2的方差。然后各自方差除以方差之和得到差异率。
通过垂直PC1构造出PC2,分别计算各样本的到PC1和PC2的方差。然后各自方差除以方差之和得到差异率。
sklearn中的PCA
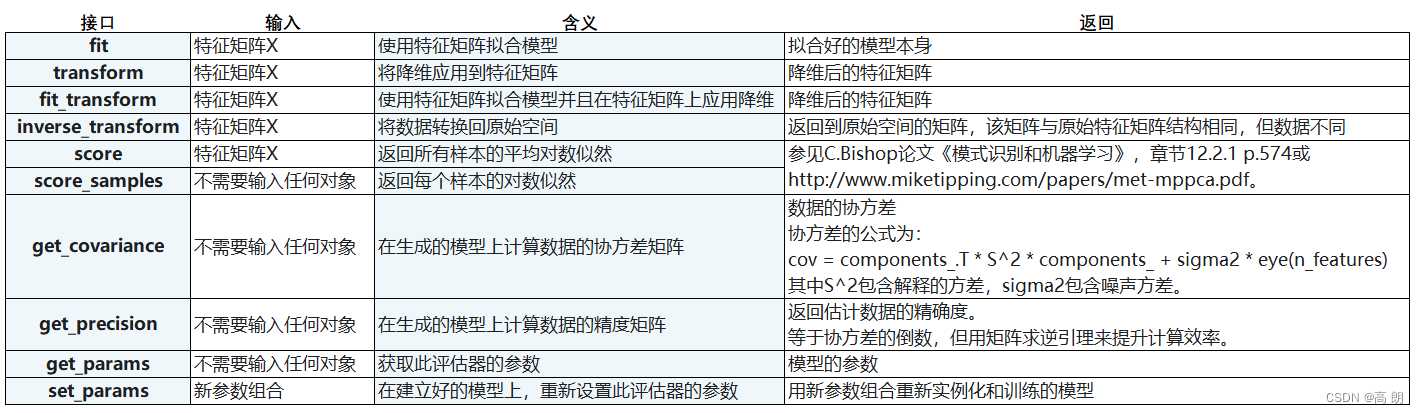
- 类:
sklearn.decomposition.PCA - 参数:



- 属性

- 接口
代码实践
- 导入库
import matplotlib.pyplot as plt # 画图工具
from sklearn.datasets import load_iris # 鸢尾花数据集
from sklearn.decomposition import PCA # PCA主成分分析类
- 查看原本数据集
iris = load_iris()
y = iris.target
X = iris.data
X.shape

可以看到鸢尾花数据集的特征是4维的。
- PCA进行降维
#调用PCA
pca = PCA(n_components=2) # 降到2维
pca = pca.fit(X) #拟合模型
X_dr = pca.transform(X) #获取新矩阵 (降维后的)
X_dr
#也可以fit_transform一步到位
#X_dr = PCA(2).fit_transform(X)

由原来的4维降到了2维,将降维后的特征通过2维平面画出来:
plt.figure()
plt.scatter(X_dr[y==0, 0], X_dr[y==0, 1], c="red", label=iris.target_names[0])
plt.scatter(X_dr[y==1, 0], X_dr[y==1, 1], c="black", label=iris.target_names[1])
plt.scatter(X_dr[y==2, 0], X_dr[y==2, 1], c="orange", label=iris.target_names[2])
plt.legend()
plt.title('PCA of IRIS dataset')
plt.show()
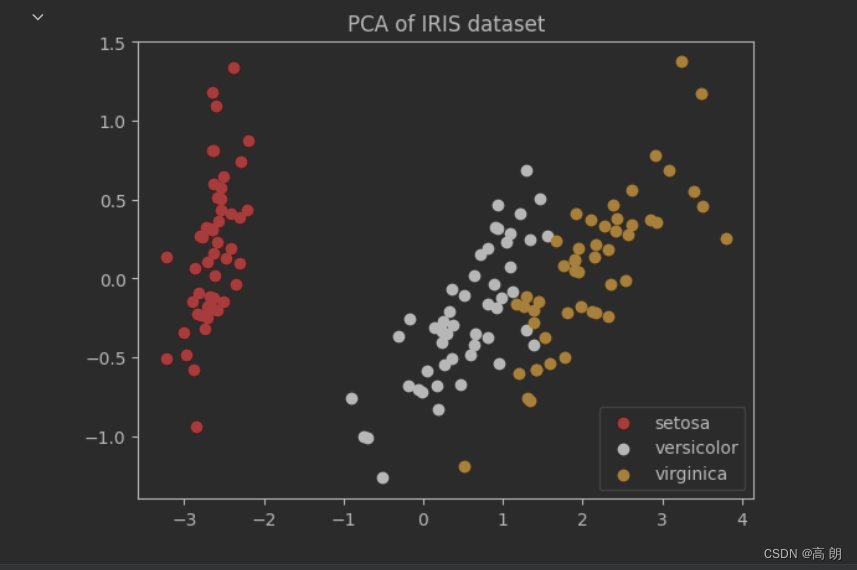 可以看到3种类型的数据是一簇一簇的,可以预料到KNN模型会有很好的表现。
可以看到3种类型的数据是一簇一簇的,可以预料到KNN模型会有很好的表现。
- 降维后数据探索
explained_variance_降维后每个新特征向量上所带的信息量大小explained_variance_ratio_上面那个的百分比
#属性explained_variance_,查看降维后每个新特征向量上所带的信息量大小(可解释性方差的大小)
pca.explained_variance_
#属性explained_variance_ratio,查看降维后每个新特征向量所占的信息量占原始数据总信息量的百分比
#又叫做可解释方差贡献率
pca.explained_variance_ratio_
#大部分信息都被有效地集中在了第一个特征上
pca.explained_variance_ratio_.sum()
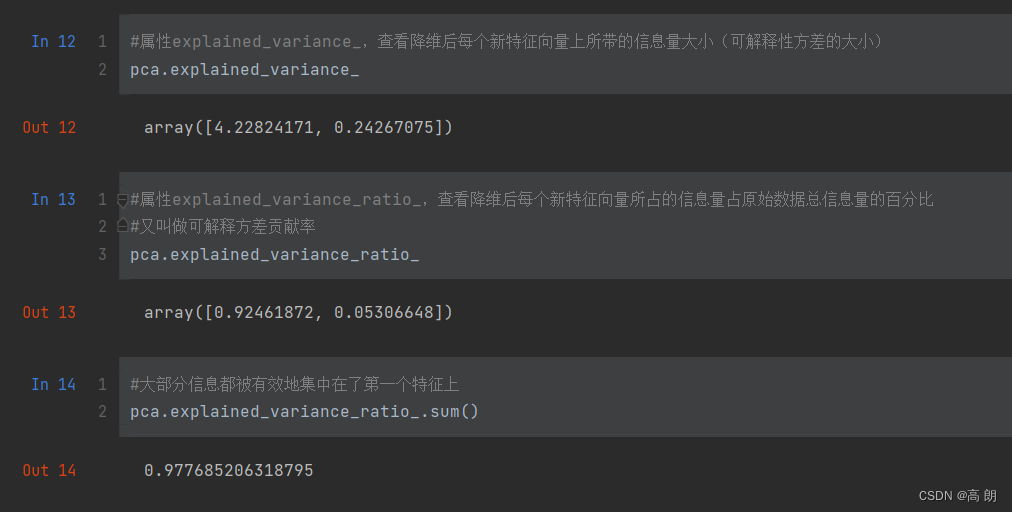
- 选择最好的n_components:累积可解释方差贡献率曲线
当参数n_components中不填写任何值,则默认返回min(X.shape)个特征,一般来说,样本量都会大于特征数目,所以什么都不填就相当于转换了新特征空间,但没有减少特征的个数。
可以通过查看转换了新特征空间后各个特征的占比。
import numpy as np
pca_line = PCA().fit(X)
plt.plot([1,2,3,4],np.cumsum(pca_line.explained_variance_ratio_))
plt.xticks([1,2,3,4]) #这是为了限制坐标轴显示为整数
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance ratio")
plt.show()
 一般选转折点,当
一般选转折点,当n_components=3时已经占比达到99%多了,基本可以选择这个。
- 最大似然估计自选超参数
n_components除了输入整数,还可以输入“mle”作为n_components的参数输入,了让PCA用最大似然估计(maximum likelihoodestimation)自选超参数的方法:
pca_mle = PCA(n_components="mle")
pca_mle = pca_mle.fit(X)
X_mle = pca_mle.transform(X)
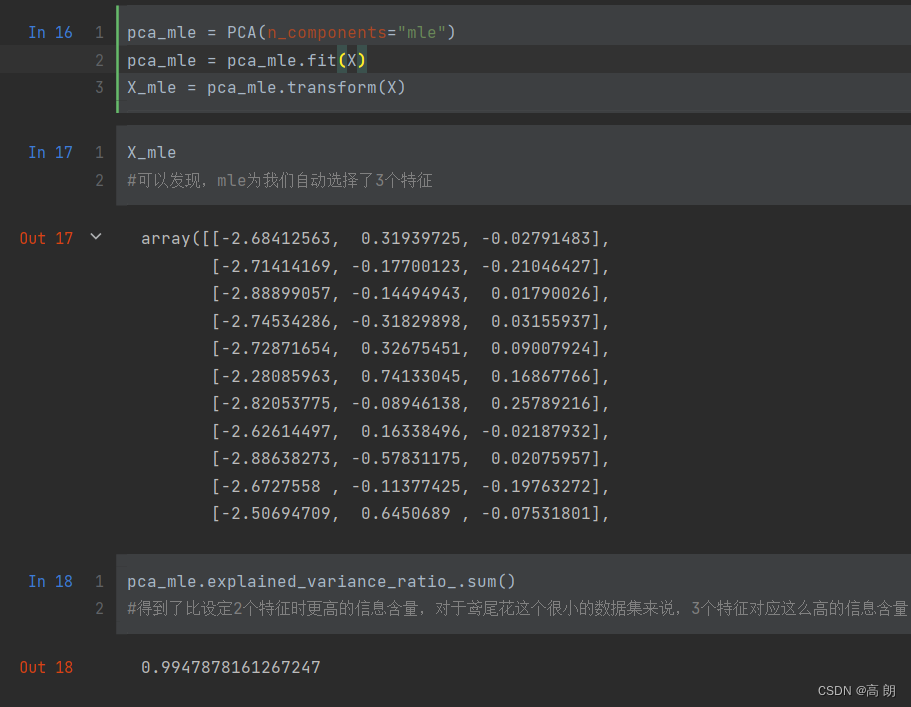 可以看得自动帮我们选择了降维到3.
可以看得自动帮我们选择了降维到3.
- 按信息量占比选超参数
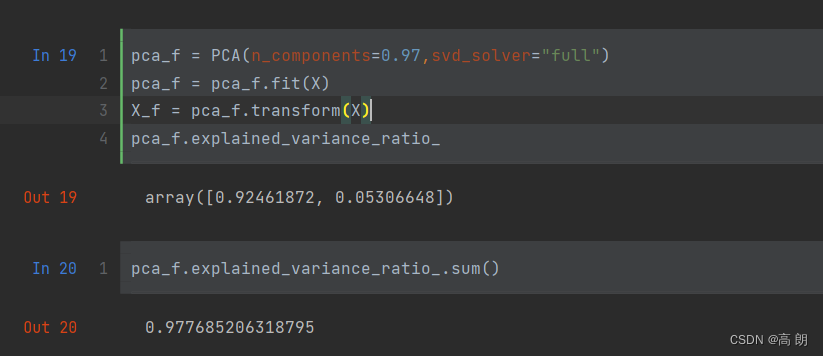
n_components还可以输入[0,1]的浮点数,搭配svd_solver="full"一起使用,表示希望降维后的总解释性方差占比大于n_components指定的百分比,即是说,希望保留百分之多少的信息量。
pca_f = PCA(n_components=0.97,svd_solver="full") # 降维后的数据占比大于97%
pca_f = pca_f.fit(X)
X_f = pca_f.transform(X)
- 原理
SVD可以找出一个新特征向量组成的n维空间, 而这个n维空间就是奇异值分解后的右矩阵 V T ( n , n ) V^T(n,n) VT(n,n),原特征需要降到k维
降维后的特征矩阵 X d r ( m , k ) = 原特征矩阵 X ( m , n ) ∗ V T [ : , k ] 降维后的特征矩阵X_{dr}(m,k)=原特征矩阵X(m,n)*V^T[:,k] 降维后的特征矩阵Xdr(m,k)=原特征矩阵X(m,n)∗VT[:,k]
k就是n_components,是我们降维后希望得到的维度。若X为(m,n)的特征矩阵, 就是结构为(n,n)的矩阵,取这个矩阵的前k行(进行切片),即将V转换为结构为(k,n)的矩阵。而 V ( k , n ) T V_{(k,n)}^T V(k,n)T与原特征矩阵X相乘,即可得到降维后的特征矩阵X_dr。这是说,奇异值分解可以不计算协方差矩阵等等结构复杂计算冗长的矩阵,就直接求出新特征空间和降维后的特征矩阵。
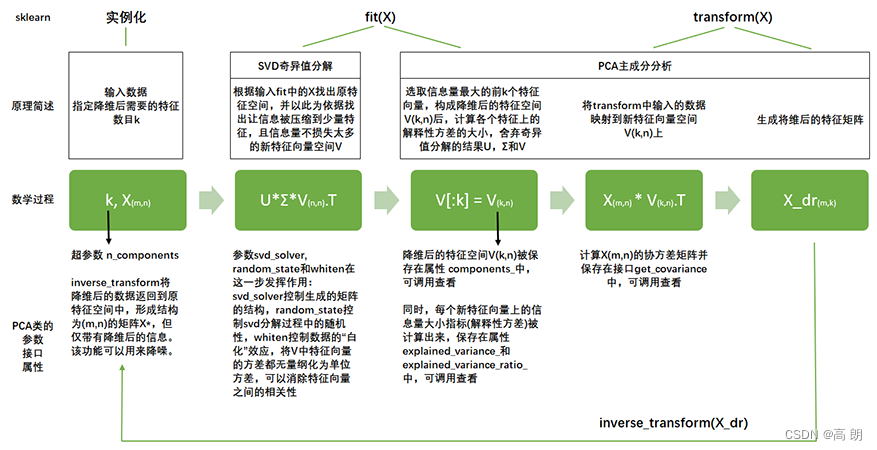
sklearn将降维流程拆成了两部分:一部分是计算特征空间V,由奇异值分解完成,另一部分是映射数据和求解新特征矩阵,由主成分分析完成,实现了用SVD的性质减少计算量,却让信息量的评估指标是方差,具体流程如下图:
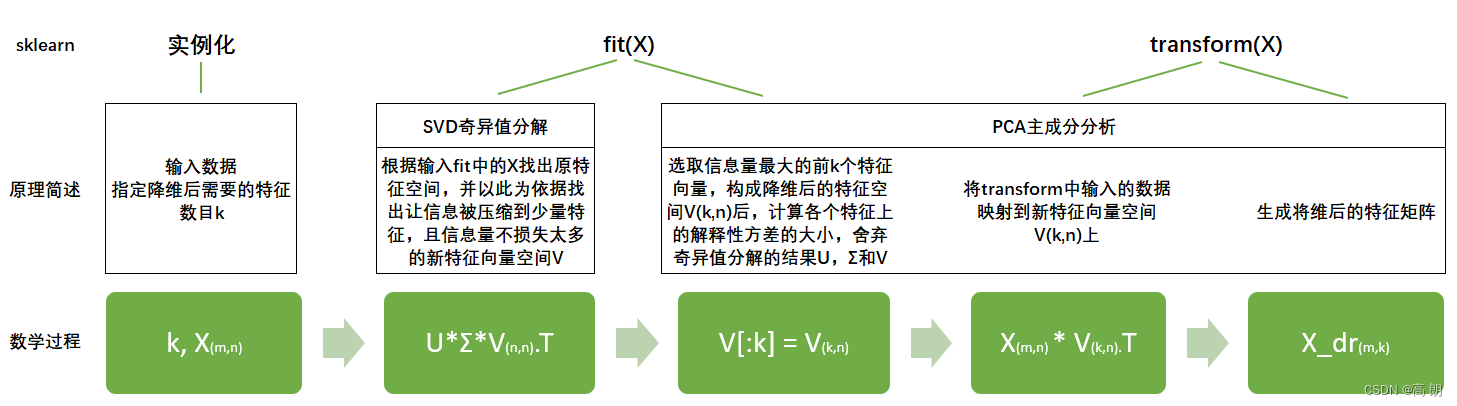
在sklearn中,矩阵U和Σ虽然会被计算出来(同样也是一种比起PCA来说简化非常多的数学过程,不产生协方差矩阵),但完全不会被用到,也无法调取查看或者使用,因此我们可以认为,U和Σ在fit过后就被遗弃了。奇异值分解追求的仅仅是V,只要有了V,就可以计算出降维后的特征矩阵。在transform过程之后,fit中奇异值分解的结果除了V(k,n)以外,就会被舍弃,而V(k,n)会被保存在属性components_ 当中,可以调用查看。
PCA(2).fit(X).components_ # (k,n) V矩阵
PCA(2).fit(X).components_.shape
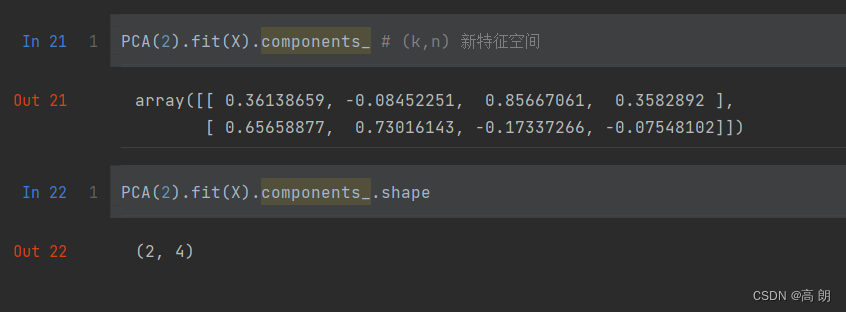
- 理解V(k,n),是新特征空间,是我们要将原始数据进行映射的那些新特征向量组成的矩阵。用它来
计算新的特征矩阵。
可以通过图像的降维来理解:
(1)导入库和数据集
from sklearn.datasets import fetch_lfw_people # 人脸数据
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
faces = fetch_lfw_people(data_home = "../pca/" ,download_if_missing=False, min_faces_per_person=60) #60是每个人最少提取60张
直接下载会报错forbidden403,直接自己下载
报错403 Forbidden 自己下载 https://pan.baidu.com/s/1J9lUvosuGJp6bLADzPN6aQ 提取码jqxx 解压后放入
(2)查看一下数据
 随便查看一下是什么样的图片:
随便查看一下是什么样的图片:
import matplotlib.pyplot as plt
fig, axes = plt.subplots(4,8,figsize=(8,4),subplot_kw={"xticks":[],"yticks":[]} # 不要显示坐标)
#填充图像
for i, ax in enumerate(axes.flat):ax.imshow(faces.images[i,:,:],cmap="gray" #选择色彩的模式)

(3)降维(降到150维)
X = faces.data
pca = PCA(150).fit(X)
V = pca.components_
查看要映射的矩阵V的信息
fig, axes = plt.subplots(3,8,figsize=(8,4),subplot_kw = {"xticks":[],"yticks":[]})
for i, ax in enumerate(axes.flat):ax.imshow(V[i,:].reshape(62,47),cmap="gray")
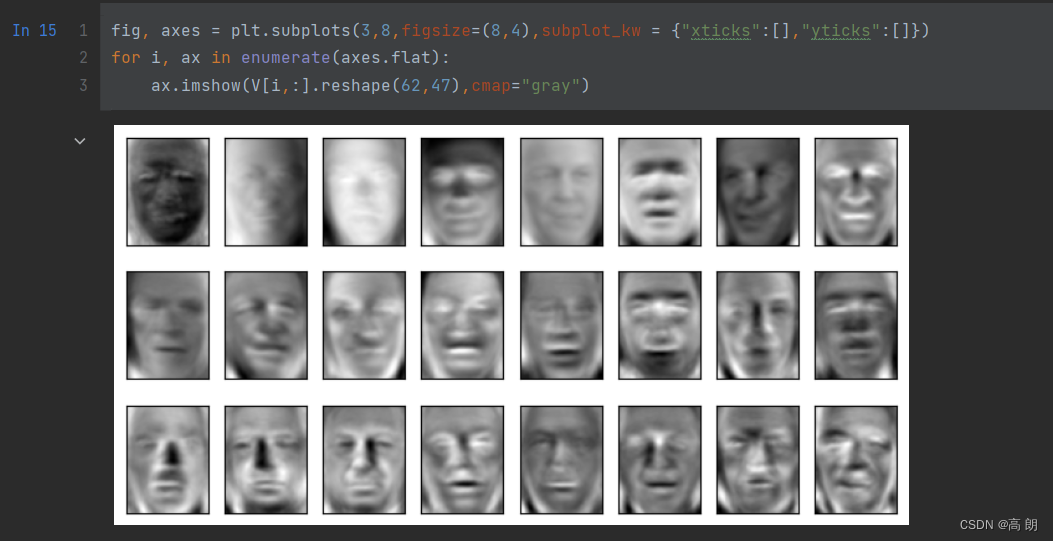
比起降维前的数据,新特征空间可视化后的人脸非常模糊,这是因为原始数据还没有被映射到特征空间中。但是可以看出,整体比较亮的图片,获取的信息较多,整体比较暗的图片,却只能看见黑漆漆的一块。
- 将降维后矩阵用inverse_transform返回原空间
X_inverse = pca.inverse_transform(X_dr)
fig, ax = plt.subplots(2,10,figsize=(10,2.5),subplot_kw={"xticks":[],"yticks":[]})
#现在我们的ax中是2行10列,第一行是原数据,第二行是inverse_transform后返回的数据
#所以我们需要同时循环两份数据,即一次循环画一列上的两张图,而不是把ax拉平
for i in range(10):ax[0,i].imshow(faces.images[i,:,:],cmap="binary_r")ax[1,i].imshow(X_inverse[i].reshape(62,47),cmap="binary_r")
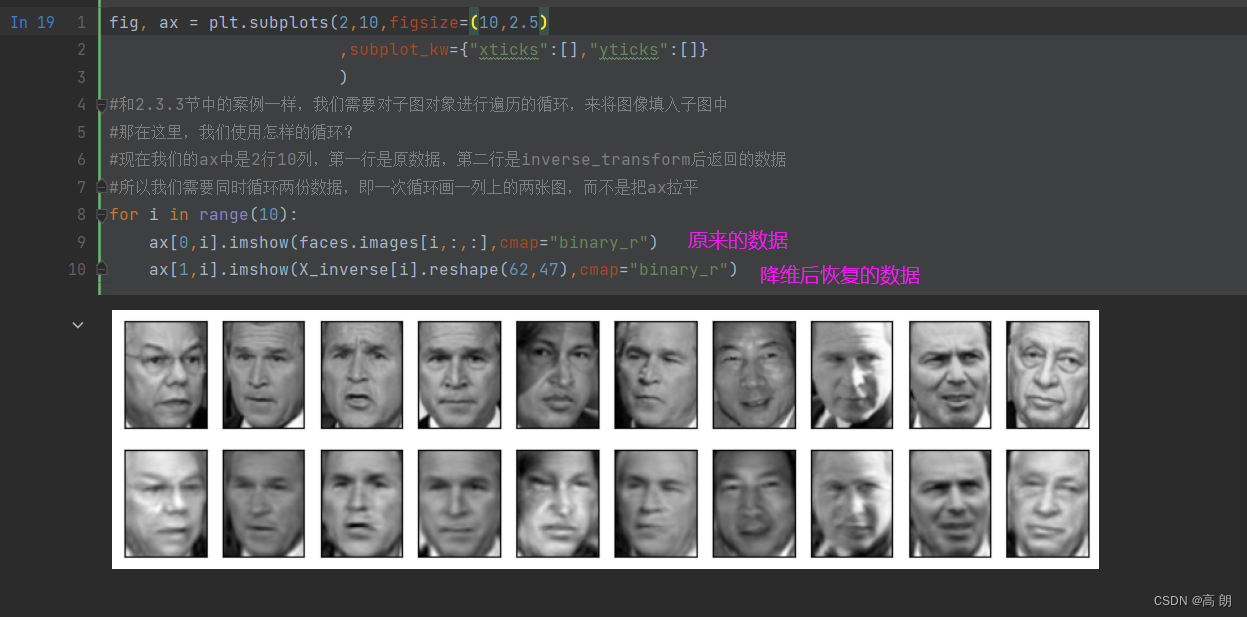 可以看得并不能完全复原,降维不是完全可逆的。
可以看得并不能完全复原,降维不是完全可逆的。
- 小结
PCA对手写数字数据集的降维
- 导入库
from sklearn.decomposition import PCA # pca降维
from sklearn.ensemble import RandomForestClassifier as RFC # 随机森林
from sklearn.model_selection import cross_val_score # 交叉验证
import matplotlib.pyplot as plt # 画图
import pandas as pd
import numpy as np
- 数据处理
data = pd.read_csv("./digit recognizor.csv")
X = data.iloc[:,1:]
y = data.iloc[:,0]
X.shape
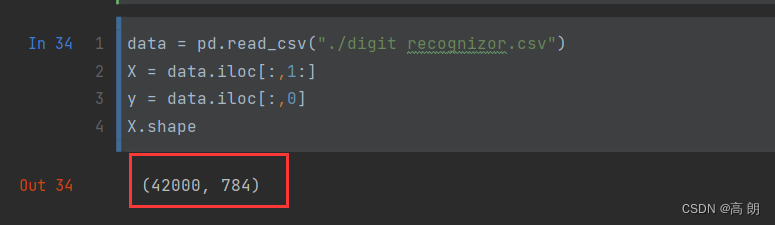 784维数据
784维数据
- 画累计方差贡献率曲线,找最佳降维后维度的范围
pca_line = PCA().fit(X)
plt.figure(figsize=[20,5])
plt.plot(np.cumsum(pca_line.explained_variance_ratio_))
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance ratio")
plt.show()
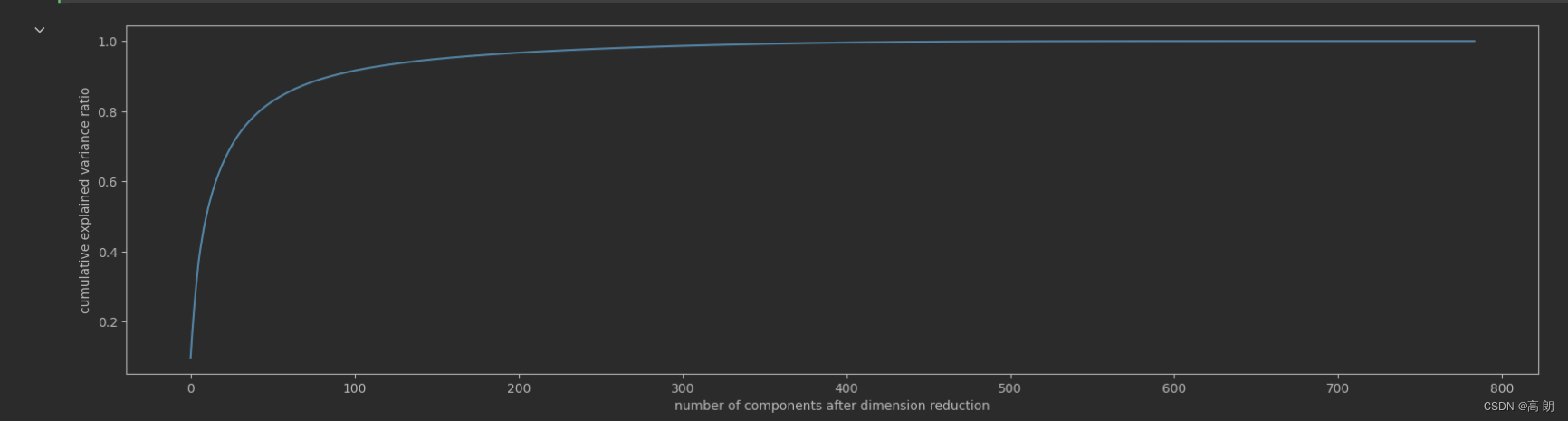 转折点在100前面,缩小范围,重新画学习曲线:
转折点在100前面,缩小范围,重新画学习曲线:
score = []
for i in range(1,101,10):X_dr = PCA(i).fit_transform(X)once = cross_val_score(RFC(n_estimators=10,random_state=0),X_dr,y,cv=5).mean()score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,101,10),score)
plt.show()
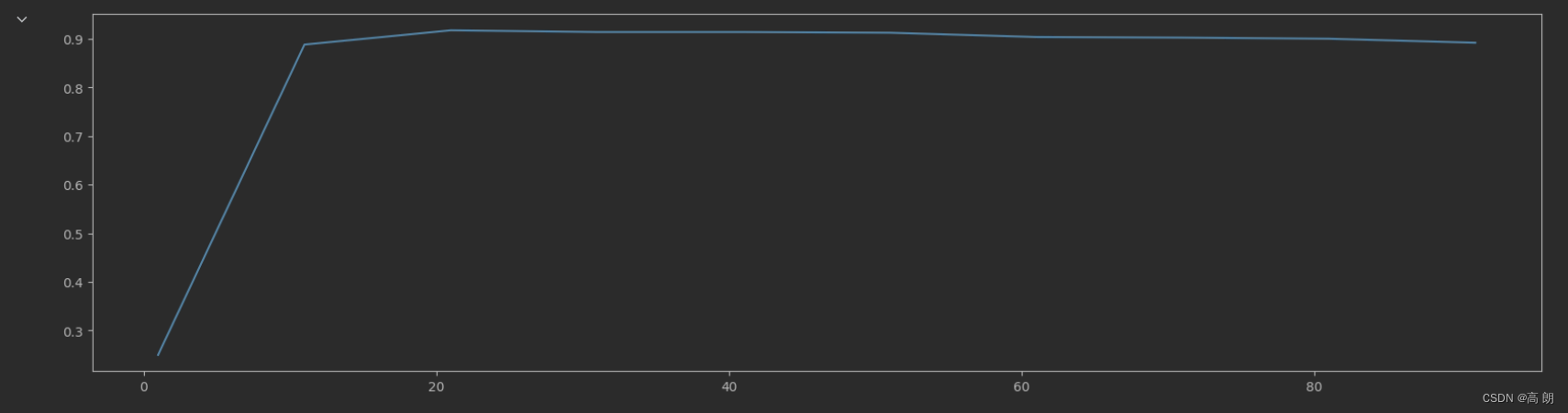 20很明显的一个转折点,再次缩小范围:
20很明显的一个转折点,再次缩小范围:
score = []
for i in range(10, 25):X_dr = PCA(i).fit_transform(X)once = cross_val_score(RFC(n_estimators=10,random_state=0),X_dr,y,cv=5).mean()score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10, 25),score)
plt.show()
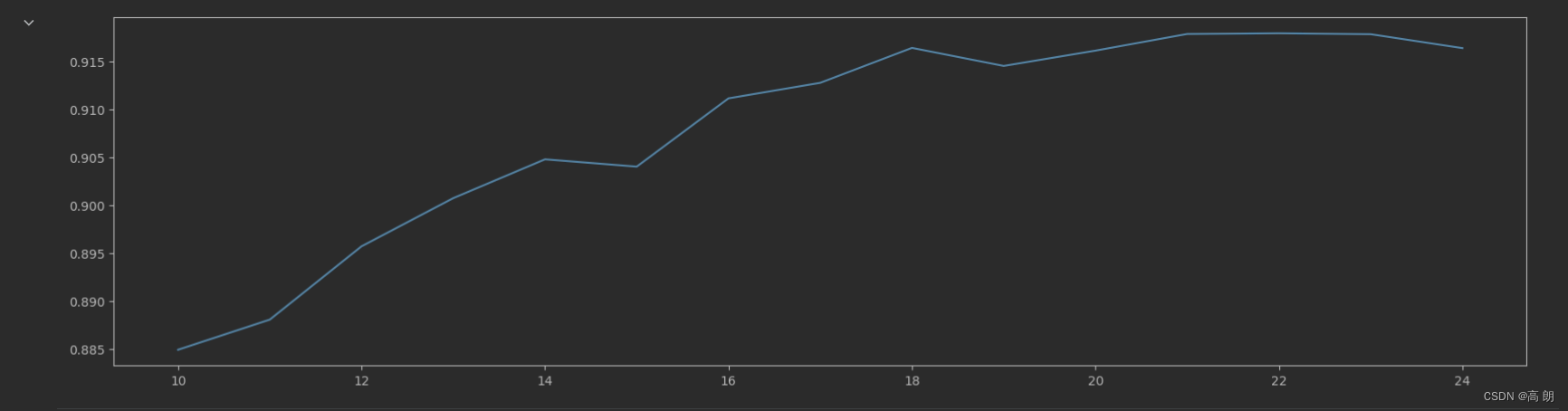 最佳点:21
最佳点:21
验证:
X_dr = PCA(21).fit_transform(X)
cross_val_score(RFC(n_estimators=10,random_state=0),X_dr,y,cv=5).mean()
可以再调一调n_estimators
cross_val_score(RFC(n_estimators=100,random_state=0),X_dr,y,cv=5).mean()
也可以试试其他模型:KNN
from sklearn.neighbors import KNeighborsClassifier as KNN
cross_val_score(KNN(),X_dr,y,cv=5).mean()
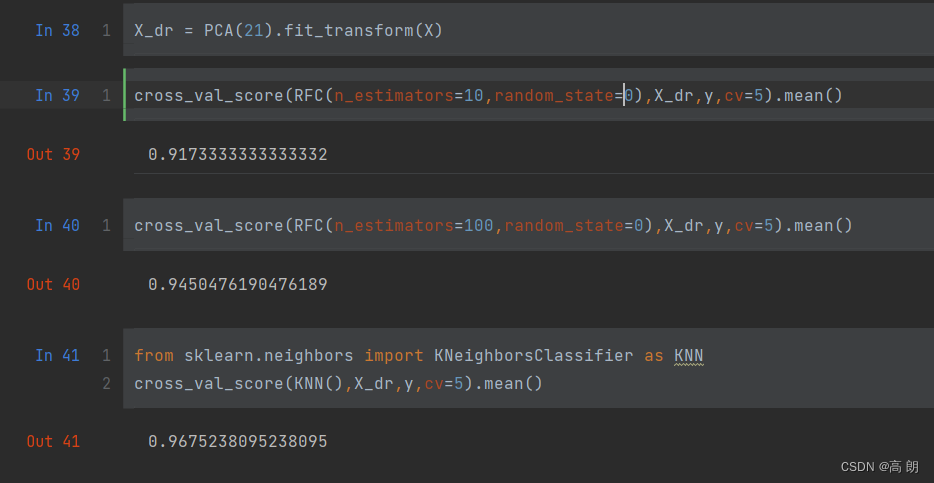 可以看到,由原来的七百多维降到21维后,准确率还能有90%多,效果非常不错,最高的达96%。
可以看到,由原来的七百多维降到21维后,准确率还能有90%多,效果非常不错,最高的达96%。
相关文章:

【机器学习】sklearn降维算法PCA
文章目录 降维PCAsklearn中的PCA代码实践 PCA对手写数字数据集的降维 降维 如何实现降维?【即减少特征的数量,又保留大部分有效信息】 将那些带有重复信息的特征合并,并删除那些带无效信息的特征等等,逐渐创造出能够代表原特征矩…...
华为云云耀云服务器L实例评测|企业项目最佳实践之评测用例(五)
华为云云耀云服务器L实例评测|企业项目最佳实践系列: 华为云云耀云服务器L实例评测|企业项目最佳实践之云服务器介绍(一) 华为云云耀云服务器L实例评测|企业项目最佳实践之华为云介绍(二) 华为云云耀云服务器L实例评测࿵…...
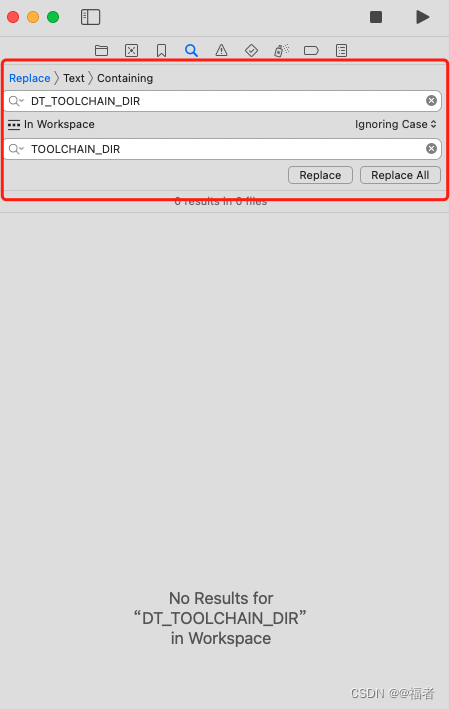
Xcode升级到15.0 解决DT_TOOLCHAIN_DIR问题
根据个人开发遇到的问题做的总结,公司要求Xcode 14.2 ,Swift 5.7开发,由于升级了Mac 14.0系统后,Xcode 14.2不能使用,解决方案目前有2个 一、在原来Xcode 14.2 的显示包内容,如图 二、升级到Xcode的15.0后…...
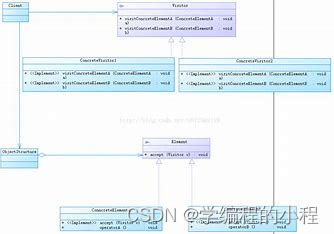
小谈设计模式(29)—访问者模式
小谈设计模式(29)—访问者模式 专栏介绍专栏地址专栏介绍 访问者模式角色分析访问者被访问者 优缺点分析优点将数据结构与算法分离增加新的操作很容易增加新的数据结构很困难4 缺点增加新的数据结构比较困难增加新的操作会导致访问者类的数量增加34 总结…...

【25】c++设计模式——>责任链模式
责任链模式定义 C中的责任链模式(Chain of Responsibility Pattern)是一种行为型设计模式,它通过将请求沿着处理对象的链传递来避免把请求发送者与接收者耦合在一起。 责任链模式的主要思想是,通过将多个处理对象组成一条链&…...

GlobalTransactional
seata-spring的maven坐标: <dependency><groupId>io.seata</groupId><artifactId>seata-spring</artifactId><version>1.6.1</version> </dependency>GlobalTransactional注解的位置: io.seata.sprin…...

Android Studio运行kotlin项目,一直Read timed out
Android Studio运行kotlin项目,一直Read timed out 下载别人的Kotlin项目,导入as后,运行app一直失败,提示Read timed out,有2种解决办法 第一种方式:gradle.properties 修改kotlin项目种的gradle.proper…...

Excel 的单元格内容和单元格格式
文章目录 单元格内容单元格格式常规格式数字格式 单元格内容 文本:只要不是纯数字,Excel 都默认是文本格式。 在 Excel 中,逻辑值只有两个:True 和 False。 全选一片区域,按 Delet 键删除内容时,确实可以删…...

4大软件测试策略的特点和区别(单元测试、集成测试、确认测试和系统测试)
四大软件测试策略分别是单元测试、集成测试、确认测试和系统测试。 一、单元测试 单元测试也称为模块测试,它针对软件中的最小单元(如函数、方法、类、模块等)进行测试,以验证其是否符合预期的行为和结果。单元测试通常由开发人…...

armbian 安装mysql
1、执行安装指令 sudo apt-get update sudo apt-get install mysql-server 2、安装成功后,设置密码 ALTER USER root% IDENTIFIED WITH mysql_native_password BY ysw1234; flush privileges;3、设置允许远程连接并生效 use mysql; update user set host % whe…...

Ubuntu22常用软件
别存太多重要东西在Ubuntu ,硬盘损坏就麻烦 Tweaks自定义UI sudo apt intall gnome-tweaks为了方便管理和添加,还需添加: sudo apt install gnome-shell-extension-prefs gnome-shell-extension-manager -y1.打开Extension应用,添…...
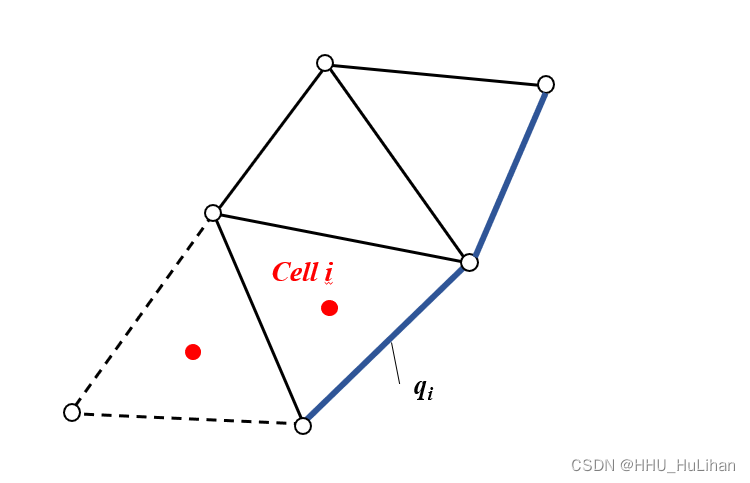
【CFD小工坊】浅水模型的边界条件
【CFD小工坊】浅水模型的边界条件 前言处理边界条件的原则边界处水力要素的计算水位边界条件单宽流量边界条件流量边界条件固壁边界条件 参考文献 前言 在浅水方程的离散及求解方法一篇中,我们学习了三角形网格各边通量值及源项的求解。但仍有一个问题没有解决&…...
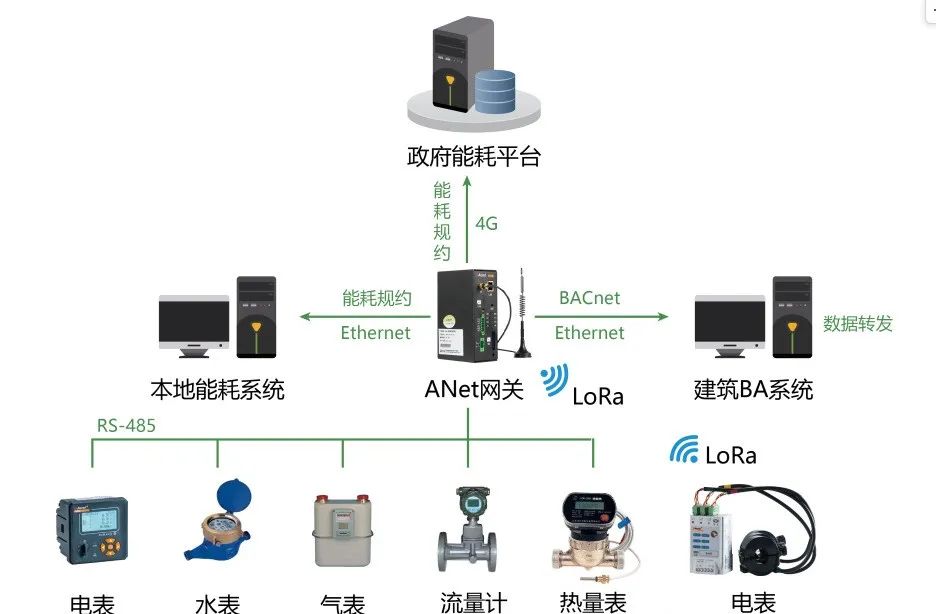
电力物联网关智能通讯管理机-安科瑞黄安南
众所周知,网关应用于各种行业的终端设备的数据采集与数据分析,然后去实现设备的监测、控制、计算,为系统与设备之间建立通讯联系,达到双向的数据通讯。 网关可以实时监测并及时发现异常数据,同时自身根据用户规则进行…...

用Flask构建一个AI翻译服务
缘起 首先,看一段代码,只有几行Python语句却完成了AI翻译的功能。 #!/usr/bin/python3import sys from transformers import MarianMTModel, MarianTokenizerdef translate(word_list):model_name "Helsinki-NLP/opus-mt-en-zh"tokenizer …...

微信小程序引入阿里巴巴iconfont图标并使用
介绍 在小程序里,使用阿里巴巴的图标,如下所示: 使用方式 搜索自己需要的图标,然后将需要用到的图标加入购物车,如下图所示: 去右上角,点击购物车按钮;这里第一次使用,会有三个提…...

mysql面试题49:MySQL中不同text数据类型的最大长度
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:MySQL中TEXT数据类型的最大长度 在MySQL中,TEXT数据类型用于存储较大…...

从虚拟电厂在上海的实践探索看企业微电网数字化的意义
安科瑞 华楠 作为典型的人口聚集、负荷密集区域,上海市具有外来电比例高、本地资源禀赋不足的特点。从发电侧角度来看,近年来上海风、光等新能源发电装机比例逐年提升,传统的火电逐渐成为调节性发电资源;从负荷侧角度来看上海以第…...

创建并初始化线程池
创建并初始化线程池–》threadpool.h, 创建并初始化&脱离(执行完后)子线程,每个子线程信号量wait阻塞【1】 创建套接字:int listenfd socket( PF_INET, SOCK_STREAM, 0 ); 端口复用:setsockopt( listenfd, SOL_SOCKET, SO_REUSEADDR, &a…...
【LeetCode热题100】--136.只出现一次的数字
136.只出现一次的数字 使用哈希表: class Solution {public int singleNumber(int[] nums) {Map<Integer,Integer> map new HashMap<>();for(int num:nums){Integer count map.get(num);if(count null){count 1;}else{count;}map.put(num,count);}…...
Java idea查看自定义注解的调用地方
Java idea查看自定义注解的调用地方...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...