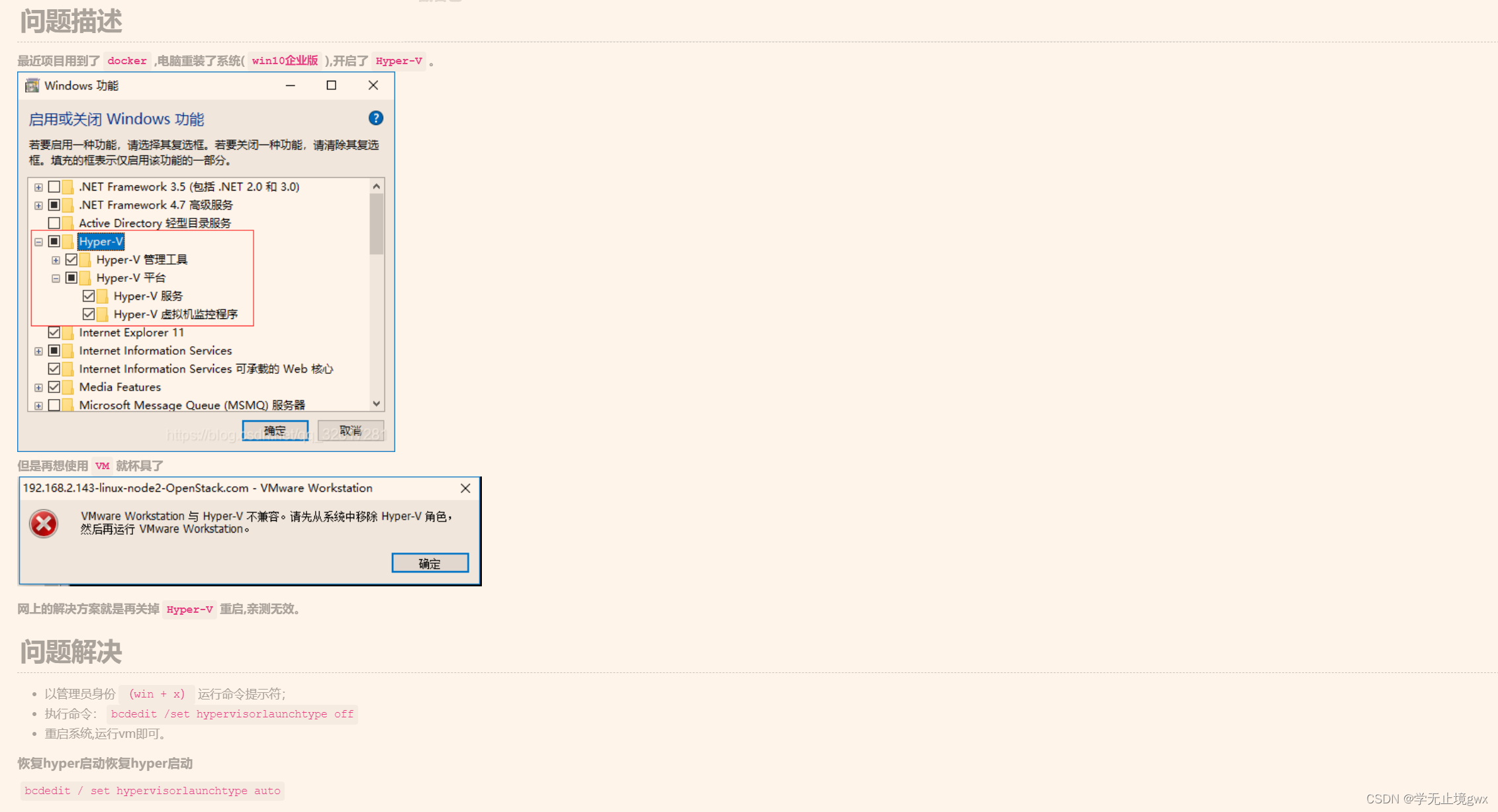
数据结构 优先级队列(堆)
数据结构 优先级队列(堆)
文章目录
- 数据结构 优先级队列(堆)
- 1. 优先级队列
- 1.1 概念
- 2. 优先级队列的模拟实现
- 2.1 堆的概念
- 2.2 堆的存储方式
- 2.3 堆的创建
- 2.3.1 堆向下调整
- 2.3.2 堆的创建
- 2.3.3 建堆的时间复杂度
- 2.4 堆的插入与删除
- 2.4.1 堆的插入
- 2.4.2 堆的删除
- 2.5 用堆模拟实现优先级队列
- 3. 常用接口介绍
- 3.1 PriorityQueue的特性
- 3.2 PriorityQueue常用接口介绍
- **3.2.1 优先级队列的构造**
- 3.2.2 插入/删除/获取优先级最高的元素
- 3.3 OJ练习
- 4. 堆的应用
1. 优先级队列
1.1 概念
在前面的文章里曾介绍过队列,队列是一种先进先出的数据结构,但有些情况下,我们需要操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列
在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)
2. 优先级队列的模拟实现
JDK1.8中的PriorityQueue底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整
2.1 堆的概念
如果有一个关键码的集合K = {k0, k1, k2, … , kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:ki<=k2i+1且ki <= k2i+2(ki>=k2i+1 且ki>=k2i+2) i = 0, 1, 2…, 则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
大根堆:根节点大于左右节点
小根堆:根节点小于左右节点
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树

2.2 堆的存储方式
从堆的概念可知,堆是一棵完全二叉树,因此可以采用顺序存储的方式来进行高效存储

注:对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低
将元素存储到数组中后,可以根据我们在二叉树文章中介绍到的性质5堆树进行还原。假设i为节点在数组中的下标,则有:
- 如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为
(i-1)/2 - 如果2 * i + 1 小于节点个数,则节点i的左孩子下标为
2 * i + 1,否则没有左孩子 - 如果2 * i + 2 小于节点个数,则节点i的右孩子下标为
2 * i + 2,否则没有右孩子
2.3 堆的创建
2.3.1 堆向下调整
对于集合{27, 15, 19, 18, 28, 34, 65, 49, 25, 37} 中的数据,如果想要将它创建成堆又该怎么操作?

仔细观察上图后发现:根节点的左右子树已经完全满足堆的性质,因此在这里只需要将根节点向下调整好即可
向下调整(这里我们以小根堆为例):
- 使用
parent标记需要标记的根节点,child标记parent的左孩子(parent如果有孩子一定是先有左孩子) - 如果parent的左孩子存在,即:child < size,进行以下操作,直到parent的左孩子不存在:
- 判断parent右孩子是否存在,存在找到左右孩子中最小的孩子,让child进行标记
- 将parent与较小的孩子child进行比较,如果:
- parent小于较小的孩子child,调整结束
- 否则:交换parent与较小的孩子child,交换完成之后,继续向下调整,即parent = child;child = parent * 2 + 1

代码示例:
public void shiftSmallDown(int parent,int len) {//左孩子int child = 2 * parent + 1;while(child < len) {//判断是否存在右孩子 且右孩子和左孩子哪个更小,小的为childif (child+1 < len && elem[child+1] < elem[child]) {child++;}//判断根节点和child的大小,若根节点小则结束遍历,否则交换两个节点if (elem[child] < elem[parent]) {swap(child, parent);parent = child;child = 2 * parent + 1;}else {break;}}}public void createSmallHeap() {for (int parent = (usderSize-1-1)/2;parent >= 0;parent--) {shiftSmallDown(parent, usderSize);}}public void swap(int x, int y) {int temp = elem[x];elem[x] = elem[y];elem[y] = temp;}

2.3.2 堆的创建
上述举的例子为特殊情况(即左右子树已经满足堆的特性,只需要修改根节点),那对于普通的序列{1, 5, 3, 8, 7, 6},即根节点的左右子树不满足堆的特性时,又该如何调整?(这里我们以大根堆为例)

在这里,我们找倒数第一个非叶子节点,从该节点位置开始往前一直到根节点,每遇到一个节点,应用向下调整
代码示例:
public void shiftBigDown(int parent,int len) {//左孩子int child = 2 * parent + 1;while(child < len) {//判断是否存在右孩子 且右孩子和左孩子哪个更大,大的为childif (child+1 < len && elem[child+1] > elem[child]) {child++;}//判断根节点和child的大小,若根节点大则结束遍历,否则交换两个节点if (elem[child] > elem[parent]) {swap(child, parent);parent = child;child = 2 * parent + 1;}else {break;}}}
public void swap(int x, int y) {int temp = elem[x];elem[x] = elem[y];elem[y] = temp;}
public void createBigHeap() {//找倒数第一个非叶子节点,从该节点位置开始往前一直到根节点,每遇到一个节点,应用向下调整for (int parent = (usderSize-1-1)/2;parent >= 0;parent--) {shiftBigDown(parent, usderSize);}}

2.3.3 建堆的时间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果):

因此,建堆的时间复杂度为O(N)
2.4 堆的插入与删除
2.4.1 堆的插入
堆的插入总共需要两个步骤:
- 先将元素放到底层空间中(注:空间不够时需要扩容)
- 将最后新插入的节点向上调整,直到满足堆的性质

代码示例:
public void push(int val) {// 满了则扩容if (isFull()) {elem = Arrays.copyOf(elem,2*elem.length);}elem[usderSize] = val;//向上调整shiftBigUp(usderSize);usderSize++;}private boolean isFull() {return usderSize == elem.length;}/*** 向上调整* 这里以大根堆为例*/public void shiftBigUp(int child) {int parent = (child - 1)/2;while(child > 0) {if (elem[parent] < elem[child]) {swap(child,parent);child = parent;parent = (child - 1) / 2;}else {break;}}}public void swap(int x, int y) {int temp = elem[x];elem[x] = elem[y];elem[y] = temp;}

2.4.2 堆的删除
堆删除的一定是堆顶元素,操作方法如下:
- 将堆顶元素与堆中最后一个元素交换
- 将堆中有效数据个数减少一个
- 对堆顶元素进行向下调整

代码示例:
/*删除元素*/
public int pop() {if (empty()) {return -1;}int oldVal = elem[0];swap(0,usderSize-1);usderSize--;shiftBigDown(0,usderSize);return oldVal;}
public boolean empty() {return usderSize == 0;}public void shiftBigDown(int parent,int len) {//左孩子int child = 2 * parent + 1;while(child < len) {//判断是否存在右孩子 且右孩子和左孩子哪个更大,大的为childif (child+1 < len && elem[child+1] > elem[child]) {child++;}//判断根节点和child的大小,若根节点大则结束遍历,否则交换两个节点if (elem[child] > elem[parent]) {swap(child, parent);parent = child;child = 2 * parent + 1;}else {break;}}}

2.5 用堆模拟实现优先级队列
代码示例:
package demo2;public class MyPriorityQueue {public int[] arr = new int[100];public int size = 0;public void offer(int e) {arr[size] = e;shiftBigUp(size);size++;}public int poll() {int oldval = arr[0];swap(0,size-1);size--;shiftBigDown(0,size);return oldval;}public int peek() {return arr[0];}public void shiftBigUp(int child) {int parent = (child - 1)/2;while(child > 0) {if (arr[parent] < arr[child]) {swap(child,parent);child = parent;parent = (child - 1) / 2;}else {break;}}}public void shiftBigDown(int parent,int len) {//左孩子int child = 2 * parent + 1;while(child < len) {//判断是否存在右孩子 且右孩子和左孩子哪个更大,大的为childif (child+1 < len && arr[child+1] > arr[child]) {child++;}//判断根节点和child的大小,若根节点大则结束遍历,否则交换两个节点if (arr[child] > arr[parent]) {swap(child, parent);parent = child;child = 2 * parent + 1;}else {break;}}}public void swap(int x, int y) {int temp = arr[x];arr[x] = arr[y];arr[y] = temp;}public void display() {for (int i = 0;i < size;i++) {System.out.print(arr[i] + " ");}}
}

3. 常用接口介绍
3.1 PriorityQueue的特性
Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,本文主要介绍PriorityQueue

使用PriorityQueue时需要注意:
-
使用时必须导入PriorityQueue所在的包,即:
import java.util.PriorityQueue; -
PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出
ClassCastException异常 -
不能插入null对象,否则会抛出
NullPointeException -
没有容量限制,可以插入任意多个元素,其内部可以自动扩容
-
插入和删除元素的时间复杂度为O(log₂N)
-
PriorityQueue底层使用了堆数据结构
-
PriorityQueue默认情况下是小根堆–即每次获取到的元素都是最小的元素
3.2 PriorityQueue常用接口介绍
3.2.1 优先级队列的构造
| 构造器 | 功能介绍 |
|---|---|
| PriorityQueue() | 创建一个空的优先级队列,默认容量是11 |
| PriorityQueue(int initialCapacity) | 创建一个初始容量为initialCapacity的优先级队列,注意: initialCapacity不能小于1,否则会抛IllegalArgumentException异 常 |
| PriorityQueue(Collection<? extends E> c) | 用一个集合来创建优先级队列 |
package demo3;import java.util.ArrayList;
import java.util.PriorityQueue;public class TestPriorityQueue {public static void main(String[] args) {// 创建一个空的优先级队列,底层默认容量是11PriorityQueue<Integer> q1 = new PriorityQueue<>();// 创建一个空的优先级队列,底层默认容量是initialCapacityPriorityQueue<Integer> q2 = new PriorityQueue<>(100);ArrayList<Integer> list = new ArrayList<>();list.add(1234);list.add(123);list.add(12);list.add(1);// 用ArrayList对象来构造一个优先级队列的对象//此时q3中已经包含了三个元素PriorityQueue<Integer> q3 = new PriorityQueue<>(list);System.out.println(q3);System.out.println("size = " + q3.size());System.out.println("队头元素为:" + q3.peek());}}

注:默认情况下,PriorityQueue队列是小根堆,如果需要大根堆需要用户提供比较器
class IntCmp implements Comparator<Integer> {public int compare(Integer o1, Integer o2) {return o2 - o1;}
}//大根堆构建优先级队列PriorityQueue<Integer> q4 = new PriorityQueue<>(new IntCmp());q4.offer(4);q4.offer(3);q4.offer(2);q4.offer(1);q4.offer(5);System.out.println(q4);

此时创建出来的就是一个大根堆
3.2.2 插入/删除/获取优先级最高的元素
| 函数名 | 功能介绍 |
|---|---|
| boolean offer(E e) | 插入元素e,插入成功返回true,如果e对象为空,抛出NullPointerException异常,时 间复杂度 ,注意:空间不够时候会进行自动扩容 |
| E peek() | 获取优先级最高的元素,如果优先级队列为空,返回null |
| E poll() | 移除优先级最高的元素并返回,如果优先级队列为空,返回null |
| int size() | 获取有效元素的个数 |
| void clear() | 清空 |
| boolean isEmpty() | 检测优先级队列是否为空,空返回true |
package demo3;import java.util.PriorityQueue;public class TestPriorityQueue2 {public static void main(String[] args) {int[] arr = {4, 1, 9, 2, 8, 0, 7, 3, 6, 5};//如果知道元素个数建议直接给底层容量PriorityQueue<Integer> q = new PriorityQueue<>(arr.length); // 注:默认时为小根堆//插入元素for (int e:arr) {q.offer(e);}System.out.println(q);System.out.println(q.peek()); // 获取优先级最高的元素System.out.println(q.size()); // 打印优先级队列中有效元素的个数//弹出元素q.poll();System.out.println(q);q.offer(0); // 插入元素后优先级会发生改变System.out.println(q);//清空队列q.clear();if (q.isEmpty()) {System.out.println("优先级队列为空");}else {System.out.println("优先级队列不为空");}}
}

3.3 OJ练习
top-k问题:求最大或者最小的前k个数据
代码示例:
import java.util.PriorityQueue;
class Solution {public int[] smallestK(int[] arr, int k) {int[] ret = new int[k];if (k == 0 || arr == null) {return ret;}PriorityQueue<Integer> q = new PriorityQueue<>(arr.length);for (int e:arr) {q.offer(e);}for (int i = 0;i < k;i++) {ret[i] = q.poll();}return ret;}
}

4. 堆的应用
这里我们拓展一下堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
-
建堆:
- 升序:建大堆
- 降序:建小堆
-
利用堆删除思想来进行排序:
建堆和堆删除中都用到了向下调整,因此掌握向下调整,就可以完成堆排序

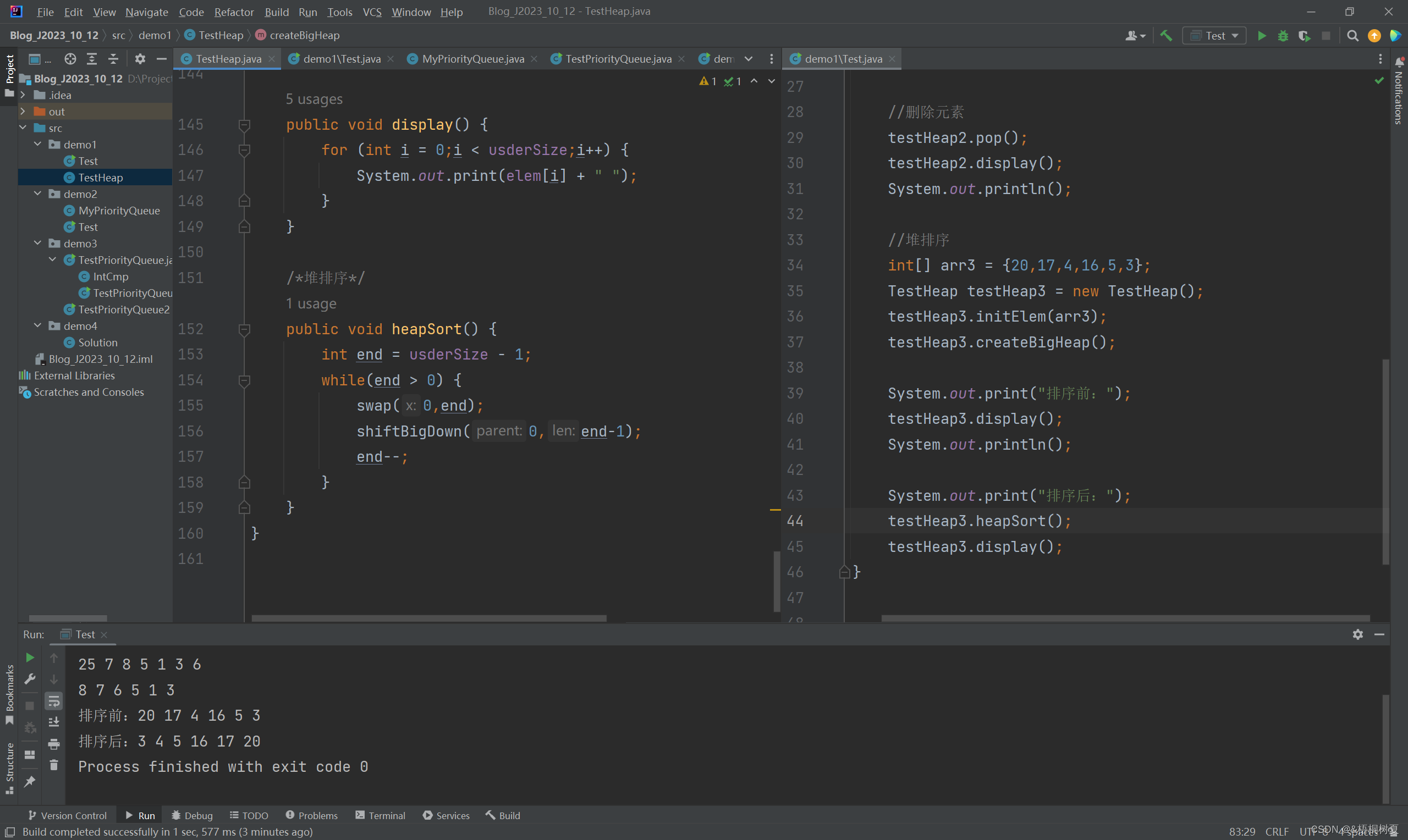
代码示例:
public void heapSort() {int end = usderSize - 1;while(end > 0) {swap(0,end);shiftBigDown(0,end-1);end--;}}public void shiftBigDown(int parent,int len) {//左孩子int child = 2 * parent + 1;while(child < len) {//判断是否存在右孩子 且右孩子和左孩子哪个更大,大的为childif (child+1 < len && elem[child+1] > elem[child]) {child++;}//判断根节点和child的大小,若根节点大则结束遍历,否则交换两个节点if (elem[child] > elem[parent]) {swap(child, parent);parent = child;child = 2 * parent + 1;}else {break;}}}
相关文章:

数据结构 优先级队列(堆)
数据结构 优先级队列(堆) 文章目录 数据结构 优先级队列(堆)1. 优先级队列1.1 概念 2. 优先级队列的模拟实现2.1 堆的概念2.2 堆的存储方式2.3 堆的创建2.3.1 堆向下调整2.3.2 堆的创建2.3.3 建堆的时间复杂度 2.4 堆的插入与删除2.4.1 堆的插入2.4.2 堆的删除 2.5 用堆模拟实现…...

如何在edge浏览器中给PDF添加文字批注
我用的edge浏览器是目前最新版的(一般自动更新到最新版) 最近,我喜欢用edge浏览器查看PDF,节省电脑资源,快捷且方便。 但edge对PDF的标注种类较少,主要是划线和涂色,文字批注功能尚未出现在工具…...
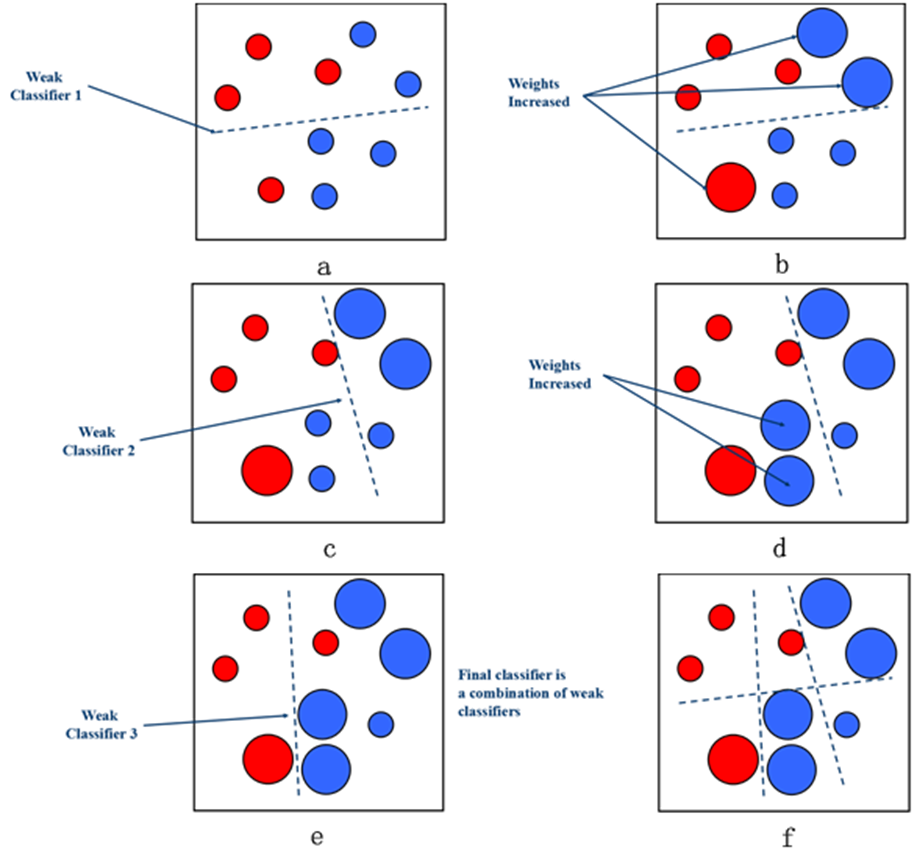
集成学习的小九九
集成学习(Ensemble Learning)是一种机器学习的方法,通过结合多个基本模型的预测结果来进行决策或预测。集成学习的目标是通过组合多个模型的优势,并弥补单个模型的不足,从而提高整体性能。 集成学习的主要策略 在集成…...
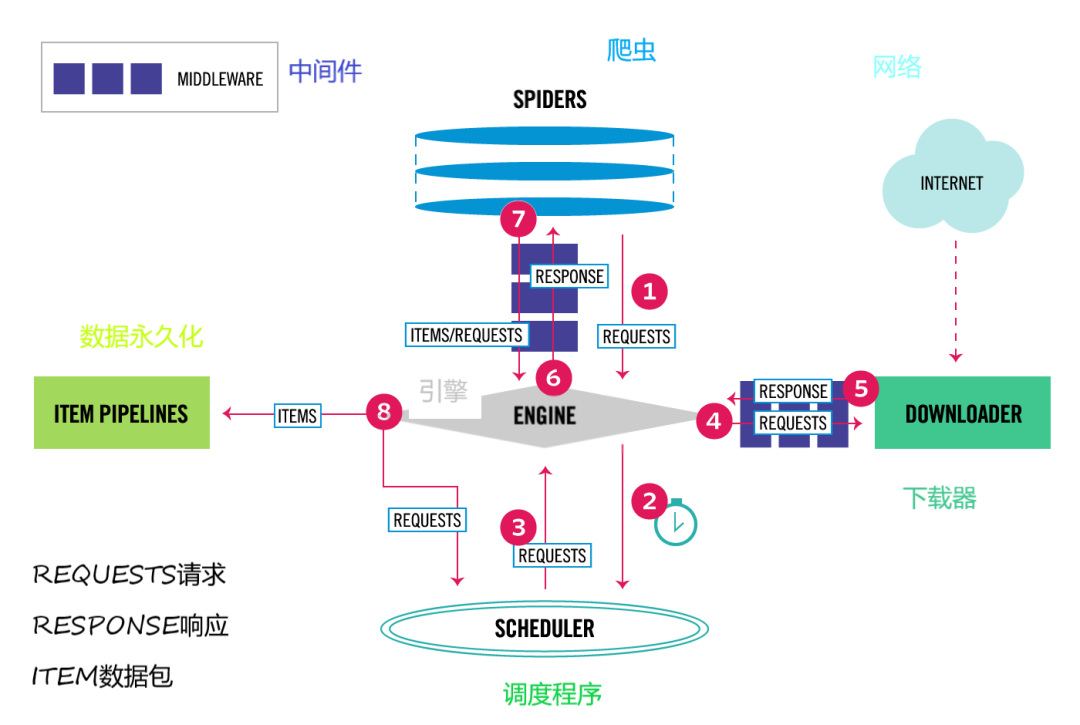
深入理解Scrapy
Scrapy是什么 An open source and collaborative framework for extracting the data you need from websites. In a fast, simple, yet extensible way. Scrapy是适用于Python的一个快速、简单、功能强大的web爬虫框架,通常用于抓取web站点并从页面中提取结构化的数…...
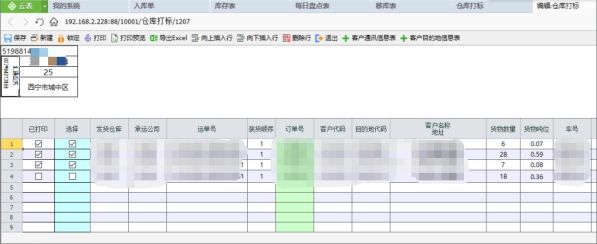
想做WMS仓库管理系统,找了好久才找到云表
公司内部仓库管理原方式均基于人工电子表格管理方式来实现收发存管理,没有流程化管理,无法保证数据的准确性和及时性,同时现场操作和数据核对会出现不同步的情况,无法提高仓库的运作效率,因此,我们基于云表…...
公司销售个人号如何管理?
微信管理系统可以帮助企业解决哪些问题呢? 一、解决聊天记录监管问题 1.聊天记录的保存,让公司的管理者可以随时查看公司任意销售与客户的聊天记录,不用一个一个员工逐一去看,方便管理; 2.敏感词监控,管理者…...

COLE HERSEE 48408 工业4.0、制造业X和元宇宙
COLE HERSEE 48408 工业4.0、制造业X和元宇宙 需要数据来释放工业4.0的全部潜力——价值链中的所有公司都可以访问大量数据。一个新的互联数据生态系统旨在提供解决方案:制造业x。 在德国联邦经济事务和气候行动部以及BDI、VDMA和ZVEI贸易协会的密切合作下,实施制…...
【Vue基础-数字大屏】加载动漫效果
一、需求描述 当网页正在加载而处于空白页面状态时,可以在该页面上显示加载动画提示。 二、步骤代码 1、全局下载npm install -g json-server npm install -g json-server 2、在src目录下新建文件夹mock,新建文件data.json存放模拟数据 {"one&…...

CSS 样式简写
在CSS中有许多简写的样式,它们被广泛使用。简写最好按照如下顺序进行书写 font font: font-style font-weight font-size/line-height font-familyfont-style italic//斜体 normal//正常字体(默认)font-weight 一般填写数字 400 normal(默认值) 700 bold(默认值)f…...

SQL Server创建数据库
简单创建写法 默认初始大小为5MB,增长速度为2MB create database DBTEST自定义 用户创建的数据库都被存放在sys.database中,每个数据库在表中占一行,name字段存放的数据库的名称,具体字段可以看此博客sys.database系统表详细说明 所以判断…...
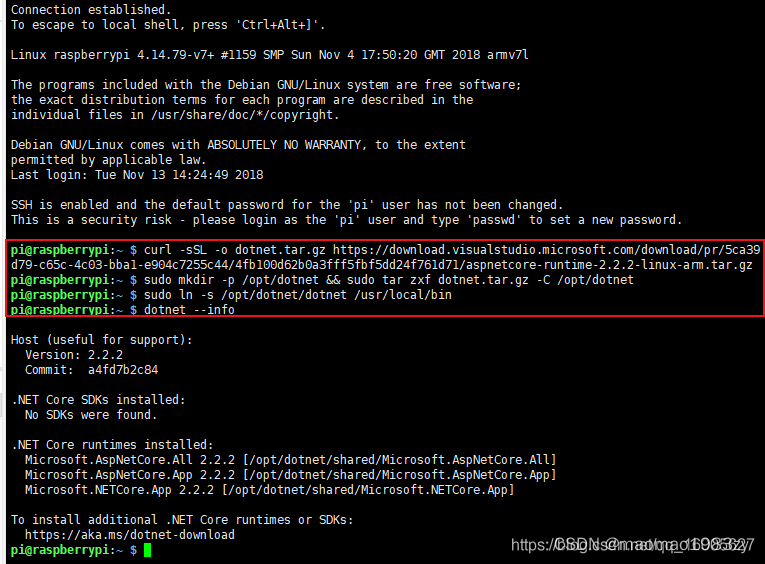
树莓派安装.NET 6.0
首先安装.Net Core依赖(未使用) sudo apt install -y libunwind8 libunwind8-dev gettext libicu-dev liblttng-ust-dev libcurl4 libcurl4-openssl-dev libssl-dev uuid-dev unzip libgdiplus libc6-dev libkrb5-3 需要安装的依赖微软官方文档已经列出…...

小华HC32F448串口使用
目录 1. 串口GPIO配置 2. 串口波特率配置 3. 串口接收超时配置 4. 串口中断注册 5. 串口初始化 6. 串口数据接收处理 7. DMA接收配置和处理 1. 串口GPIO配置 端口号和Pin脚号跟STM32没什么区别。 串口复用功能跟STM32大不一样。 如下图,选自HC32F448 表 2…...

Redis实现简易消息队列的三种方式
Redis实现简易消息队列的三种方式 消息队列简介 消息队列是一种用于在计算机系统中传递和处理数据的重要工具。如果你完全不了解消息队列,不用担心,我将尽力以简单明了的方式来解释它。 首先,想象一下你正在玩一个游戏,而游戏中…...
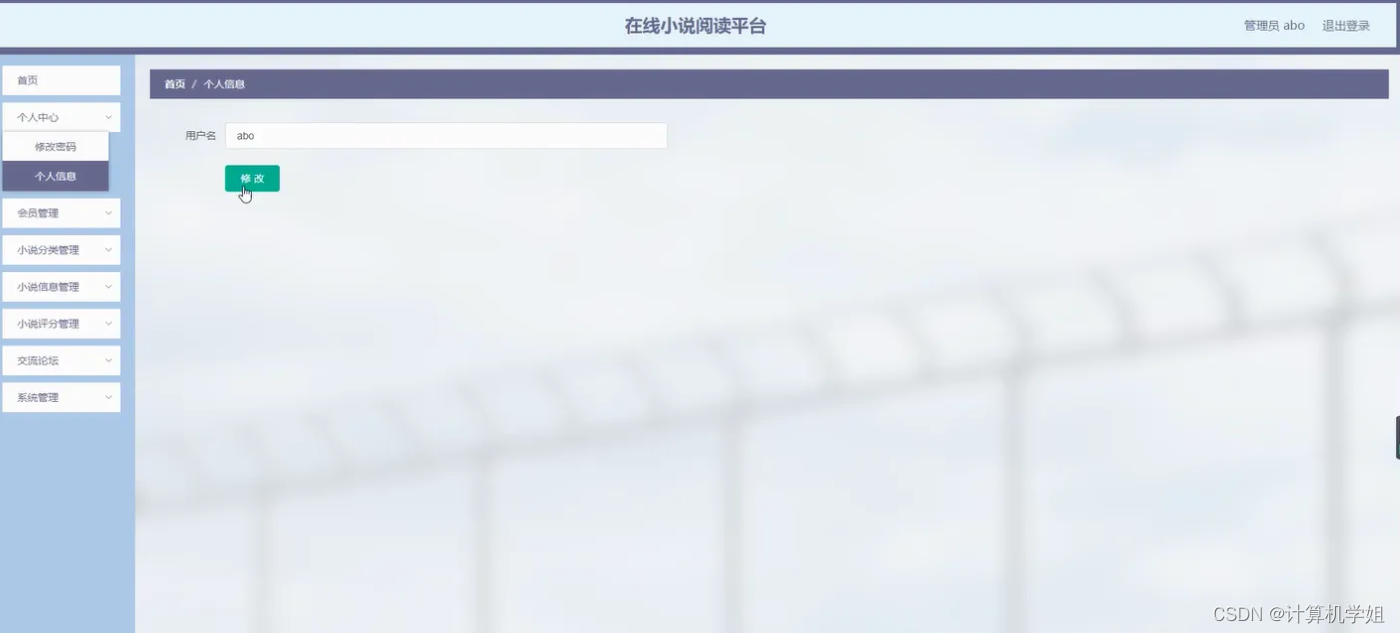
基于SpringBoot的在线小说阅读平台系统
基于SpringBoot的在线小说阅读平台系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringBootMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 主页 个人中心 登录界面 管理员界面 摘要 基于Spring Boot的在线小说阅读…...

uniapp h5 MD5加密
文章目录 1.当使用 CryptoJS 进行 MD5 加密时,你需要先引入 CryptoJS 库并确保它已经正确安装。下面是一个更详细的示例代码:2.然后,在需要使用 MD5 加密的地方,引入 CryptoJS 代码库:3.接下来,我们定义一个…...
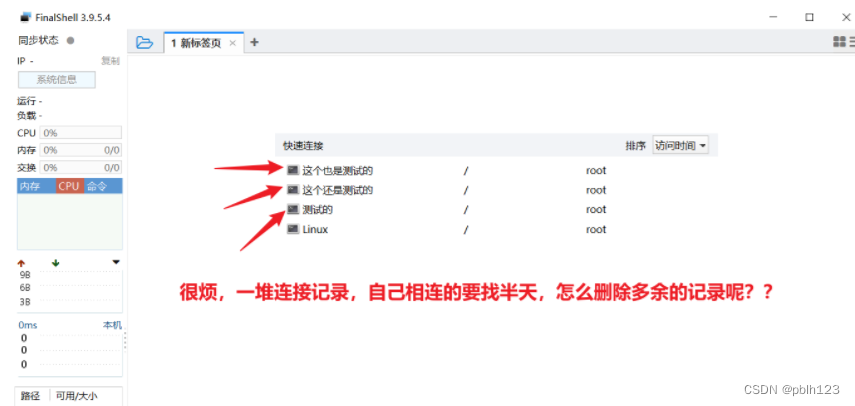
2023_Spark_实验十八:安装FinalShell
下载安装包 链接:https://pan.baidu.com/s/14cOJDcezzuwUYowPsOA-sg?pwd6htc 提取码:6htc 下载文件名称:FinalShell.zip 二、安装 三、启动FinalShell 四、连接远程 linux 服务器 先确保linux系统已经开启,不然连接不上 左边…...

文件服务器管理服务器怎么设置
文件服务器是一种提供文件存储和共享服务的服务器,它可以方便企业内部的员工共享文件,提高工作效率。为了更好地管理和维护文件服务器,需要对其进行合理的设置。下面小编将介绍文件服务器管理服务器的基本设置方法。 一、选择合适的操作系统 …...

LeetCode每日一题——Single Number
文章目录 一、题目二、题解 一、题目 136. Single Number Given a non-empty array of integers nums, every element appears twice except for one. Find that single one. You must implement a solution with a linear runtime complexity and use only constant extra …...
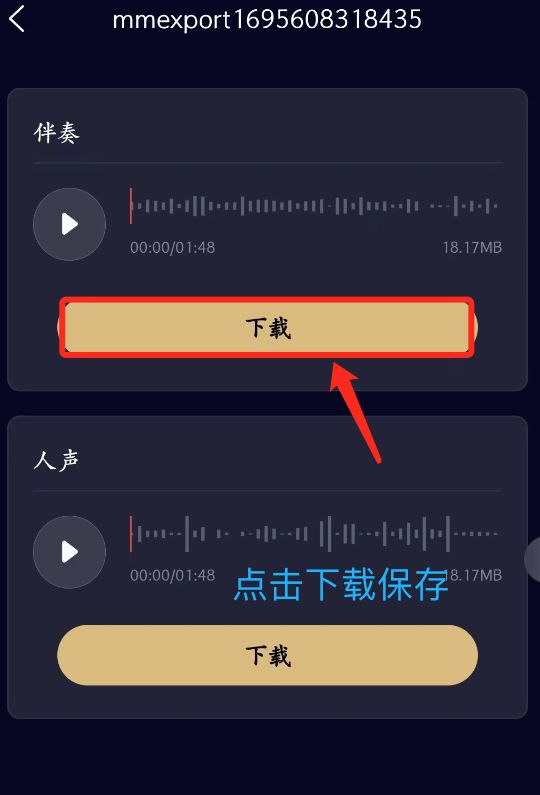
有什么手机软件能分离人声和音乐?
很多人在制作混剪视频,需要二次创作的时候,就经常会把人声分离、背景音乐伴奏提取出来,然后重新加入自己的创意跟想法。下面就一起来看看如何用手机软件分离人声和音乐的吧! 音分轨 一款可以分离人声和背景音乐的手机软件&#x…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...