数据结构之基:从根儿上了解数据结构的特性
学好数据结构,就等于成功了一半。
程序是对现实的模拟,现实是由时间和空间组成的,高效的人都是用最少的时间、最少的空间来做最伟大的事,程序亦是如此。我们要选择最合理的算法和最合理的数据结构,来写最好的代码,这也正是时间复杂度和空间复杂度的要求。
所以,学好数据结构,选择合理的数据结构,降低时空复杂度,就等于成功了一半。
我们可以将数据结构分为两大部分:线性数据结构和非线性数据结构。
线性数据结构:数据元素之间的关系是一对一的。非线性数据结构:数据元素之间的关系不是一对一的。
线性数据结构
数据元素之间的关系是一对一的。可以简单地记忆为:一根绳子不分叉!
这是嘛意思呢?
可以这么理解:我有一根绳子,上面打了好多结,我随便找到一个结点,不管往哪一端捋,都只能找到一个点,除非到头了导致没结点了。说白了就是:这根绳子没有分叉。
比如我们生活中的排队,就是这个模型。你前后最多都只有一个人,也就是:一对一的。
这个模型有很多衍生物,我们来逐个看下。
1. 顺序表
顺序表是紧密相邻的线性数据结构。便于查找元素,不便于插入和删除元素。
也就是说:顺序表的所有元素都是一个挨一个的。
比如军训时候的排队,所有人都在操场内;再比如核酸检测时的排队,所有人都在检测亭附近;前一个人挨着后一个人,紧密相邻。
所以,顺序表的特点就是:相邻!
这样就有一个明显的特点,因为我们彼此是挨着的,那么就等于排好了队。那么,我只要知道某个人的位置,就能找到他。
那么,我们就可以根据这个特点给每个元素定个编号,然后根据编号直接找到对应的元素。如下图所示:

我们要找第 ii 个人,也就是 aiai,直接去第 i−1i−1 位置即可,这样非常快,不用一个一个数。
那有人就说了,既然这么方便,我们直接全部用顺序表不就行了吗?不行!
这样找着是很快,但是,你发现了吗,如果少了一个元素,后面的所有元素都要往前挪一步;插入一个元素,后面所有元素都要往后挪一步。就像排队,有人插队和离队,后面所有人都要挪一步。
那么,能不能不挪呢?如果不挪,就留了个空位,那么空位前后的人就没有相邻元素了,那么就从空位开始断开了,那么就不是顺序表了。所以不行,必须挪!
综上所述,顺序表的特点就是:便于查找元素,不便于插入和删除元素!
那么,有没有啥法子能插入和删除时候不挪呢?这样就可以专门用来针对低素质群体了。
有,链表!
2. 链表
链表是非直接相邻的顺序表。便于插入删除,不便于查找。
链表跟顺序表是一对“杠精”,只要记住顺序表的特点,反过来就是链表的特点。顺序表的元素是一个挨一个的,链表就是不挨的。
有人可能会问了:这不对啊,不挨着怎么找到前一个或者后一个元素,要是找不到,就不是线性表了。
可以找到,就是要费点劲。
比如:我在北京,我爸爸在上海,不相邻,我能找到他吗?能啊,我直接根据地址开车过去就行了,虽然费劲,但是也能找到啊,并且这个地址也只能找到他啊。这也满足:一对一的关系。
这找得也太费劲了,确实费劲。有人要找我,但他只有我爷爷的地址,就先找到了我爷爷,问他要了我爸的地址,然后找到了我爸要了我的地址,最后根据地址找到了我。
从这里可以看到,链表的查找步骤不是直接报个序号就行的,而是需要从头开始挨个往下找,所以查找费劲,也就不便于查找。
那么,为什么要这么设计呢?因为这样便于插入和删除。比如有一天,我爸去了国外,那么他只要把我的地址给我爷爷就行了,我和我爷爷都不需要搬家,这样找我的人,还是按照之前的步骤就行;如果有一天我爸回来了,那么他把他自己的地址给我爷爷,然后我把我自己的地址给他,就行了,仍然不需要搬家。如果是顺序表就惨了,估计搬家都搬吐血了。
从这里我们可以看到,链表的设计是不需要相邻的,它通过上一个元素持有下一个元素的地址来找到下一个元素,插入/删除时只需要改变地址即可,不需要挪动位置。这样非常便于插入和删除,但是不便于查找。
这样通过地址连起来,就像一条“链”一样,如下图所示:

如果我们删除了 aiai,我们只需要将 ai−1ai−1 指向的地址改成 ai+1ai+1 即可。插入元素同理。
所以,链表的特点是:便于插入删除, 不便于查找。
3. 栈
栈是先进后出(
FILO)的线性结构。
栈是一种抽象的数据结构,它只要求元素满足先进后出,不要求你是怎么存放的。
比如只有一个门的公交车,第一个进去的最后才能出来;比如冰柜里的雪糕,第一个放进去的最后才被取出来;再比如碗里的饺子,第一个放进去的最后才被吃掉。
这些都有一个特点:只有一个口!因为只有一个口,所以导致最先进去的最后才出来,所以就叫先进后出,或者叫作 FILO(First In Last Out)。
那么,这有啥用呢?难不成就是专门用来模拟吃饺子的?非也!
因为栈是先进后出的,所以特别适合用来模拟历史的回溯,也就是说,逆流而上追溯历史,将历史“倒放”一遍。
历史的回放?这是啥?比如我们打开浏览器,打开一个个页面,我们关闭的一定是最后打开的,换句话说:最先打开的反而最后关闭。也就是说,如果我们打开的顺序是:A->B->C->D,那么我们关闭的顺序就是 D->C->B->A。
这给我们的感觉就是:将历史记录倒放了一遍。这正是栈的特点。
历史明明是“前天->昨天->今天”这样过来的,但是我们回到过去的话,却是“今天->昨天->前天”这样经过的,这就是对历史的回溯。
栈最常用的地方就是计算机的函数调用,不管何种语言,最先被调用的一定最后返回,比如:
functionA() {functionB();
}functionB() {functionC();
}
- 调用顺序是:
functionA()->functionB()->functionC()。 - 返回顺序是:
functiuonC()->functioB()->functionA()。
functionC()最后被调用,却最先被执行完,然后把结果返回给functionB(),functionB()再执行完毕返回,把结果返回给functionA()。
这就是栈最常用的地方,所以我们经常说函数栈,也就是这个道理。
其实我们可以广义地概括一下栈的使用场景:具有对称性。凡是具有对称性要求的场景,都优先考虑使用栈。
比如上面的页面返回例子,A->B->C->D 和 D->C->B-A,这是以 D 为对称轴左右对称的。上面的函数调用,也是以functionC()为对称轴左右对称的。
换句话说:FILO 就是以最后进来(最先出去)的那个为对称轴左右对称的,凡是有这种要求的,都以优先考虑栈。
4. 队列
队列是先进先出(
FIFO)的线性结构。
队列是一种抽象的数据结构,它要求元素满足先进先出,不要求元素怎么存放。
比如两个门的公交车,前面进、后面出,那么先进入的人就会先出来;再比如汽车排队隧道,先进入的先出来。
它们也都有一个特点:两个口!因为两个口,一个进一个出,那么先进去的肯定先跑到出口,所以就叫先进先出,或者叫作 FIFO(First In First Out)。
可以看到,队列跟栈相反,更适合人们的思维,因为它是公平的!
它可以用于模拟日常的大部分操作,比如下载,先点击的就先下载,只有前面的下载完了才轮到后面的;再比如,12306 买票的候补,先点击候补的优先出票。
因为队列是先进先出的,所以就特别适合对历史的回放。也就是说,按照历史顺序,将历史“重新演绎一遍”。
比如:我们开发一个直播间,先进直播间的人肯定排在前面。这时候就可以使用队列。
因为队列是先进先出的,也是符合人们正常思维的,所以,凡是不需要使用栈的地方,都可以使用队列。
非线性数据结构
数据元素之间的关系是一对多,或者多对多的。
非线性数据结构的关系可能是一对多,或者是多对多。一对多的我们称为树;多对多的我们称为图。
1. 树
树是一对多的数据结构。适合有层级关系的场景。
我们知道,树只有一个根,但是却有多个分支,每个分支又有多个分支。这特别适合用来模拟分层的场景,比如组织结构图、大纲图,还有脑图。
最常见的场景就是分页了。
比如:从一亿个人中,找到一个名字叫张三的人(假设名字都不重复),怎么找呢?一个一个去对比名字是否叫张三吗?这太费劲了。
我们可以这样做:
- 先按照名字个数分组,两个字名字的分到 A 组,三个字名字的分到 B 组,四个字名字的分到 C 组。
- 针对每一组,再按照姓氏分,姓王的分到王组,姓张的分到张组。
- 然后针对每个姓氏组,再按照名字的笔画分组,“三”有 3 笔,就被分到 3 组。
这样,我们就好找了。张三,两个字,去 A 组;姓张,去张组;名字是 3 笔,去 3 组。也就是,A 组的张组的 3 组。这里只有几千个人了,很好找了。
这里的整个一亿人就是一棵树,A 组、B 组、C 组分别是主枝干,王组、张组是次一级枝干,1 组、2 组、3 组又是次一级枝干,每个人都是一片叶子。
可以看到,有明显的层次关系,这样划分得更清晰,也更好找。
再比如,书的目录、部门的组织关系,等等,都很适合用树来表示。
到这里,我们总结下树的特点:一对多,有层级关系,适合分页。
2. 图
图是多对多的数据结构。适合没有层级的网状关系。
既然树适合有层级的场景,那么没有层级的呢,就可以用图了。
比如:手机联系人,我有我家人的、我朋友的,家人又有家人的,家人又有他们的朋友的……如此,就形成了一张大网,这张网里的所有人都是平等关系,又都是多对多的,这就适合用图来表示了。
假如我们要做一个城市的地图,或者要做一个朋友圈关系网,我们就可以采用图。
有人说,图是平级关系,那么我们的城市地图有拥挤程度,朋友圈也有重要朋友和不重要朋友,怎么表示呢?这个就可以使用加权图了,这是更详细的划分了,本章我们不做过多介绍。
这里说的“层级”,不是关系的重要程度,而是是否存在着主次关系,如果有了主次关系,那就不适合使用图了。
图的使用除了日常的模型模拟之外,还有路径规划、拓扑排序等很多场景,我们后面会细讲。
总结
本章从整体讲解了数据结构的划分,以及它们的特点和使用场景,有点流水账的味道。我们再来梳理和回顾一下。
- 线性数据结构:元素之间是一对一的关系。
- 非线性数据结构:元素之间是一对多或多对多的关系。
- 顺序表:紧密相邻的线性数据结构,便于查找,不便于插入删除。
- 链表:不相邻的线性数据结构,便于插入删除,不便于查找。
- 栈:先入后出的线性数据结构,适合对历史的回溯。
- 队列:先入先出的线性数据结构,适合对历史的回放。
- 树:一对多的非线性数据结构,适合有层级关系的场景。
- 图:多对多的非线性数据结构,适合无层级关系的场景。
我们这部分讲的内容都是抽象的,并不涉及具体的实现,因为我们只有先从顶层了解了它们的概念和特点后,再带着这些已有理解去看具体实现会有更深刻的印象,记得也更牢。后面我们就从具体的实现来看一下每一种数据结构的具体使用场景以及在代码中的精彩表现。
程序员的必修课 - 奔波儿灞取经 - 掘金小册数据结构+计算机网络+操作系统+设计模式,软硬兼修,深入浅出带你夯实程序员基本功。「程序员的必修课」由奔波儿灞取经撰写,610人购买![]() https://s.juejin.cn/ds/BoPu7q4/
https://s.juejin.cn/ds/BoPu7q4/
相关文章:
数据结构之基:从根儿上了解数据结构的特性
学好数据结构,就等于成功了一半。 程序是对现实的模拟,现实是由时间和空间组成的,高效的人都是用最少的时间、最少的空间来做最伟大的事,程序亦是如此。我们要选择最合理的算法和最合理的数据结构,来写最好的代码&…...

C++ 枚举详解
C 枚举详解 C 枚举类型详解 枚举类型的定义格式为: enum <类型名> {<枚举常量表>};关键字enum——指明其后的标识符是一个枚举类型的名字枚举常量表——由枚举常量构成。“枚举常量"或称"枚举成员”,是以标识符形式表示的整型量&…...

【vue3】ref , reactive ,toRef ,toRefs 使用和理解
这篇文章是基于理解写的,仅助于理解,如有任何错误之处,感谢指正! 文章目录一.ref的使用1. ref的功能主要有两个:2.使用ref注意事项二.reactive的使用三.使用ref 和 reactive 实现双向数据绑定四.toRef 和 toRefs 的使用…...
fastadmin:如何点击按钮弹出存在的指定页面的弹窗
样式:方法一:直接使用超链接进行操作{:url(popup/purchase/itemno)}:表示地址信息btn-dialog:表示弹窗<a href"{:url(popup/purchase/itemno)}" title"跳转第三方" class"btn btn-success btn-dialog…...
【storybook】你需要一款能在独立环境下开发组件并生成可视化控件文档的框架吗?(三)
storybook插件addons核心插件插件APIargTypes写文档组件注释法MDX生成在线可视化UI文档上一篇: https://blog.csdn.net/tuzi007a/article/details/129194267插件addons 插件用于增强storybook的UI功能。 核心插件 storybook/addon-essentials 它几乎控制了整个s…...
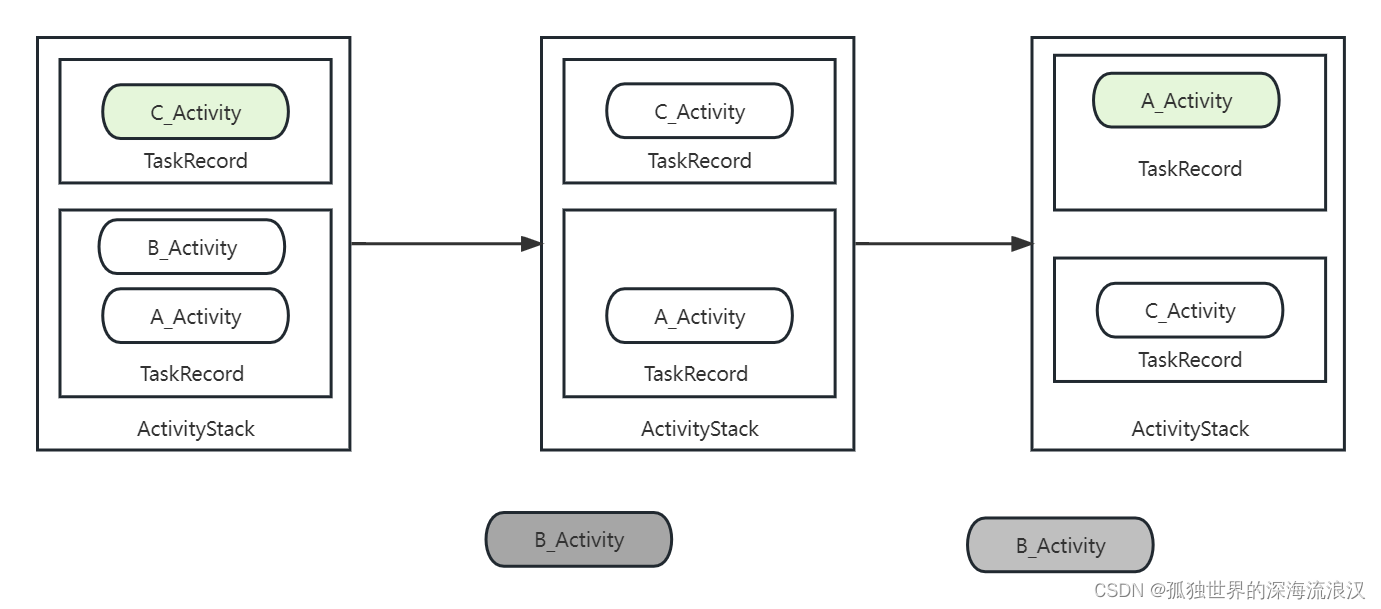
Android源码分析 —— Activity栈管理(基于Android8)
0. 写在前面 本文基于 Android8.0源码,和Android9.0大同小异,但和Android10.0差别非常大!新版改用ATM来管理Activity的启动,Activity的生命周期也通过XXXItem来管理。由于我分析的Activity启动流程就是基于Android8/9的ÿ…...
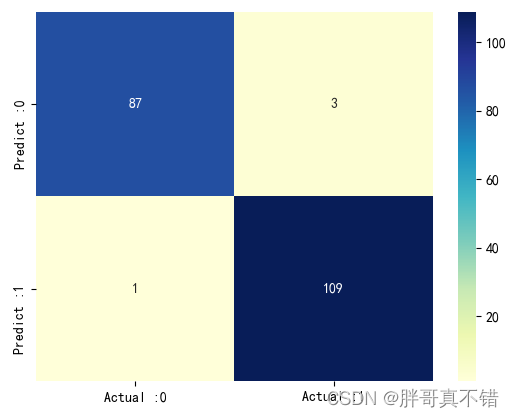
Python实现贝叶斯优化器(Bayes_opt)优化支持向量机分类模型(SVC算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。1.项目背景贝叶斯优化器(BayesianOptimization) 是一种黑盒子优化器,用来寻找最优参数。贝叶斯优化器是基…...

【华为OD机试模拟题】用 C++ 实现 - 分积木(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

FFmpeg/OpenCV 实现全屏斜体水印
实现思路 🤔 基于ffmpeg,画布的方式,创建画布 -> 水印 -> 旋转 -> 抠图 -> 叠加到图像上基于ffmpeg,旋转图片的方式,填充 -> 水印 -> 顺时针旋转 -> 逆时针旋转 -> 截图基于opencvÿ…...

Calendar计算两个时间之间相差几个月
目录说明说明 计算两个时间之间相差几个月: public int getMonth(String startDt, String endDt) { int month 0;try {SimpleDateFormat sdf new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");Calendar satrt Calendar.getInstance();Calendar end Cal…...
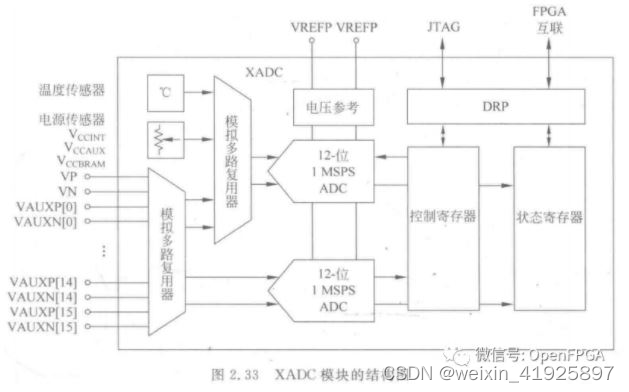
FPGA基础知识
FPGA是在PAL、PLA和CPLD等可编程器件的基础上进一步发展起来的一种更复杂的可编程逻辑器件。它是ASIC领域中的一种半定制电路,既解决了定制电路的不足,又克服了原有可编程器件门电路有限的缺点。 由于FPGA需要被反复烧写,它实现组合逻辑的基…...

C语言运算符逻辑运算符位运算符
逻辑运算符 下表显示了 C 语言支持的所有关系逻辑运算符。假设变量 A 的值为 1,变量 B 的值为 0,则: 运算符 描述 实例 && 称为逻辑与运算符。如果两个操作数都非零,则条件为真。 (A && B) 为假。 || 称为逻辑…...
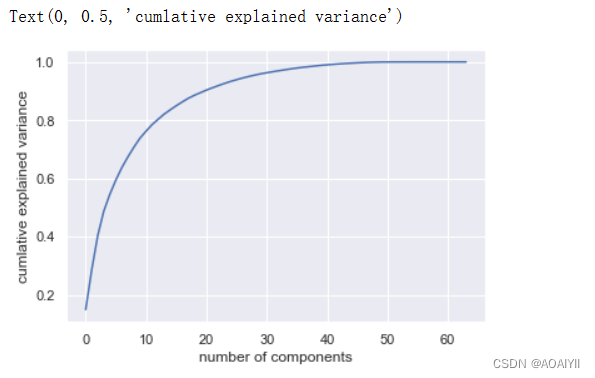
机器学习:基于主成分分析(PCA)对数据降维
机器学习:基于主成分分析(PCA)对数据降维 作者:AOAIYI 作者简介:Python领域新星作者、多项比赛获奖者:AOAIYI首页 😊😊😊如果觉得文章不错或能帮助到你学习,可…...
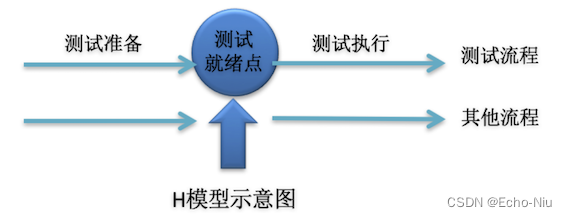
软件测试之测试模型
软件测试的发展 1960年代是调试时期(测试即调试) 1960年 - 1978年 论证时期(软件测试是验证软件是正确的)和 1979年 - 1982年 破坏性测试时期(为了发现错误而执行程序的过程) 1983年起,软件测…...
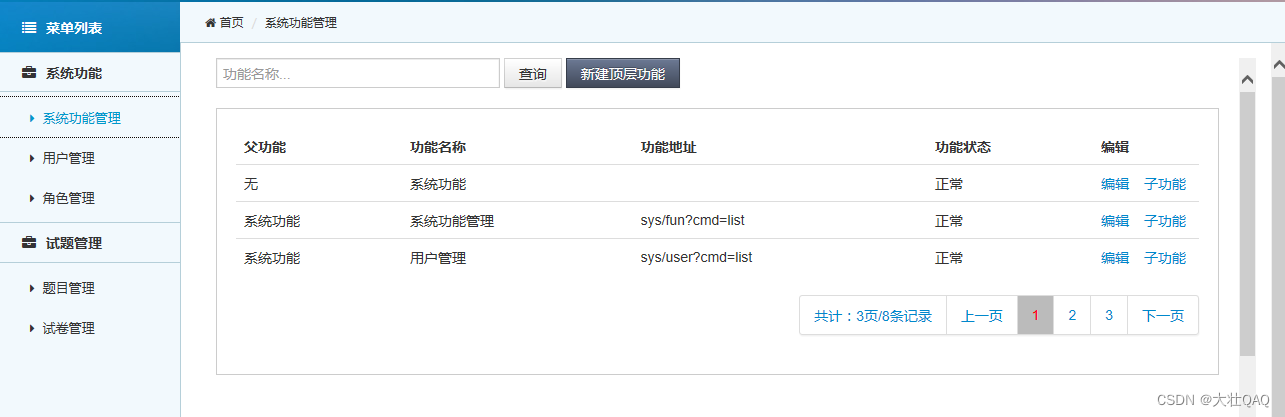
【项目精选】网络考试系统的设计与实现(源码+视频+论文)
点击下载源码 网络考试系统主要用于实现高校在线考试,基本功能包括:自动组卷、试卷发布、试卷批阅、试卷成绩统计等。本系统结构如下: (1)学生端: 登录模块:登录功能; 网络考试模块…...

Python近红外光谱分析与机器学习、深度学习方法融合实践技术
、 第一n入门基础【理论讲解与案 1、Python环境搭建( 下载、安装与版本选择)。 2、如何选择Python编辑器?(IDLE、Notepad、PyCharm、Jupyter…) 3、Python基础(数据类型和变量、字符串和编码、list和tu…...

实例7:树莓派呼吸灯
实例7:树莓派呼吸灯 实验目的 通过背景知识学习,了解digital与analog的区别。通过GPIO对外部LED灯进行呼吸控制,熟悉PWM技术。 实验要求 通过python编程,用GPIO控制LED灯,使之亮度逐渐增大,随后减小&am…...
java 接口 详解
目录 一、概述 1.介绍 : 2.定义 : 二、特点 1.接口成员变量的特点 : 2.接口成员方法的特点 : 3.接口构造方法的特点 : 4.接口创建对象的特点 : 5.接口继承关系的特点 : 三、应用 : 1.情景 : 2.多态 : ①多态的传递性 : ②关于接口的多态参数和多态…...
用 Visual Studio 升级 .NET 项目
现在,你已可以使用 Visual Studio 将所有 .NET 应用程序升级到最新版本的 .NET!这一功能可以从 Visual Studio 扩展包中获取,它会升级你的 .NET Framework 或 .NET Core 网页和桌面应用程序。一些项目类型仍正在开发中并将在不久的未来推出&a…...

JavaWeb中FilterListener的神奇作用
文章目录1,Filter1.1 Filter概述1.2 Filter快速入门1.2.1 开发步骤1.3 Filter执行流程1.4 Filter拦截路径配置1.5 过滤器链1.5.1 概述1.5.2 代码演示1.5.3 问题2,Listener2.1 概述2.2 分类2.3 代码演示最后说一句1,Filter 1.1 Filter概述 F…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
