算法训练营 day42 动态规划 理论基础 斐波那契数 爬楼梯 使用最小花费爬楼梯
算法训练营 day42 动态规划 理论基础 斐波那契数 爬楼梯 使用最小花费爬楼梯
理论基础
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的,
规是由前一个状态推导出来的,而贪心是局部直接选最优的,
状态转移公式(递推公式)是很重要,但动规不仅仅只有递推公式。
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
斐波那契数
509. 斐波那契数 - 力扣(LeetCode)
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。
这里我们要用一个一维dp数组来保存递归的结果
-
确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
-
确定递推公式
题目已经把递推公式直接给我们了:状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
-
dp数组如何初始化
题目中把如何初始化也直接给我们了
-
确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
-
举例推导dp数组
class Solution {public int fib(int n) {if(n<=1) return n;int[] dp = new int[n+1];dp[0] = 0;dp[1] = 1;for (int i = 2; i <=n; i++) {dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
}
爬楼梯
70. 爬楼梯 - 力扣(LeetCode)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
动规五部曲:
定义一个一维数组来记录不同楼层的状态
-
确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方法
-
确定递推公式
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
-
dp数组如何初始化
其实这么争论下去没有意义,大部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过,然后就往结果上靠去解释dp[0] = 1。
所以我的原则是:不考虑dp[0]如何初始化,只初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推,这样才符合dp[i]的定义。
-
确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的
-
举例推导dp数组
class Solution {public int climbStairs(int n) {if (n<2) return n;int[] dp = new int[n+1];dp[1] = 1;dp[2] = 2;for (int i = 3; i < dp.length ; i++) {dp[i] = dp[i-2]+dp[i-1];}return dp[n];}
}
使用最小花费爬楼梯
746. 使用最小花费爬楼梯 - 力扣(LeetCode)
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
-
确定dp数组以及下标的含义
本题只需要一个一维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
2. 确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
-
dp数组如何初始化
看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
-
确定遍历顺序
因为是模拟台阶,而且dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
-
举例推导dp数组
class Solution {public int minCostClimbingStairs(int[] cost) {if (cost.length==0) return 0;if (cost.length==1) return cost[0];int[] dp = new int[cost.length+1];dp[0] = 0;dp[1] = 0;for (int i = 2; i < dp.length; i++) {dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.length];}
}
相关文章:

算法训练营 day42 动态规划 理论基础 斐波那契数 爬楼梯 使用最小花费爬楼梯
算法训练营 day42 动态规划 理论基础 斐波那契数 爬楼梯 使用最小花费爬楼梯 理论基础 动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。 所以动态规划中每一个状…...

MySQL8 创建用户,设置修改密码,授权
MySQL8 创建用户,设置修改密码,授权 MySQL5.7可以 (创建用户,设置密码,授权) 一步到位 👇 GRANT ALL PRIVILEGES ON *.* TO 用户名% IDENTIFIED BY 密码 WITH GRANT OPTION👆这样的语句在MySQL8.0中行不通, 必须 创设和授权 分步执行👇 CR…...

MySQL —— 内置函数
目录 内置函数 一、日期函数 二、字符串函数 三、数学函数 四、其他函数 内置函数 一、日期函数 函数名称描述current_date()获取当前日期current_time()获取当前时间current_timestamp()获取当前时间戳now()获取当前日期时间date(datetime)获取datetime参数的日期部分d…...

Mybatis框架(全部基础知识)
👌 棒棒有言:也许我一直照着别人的方向飞,可是这次,我想要用我的方式飞翔一次!人生,既要淡,又要有味。凡事不必太在意,一切随缘,缘深多聚聚,缘浅随它去。凡事…...

pixhawk2.4.8使用调试记录—APM固件
目录一、硬件准备二、APM固件、MP地面站下载三、地面站配置1 刷固件2 机架选择3 加速度计校准4 指南针校准5 遥控器校准6 飞行模式7 紧急断电&无头模式8 基础参数设置9 电流计校准10 电调校准11 起飞前检查(每一项都非常重要)12 飞行经验四、遇到的问…...
终于进了字节,记录一下我作为一名测试员磕磕碰碰的三个月找工作经历...
我是裸辞后重新找工作的,从去年到今年,前前后后花了大概三个月,大大小小参加了几百场面试。不是我说,作为一名测试员是真的挺难的,不过很庆幸自己最后拿到了字节的offer,今天在这里做一下记录吧,…...

基于PYTHON django四川旅游景点推荐系统
摘 要基于四川旅游景点推荐系统的设计与实现是一个专为四川旅游景点为用户打造的旅游网站。该课题基于网站比较流行的Python 语言系统架构,B/S三层结构模式,通过Maven项目管理工具进行Jar包版本的控制。本系统用户可以发布个人游记,查看景点使用户达到良…...

MySql服务多版本之间的切换
从网上总结的经验,然后根据自己所遇到的问题合并记录一下,方便日后再次需要用到 MySql服务多版本同时运行 步骤 1、如果你电脑上已经有一个mysql版本,例如mysql-5.7.39-winx64,它占据了3306端口。此时如果你想下仔另一版本&…...

嵌入式开发:通过嵌入式虚
嵌入式虚拟化为实现多核处理能力的优势提供了一种可扩展的机制。嵌入式应用中的虚拟化与其企业和桌面应用有许多共同之处。独特的嵌入式使用案例和专业的底层技术为嵌入式开发人员提供了优化性能和响应设计的新机会。在台式机、数据中心以及现在的嵌入式设计中采用多核技术可以…...

广州穗雅医院杨济安:了解症状表现 有效防治口腔黏膜下纤维化
“医生,我出现口干大半年时间,最近两月张嘴费劲,吃点辣的,嘴就刺疼刺疼的,这是怎么回事?”半年前,家住南沙的文先生走进广州穗雅医院口腔黏膜科如是说到。在科室杨济安主任的详细问诊与检查后&a…...
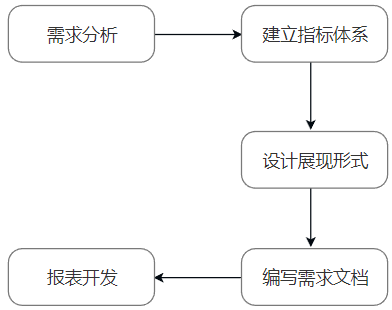
[数据分析] 数据指标体系搭建
在数据分析的学习过程中,我们通常会要求掌握以下两点: 1.理解数据,懂得从数据中发现业务指标(学会如何去看懂数据) 2.使用相关指标去分析数据,同时使用多个指标去分析一个问题(了解常见的指标) 当我们拿到数据(通常以Excel或者数据库方式去…...

Dubbo 源码分析 – 集群容错之 Cluster
3.2.2 FailbackClusterInvoker FailbackClusterInvoker 会在调用失败后,返回一个空结果给服务提供者。并通过定时任务对失败的调用进行重传,适合执行消息通知等操作。下面来看一下它的实现逻辑。 public class FailbackClusterInvoker<T> extend…...

Spring学习20230208-09
IOC底层原理 IOC概念 :面向对象编程中的一种设计原则,用来降低耦合度 通过控制反转,对象在被创建的时候,由一个调控系统内所有对象的外界实体将其所依赖的对象引用传递给他。可以说,依赖被注入到对象中。控制反转&…...
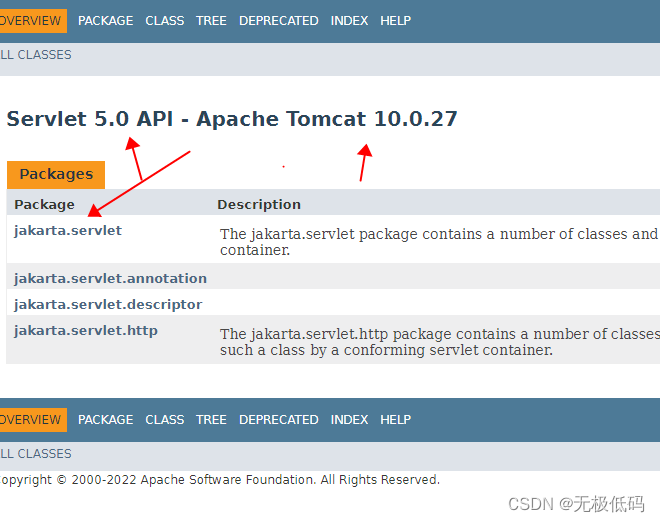
tomcat10部署报错WebStatFilter cannot be cast to jakarta.servlet.Filter
异常信息09-Feb-2023 23:08:49.946 严重 [main] org.apache.catalina.core.StandardContext.filterStart 启动过滤器异常[DruidWebStatFilter]java.lang.ClassCastException: com.alibaba.druid.support.http.WebStatFilter cannot be cast to jakarta.servlet.Filterat org.ap…...
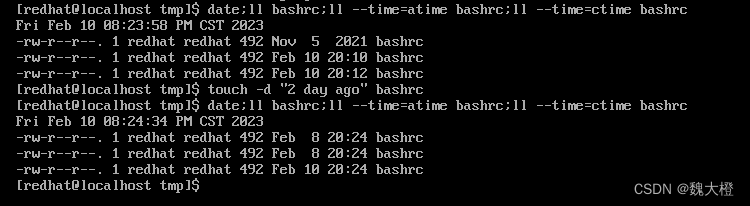
Linux修改文件时间或创建新文件:touch
每个文件在Linux下面都记录了许多的时间参数,其实是三个主要的变动时间 修改时间(modification time,mtime):当该文件的【内容数据】变更时,就会更新这个时间,内容数据是指文件的内容ÿ…...

原生微信小程序按需引入vant
vant Vant Weapp - 轻量、可靠的小程序 UI 组件库 1.npm安装 找到项目根目录 安装 # 通过 npm 安装 npm i vant/weapp -S --production# 通过 yarn 安装 yarn add vant/weapp --production# 安装 0.x 版本 npm i vant-weapp -S --production 2 .修改 app.json 将 app.jso…...
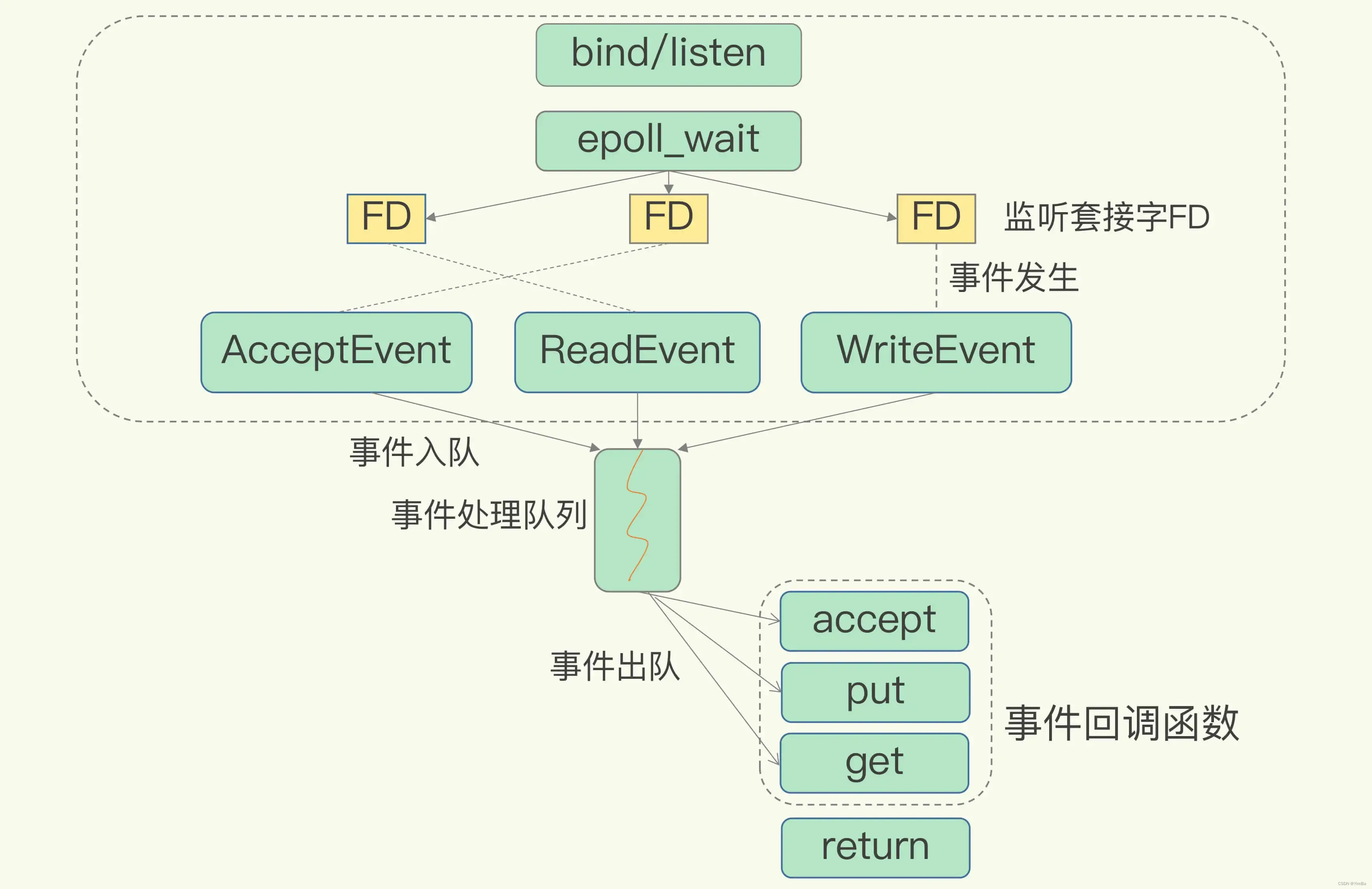
高性能IO模型:为什么单线程Redis能那么快?
我们通常说Redis是单线程,主要是指Redis的网络IO和键值对读写是由一个线程来完成的。这也是Redis对外提供键值存储服务的主要流程。 但redis的其他功能,比如持久化、异步删除、集群数据同步等,其实是由额外的线程执行的。 Redis为什么用单线…...

【数据集】中国各类水文专业常用数据集合集
1 水文气象数据 1.1 中国站点尺度天然径流量估算数据集(1961~2018年) 论文: J2022-High-quality reconstruction of China’s natural streamflow-缪驰远(北京师范大学地理科学学部) 研究内容:…...
落枕、肩颈酸痛,用磁疗就可缓解!
睡觉之前还是好好的,一觉醒来脖子莫名疼痛,转都转不了,有时候连肩膀和上肢都难受,很可能是“落枕”了。 落枕引起的肩颈疼痛与多种因素有关,如颈肩部肌肉的过度使用、不良的睡眠姿势或颈肩部受寒湿空气的侵袭ÿ…...

一文教会你如何选择远程桌面(五大主流远程软件全面讲解)
写在前面 作为程序员的我们,随时随地写代码改代码是我们的日常。刚回到家,就被老板、产品经理cue是常有的事。基于这种情况,一般都会随身携带电脑,随时备战,不过每天背着电脑上下班非常不方便。因此资深程序员的解决方…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...
