在动态规划的海洋中遨游(三)
前言:\textcolor{Green}{前言:}前言:
💞 好久没写题,有点生疏了。这也是给大家提一个醒,一定要一直坚持下去,哪怕每天只做一点点。💞
算法类别
- 一、算法介绍
- 原理
- 适用的情况
- 做题步骤
- 二、算法实例
- 1. 打家劫舍(一)
- 2. 打家劫舍(二)
- 3. 买卖股票的最好时机(一)
- 4. 买卖股票的最好时机(二)
- 总结归纳
一、算法介绍
原理
思想:将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法。按顺序求解子阶段,前面子问题的解为后面子问题的求解提供信息。
如果某一问题有很多重叠子问题,使用动态规划是最有效的。
动态规划中每一个状态一定是由上一个状态推导出来。
动态规划算法的基本思想是:将待求解的问题分解成若干个相互联系的子问题,先求解子问题,然后从这些子问题的解得到原问题的解;对于重复出现的子问题,只在第一次遇到的时候对它进行求解,并把答案保存起来,让以后再次遇到时直接引用答案,不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果。
适用的情况
- 最优化原理:如果问题的最优解所包含的子问题的解也是最优的,称该问题具有最优子结构,即满足最优化原理。
- 没有后效性:即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说:某状态以后的过程不会影响以前的状态,只与当前状态有关。
- 有重叠子问题:子问题之间是不独立的,一个子问题在下一个近阶段可能被多次遇到。(这条性质不是动态规划适用的必要条件,但是具备这条性质那么动态规划相对于其他算法就具备一定的优势)。
做题步骤
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
二、算法实例
1. 打家劫舍(一)
题目来源:\textcolor{OrangeRed}{题目来源:}题目来源:BM78 打家劫舍(一)
等级:中等\textcolor{OrangeRed}{等级:中等}等级:中等
👉题目描述
你是一个经验丰富的小偷,准备偷沿街的一排房间,每个房间都存有一定的现金,为了防止被发现,你不能偷相邻的两家,即,如果偷了第一家,就不能再偷第二家;如果偷了第二家,那么就不能偷第一家和第三家。
给定一个整数数组nums,数组中的元素表示每个房间存有的现金数额,请你计算在不被发现的前提下最多的偷窃金额。
数据范围:数组长度满足 1≤n≤2×1051≤n≤2×10^51≤n≤2×105,数组中每个值满足 1≤num[i]≤50001≤num[i]≤50001≤num[i]≤5000
示例1
输入:[1,2,3,4]
返回值:6
说明:最优方案是偷第 2,4 个房间
示例2
输入:[1,3,6]
返回值:7
说明:最优方案是偷第 1,3个房间
示例3
输入:[2,10,5]
返回值:10
说明:最优方案是偷第 2 个房间
👉代码编写
最好的办法是通过动态规划来进行。
如果单纯选择奇数家或者偶数家进行偷取,也可能发生问题。例如为了更多的钱可能会连续选择两家不偷。
👉👉方法1
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param nums int整型一维数组 * @return int整型*/public int rob (int[] nums) {// write code hereint len = nums.length;if (len <= 1) return nums[0];int[] dp = new int[len];dp[0] = nums[0];dp[1] = Math.max(dp[0], nums[1]);for (int i = 2; i < len; ++i) {dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);}return Math.max(dp[len - 1], dp[len - 2]);}
}
👉👉方法2
(借鉴的方法)
step 1:用dp[i]表示长度为i的数组,最多能偷取到多少钱,只要每次转移状态逐渐累加就可以得到整个数组能偷取的钱。
step 2:(初始状态) 如果数组长度为1,只有一家人,因此dp[1]=nums[0]。
step 3:(状态转移) 每次对于一个人家,我们选择偷他或者不偷他,如果我们选择偷那么前一家必定不能偷,因此累加的上上级的最多收益,同理如果选择不偷他,那我们最多可以累加上一级的收益。因此转移方程为,dp[i]=max(dp[i−1],nums[i−1]+dp[i−2])。这里的i在dp中为数组长度,在nums中为下标。
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param nums int整型一维数组 * @return int整型*/public int rob (int[] nums) {//dp[i]表示长度为i的数组,最多能偷取多少钱int[] dp = new int[nums.length + 1];dp[1] = nums[0];for(int i = 2; i <= nums.length; i++)//对于每家可以选择不偷或者偷dp[i] = Math.max(dp[i - 1], nums[i - 1] + dp[i - 2]);return dp[nums.length];}
}
👉 注意点
在第一个方法中
这个是对的。
dp[1] = Math.max(dp[0], nums[1]);
这个是错的,通不过倒数第二个案例。
dp[1] = nums[1];
2. 打家劫舍(二)
题目来源:\textcolor{blue}{题目来源: }题目来源: BM79 打家劫舍(二)
等级:\textcolor{OrangeRed}{等级:}等级: 中等
👉题目描述
你是一个经验丰富的小偷,准备偷沿湖的一排房间,每个房间都存有一定的现金,为了防止被发现,你不能偷相邻的两家,即,如果偷了第一家,就不能再偷第二家,如果偷了第二家,那么就不能偷第一家和第三家。沿湖的房间组成一个闭合的圆形,即第一个房间和最后一个房间视为相邻。
给定一个长度为n的整数数组nums,数组中的元素表示每个房间存有的现金数额,请你计算在不被发现的前提下最多的偷窃金额。
数据范围:数组长度满足 1≤n≤2×1051≤n≤2×10^51≤n≤2×105 ,数组中每个值满足 1≤nums[i]≤50001≤nums[i]≤50001≤nums[i]≤5000
示例1
输入:[1,2,3,4]
返回值:6
说明:最优方案是偷第 2 4 个房间
示例2
输入:[1,3,6]
返回值:6
说明:由于 1 和 3 是相邻的,因此最优方案是偷第 3 个房间
👉代码编写
和上一题类似。但是本题中主要是有环形,意思就是选择第一家就不能选择最后一家,选择最后一家就不能选择第一家。那么我们就可以分类来讨论。
偷第一家,那么最后一家就不能偷
不偷第一家,那么意思就是dp[1]=0dp[1]=0dp[1]=0,去选择偷最后一家。
👉👉方法1
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param nums int整型一维数组 * @return int整型*/public int rob (int[] nums) {// write code hereint len = nums.length;if (len <= 1) return nums[0];int[] dp = new int[len + 1];dp[1] = nums[0];for (int i = 2; i < len; ++i) {dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]);}int result = dp[len - 1];Arrays.fill(dp, 0);dp[1] = 0;for (int i = 2; i <= len; ++i) {dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]);}return Math.max(dp[len], result);}
}
👉 注意点
注意环形,可以分开进行讨论。
3. 买卖股票的最好时机(一)
题目来源:\textcolor{blue}{题目来源: }题目来源: BM80 买卖股票的最好时机(一)
等级:简单\textcolor{OrangeRed}{等级:简单}等级:简单
👉题目描述
假设你有一个数组prices,长度为n,其中prices[i]是股票在第i天的价格,请根据这个价格数组,返回买卖股票能获得的最大收益
1.你可以买入一次股票和卖出一次股票,并非每天都可以买入或卖出一次,总共只能买入和卖出一次,且买入必须在卖出的前面的某一天
2.如果不能获取到任何利润,请返回0
3.假设买入卖出均无手续费
数据范围: 0≤n≤1050≤n≤10^50≤n≤105 , 0≤val≤1040≤val≤10^40≤val≤104
要求:空间复杂度 O(1),时间复杂度 O(n)
示例1
输入:[8,9,2,5,4,7,1]
返回值:5
说明:在第3天(股票价格 = 2)的时候买入,在第6天(股票价格 = 7)的时候卖出,最大利润 = 7-2 = 5 ,不能选择在第2天买入,第3天卖出,这样就亏损7了;同时,你也不能在买入前卖出股票。
示例2
输入:[2,4,1]
返回值:2
示例3
输入:[3,2,1]
返回值:0
👉代码编写
-
状态定义:
dp[i][j]:下标为 i 这一天结束的时候,手上持股状态为 j 时,我们持有的现金数。
j = 0,表示当前不持股; j = 1,表示当前持股。
dp[i][0]:第 i 天不持股到该天最大收益
dp[i][1]:第 i 天持股到该天最大收益 -
推导状态转移方程:
- dp[i][0]:当天不持股,有以下两种情况:
昨天不持股,今天什么都不做;
昨天持股,今天卖出股票(现金数增加),
状态转移方程:dp[i][0]=Math.max(dp[i−1][0],dp[i−1][1]+prices[i])dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i])dp[i][0]=Math.max(dp[i−1][0],dp[i−1][1]+prices[i]); - dp[i][1]:当天持股,有以下两种情况:
昨天持股,今天什么都不做(现金数与昨天一样);
昨天不持股,今天买入股票(注意:只允许交易一次,因此手上的现金数就是当天的股价的相反数)
状态转移方程:dp[i][1]=Math.max(dp[i−1][1],−prices[i])dp[i][1] = Math.max(dp[i - 1][1], -prices[i])dp[i][1]=Math.max(dp[i−1][1],−prices[i]);
- dp[i][0]:当天不持股,有以下两种情况:
👉👉方法1
import java.util.*;public class Solution {/*** * @param prices int整型一维数组 * @return int整型*/public int maxProfit (int[] prices) {// write code hereint n = prices.length;int[][] dp = new int[n][2];// 不持股dp[0][0] = 0;// 持股dp[0][1] = -prices[0];for (int i = 1; i < n; ++i) {// 什么都不做 / 持股卖出股票dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);// 继续持股 / 之前没有持股,买入股票dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);}return dp[n - 1][0];}
}
👉 注意点
虽然是个简单题,但是还是需要思考一下,状态方程和转移方程是如何。
4. 买卖股票的最好时机(二)
题目来源:\textcolor{blue}{题目来源: }题目来源:BM81 买卖股票的最好时机(二)
等级:中等\textcolor{OrangeRed}{等级:中等}等级:中等
👉题目描述
假设你有一个数组prices,长度为n,其中prices[i]是某只股票在第i天的价格,请根据这个价格数组,返回买卖股票能获得的最大收益
- 你可以多次买卖该只股票,但是再次购买前必须卖出之前的股票
- 如果不能获取收益,请返回0
- 假设买入卖出均无手续费
数据范围: 1≤n≤1×1051≤n≤1×10^51≤n≤1×105 , 1≤prices[i]≤1041≤prices[i]≤10^41≤prices[i]≤104
要求:空间复杂度 O(n),时间复杂度 O(n)
进阶:空间复杂度 O(1),时间复杂度 O(n)
示例1
输入:[8,9,2,5,4,7,1]
返回值:7
说明:
在第1天(股票价格=8)买入,第2天(股票价格=9)卖出,获利9-8=1
在第3天(股票价格=2)买入,第4天(股票价格=5)卖出,获利5-2=3
在第5天(股票价格=4)买入,第6天(股票价格=7)卖出,获利7-4=3
总获利1+3+3=7,返回7
示例2
输入:[5,4,3,2,1]
返回值:0
说明:由于每天股票都在跌,因此不进行任何交易最优。最大收益为0。
示例3
输入:[1,2,3,4,5]
返回值:4
说明:第一天买进,最后一天卖出最优。中间的当天买进当天卖出不影响最终结果。最大收益为4。
备注:
总天数不大于200000。保证股票每一天的价格在[1,100]范围内。
👉代码编写
和上一题类似,不过该题不需要控制购买次数。
- 状态定义:
dp[i][i]:下标为 i 这一天结束的时候,手上持股状态为 j 时,我们持有的现金数。
j = 0,表示当前不持股; j = 1,表示当前持股。
dp[i][0]:第 i 天不持股到该天最大收益
dp[i][1]:第 i 天持股到该天最大收益 - 状态转移:
- dp[i][0]: 当天不持股,表示前面卖了或者没有买。或者当天将股票卖出了。
状态转移方程dp[i][0]=Math.max(dp[i−1][0],dp[i−1][1]+price[i])dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + price[i])dp[i][0]=Math.max(dp[i−1][0],dp[i−1][1]+price[i])。 - dp[i][1]:当天持股,表示前面买入的股票还没有卖。或者当天买入了股票。
状态转移方程dp[i][1]=Math.max(dp[i−1][1],dp[i−1][0]−price[i])dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - price[i])dp[i][1]=Math.max(dp[i−1][1],dp[i−1][0]−price[i])
- dp[i][0]: 当天不持股,表示前面卖了或者没有买。或者当天将股票卖出了。
👉👉方法1
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可* 计算最大收益* @param prices int整型一维数组 股票每一天的价格* @return int整型*/public int maxProfit (int[] prices) {// write code hereint n = prices.length;int[][] dp = new int[n][2];dp[0][0] = 0;dp[0][1] = -prices[0];for (int i = 1; i < n; ++i) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);}return dp[n - 1][0];}
}
总结归纳
前方仍需努力。关于买卖股票这一个题还有一个困难题型,这里没有提出,有需求的小伙伴可以自行千万解决BM82 买卖股票的最好时机(三)。这一个题和(一)是类似的,但是加入了条件,只能进行两次购买票操作。
相关文章:
)
在动态规划的海洋中遨游(三)
前言:\textcolor{Green}{前言:}前言: 💞 好久没写题,有点生疏了。这也是给大家提一个醒,一定要一直坚持下去,哪怕每天只做一点点。💞 算法类别一、算法介绍原理适用的情况做题步骤二…...

enable_if模板编程实现字节序转换模板
enable_if和SFINAESFINAE是模板的一个特性,也就是替换失败不报错。正常来说,函数匹配的时候按照优先级依次匹配定义的重载函数,最终选择最佳匹配的函数运行。模板也是一样的,但是在替换模板时,即使出现异常错误也不认为…...

【人工智能与深度学习】基于能量的模型
【人工智能与深度学习】基于能量的模型 概述能量基础模型(EBM)方法定义解决方案:基于梯度的推理有潜在变量的能量基础模型推理例子能量基础模型和机率模型的对比自由能(Free Energy)概述 我们现在介绍一个新框架来定义模型。它提供了一个统一和系列性的方式来定义「监督模型」…...
功能测试三年,是应该改变了
前言 测试行业3年多经验,学历大专自考本科,主要测试方向web,PC端,wap站,小程序公众号都测试过,app也测过一些,C端B端都有,除功能外,接口性能也有涉猎,但是不…...
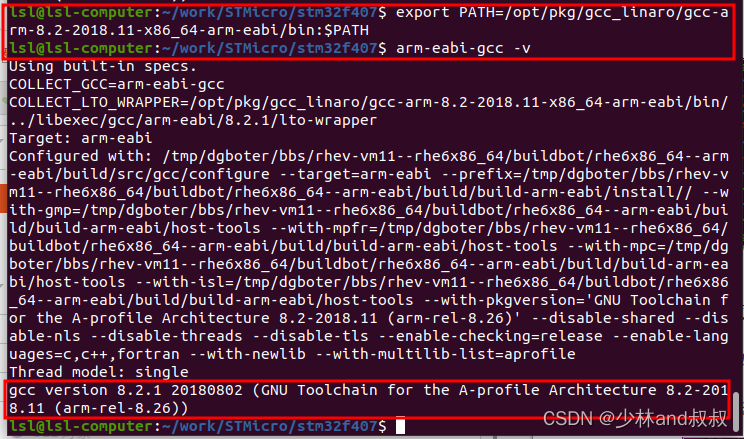
基于STM32的ubuntu交叉编译环境的搭建(arm-gcc 8.2)
常用的STM32的软件开发方法都是基于MDK keil或IAR集成开发环境,但以上两个集成开发环境软件都是需要收费的,且价格较为昂贵。本节介绍一种在ubuntu上安装arm gcc(arm-eabi)的方式,用于编译STM32的程序。 1.在arm官网下…...

数据结构:二叉树概念篇(算法基础)
目录 一.有向树的图论基础 1.有向树的相关基本概念 有向树的基本定义: 有向树的结点的度: 有向树的度: 有向树的根结点,分枝结点,叶结点: 树的子树: 树结点的层次: 树的高度: 2.一个基本的数学结论 3.有序有向树 二.数据结构中树的顺序存储结构与链式存…...

华为OD机试真题Java实现【字符串变换最小字符串】真题+解题思路+代码(20222
字符串变换最小字符串 给定一个字符串s,最多只能进行一次变换,返回变换后能得到的最小字符串(按照字典序进行比较)。 变换规则:交换字符串中任意两个不同位置的字符。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Java)真题目录汇总 ## 输入输出描述: …...

数字化转型的企业会用低代码平台深化重塑什么形态
随着数字化转型的浪潮不断推进,越来越多的企业开始关注如何更好地利用数字技术提高业务效率和创新能力。而低代码平台作为一种能够快速构建和部署应用程序的新型工具,正越来越受到企业的青睐。那么,数字化转型的企业会用低代码平台深化重塑什…...

【华为OD机试模拟题】用 C++ 实现 - 拼接 URL(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

六千字让你明白什么是数字孪生?
文章目录1. 背景2. 数字孪生基础2.1 概念2.2 价值3. 技术生态3.1 技术体系3.2 核心技术3.2.1 多领域、多尺度融合建模3.2.2 数据驱动与物理模型融合的状态评估3.2.3 数据采集和传输3.2.4 全生命周期数据管理3.2.5 虚拟现实呈现3.2.6 高性能计算3.3 建设3.3.1 重点3.3.1.1 数字孪…...
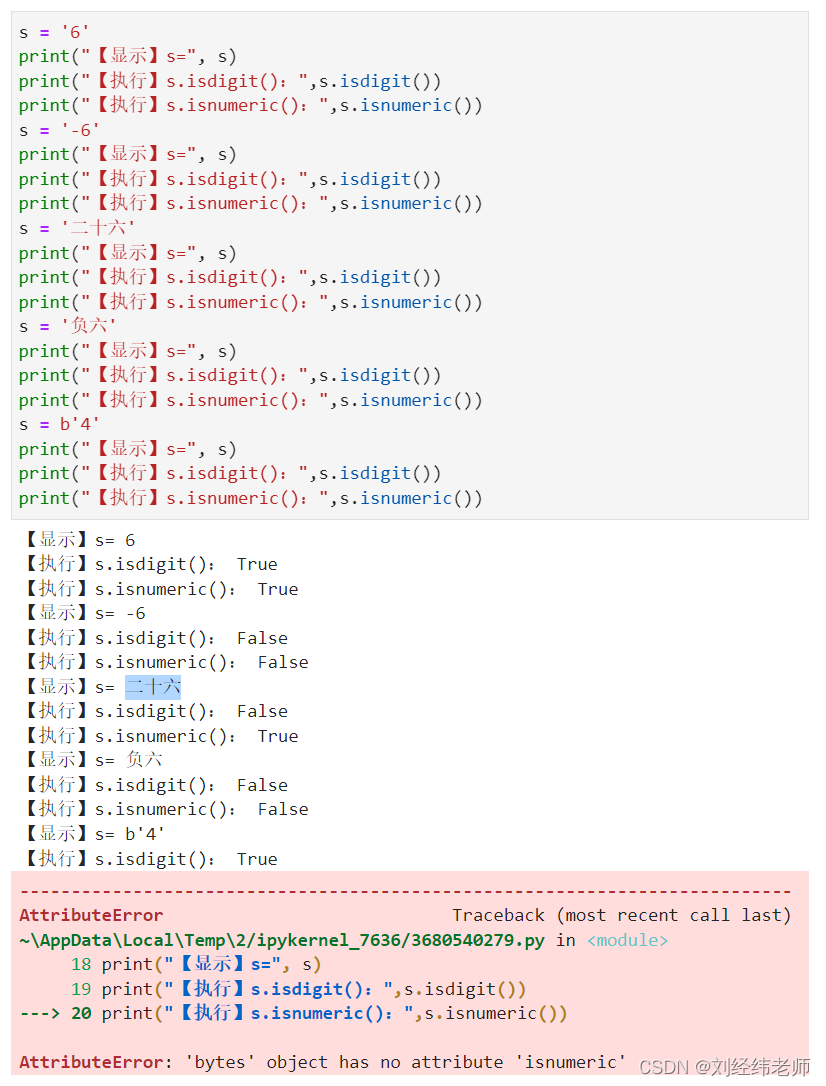
判断字符串是否是纯数字不包括符号(含符号显示False)isnumeric()和isdigit()
【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 判断字符串是否是纯数字 不包括符号(含符号显示False) isnumeric()和isdigit() [太阳]选择题 对于代码中当s为‘二十六’时isdigit()和isnumeric()输出的结果是? s …...

计算机408考研先导课---C语言难点2
目录 一、字符型数据与字符串型数据的比较 1、字符型数据特点 2、字符串型数据特点 二、字符数组 1、定义 2、输入输出 ①输入 ②输出 3、字符处理函数 ①put函数 ②gets函数 ③strcat函数 ④strcpy函数 ⑤strcmp函数 ⑥strlen函数 ⑦strlwr函数 ⑧strup…...

682. 棒球比赛
题目:你现在是一场采用特殊赛制棒球比赛的记录员。这场比赛由若干回合组成,过去几回合的得分可能会影响以后几回合的得分。 比赛开始时,记录是空白的。你会得到一个记录操作的字符串列表 ops,其中 ops[i] 是你需要记录的第 i 项操…...

【《C Primer Plus》读书笔记】第13章:文件输入/输出
【《C Primer Plus》读书笔记】第13章:文件输入/输出13.1 与文件进行通信13.1.1 文件是什么13.1.2 文本模式和二进制模式13.1.3 I/O的级别13.1.4 标准文件13.2 标准I/O13.3 一个简单的文件压缩程序13.4 文件I/O:fprintf()、fscanf()、fgets()和fputs()13…...
Datacom-HCIE考试经验分享
我是誉天Datacom秦同学。作为誉天众多通过Datacom-HCIE考试的学员之一,我感到很荣幸。 首先说说自学的感受吧: 我是从2020年开始接触网络行业的,听单位的前辈说华为的HCIE认证是行业含金量最高的证书,从那时起心里就种下了一个“I…...

第十二章 系统错误消息 - 一般系统错误消息 P - S
文章目录第十二章 系统错误消息 - 一般系统错误消息 P - S第十二章 系统错误消息 - 一般系统错误消息 P - S 错误代码描述<PARAMETER>由用户编写的函数引用或 Do 命令传递给标记行的参数数量超过了为标记行声明的形式参数的数量。<PRIVATE METHOD>已尝试调用一个私…...
【git】Idea中git的使用
配置git 创建git仓库 不同颜色代表的含义 红色——未加入版本控制;绿色——已经加入控制暂未提交;蓝色——加入,已提交,有改动;白色——加入,已提交,无改动;灰色——版本控制已忽略文…...
Centos安装Python、PyCharm
安装Python 1、打开终端(Terminal) 2、输入以下命令更新系统: sudo yum update 3、安装Python: sudo yum install python3 4、安装完成后,可以使用以下命令检查Python版本: python3 --version 安装PyCharm 1、下载PyCharm的安…...

搞百亿补贴,京东不能只“砸钱”
出品 | 何玺 排版 | 叶媛 京东“百亿补贴”真的要来了。 据多家媒体报道,京东“百亿补贴”已于2月23日启动内测。根据此前消息,京东“百亿补贴”频道将于3日晚8点正式上线。 在京东“百亿补贴”频道正式上线之前,我们来聊一聊“刘强东为什…...

automl介绍以及代码实例
使用AutoML来自动构建机器学习模型,可以使用多种不同的Python包,包括AutoGluon、TPOT、Auto-Keras等。AutoGluon可以自动搜索最佳模型,以便满足开发人员的需求;TPOT可以自动调整模型的参数,以获得更好的性能࿱…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
