数据结构:二叉树概念篇(算法基础)
目录
一.有向树的图论基础
1.有向树的相关基本概念
有向树的基本定义:
有向树的结点的度:
有向树的度:
有向树的根结点,分枝结点,叶结点:
树的子树:
树结点的层次:
树的高度:
2.一个基本的数学结论
3.有序有向树
二.数据结构中树的顺序存储结构与链式存储结构
1.数据结构的物理结构与逻辑结构
2.物理结构为顺序表(数组)的树形数据结构
3. 物理结构为链表的树形数据结构
三.二叉树
1.二叉树基本概念
2.两个重要的特殊二叉树
3. 关于二叉树的一些常用数学结论
(1).第一组结论
(2).第二组结论(数组实现二叉树的算法基础)
一.有向树的图论基础
基本引理:如果图G(结点数大于等于2)中不存在回路,则至少有一个结点的度为1。
本篇所讨论的树都是有向树
1.有向树的相关基本概念
有向树的基本定义:
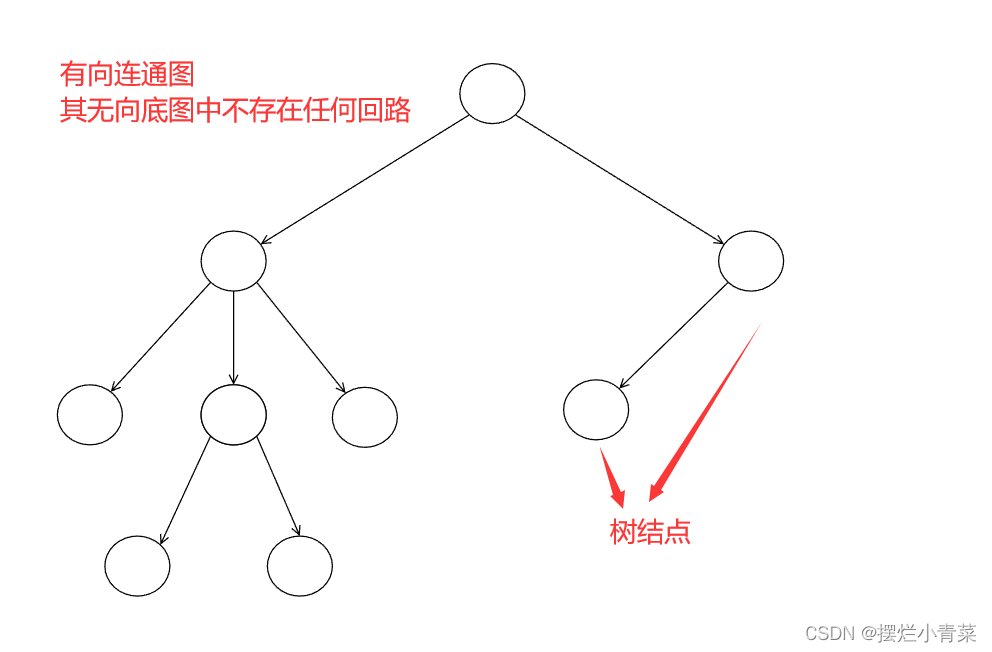
设T是由有限个结点构成的有向简单连通图,且T的无向底图中不存在任何回路,则称T为有向树:
有向树的结点的度:
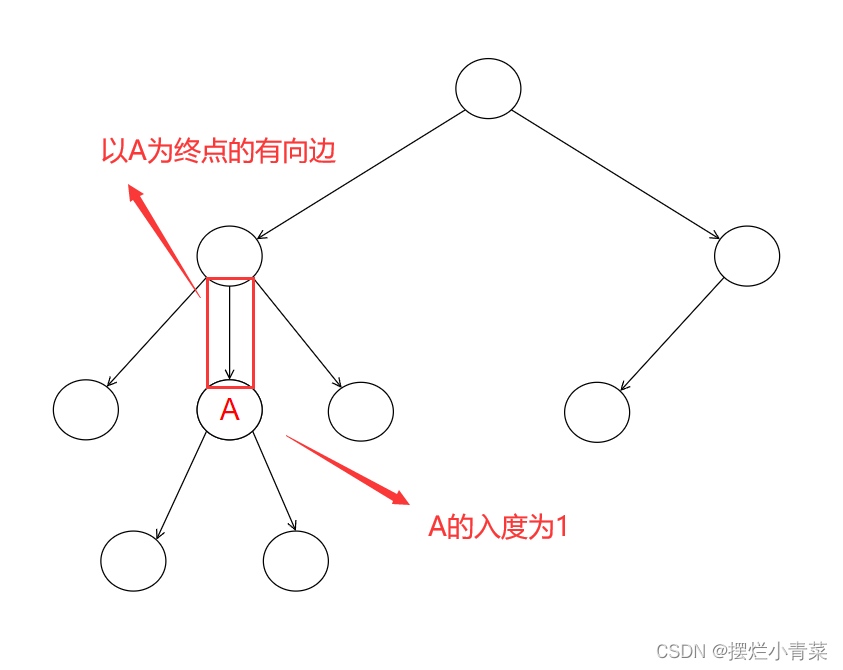
结点的入度:现有树结点A,以A为终点的有向边的条数称为结点A的入度:
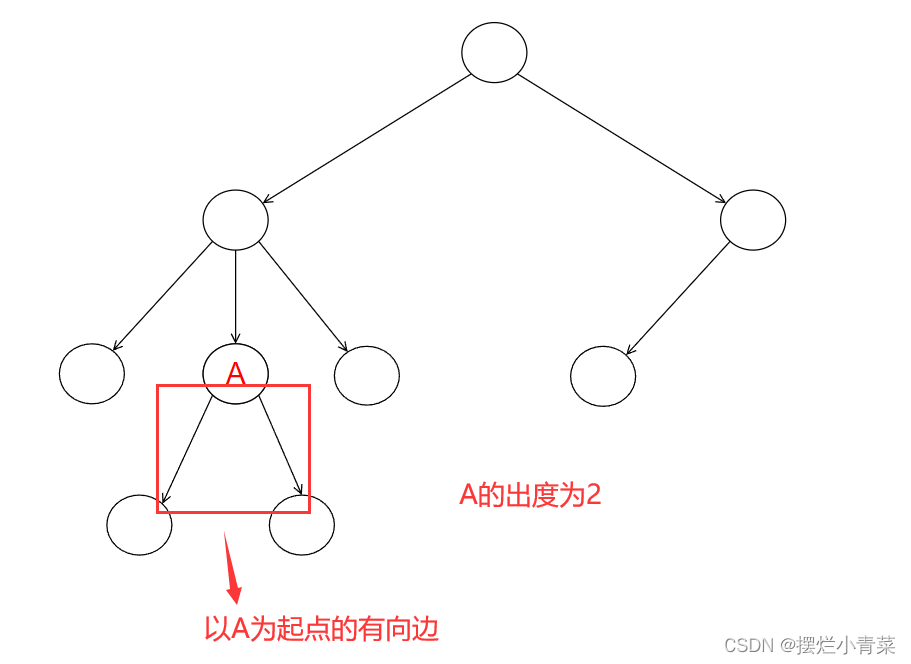
结点的出度: 现有树结点A,以A为起点的有向边的条数称为结点A的出度:
以结点A为终点的有向边的另一端的结点称为A的父结点(parent)
以结点A为起点的有向边的另一端的结点称为A的孩子结点(child)
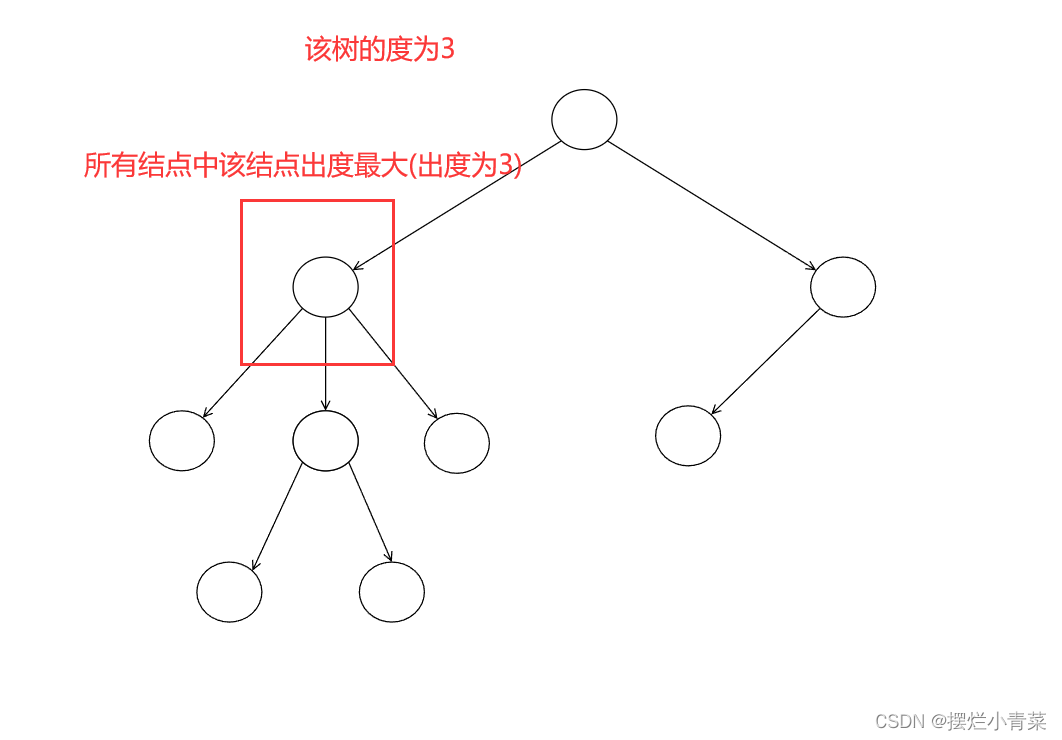
有向树的度:
有向树的度 = 该树所有结点的出度中的最大值:
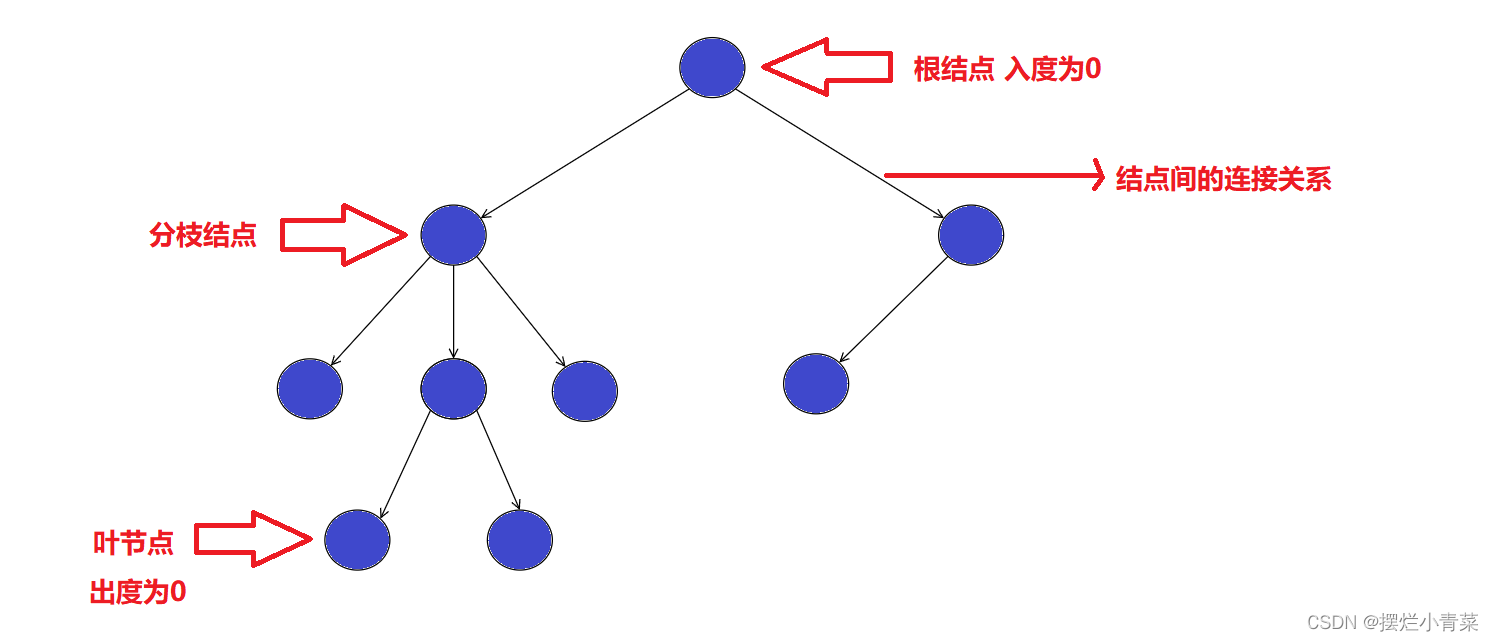
有向树的根结点,分枝结点,叶结点:
- 根结点的入度为0
- 叶结点的出度为0
- 其余入度和出度均不为0的结点称为树的分枝结点
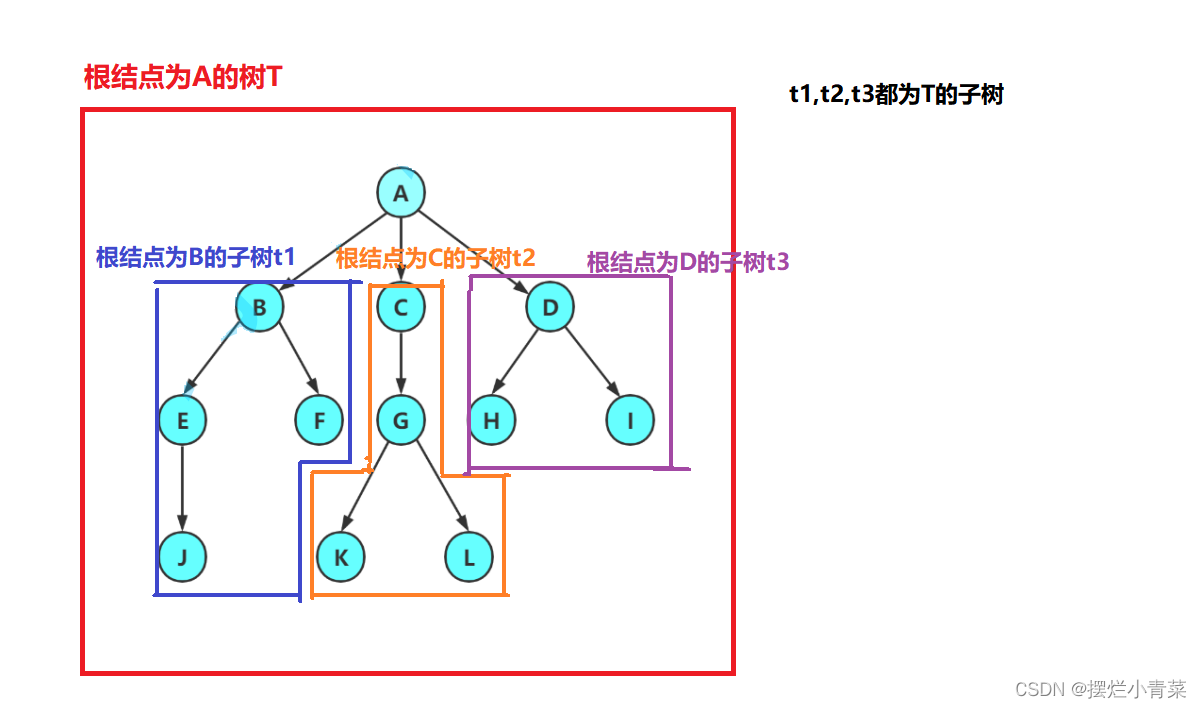
树的子树:
将一个有向树T的根结点去掉,该树则会被分成若干个互不连通的子树,如图:
上图中T的子树t1,t2,t3都可以再以相同的方式被划分成更小的子树直到树图被划分为若干树叶.
注意:在仅有一个根结点的树形结构中,子树之间没有通路(不然图中会出现回路)
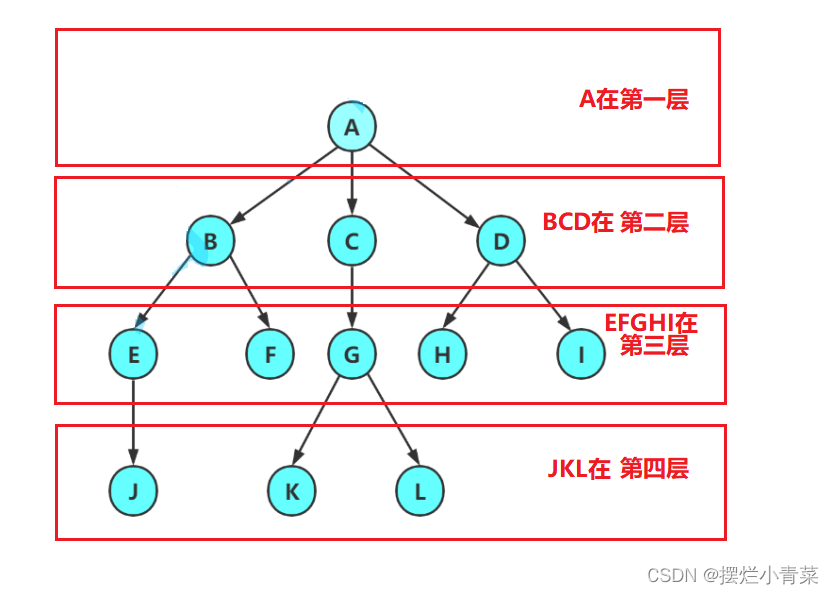
树结点的层次:
从根结点开始算起,沿着有向边进行遍历,从根结点到某一个特定结点所遍历的结点个数称为某特定结点的层次
- 层次相同且父结点相同的结点互为兄弟结点(比如上图中的E和F)
- 层次相同但父结点不同的结点互为堂兄弟结点(比如上图中的F和G)
树的高度:
树的所有结点的层次中的最大值称为该树的高度:比如上图中的树的高度为4
2.一个基本的数学结论
- 关于树的一个基本命题:若树有n个结点,m条有向边,则m=n-1;
该性质可以通过数学归纳法进行证明:
- 显然n=1时,则m=0,m=n-1成立;
- 假设n=k(k>=1)时命题成立,即任意具有k个结点的树都有k-1条边。
- 设树G有n=k+1个结点时(k>=1),边数为m。 由于G中没有回路,根据基本引理G中必然存在度(出度+入度)为1的结点,设这个结点为u。 从G中删去结点u(相当于同时删去了一条边和一个结点),根据定义G仍是树,(根据n=k时的假设2)G有k个节点,故有k-1条边,从而m=(k-1)+1=k=n-1(将u结点加回来,边数相应地增加1)。(即若n=k时命题成立则n=k+1时命题也成立,那么从n=1开始构建任意结点数量的树也满足m=n-1)
该证明过程充分体现了树在逻辑上是递推构建起来的图:
分析树的构建图解可知:
- 若构建仅有一个根结点的有向树,则该有向树的每棵子树的根结点有且只有一个父节点,可以有0个或多个孩子结点.
- 同时易知:在仅有一个根结点的树形结构中,一棵树的子树之间不存在通路
3.有序有向树
满树的概念:
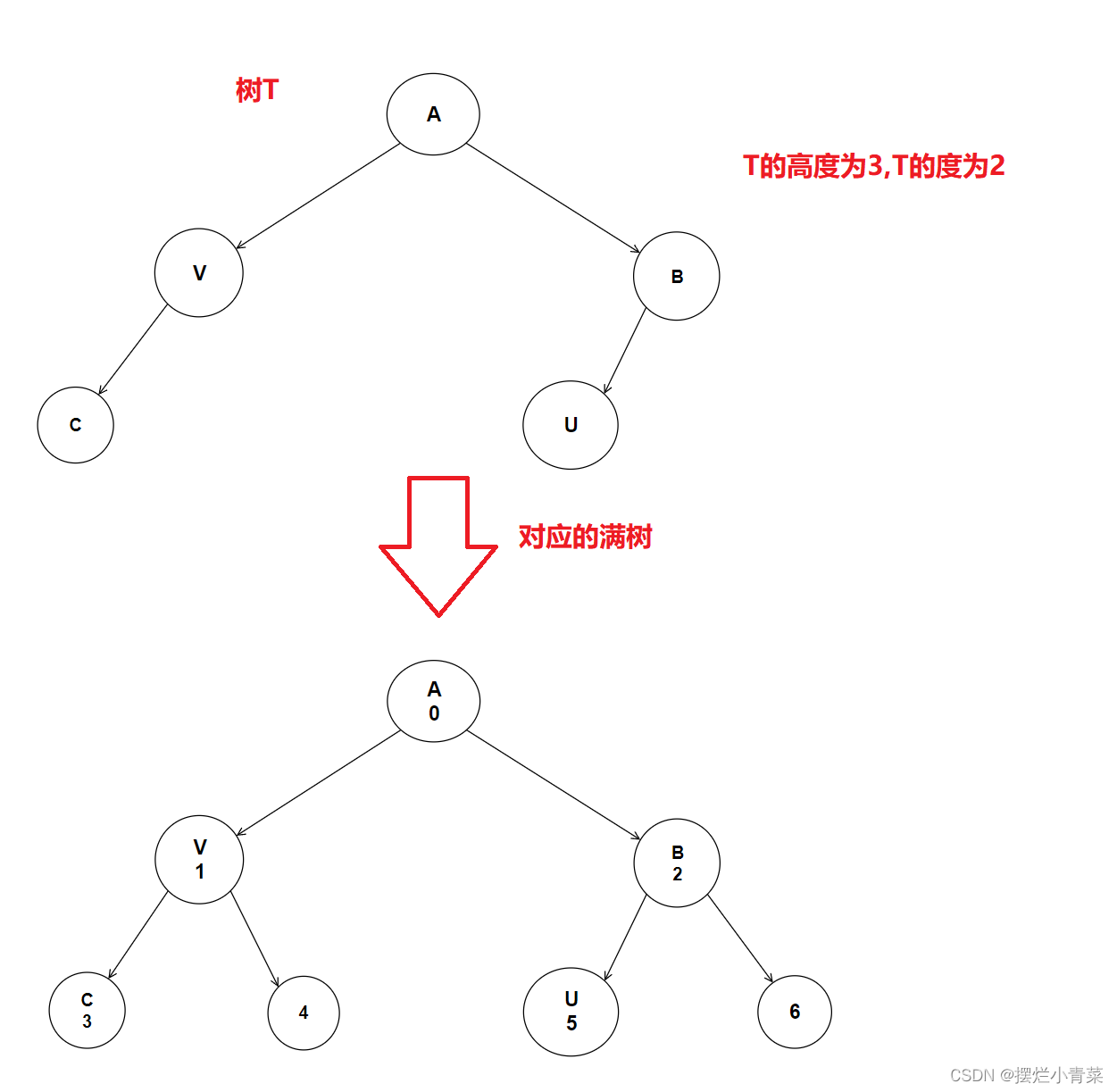
- 设(单个根结点)树T的高度为h(h>1),度为k(k>=1)(树的结点个数大于1)
- 树T对应的满树的概念:高度为h且根结点和每一个分枝结点的出度都为k的树。
- 有序有向树的每一个结点都有自己固定的编号
有序有向树各结点的编号规则:
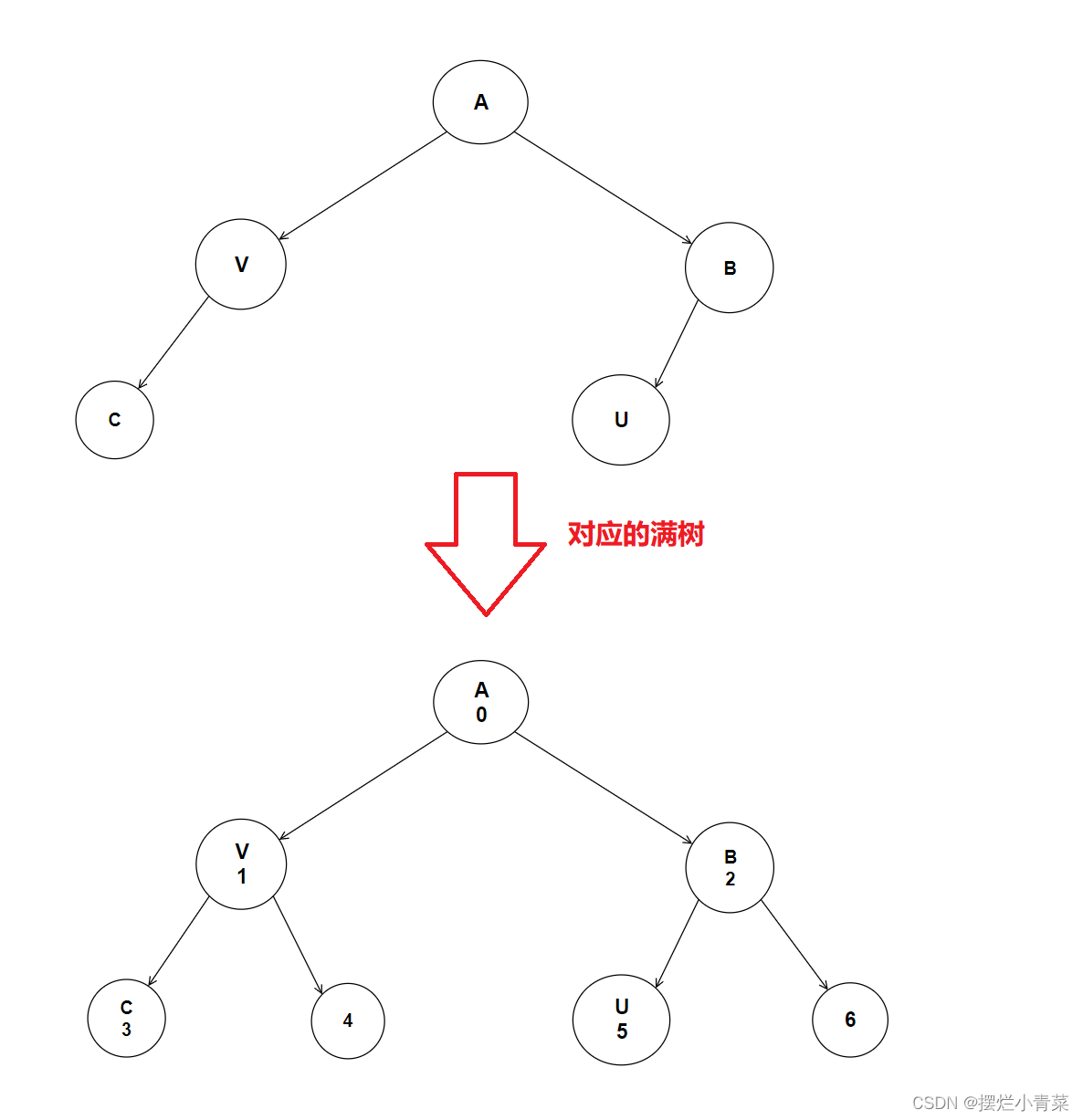
- 设现在有一颗高度为h,度为k的(单个根结点的)树T(h>1,,k>=1)
- 先作出树T对应的满树
- 将树T对应的满树的各结点按照从低层到高层,从左往右的次序进行编号
- 根据满树各结点的编号对树T相应位置的结点进行编号
比如:
二.数据结构中树的顺序存储结构与链式存储结构
如果将树的结点看成是一个个内存区块,结点间的有向线段看成是各内存区块之间的关联(这种关联可能是通过指针或者数组下标关系建立起来的),这种在内存中形成的数据结构就是树形数据结构
1.数据结构的物理结构与逻辑结构
- 数据结构的物理结构指的是该数据结构在内存中的真实分布模型
- 数据结构的逻辑结构指的是数据结构的抽象分析模型
数据结构的类型主要取决于其逻辑结构,其逻辑结构和物理结构之间是通过逻辑映射来建立联系的。
2.物理结构为顺序表(数组)的树形数据结构
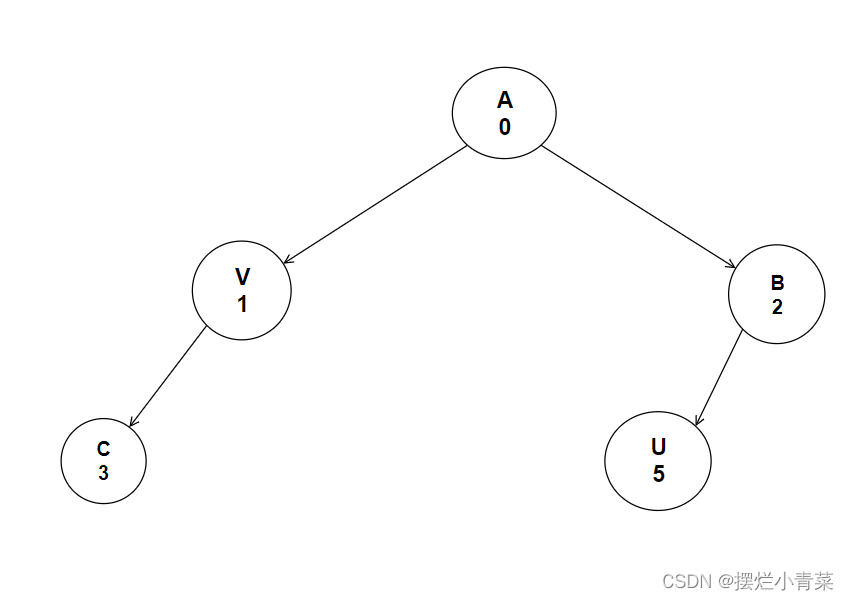
- 现有一颗度数为2的非满树T
- 我们先将一个树T对应的满树的各个结点按照从低层次到高层次,从左往右的顺序进行编号:
- 由此我们可以得到树T各个结点的编号:
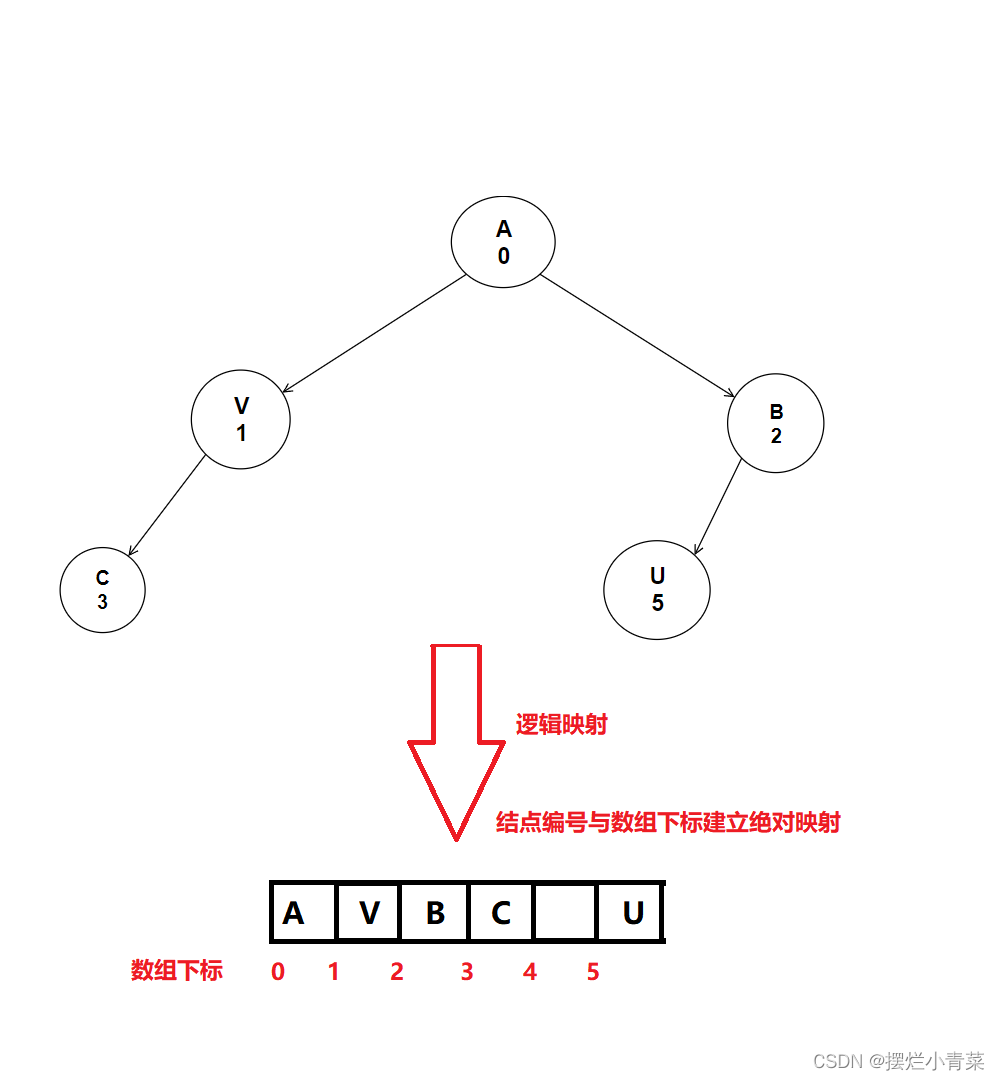
- 根据树T各结点的编号我们就可以将这棵树映射到一个数组上去:
- 通过结点编号与数组下标的绝对映射,我们便可以通过数组来实现树形数据结构(有序有向树)
- 顺序表实现的树中,非常经典的例子就是堆(大小根堆)
3. 物理结构为链表的树形数据结构
我们可以定义一个结构体类型:
typedef int DataType; struct Node {struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域 };
- _firstChild1用于指向该结点的第一个孩子结点(编号意义上的第一个(位于左侧))
- _pNextBrother用于指向与该结点位于相同层次且具有相同父结点的兄弟结点
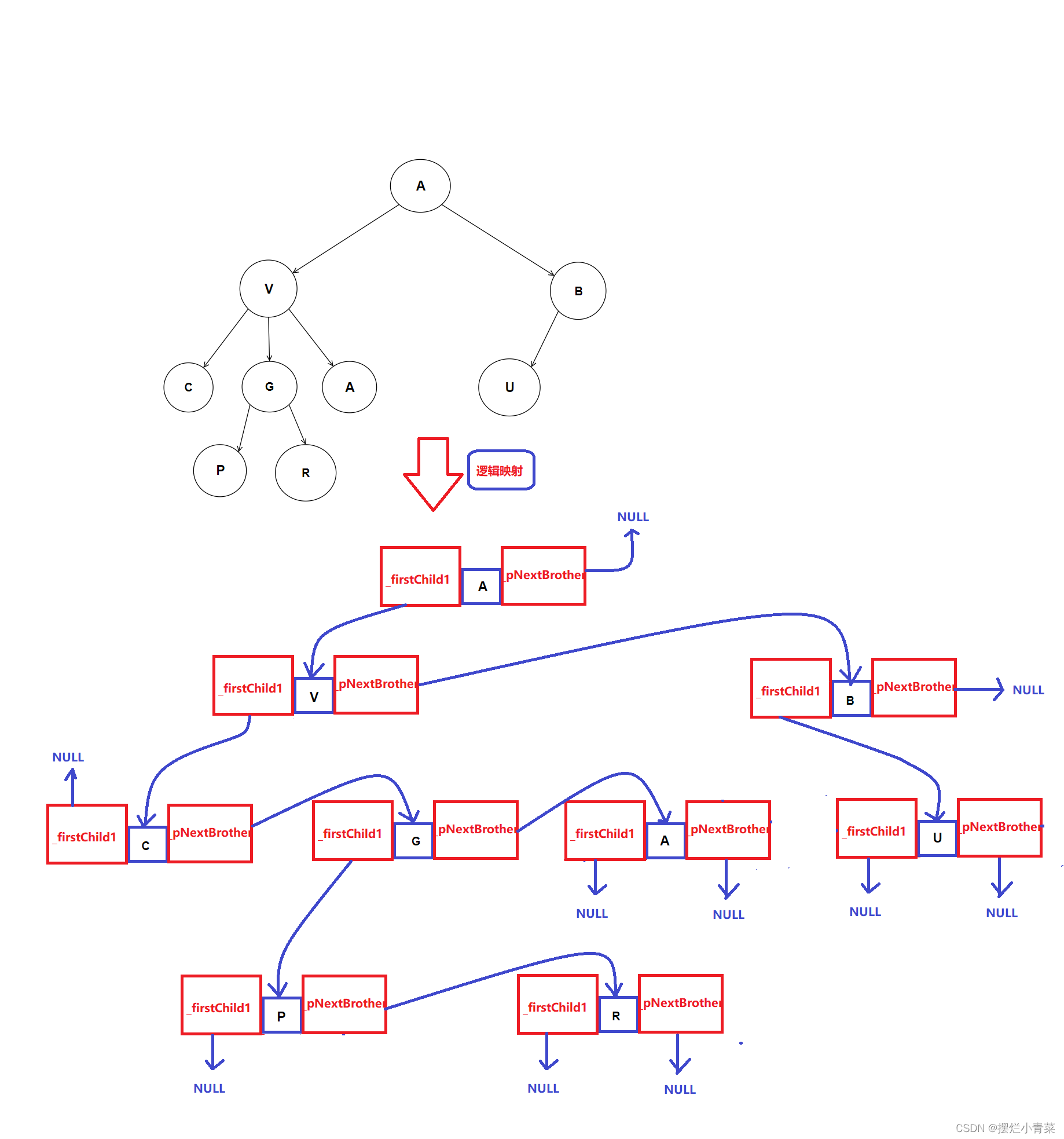
现在有一颗树:
我们用链式存储结构来实现它:
通过_firstChild1指针我们可以实现树的深度遍历
通过_pNextBrother指针我们可以实现树的广度遍历
三.二叉树
1.二叉树基本概念
一棵二叉树是结点的一个有限集合:
- 二叉树的度为2,即不存在出度大于2的结点
- 二叉树结点的孩子结点有左右之分(左右孩子),次序不能颠倒,二叉树是有序有向树(各结点都有自己对应的固定编号)
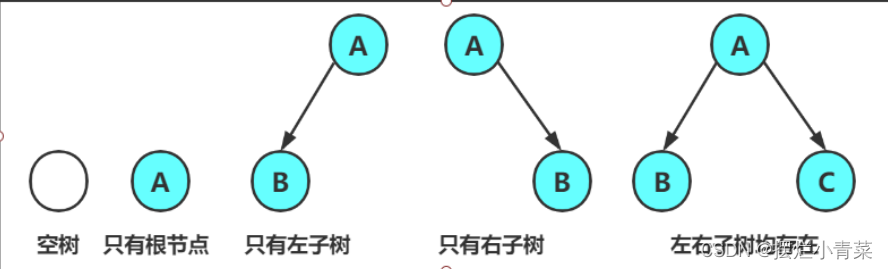
对于任意的二叉树都是由以下几种情况复合而成的
2.两个重要的特殊二叉树
- 满二叉树:一个二叉树,如果根结点和每一个分枝结点的出度都为2,则这个二叉树就是满二叉树。从结点总个数角度分析:如果一个二叉树的层数为K,且结点总数是2^k - 1(等比数列求和),则它就是满二叉树.
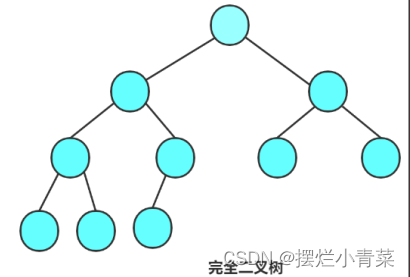
- 完全二叉树:完全二叉树是效率很高的数据结构;
对于高度为K的,有n个结点的二叉树,当且仅当其所有结点编号为1到n连续排列时称之为完全二叉树。(基于完全二叉树的结点编号特点,用数组来实现完全二叉树,内存利用率较高)完全二叉树有一个特点:
若完全二叉树的高度为k(k>1),则其前k-1层所有结点构成的子结构是一颗满树
- 用数组实现完全二叉树和非完全二叉树的对比:可见完全二叉树的优势所在
- 数据结构堆就是用顺序表(数组)实现的完全二叉树(堆是堆排序算法的结构基础)
3. 关于二叉树的一些常用数学结论
接下来我们给出两组在后续的算法学习中会用到的关于二叉树的数学结论
(1).第一组结论
- 对任何一棵二叉树, 如果出度为0其叶结点个数为N0, 出度为2的分支结点个数为N2(包括根) ,则有 N0= N2+1
证明:
设该二叉树出度为1的分枝结点个数为N1;
则该二叉树中的总边数为: 2*N2 + N1;
该二叉树中的总结点个数为: N0 + N1 + N2
根据第一章第2小节的基本数学结论有:2*N2 + N1 = N0 + N1 + N2 -1(树的总边数 = 结点数-1)
化简可得:N0 = N2 +1;(即二叉树中,出度为0的树叶永远比出度为2的分枝结点(包括根)多一个)
(2).第二组结论(数组实现二叉树的算法基础)
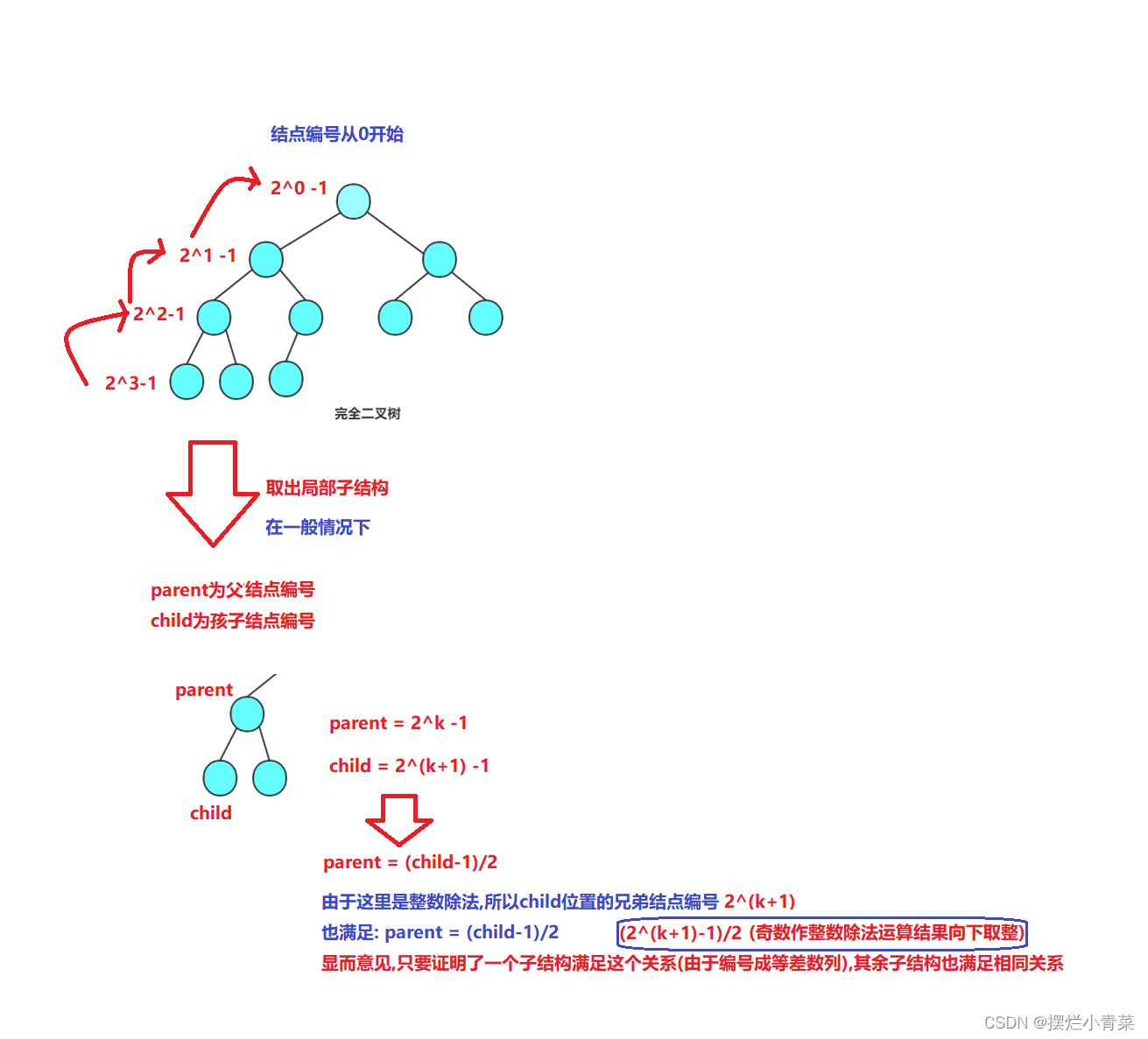
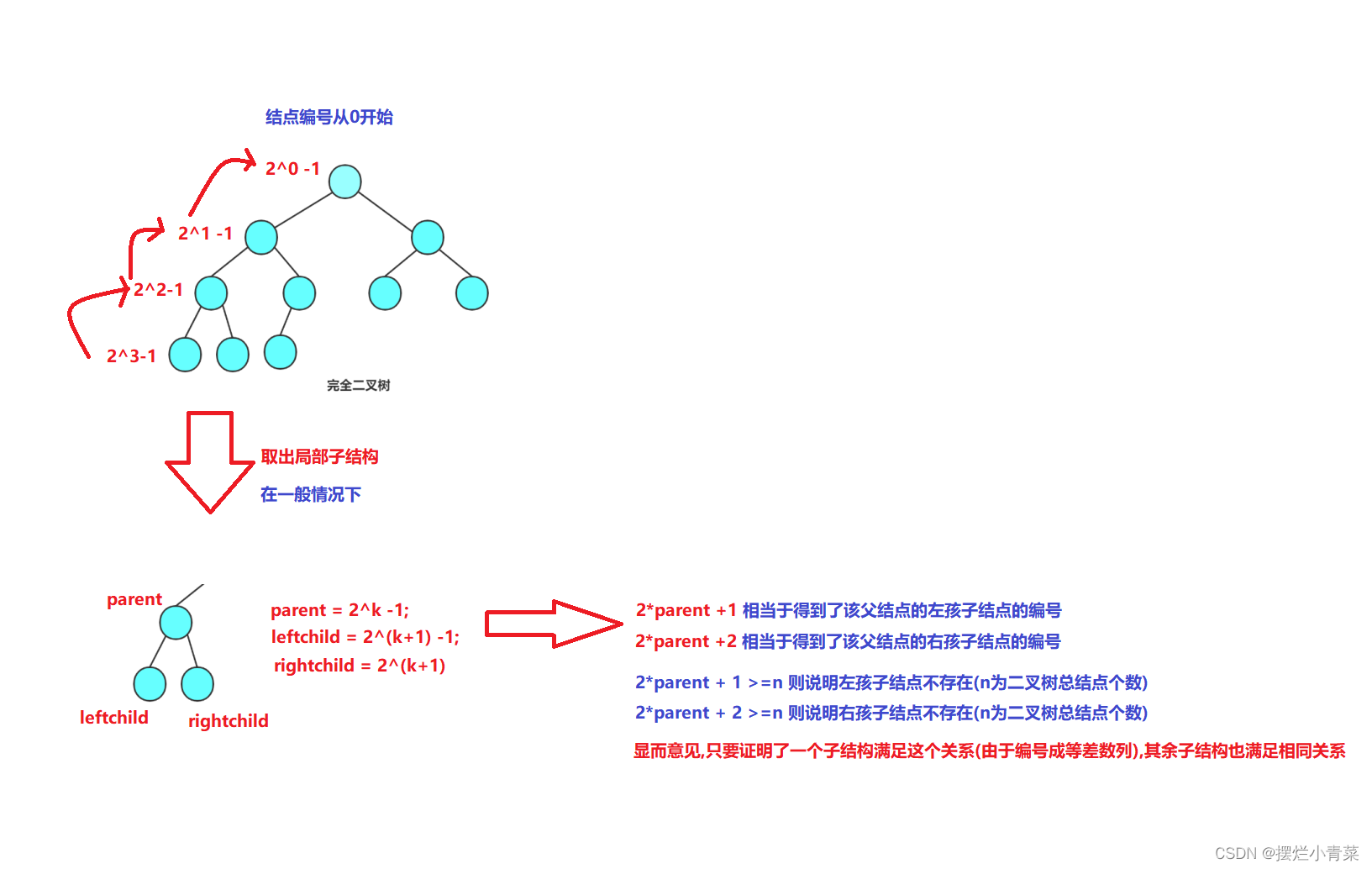
- 定理一:对于具有n个结点的完全二叉树,按照第一章第3节所述的编号规则将其各结点进行编号(根结点我们规定编为0号,则完全二叉树的各结点编号为0~n-1),则对于编号为child的结点有如下结论:若child>0,child编号结点的父结点编号parent = (child-1)/2;若child=0 ,该结点无父结点

定理一证明图解:
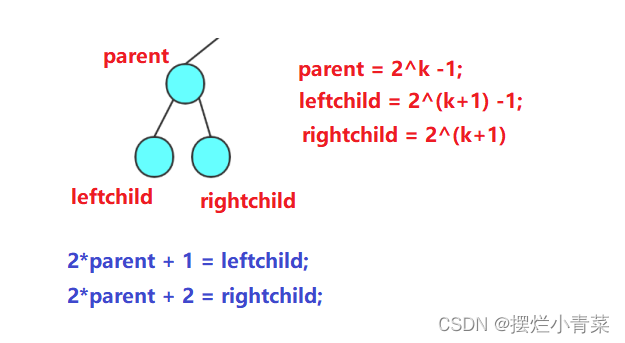
- 定理二:对于具有n个结点的完全二叉树,按照第一章第3节所述的编号规则将其各结点进行编号(根结点我们规定编为0号,则完全二叉树的各结点编号为0~n-1),则对于编号为parent的结点有如下结论:若2*parent+1<n,则可得该结点的左孩子结点编号leftchild = 2*parent+1;若2*parent+1>=n,则该结点无左孩子(该结论是定理一的逆定理)
- 定理三:对于具有n个结点的完全二叉树,按照第一章第3节所述的编号规则将其各结点进行编号(根结点我们规定编为0号,则完全二叉树的各结点编号为0~n-1),则对于编号为parent的结点有如下结论:若2*parent+2<n,则可得该结点的右孩子结点编号rightchild = 2*parent+2;若2*parent+2>=n则该结点无右孩子(该结论是定理一的逆定理)
定理二和三的证明分析图解:
有了该组定理我们就可以通过一个父结点的编号找到其左右孩子结点的编号,反过来也可以通过孩子结点的编号找到其父结点的编号(该组定理为数组实现二叉树奠定了算法基础)
- 该组定理在后续堆的实现中的堆元素插入删除接口的元素上下调整算法中会用到

相关文章:

数据结构:二叉树概念篇(算法基础)
目录 一.有向树的图论基础 1.有向树的相关基本概念 有向树的基本定义: 有向树的结点的度: 有向树的度: 有向树的根结点,分枝结点,叶结点: 树的子树: 树结点的层次: 树的高度: 2.一个基本的数学结论 3.有序有向树 二.数据结构中树的顺序存储结构与链式存…...

华为OD机试真题Java实现【字符串变换最小字符串】真题+解题思路+代码(20222
字符串变换最小字符串 给定一个字符串s,最多只能进行一次变换,返回变换后能得到的最小字符串(按照字典序进行比较)。 变换规则:交换字符串中任意两个不同位置的字符。 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Java)真题目录汇总 ## 输入输出描述: …...

数字化转型的企业会用低代码平台深化重塑什么形态
随着数字化转型的浪潮不断推进,越来越多的企业开始关注如何更好地利用数字技术提高业务效率和创新能力。而低代码平台作为一种能够快速构建和部署应用程序的新型工具,正越来越受到企业的青睐。那么,数字化转型的企业会用低代码平台深化重塑什…...

【华为OD机试模拟题】用 C++ 实现 - 拼接 URL(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

六千字让你明白什么是数字孪生?
文章目录1. 背景2. 数字孪生基础2.1 概念2.2 价值3. 技术生态3.1 技术体系3.2 核心技术3.2.1 多领域、多尺度融合建模3.2.2 数据驱动与物理模型融合的状态评估3.2.3 数据采集和传输3.2.4 全生命周期数据管理3.2.5 虚拟现实呈现3.2.6 高性能计算3.3 建设3.3.1 重点3.3.1.1 数字孪…...
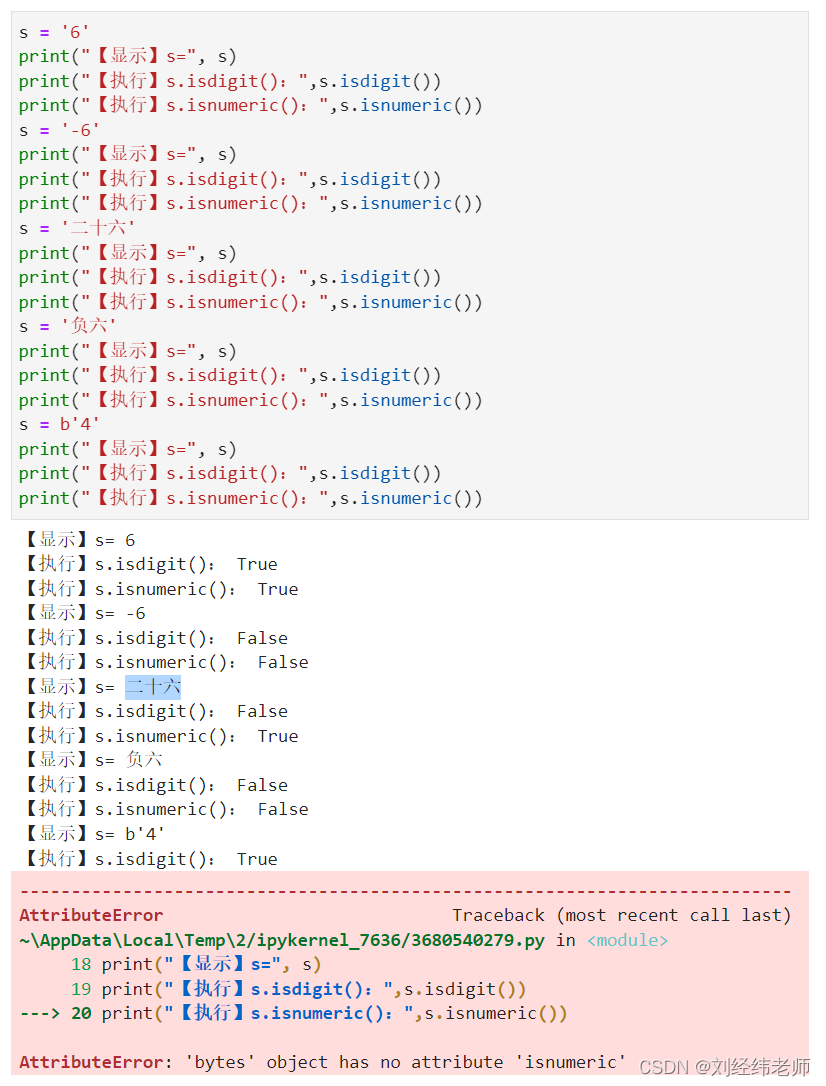
判断字符串是否是纯数字不包括符号(含符号显示False)isnumeric()和isdigit()
【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 判断字符串是否是纯数字 不包括符号(含符号显示False) isnumeric()和isdigit() [太阳]选择题 对于代码中当s为‘二十六’时isdigit()和isnumeric()输出的结果是? s …...

计算机408考研先导课---C语言难点2
目录 一、字符型数据与字符串型数据的比较 1、字符型数据特点 2、字符串型数据特点 二、字符数组 1、定义 2、输入输出 ①输入 ②输出 3、字符处理函数 ①put函数 ②gets函数 ③strcat函数 ④strcpy函数 ⑤strcmp函数 ⑥strlen函数 ⑦strlwr函数 ⑧strup…...

682. 棒球比赛
题目:你现在是一场采用特殊赛制棒球比赛的记录员。这场比赛由若干回合组成,过去几回合的得分可能会影响以后几回合的得分。 比赛开始时,记录是空白的。你会得到一个记录操作的字符串列表 ops,其中 ops[i] 是你需要记录的第 i 项操…...

【《C Primer Plus》读书笔记】第13章:文件输入/输出
【《C Primer Plus》读书笔记】第13章:文件输入/输出13.1 与文件进行通信13.1.1 文件是什么13.1.2 文本模式和二进制模式13.1.3 I/O的级别13.1.4 标准文件13.2 标准I/O13.3 一个简单的文件压缩程序13.4 文件I/O:fprintf()、fscanf()、fgets()和fputs()13…...
Datacom-HCIE考试经验分享
我是誉天Datacom秦同学。作为誉天众多通过Datacom-HCIE考试的学员之一,我感到很荣幸。 首先说说自学的感受吧: 我是从2020年开始接触网络行业的,听单位的前辈说华为的HCIE认证是行业含金量最高的证书,从那时起心里就种下了一个“I…...

第十二章 系统错误消息 - 一般系统错误消息 P - S
文章目录第十二章 系统错误消息 - 一般系统错误消息 P - S第十二章 系统错误消息 - 一般系统错误消息 P - S 错误代码描述<PARAMETER>由用户编写的函数引用或 Do 命令传递给标记行的参数数量超过了为标记行声明的形式参数的数量。<PRIVATE METHOD>已尝试调用一个私…...
【git】Idea中git的使用
配置git 创建git仓库 不同颜色代表的含义 红色——未加入版本控制;绿色——已经加入控制暂未提交;蓝色——加入,已提交,有改动;白色——加入,已提交,无改动;灰色——版本控制已忽略文…...
Centos安装Python、PyCharm
安装Python 1、打开终端(Terminal) 2、输入以下命令更新系统: sudo yum update 3、安装Python: sudo yum install python3 4、安装完成后,可以使用以下命令检查Python版本: python3 --version 安装PyCharm 1、下载PyCharm的安…...

搞百亿补贴,京东不能只“砸钱”
出品 | 何玺 排版 | 叶媛 京东“百亿补贴”真的要来了。 据多家媒体报道,京东“百亿补贴”已于2月23日启动内测。根据此前消息,京东“百亿补贴”频道将于3日晚8点正式上线。 在京东“百亿补贴”频道正式上线之前,我们来聊一聊“刘强东为什…...

automl介绍以及代码实例
使用AutoML来自动构建机器学习模型,可以使用多种不同的Python包,包括AutoGluon、TPOT、Auto-Keras等。AutoGluon可以自动搜索最佳模型,以便满足开发人员的需求;TPOT可以自动调整模型的参数,以获得更好的性能࿱…...

kill 与killall
【查询命令所属软件包】 rpm -qf /usr/bin/killall psmisc-22.20-15.el7.x86_64 rpm -qf /usr/bin/kill util-linux-2.23.2-65.el7_9.1.x86_64 【命令参数】 killallkill -e,--exact require exact match for very long names -I,--ignore-case case insensi…...

【加密】开发常见加密类型
相关加密方法具体使用,查阅工具官方; 对称加密(单密钥加密):常用于传输数据加密 信息的加密和解密使用相同密钥; 常见对称算法: DES(Data Encryption Standard)&#x…...
数据结构之基:从根儿上了解数据结构的特性
学好数据结构,就等于成功了一半。 程序是对现实的模拟,现实是由时间和空间组成的,高效的人都是用最少的时间、最少的空间来做最伟大的事,程序亦是如此。我们要选择最合理的算法和最合理的数据结构,来写最好的代码&…...

C++ 枚举详解
C 枚举详解 C 枚举类型详解 枚举类型的定义格式为: enum <类型名> {<枚举常量表>};关键字enum——指明其后的标识符是一个枚举类型的名字枚举常量表——由枚举常量构成。“枚举常量"或称"枚举成员”,是以标识符形式表示的整型量&…...

【vue3】ref , reactive ,toRef ,toRefs 使用和理解
这篇文章是基于理解写的,仅助于理解,如有任何错误之处,感谢指正! 文章目录一.ref的使用1. ref的功能主要有两个:2.使用ref注意事项二.reactive的使用三.使用ref 和 reactive 实现双向数据绑定四.toRef 和 toRefs 的使用…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...